Урок алгебры в 8 классе «Решение квадратных неравенств. Метод иртервалов»
 Скачать 29.76 Kb. Скачать 29.76 Kb.
|
| Урок алгебры в 8 классе «Решение квадратных неравенств.Метод иртервалов » Цели урока: 1) образовательная:
2)воспитательная:
3) развивающая:
Оборудование:
Тип урока: урок обобщения и систематизации знаний.  Ход урока.
1.Проверить готовность учащихся к уроку. 2. Ознакомить учащихся с целями и задачами урока.
1. Фронтальная работа : слайды 1-2 Слайд 1 Слайд 2 Далее давайте вспомним, как знак дискриминанта влияет на решение неравенства, выполним следующее задание: назовите число корней уравнения ах2 + bх + с = 0 и знак коэффициента а, если график соответствующей квадратичной функции расположен следующим образом Слайд 3. Назовите промежутки, на которых функции принимает положительные и отрицательные значения, если ее график расположен указанным образом (Слайд 4): Восстановите алгоритм решения квадратных неравенств из заготовленных фраз (Слайд 5): Определить знак одного из интервалов. Найти корни квадратного уравнения (если это возможно). Расставить поочередно знаки в интервалах. Схематично построить график данной функции. Записать ответ. 2Письменная работа Из таблицы 1 выберите одну графическую интерпретацию для каждого из неравенств 1- 4? При необходимости выполните необходимые вычисления. (Слайд 6) В таблице 2 найдите верное решение неравенства 1, в таблице 3 – решение неравенства 2. (Слайд 7) 1) На доске изображен квадрат с числами, которые являются решениями неравенства 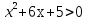 . Но среди них попало число, которое таковым не является. Найдите это число. . Но среди них попало число, которое таковым не является. Найдите это число.
Решение: 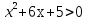 Квадратное уравнение   имеет два различных корня: имеет два различных корня: . Следовательно, квадратный трехчлен . Следовательно, квадратный трехчлен  можно представить в виде можно представить в виде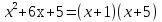 . Поэтому данное неравенство можно записать в виде . Поэтому данное неравенство можно записать в виде . Отсюда получаем две системы: . Отсюда получаем две системы: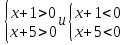  Решая первую систему, получим: Решая первую систему, получим:  Решая вторую систему, получим: 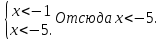 Так как х  2. 2.3. Самостоятельная работа (тест) Самостоятельная работа . Вариант 1 А1. Постройте график функции  . С помощью графика решите неравенство . С помощью графика решите неравенство 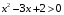 . .А2. Решите неравенство: 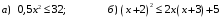 . .А3. Решите неравенство методом интервалов:  В1. Решите неравенство: 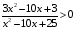 . .Вариант 2 А1. Постройте график функции  . С помощью графика решите неравенство . С помощью графика решите неравенство  А2. Решите неравенство: 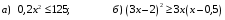 . .А3. Решите неравенство методом интервалов:  В1. Решите неравенство: 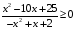 . . |