Ученица 6 «А» класса мбоу «сош №54». Редактор: учитель математики Бачурина Е. Г. г. Кемерово, 2015

Скачать 92.74 Kb. Название Ученица 6 «А» класса мбоу «сош №54». Редактор: учитель математики Бачурина Е. Г. г. Кемерово, 2015 Бачурина Е.Г Дата 16.02.2016 Размер 92.74 Kb. Тип Документы

Составитель: Филимонова Елизавета, ученица 6 «А» класса МБОУ «СОШ № 54». Редактор: учитель математики Бачурина Е.Г. г. Кемерово, 2015 Математика - зарядка для ума. ВВЕДЕНИЕ Каждый из нас хоть раз пробовал разгадывать кроссворды, ребусы, головоломки. В последнее время, наряду с буквенными кроссвордами, все чаще стали появляться кроссворды с числами. Числовые головоломки и кроссворды - это и приятное времяпровождение, и тренировка памяти, развитие логики и мышления. Особенно такие кроссворды полезны школьникам, ведь они могут потренироваться в устном счете и простых математических вычислениях. Всем известно, что устный счет по математике - один из самых действенных приемов развития интеллектуальных способностей. Умение считать в уме и оперировать цифрами ассоциируется с высоким интеллектом. Существует достаточное количество кроссвордов и головоломок из чисел, поэтому каждый желающий может выбрать кроссворд для себя. Желаем успехов! ЧИСЛОВОЙ КРОССВОРД Кроссворд, в котором вместо слов вписываются числа. Под сеткой указаны все числа из этого кроссворда в порядке возрастания. Найдите правильное месторасположение для каждого числа. 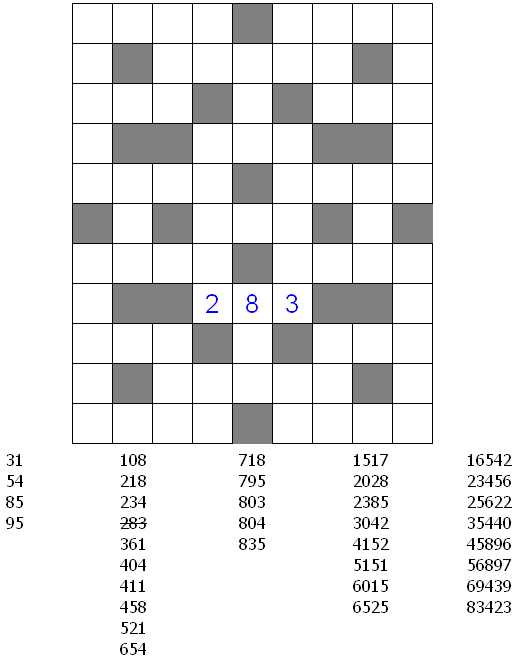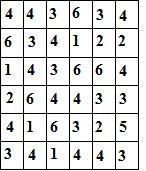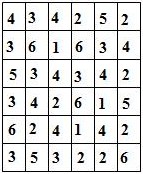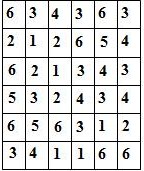Х И Т О Р И  Необходимо вычёркивать повторяющиеся числа, чтобы ни одно из них не встречалось в любой строке или столбце чаще одного раза. Зачеркнутые клетки могут касаться друг друга только углами, но не сторонами. Незачёркнутые клетки должны составлять непрерывное "белое" пространство, то есть ни одна из них не должна быть изолирована от других таких же. ПРИМЕР: ОТВЕТ: 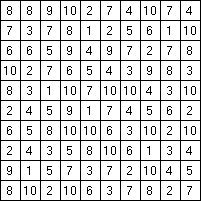ЗАДАНИЕ К У Р О М А СУ ( КУРОДОКУ) Каждая клетка может быть либо белой, либо чёрной. Цель игры определить какие клетки чёрные, соблюдая следующие правила:    • Каждое число на поле показывает, сколько белых клеток видно из этой клетки, включая себя. Клетка видна из другой клетки, если она находится в том же ряду или столбце, и между ними нет чёрных клеток.   • Клетки с числами всегда остаются белыми.   • Чёрные клетки не могут соприкасаться по вертикали или по горизонтали.   • Все белые клетки составляют единое белое поле, то есть соприкасаются по вертикали или по горизонтали. ПРИМЕР: ОТВЕТ: 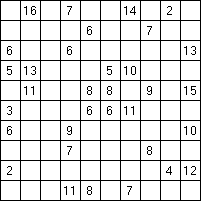ЗАДАНИЕ 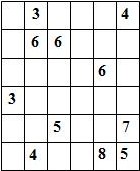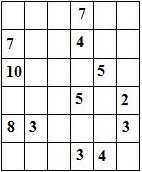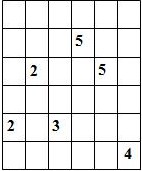ЗАДАНИЕ ЯПОНСКИЕ КРОССВОРДЫ Пользуясь цифрами, расположенными слева и сверху кроссворда, нужно разгадать картинку. Цифры показывают, сколько клеток нужно закрасить. Между закрашенными клетками должна находиться хотя бы одна не закрашенная. ПРИМЕР: 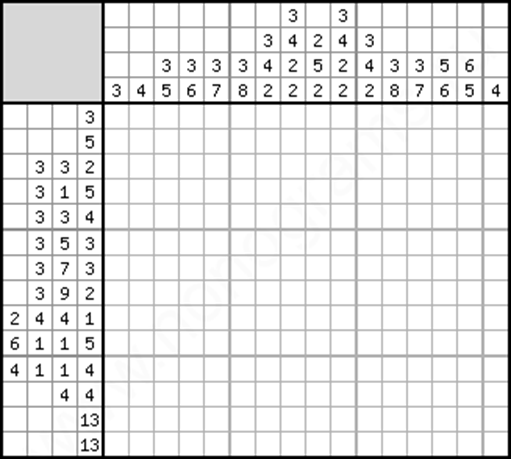ОТВЕТ: К А К У Р О  Необходимо вставить в клетки цифры от 1 до 9, причём некоторые клетки неактивны (такие клетки помечены чёрным цветом или перечеркнуты). В клетках с заданными числовыми значениями правое верхнее значение означает сумму цифр в ряду, а значение снизу слева равно сумме цифр столбца ниже клетки. Например, число 8 можно представить как сумму 1 и 7, 2 и 6, 3 и 5; одинаковые цифры (4 и 4) использовать запрещено. ПРИМЕР: ОТВЕТ: ЗАДАНИЕ 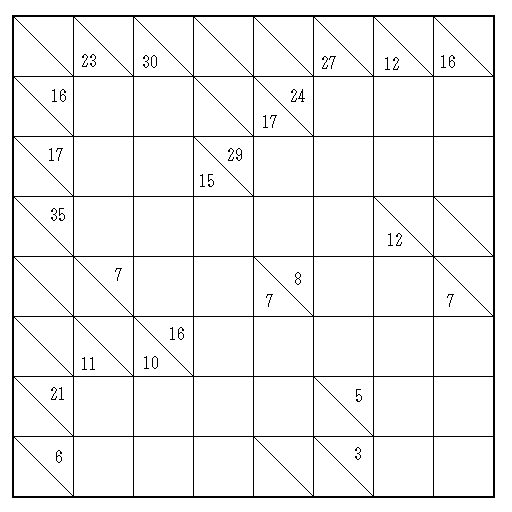Ф И Л Л О М И Н О  Необходимо разбить игровое поле на блоки; блок должен содержать столько клеток, сколько обозначено числом в клетках блока. Блоки, имеющие одинаковый размер, не должны соприкасаться по горизонтали или по вертикали. Клетки, которые изначально не содержали чисел, также могут быть объединены в блоки, необходимые для решения головоломки. ПРИМЕР: ОТВЕТ: 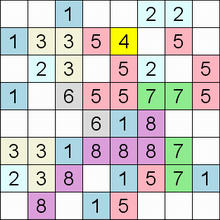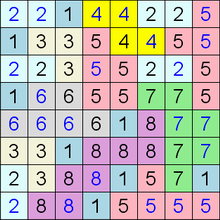ЗАДАНИЕ 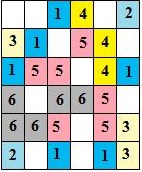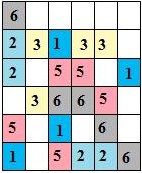СУДОКУ - САМУРАЙ Разновидность головоломки судоку. Игровое поле состоит из пяти квадратов размером 9х9. Цифры от 1 до 9 должны быть расставлены правильно во всех пяти квадратах. ЗАДАНИЕ СУДОКУ Задача - вписать в пустые ячейки цифры от 1 до 9 так, чтобы в каждом горизонтальном ряду, в каждой вертикальной колонке и в каждом блоке, каждая цифра встречалась только один раз. ПРИМЕР: ОТВЕТ: 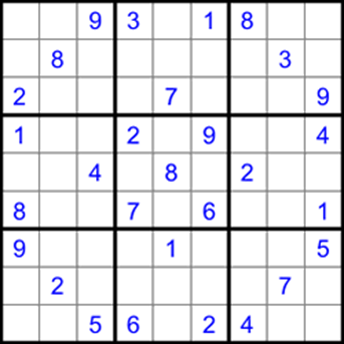ЗАДАНИЕ 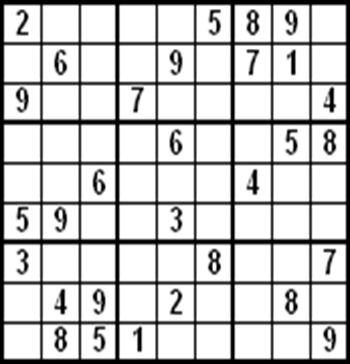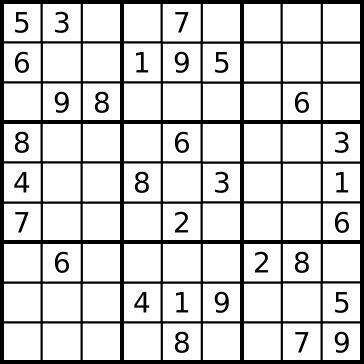КЕН-КЕН  (КЕНДОКИ) Необходимо заполнить сетку цифрами так, чтобы в каждой строке и в каждом столбце они не повторялись. Но возможно повторение чисел в блоке. Число в углу каждого выделенного блока является результатом арифметической операции над цифрами в этом блоке. ПРИМЕР: ОТВЕТ: 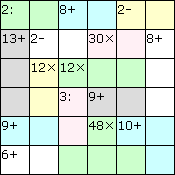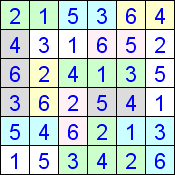ЗАДАНИЕ 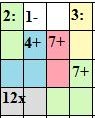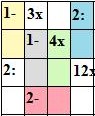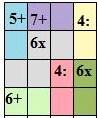ЛАГЕРЬ  Необходимо разместить рядом с деревьями "палатки" (серая клетка), соблюдая следующие правила:  • Число палаток равняется числу деревьев.  • Каждая палатка располагается рядом со "своим" деревом по горизонтали или вертикали, но не по диагонали. Если это условие выполнено, расположение по отношению к "чужим" деревьям значения не имеет.  • Две палатки не могут располагаться в соседних клетках, в том числе и по диагонали.  • Числа сбоку и сверху показывают, сколько палаток находится в этой строке или столбце. ПРИМЕР: ОТВЕТ: 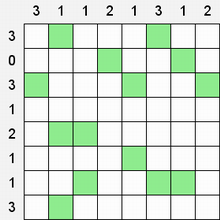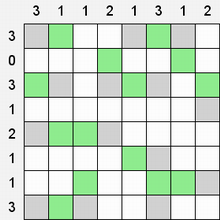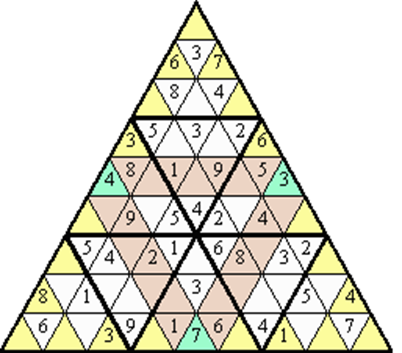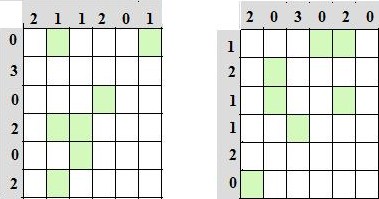ТРИДОКУ Головоломка состоит из девяти больших треугольников; каждый из них содержит девять маленьких треугольников. Цифры от 1 до 9 должны быть расставлены в клетках каждого большого треугольника. Две соприкасающиеся треугольные клетки не должны содержать одинаковых чисел (даже если клетки касаются друг друга лишь одной точкой). ПРИМЕР: ОТВЕТ: ЗАДАНИЕ 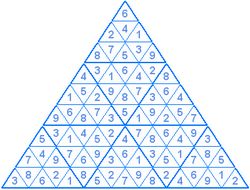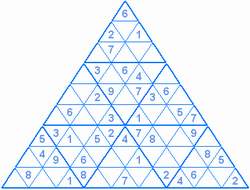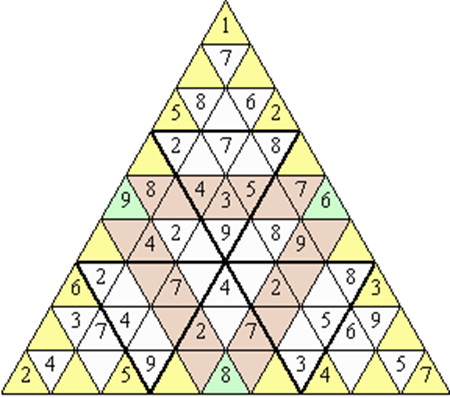ХОШИ Головоломка состоит из шести больших треугольников; цифры от 1 до 9 должны быть расставлены в треугольных клетках каждого большого треугольника. Каждая линия (горизонтальная или наклонная, любой длины, даже прерывистая) содержит неповторяющиеся цифры. ПРИМЕР: ОТВЕТ: 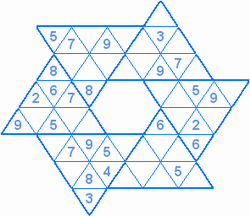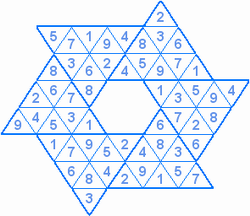ЗАДАНИЕ 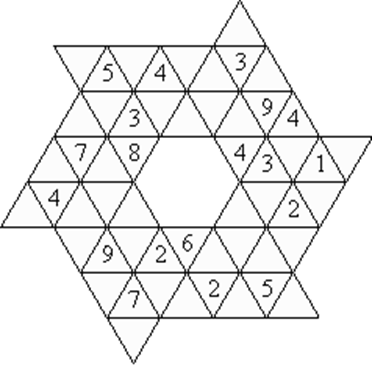 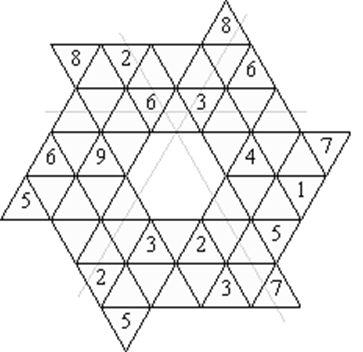 ХИДАТО (ХИДОКУ) Необходимо заполнить все клетки последовательными числами, которые соединены горизонтально, вертикально или по диагонали. В каждой головоломке уже присутствуют наименьшее и наибольшее числа, а также и другие числа, чтобы облегчить процесс разгадывания головоломки. ПРИМЕР: ОТВЕТ: 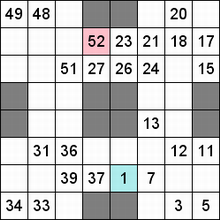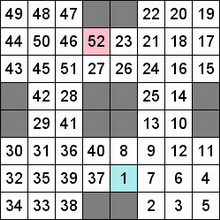ЗАДАНИЕ 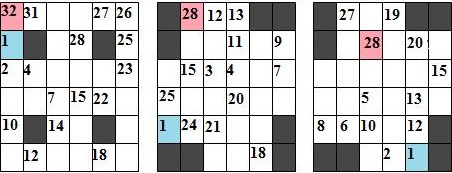Н У Р И К А Б Е  Необходимо восстановить карту, на которой изображено расположение островов, соблюдая следующие правила:   • Информация о каждом острове представлена в виде числа, показывающего количество клеток, которые занимает этот остров.   • Любые два острова могут соприкасаться только углами.   • Все острова содержат в своём описании только одно число.   • Между островами протекает река.   • Все клетки реки должны быть соединены между собой.   • На карте не должно присутствовать ни одного квадрата  размерами 2x2, все клетки которого содержат реку. ПРИМЕР: ОТВЕТ: 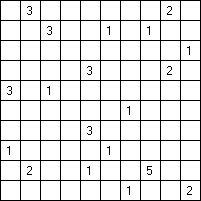ЗАДАНИЕ 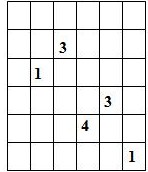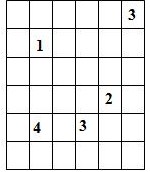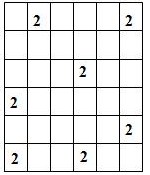ЧИСЛОВОЙ СКАНВОРД Это сканворд, слова в котором состоят из цифр. Определением для такого "слова" служит число - сумма всех цифр, в него входящих. Можно загадать число явно - как в нашем примере, где нужно вписать год события на фотографии. Все цифры в каждом "слове" различны, ни одно из слов не начинается с нуля. ЗАДАНИЕ О Б Л А К А  В сетке произвольной формы необходимо расставить прямоугольники ("облака") так, чтобы они не касались друг друга даже углами. Числа по краям сетки означают количество клеток, занятых облаками. Количество и размер облаков не заданы; известно лишь, что стороны прямоугольников имеют длину не меньше двух. ПРИМЕР: ОТВЕТ: 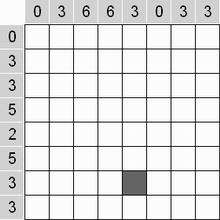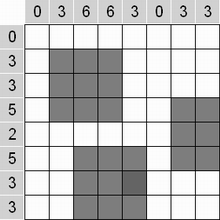ЗАДАНИЕ 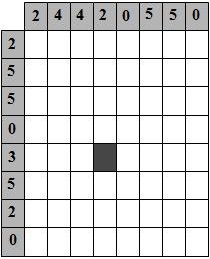Н У М Е Р А Т О Р  Требуется заполнить пустые клетки таким образом, чтобы все числа были соединены последовательно, по горизонтали или вертикали. Перемещение по диагонали не допускается. ПРИМЕР: ОТВЕТ: 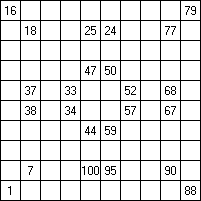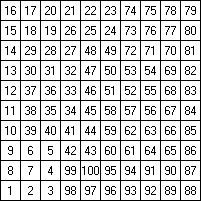ЗАДАНИЕ 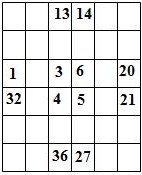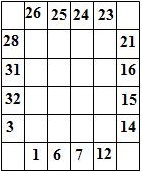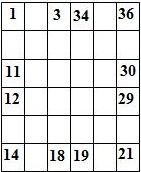Ч И С Л О Б У С  Необходимо заполнить сетку таким образом, чтобы каждый ряд содержал цифры от 0 до 9. В столбцах числа могут повторяться. Число внизу сетки означает сумму всех цифр в столбце. Числа, находящиеся в смежных клетках (даже если клетки соприкасаются лишь по диагонали), должны быть разными. ПРИМЕР: ОТВЕТ: 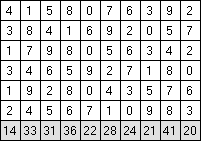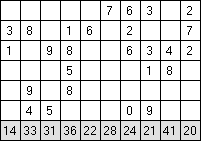ЗАДАНИЕ 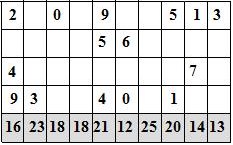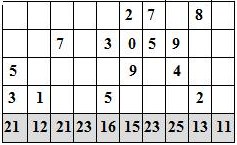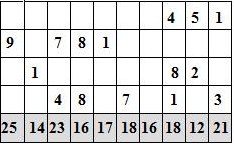КВАДРАТЫ (ШИКАКУ) Необходимо разделить сетку на прямоугольные и квадратные регионы таким образом, чтобы каждый регион содержал только одно число, равное площади этого региона. ПРИМЕР: ОТВЕТ: 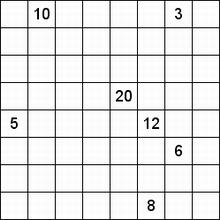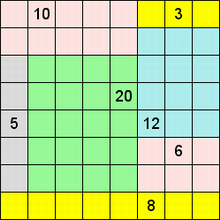ЗАДАНИЕ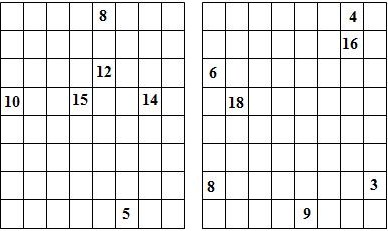