Учебник по математике для 7 класса, рабочие тетради; учебник по алгебре для 7 класса, общественно-гуманитарного направления, А. Н. Шыныбеков, Алматы Атамура, 2007

Название	Учебник по математике для 7 класса, рабочие тетради; учебник по алгебре для 7 класса, общественно-гуманитарного направления, А. Н. Шыныбеков, Алматы Атамура, 2007
Дата	05.04.2016
Размер	233.52 Kb.
Тип	Учебник

Урок алгебры 7 класс

Северо-Казахстанская область

Кызылжарский район

ГУ «Асановская средняя школа»

Учитель Сайдахметова К.Ж

Урок – путешествие «В мир одночленов и многочленов».

Эпиграф урока: « Достижения крупные людям

Никогда не давались легко!»

Цель урока: совершенствовать навыки работы с электронным учебником «Математика 7», обобщение теоретического материала по теме «Одночлен» и «Многочлен» и закрепление на упражнениях.

Задачи:

Образовательная: обеспечить повторение и систематизацию материала темы;
создать условия контроля (самоконтроля) усвоения знаний и умений;

Развивающая: способствовать формированию умений применять приемы сравнения, перенос знаний в измененную ситуацию, развитию мышления, речи,

внимания;

Воспитательная: содействовать воспитанию интереса к математике, активности,

организованности

Тип урока: Урок закрепление

Формы обучения: фронтальная, индивидуальная, работа в группах

Технология: ИКТ

Средства обучения:

компьютер, интерактивная доска, электронный учебник по математике для 7 класса, рабочие тетради;
учебник по алгебре для 7 класса, общественно-гуманитарного направления, А.Н.Шыныбеков, Алматы – Атамура, 2007;

Ход урока

Этапы урока	Деятельность учителя	Деятельность учащихся	Методы и приёмы использования электронного учебника
Организационный	Организация учащихся. Проверка готовности к уроку. Приветствие. Мотивация учащихся на эффективную работу.	Приветствие
Актуализация знаний	1.Сообщение темы урока. Включение электронного учебника. Рефлексия: Выбери из предложенных рисунков тот, который соответствует твоему настроению на начало урока и отметь его. Мне хорошо я готов к путешествию Мне безразлично Я тревожусь, все ли у меня получиться?	Учащиеся выбирают рисунок, соответствующий настроению на начало урока.	Приём акцентирования Модуль 2,3
Актуализация знаний	2. Составление маршрута путешествия А) Верно ли утверждение, определение, свойство? Одночленом называют сумму числовых и буквенных множителе(-) Одночлены, которые отличаются друг от друга только коэффициентами, называются подобными членами. В результате умножения одночлена на одночлен получается одночлен. В результате умножения многочлена на одночлен получается одночлен(-) Алгебраическая сумма нескольких одночленов называется многочленом. В результате умножения многочлена на многочлен получается многочлен. Чтобы разделить многочлен на одночлен, нужно каждый член многочлена умножить на этот одночлен и полученные результаты сложить(-) Чтобы умножить многочлен на многочлен, нужно умножить каждый член одного многочлена на каждый член другого многочлена и полученные произведения сложить. Буквенный множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлен (-) (Графический диктант ^ - да, — нет) Б) Итак, маршрут готов. Отправляемся покорять вершину «Д» - домашняя работа. Соотнесите ответы на экране с номерами заданий. (пауза) Отметьте в маршрутном листе, как справились с д/з. - Ребята, среди перечисленных выражений на экране назовите одночлены. А как называются остальные выражения?	Учащиеся слушают формулировку утверждения, определения, свойства и сравнивают с электронным учебником Учащиеся выполняют работу в тетради и получают Учащиеся проверяют д /з и результат отмечают в маршрутном листе Проверка: учащиеся работают на интерактивной доске На интерактивной доске ряд одночленов и многочленов- учащиеся подчеркивают одночлены, а остальные называют.	Установление соответствия (приём использования шторки) Модуль 2,3 Подмодуль 2 Приём соответствия Приём повторения Приём беседы с учащимися
Применение знаний	3. Вершина «У» - устная работа. 1) Замените букву «М» многочленом так, чтобы полученное равенство было верным: 5а + М = 5а + 3b – 8; b² – bc - М = b² – bc – 7b + 5; М + ( 2a² + 4b – b²) = 3a² + 4ab. 2) В пустое окошко вставьте одночлен так, чтобы полученное равенство было верным: ٠ (a – b) = 4ac – 4bc; 12a³ – 4a²) : =3a – 1; ٠ (2a – b) = 10a² – 5ab.	Учащиеся работают устно: слушают, рассуждают, доказывают Взаимопроверка выполнения задания как «шторка» откроется	Соревнователь ный приём (элемент «шторка»)
Применение знаний	4. Вершина «З» - задание из электронного учебника.	Учащиеся выполняют задания, скопированные на новый лист Самопроверка выполнения задания	Модуль2,3 «Одночлен» «Многочлен» Задание1,2 Использование «Съёмки» и перенос на новый лист задания
Тестирование	5.Вершина «Т» ( Разноуровневая самостоятельная работа, карточка синего цвета, соответствует отметке «3», зеленого цвета – отметке «4», красного цвета – отметке «5»). Контролирует процесс выполнения теста, по окончании осуществляется проверка теста	Учащиеся по группам отвечают на вопросы тестовых заданий Учащиеся выбирают соответствующий цвет карточки и выполняют самостоятельную работу. Цифру, под которой записан правильный ответ надо вычеркнуть в контрольном талоне. Решения записывают в тетрадь. В маршрутном листе отмечают количество правильных ответов.	Самопроверка
	5. Вершина «П» - письмо, а в нем домашнее задание 1. стр. 54–№220(1,2) обязательно 2. № 268(1)* - по желанию.
Анализ урока	Подведение итогов урока. – Ребята! Все вершины пройдены, мы возвращаемся из путешествия. Подведем итог: а) Данное выражение 2х – 3х – 5 одночлен? Обоснуйте. б) А теперь расставьте скобки таким образом, чтобы получился многочлен 1) 2х² – 13х + 15; 2) 5 – х; 3) 15 – х. - Молодцы, ребята, я вижу вы успешно вернулись из путешествия. А с каким настроением вы вернулись? Отметьте свое настроение на рисунках в маршрутном листе. Ребята, кому путешествие понравилось? И я вместе с вами закончила путешествие. И мое настроение Спасибо за урок!	Рассуждение. Рефлексия.	Приём обобщения.

Вариант – 1

(синий цвет)

Упростите выражение 1 – 6:

1. (7х – 4) – (1 – 2х)

6) 9х – 5; 10) 5х – 5; 3) 9х – 3.
2. – 3х³ ٠ ху²

1) – 3х³у²; 17) 3х³у²; 12) – 3х⁴у² .
3. (3х²– 2х + 5) ٠4х³

5) 12х⁶ – 8х⁴ + 20х³; 18) 12х⁵ – 8х⁴ + 20х³; 11) 12х⁵ + 8х⁴ + 20х³.

4. 3а (а + 1) – а²
9) 3а² + 1 – а²; 2) 2а² + 3а; 16) 2а² – 1.

5. (х + 1)(х – 1)
7) х² – 1; 13) х² – 2х – 1; 4) 1 - х².

6. (70 m² – 20mn – 10m) : (10m)

15) 7m – 2n – 1; 8) 70m³ – 2n – m; 14) 7m – 2m – 1.

Вариант – 1

(зеленый цвет)

Упростите выражение 1 – 6:

1. (4ху - 3х²) – ( - ху + 5х²)

3) 5ху – 8х³; 10) 3ху + 2х² ; 6) 5ху – 8х² .
2. – 4а²b ٠(-

ab²)
1) – 2a³b³; 17) 12a²b²; 12) 2a³b³.
3. 12a²(a⁵ – a⁴ – 2a³)
5) 12a¹⁰ – 12a⁸ – 24a⁶; 11) 12a³ – 12a² – 24a; 18) 12a⁷ – 12a⁶ – 24a⁵.
4. (x + 1)(x² + x – 1)

2) x³ + 2x² – 1; 9) x³ + 2x² – 2x – 1; 16) x³ – 2x – 1.
5. (a – 2)(a + 2) – a(a + 1)

4) 4a – 1; 7) – 4 – a; 13) 4 – a.
6. (18a⁴ – 27a³) : (9a²) – (10a³) : (5a)

15) – 3a; 8) a⁴ – 3a; 14) – a² – 3a.
Вариант – 1

(красный цвет)

Упростите выражение 1 – 6:

1. (5,5х³у – 2ху²) – (0,5х³у – 2ху²)
6) 5х³у; 3) 5х³у – 4ху²; 10) 5х³у + 4ху².

2.

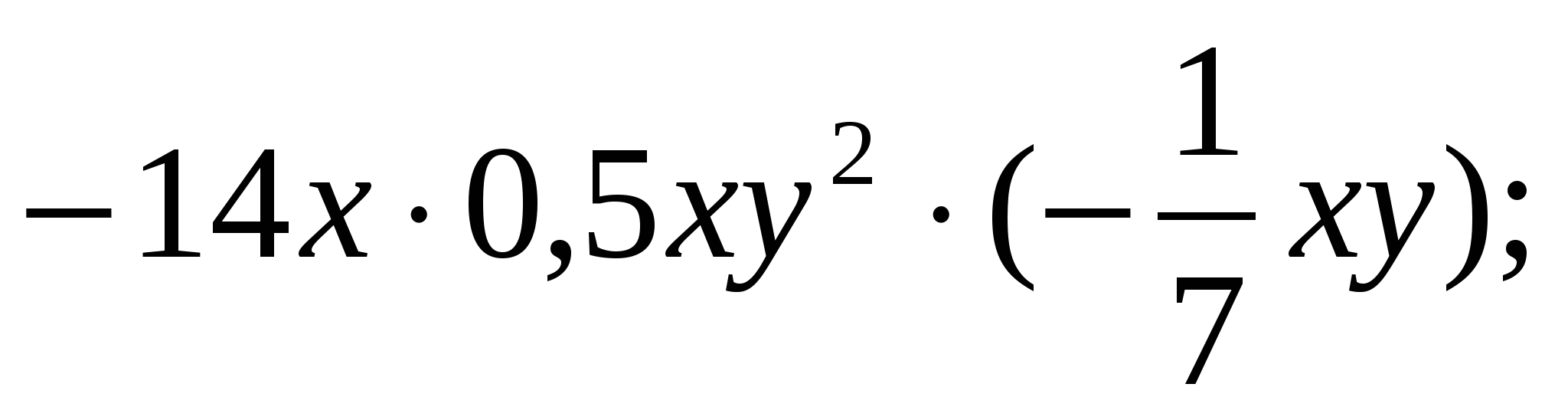
1) 10х³у³; 12) х³у³; 17) – 10х³у².
3. )

5) 6х⁸у – 3х⁴у² + х²у⁶; 18) - 6х⁶у + 3х⁴у³ - х²у⁶; 11) 5х⁶у - 3х⁴у³ + х²у⁶.
4. (х⁴ – х³ – х² – 1)(х + 1)

2) х⁵ - 2х³ – х² – х – 1; 9) х⁵ + 2х³ + х² – х + 1; 16) х⁵ + 2х³ - х² + х + 1.
5. (1 – у)у – (у + 3)(у – 3) - у

7) 9 – 2у²; 4) 9 – у² – у; 13) 2у² + 9.
6. (3х³ + 4х²у) : х² – (10ху + 15у²) : (5у)

8) 5х + у; 14) х + 7у; 15) х + у.

Вариант – 2

(синий цвет)

Упростите выражение 1 – 6:

1. (3х – 2) – (1 – 2х)

10) х – 3; 6) 5х – 3; 3) 5х – 1.
2. – 5х²٠ху²

1) – 5х²у²; 12) – 5х³у²; 20) 5х³у².
3. (5х² – 3х + 7)٠3х²
11) 15х⁴ – 3х² + 21; 5) 15х⁴ – 9х² + 21; 18) 15х⁴ – 9х³ + 21х².
4. 4а(а + 1) – а²

16) 4а² + 1; 9) 3а² – 4а; 2) 3а² + 4а.
5. (5 – х)(5 + х)
4) х² – 25; 7) 25 – х²; 13) х² – 2х – 25.
6. (5m² – 10mn – 5m) : (5m)
8) 25m² – 10n – 1; 14) m – 2n – m; 15) m – 2n – 1.

Вариант – 2

(зеленый цвет)

Упростите выражение 1 – 6:

1. ( - ab + 7a²) – (3ab – 5a²)
3) 2a² – 4ab; 6) 12a² – 4ab; 10) – 2ab + 2a².
2. 6x²b٠(

xb²)
12) – 2x³b³; 1) 2x³b³; 17) – 3x²b².

3. (x⁵ – x⁴– 2x³)(15x²)
5) 15x⁵ – 15x⁴ – 30x³; 11) 15x¹⁰ – 15x⁸ – 2x⁶; 18) 15x⁷ – 15x⁶ – 30x⁵.

4. (a² – a + 1)(a + 1)
2) a³ + 1; 9) a³ – 2a + 1; 16) a³ – 1.

5. x(x + 1) – (x – 3)(x + 3)
4) x – 9; 7) x + 9; 13) 9 – x.

6. (15x⁴ – 25x³):(5x²) – (9х³): (3х)

8) х² – 5х; 14) 5х + х²; 15) – 5х.

Вариант – 2

(красный цвет)

Упростите выражение 1 – 6:
1. (8,5а⁵у² – 3ау³) – (2,5 а⁵у² - 3ау³)
6) 6а⁵у²; 3) 6а⁵у² - 6ау³; 10) 6а⁵у² - 6ау³.

2.

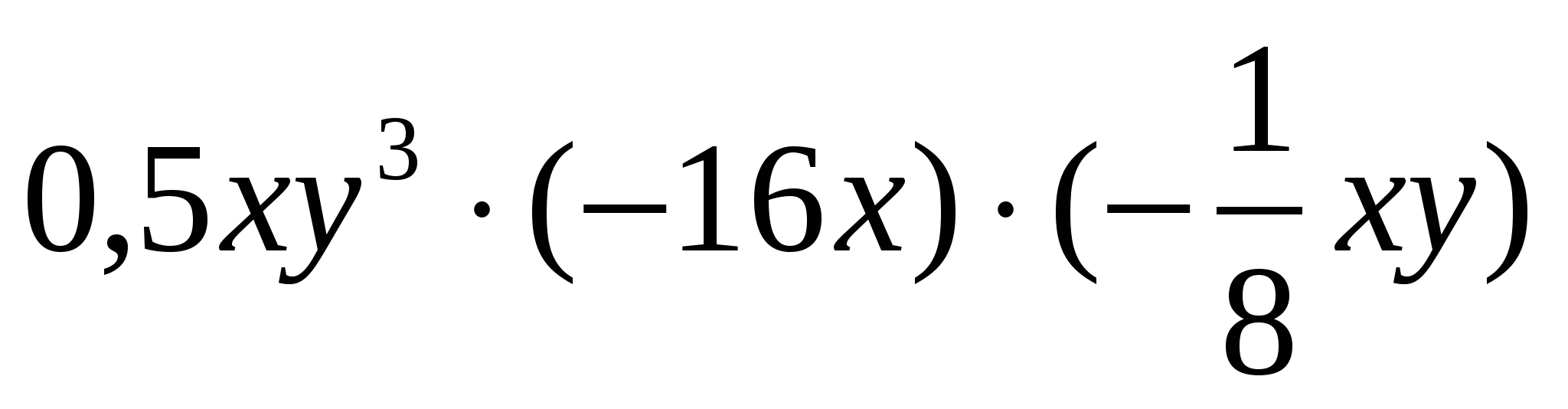
1) – х³у³; 12) х³у⁴; 17) 2х³у⁴.
3. (3х³ – х²у² +

у⁴)٠( - 2х²у)

11) – 6х⁶у + 2х⁴у² – х²у⁵; 5) 6х⁵у + 2х³у³ + х²у⁵; 18) - 6х⁵у + 2х⁴у³ - х²у⁵.
4. (а + 1)٠(а⁵ – а⁴ – а³ – 2)
2) а⁶ – 2а⁴ – а³ – 2а – 2; 9) а⁶ – 2а⁴ + а³ – 2а – 2; 16) а⁶ + 2а⁴ – а³ + 2а – 2.
5. у(3 – у) – 3у – (у + 2)(у – 2)

7) 4 – 2у²; 13) 2у² – 4; 4) 2у² + 4.

6. (3х³ – 2х²у) : х² – (6ху² + 3у³) : (3у²)
8) 3х – 3у; 14) х – у; 15) х – 3у.

(Учащиеся выбирают соответствующий цвет карточки и выполняют самостоятельную работу. Цифру, под которой записан правильный ответ надо вычеркнуть в контрольном талоне. Решение записать в тетрадь.)
Контрольный талон

1	2	3	4	5
6	7	8	9	10
11	12	13	14	15
16	17	18	19	20

Код правильного ответа

№ задания	1	2	3	4	5	6
Ответ	6	12	18	2	7	15

Маршрут путешествия по вершинам знаний

на тему «Мир одночленов и многочленов».
У

чени____ 7 класса ____

^{(фамилия, имя)}
Рефлексия: Выбери из предложенных рисунков тот, который соответствует твоему настроению на начало урока и отметь его.

Мне хорошо я готов к путешествию

Мне безразлично

Я тревожусь, все ли у меня получится?

Задания маршрута:

Построй график движения маршрута (графический диктант).

Да

Нет

Вершина «Д» - домашнее задание __________
(по усмотрению учителя) __________
Вершина «У» - устная работа ___________________

4. Вершина «З» - задание _________________________

Из упр. Подмодулей

1	2	3	4	5
6	7	8	9	10
11	12	13	14	15
16	17	18	19	20

5. Вершина «Т» - тест

1) ________

2) ________

3) ________

4) ________

5) ________

6) ________
6. Самооценка _____________________
7. Общая отметка __________________

8. Рефлексия: Выбери из предложенных рисунков тот, который соответствует твоему настроению после пройденного урока и отметь его.

Мне понравилось, я доволен собой.

Мне всё равно

Мне грустно, я не всё усвоил

Урок математики

Асановская средняя школа,СКО

Класс 7 «б»

Учитель Сайдахметова К.Ж.

Тема: Разложение многочленов на множители

способом группировки

Цели урока:

Образовательная: дальнейшее развитие умений раскладывать многочлены на множители способом группировки;
Развивающая: овладение способом группировки:

а) для контролирования процесса решения задач другими учениками;

б) для обнаружения, исправления ошибок и объяснения своих действий;

Воспитательная: учащиеся должны убедиться, что способ группировки является общим способом для решения большого класса задач.

Оборудование: компьютер, интерактивная доска.

Информационно - образовательная среда: электронный учебник

«Математика-7», модуль «Многочлен»

Ход урока

Этапы урока	Деятельность учителя	Деятельность учащихся	Методы и приёмы
Организационный	Организация учащихся. Проверка готовности к уроку. Приветствие Мотивация учащихся на эффективную работу	Приветствие
Мотивационно - ориентировочный этап	Сообщение темы урока. Включение электронного учебника. Ребята, сегодня на уроке мы рассмотрим способы разложения многочленов на множители - вынесение общего множителя за скобки и способ группировки.	Прослушивание названия темы.	Приём акцентирования
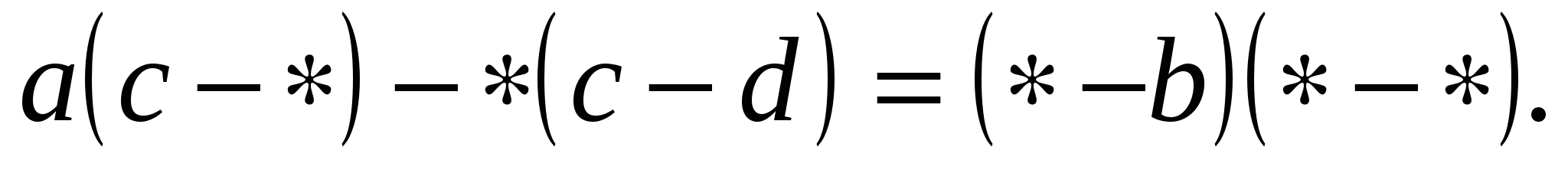
Отработка общего способа	Попробуйте решить ряд заданий. Разложите на множители: а) х² + х; б) а² - 2х + ах - 2а. Вместо звездочек поставьте недостающие одночлены: Проверьте, правильно ли выполнено разложение: 3х + 3ху + ху – у² = (3х - у)(х + у). Найдите ошибку: 3(m - n)² - z(n - m) = (m - n) (3m - 3n - z). Как будем работать: все вместе, в парах или группах?	Ученики выбирают форму работы, 3-5 минут прорешивают задания, затем идет обсуждение решений.	Приём беседы Соревновательный приём
Контроль	Есть ли вопросы? Задание не вызвало у вас затруднений? Тогда предлагаю поработать самостоятельно. 1 вариант. Разложите на множители 1. ab-ac+a. 2. m-n+2p(m-n). 3. x²-xy-5x+5y. 4. a(b-c)+c-b. 5. –b(x-y)-c(y-x). 2 вариант. Разложите на множители 2m²-3mn+m. 3a(b-c)+b-c. 2x²+4xy-ax-2ay. –p-g+a(p+g). x(m-n)+y(n-m). Отложите, пожалуйста, листочки на край парты и положите ручки. Вы проверили свое решение? Выполните, пожалуйста, следующее задание, а затем проверьте свою работу еще раз. Найдите ошибки и приведите верное решение примеров 1-5, в которых выполнено разложение на множители. 1. a) 3a²- 2ab + a = a(3a - 2b); б) 3a² – 2ab +a = a(3a – 2b + 1). 2. a) x – y - 2x(x - y) = (x – y)( – 2x); б) x – y - 2x(x - y) = (x – y)(1 – 2x). 3. а) 3a² – 6ab – ac + 2bc = 3a (a-2b) – c(a-2b)=(a-2b)(-a+2b) б) 3a² – 6ab – ac + 2bc = 3(a²– 2ab) +c(-a+2b) в) 3a² – 6ab – ac + 2bc = 3a (a-2b) + (-a+2b)=(a-2b)(3a+1). 4. а) – x – y – a(x+y) = - (x+y) – a(x+y) = (x+y)(-1-a). б) – x – y – a(x+y) = - (x+y) – a(x+y) = (x+y)(-1-a)= - (x+y)(a+1). 5. a) p(a-b) – m(b-a) = p(a-b) + m(a-b) = (a-b)(p+m). б) p(a-b) – m(b-a) = (a-b)(p+m). в) p(a-b) – m(b-a) = (a-b)(p-m).	Учащиеся выполняют задания самостоятельно Да Класс обсуждает решение каждого примера. Учащиеся находят ошибки и говорят, как их необходимо исправить. Эти решения убрали и открыли задание самостоятельной работы.	Задания на интерактивной доске (можно выбрать из заданий или из теста) Модуль «Многочлен» Подмодуль «Разложение на множители» Приём повторяющихся условий
Самооценка	Довольны ли вы результатами? Кто нашел ошибки в своих решениях? Можно ли идти дальше?	После обсуждения ученики возвращаются к своим листочкам, проверяют решение, исправляют ошибки зеленой пастой и сдают учителю. Мы считаем, что можно перейти к изучению нового материала и параллельно продолжить отработку открытых способов.
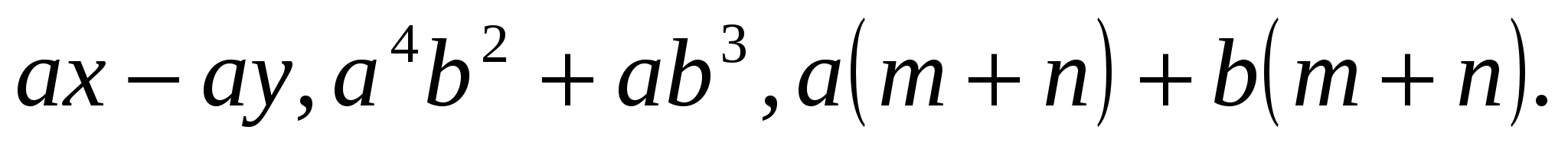
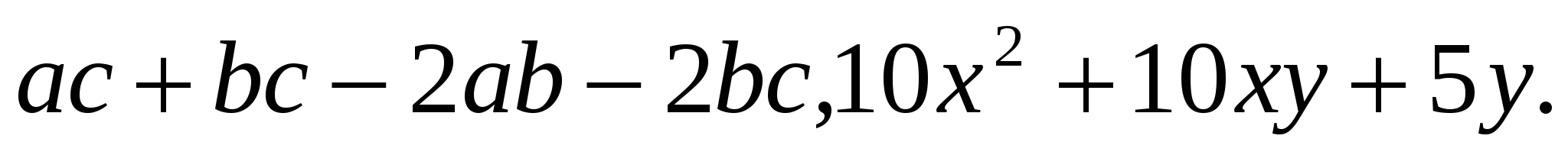
Актуализация знаний	Я выписала различные алгебраические выражения. Проклассифицируйте их, пожалуйста, по способам разложения. ax-ay; a² +2ab+b² ac+bc-2ab-2bc 10x² +10xy+5x+5y а² -2ab+b² a² - 16 a² – b² a⁴ b² + ab³ x² +4x+4 c² +2c+1 p² - 4pg+4g² a(m+n)+b(m+n) x² - 6x + 9. Учитель. Какую форму работы выберем? По какому принципу будем объединяться в группы? Учитель подводит итоги работы. Для групп: Показываются решения.	Групповую. Учащиеся садятся группами, распределяют обязанности и приступают к работе. Каждое выражение записано на отдельной карточке и ученики просто раскладывают их по группам. Каждая группа распознаёт способы разложения и рассказывает о результатах классификации. Учащиеся говорят, что для остальных групп способы необходимо найти Учащиеся разбирают, записывают решения	Модуль «Многочлен»
Операционально-исполнительный	Предлагаю начать с разложения на множители многочлена а²-2ab+b². Если группа будет испытывать затруднения, вы можете воспользоваться подсказками из модуля – электронный учебник. В дальнейшем эти универсальные способы мы будем применять на решениях упражнений из учебного пособия Даётся домашнее задание	Учащиеся слушают, рассуждают и применяют при разборе упражнений из учебника	Приём создания проблемной ситуации Образцы решения Модуль «Многочлен» «Образцы решения задач» Приём демонстрации Выделение главного
Анализ урока	Подведение итогов урока: Чему вы научились? Над чем ещё предстоит поработать? Выставление оценок	Рассуждение Рефлексия	Приём обобщения

Урок математики

Асановская средняя школа,СКО

Класс 7 «б»

Учитель Сайдахметова К.Ж.

Тема: Возведение в квадрат суммы и разности двух выражений

Цели урока:

Образовательная: обеспечить усвоение материала всеми учащимися; учить и научить каждого ученика самостоятельно добывать знания;
формировать навыки, умения, которые обеспечивают успешное выполнение деятельности учить и научить каждого ученика самостоятельно добывать знания;
формировать навыки, умения, которые обеспечивают успешное выполнение деятельности.
Развивающая: способствовать развитию математического кругозора, мышления: умения анализировать, выделять главное, сравнивать, обобщать и систематизировать, развивать устную и письменную речи, внимание и память; продолжить работу по развитию умения самостоятельно приобретать новые знания; использование для достижения поставленной задачи уже полученных знаний.

Воспитательная: содействовать воспитанию интереса к математике, активности, дисциплинированности, честности, ответственности за свой труд и труд одноклассника, воспитание навыков самоконтроля и взаимоконтроля.
Оборудование: компьютер, интерактивная доска.

Информационно - образовательная среда: электронный учебник

«Математика-7», модуль «Многочлен»

Ход урока

Этапы урока

Деятельность учителя

Деятельность учащихся

Методы и приёмы

Организационный

Организация учащихся.

Проверка готовности к уроку (рабочее место, внешний вид);

Организация на внимание.

Взаимное приветствие

Мотивация учащихся на эффективную работу

Приветствие

Этап подготовки к активному материалу

Сообщение темы урока.

Включение электронного учебника.

Ребята, проверим знания о возведении выражений в квадрат, приведении подобных.

Верны ли утверждения?
1) (-7)² = -7² (да)
2) (2а)² =- 2а²

(нет)
3) (8)² = 64 (да)
4) (-3х)² =- 9х² (нет)
5) ав + ва = 2ав (да)
6) (а + в)² =) (а + в) (а + в) (да)
7) -6а + 10а = 16а (нет)
8) 8mn - 10 mn = -2mn (да)
9) -7ху - 3ух = -10ху (да)

«Устные упражнения».
Устно выполняют упражнения.
1) 5 = 5 . 5 = 25
а² = а.а
(5а)² = 5а 5а = 25а²
(2 + 3)² = (2 + 3)(2 + 3) = 25
2) (а + в)² = (а + в)(а + в) = аа + ав + ва + вв = а²+ 2ав+в²
3) (х + у)² = (х + у)(х + у) = хх + ху + ух + уу = х²+2ху+у²
Какие закономерности видны в примерах 2 и 3?

Проверитьподготовку учащихся к активному материалу.

Отвечают на вопросы.
Учащиеся поднимают руки и дают ответы

Приём акцентирования

Этап усвоения нового материала

С помощью создания проблемной ситуации подвести учащихся к квадрату суммы и разности двух выражений.
Учитель обращает внимание учащихся на доску, где записаны примеры в 3 столбца, 2 и 3 столбцы закрыты. Ребята объединяются в 3 группы и получают задание: найти произведение данных многочленов (затем через некоторое время открыть 2 столбец).

I	II	III
1)(m + n)(m +n) = 2)(c + d)(c + d)= 3) (p + g)(p + g) = I (8 + m)(8 + m) = II (n + 5)(n + 5) = III (a + 3)(a + 3) =	=m² + 2mn +n² = c² + 2cd + d² = p² + 2pg + g² =64 + 16m+ m² =n² + 10n + 25 = a² + 6a + 9	=(m - n)² =(c + d)² =(p + g)² =(8+m)² =(n + 5)² =(a + 3)²

Вопросы:
1) Есть ли общее в условиях и ответах?
Можно ли выражения в 1 столбце записать короче? (Открыть 3 столбец). Анализируем 2 столбец.
1) Что явилось результатом умножения? (Трёхчлен)
2) 1-й член - квадрат первого выражения
2-й член - удвоенное произведение 1 и 2 выражений
3-й член - квадрат второго выражения
Задание: Записать общую формулу
(а+в)² = а² +2ав + в²
3) А если возвести в квадрат (а - в)²,(в - а)²
4) Что мы получим, если мы заменим в 1 и 3 столбцах знаки «+» на «-»?
5) В каком месте стоит знак «-»?
6) Изменится ли результат, если возвести в квадрат (-а-в)? Мы знаем, что (-а)² =а², тогда (-а - в)² = а² + 2ав + в²
Подведём итоги. Как читается формула квадрата суммы и разности двух выражений?

Учащиеся внимательно смотрят на доску и находят произведение данных многочленов. Работают по группам.

Слушают формулировку и запись правил в электронном учебнике

Приём создания проблемной ситуации

Приём выделения главного

Приём обобщения

Приём демонстрации

Открываем электронный учебник

Прослушиваем правила

Модуль «Многочлен»

Подмодуль

«Формулы сокращённого умножения»

Этап первичного закрепления новых знаний

Отработать навыки применения возведения в квадрат суммы и разности двух выражений, и закрепить их при помощи простейших примеров.
Игра «Открой окно» №340
⁮+2ас+с²m²-⁮+n² а²+2са+⁮

х²-4ху+⁮ ⁮+14c+49 k²-⁮+9

Учащиеся заполняют пустые клетки, записывают примеры в тетрадях, предварительно проговорив

Задания на интерактивной доске

(можно выбрать из заданий или из теста)

Модуль «Многочлен»

Подмодуль «Формулы сокращённого умножения»

Приём частичного варьирования

Этап закрепления новых знаний

Установить, усвоили ли учащиеся возведение в квадрат суммы и разности двух выражений.
1) Дидактическая игра в парах.
«Расшифровка»

Каждая пара учеников должна решить свой пример. Найти в схеме букву, соответствующую ответу и нужно поставить её под номером своей карточки. Полученное имя принадлежит известному математику.
Карточки
Е 1) (в² + 2а²)²
К 3) (а² - 3в)²
И 5) (а - 3в)²
В 2) (2в² + 3а)²
Л 4) (2а - 3в)²
Д 6) (2в - 3а)²
Е в⁴ - 4а² в² - 4а²
Д 4в² - 12ав + 9а²
Л 4а² - 12ав + 9в²
К а⁴ - 6а² в + 9в⁴
И а² - 6aв + 9в²
В 4в² - 12в² а + 9а²
1 2 3 4 5 6
Е В К Л И Д

Примеры решают на местах в парах, помогая друг другу.

Можно запись приготовить на чистом флипчарте

Соревновательный приём

Тестирование

Выберитe себе вариант, внимательно прочитайте задание. К каждому заданию даны три ответа, из которых один верный. Решите задание, сравните полученный ответ с предложенным.
I вариант

	Задания	Ответ
А	Б	В
1) 2) 3)	(2а +в)² (х - 1)² (2m+3)²	2а² +2ав+в² х² + 2х +1 4m²+12m+9	4а²+ 2ав +в² х²-2х+ 1 2m²+12m+9	4а²+4ав +в² х²-х + 1 4m²+6m +9

II вариант

	Задания	Ответ
А	Б	В
1) 2) 3) 4)	(с + 8)² (12 - р)² (10z+3t)² (-а+5х)²	с²+8с+16 24-24р +р² 100z²+60zt+9t² -а²+30ах+25х²	с²-6с+64 144-24р + р² 100t²-0zt+9t² 9а²-30ах+25х²	с²+16с+64 144-2р+р² 20z²+60zt+9t² 9а²-5ах+25х²

III вариант

	Задания	Ответ
А	Б	В
1) 2) 3) 4) 5)	(7у+6)² (- 3m+4n)² (6а- 1/6)² (m²-6n)² (-0,2х-а)²	49у²-84у+36 9m²+24mn+16n² 36а² - 2а + 1/36 m² - 12mn+ 36n² -0,04х²-2ах-0,25а²	49у² + 42у+ 36 9m²-4mn+16n² m⁴-12mn+36n² 0,4х²+2ах+25а²	49y + 84y + 36 9m² -12mn -6n² 36a² + 2a +1/36 m² - 12mn +6n² 0,04²+2ах+0,25а²

Бланк ответов
Фамилия, имя:
Вариант:

задания	1	2	3	4
ответа 1 в.
ответа 2 в.
ответа 3 в.

В бланке ответов под номером задания поставьте букву в клеточке, которая cooтветствует выбранному ответу

Учащиеся отвечают на вопросы тестовых заданий

Приём дифференцирования

Анализ урока

Сообщение учашимся домашнего задания

Подведение итогов урока:

Что нового мы узнали?

Чему вы научились?

Над чем ещё предстоит поработать?

Выставление оценок

Урок окончен.

Рассуждение

Рефлексия

Приём обобщения