Геометрия и оригами
 Скачать 151.8 Kb. Скачать 151.8 Kb.
|
 Муниципальное казённое учреждение управления образования Джидинского района Муниципальное казённое учреждение управления образования Джидинского районаМуниципальное бюджетное образовательное учреждение «Боцинская средняя общеобразовательная школа» Тема: «Геометрия и оригами». Секция: Геометрия Автор: Доржиева Софья, ученица 11 класса Руководитель: Зиннатова Надежда Рафиковна, учитель математики. 2014 г. С О Д Е РЖ А Н И Е Введение …………………………………………………………….……..…..…1-2 1. История возникновения оригами ………………………………….………..……3 2. Оригами – это математика? …………………………………………..…………4-5 3. Модульное оригами …………………………………..…………………………. 6 4. Решение задач с помощью оригами…………………………………………….7-8 Заключение ………………………………………………….…………….…..…… 9 Приложение. Список используемой литературы. Японская мудрость издревле гласит: "Великий квадрат не имеет пределов". Попробуй простую фигурку сложить, И вмиг увлечёт интересное дело. Введение. Оригами – это японское искусство создания моделей различных предметов, животных, птиц, цветов путем сгибания листа бумаги. Единственный рабочий материал - это бумага, единственный инструмент - руки. Уникальное занятие складывать своими руками красивые игрушки и геометрические фигуры. При изготовлении фигурок оригами развиваются воображение, мелкая моторика рук, пространственное мышление, воспитывается вкус, аккуратность, трудолюбие, что и делает изучение использования оригами актуальным для исследования. Приобретенные во время складывания навыки можно использовать на уроках по математике и конструированию. Занявшись этим искусством, я увидела, как сильно оригами связана с геометрией. С оригами можно знакомиться и повторять основные геометрические фигуры: треугольник, прямоугольник, квадрат, ромб, четырехугольник. Понятия: сторона, угол, вершина угла, диагональ, центр фигуры их свойства. В настоящее время можно сказать, что математическое образование является основным для людей многих профессий, поэтому большое внимание уделяется изучения основ арифметики, геометрии и алгебры. Особую актуальность приобретает проблема обучения элементам геометрии и повышение уровня математических знаний в целом. В геометрическом материале много общего с художественным восприятием мира, поскольку большое место в геометрии принадлежит образному мышлению. Искусство оригами как нельзя лучше подходит для решения данных задач. Еще в XIX веке немецкий педагог Ф.Фребель основал интегрированный курс обучения математике при помощи оригами, на основе которого можно улучшить и упрочить геометрические знания и умения. Актуальность исследования заключается в том, что позволяет расширить наши знания о оригами и геометрии, умение с помощью обычного листа решать геометрические задачи. Цель исследования – освоить технику оригами и использовать в жизни. Задачи: - изучить историю оригами; - ознакомиться с техникой оригами; - научиться создавать изделия оригами; - выявить связь оригами и геометрии; - найти способы применения оригами в повседневной жизни. -выяснить насколько ученикам нравятся занятия оригами, сделать выводы. Объектом исследования является искусство оригами. Предметом исследования является использование оригами в повседневной жизни. Гипотеза: Занятие оригами развивает творчество, интеллект, учит труду. Практическая значимость. Искусство оригами помогает создавать разные изделия и применять эти знания в учебе. Методы исследования:
Методы и приёмы:
Официальной датой “появления” бумаги в Китае считается 105 г. до н.э. А в 610 году японцы уже производят собственную бумагу, которая по качеству превосходит китайскую. Первая крупная бумажная фабрика в Токио возникла в 1870году. В древности, в Китае бумагу использовали в религиозных обрядах. Не случайно первые оригами появляются в храмах. Один из ритуалов с их использованием состоял в изготовлении коробочек санбо, которые наполняли кусочками рыбы и овощей, для жертвоприношения богам. Это искусство в Японии стало традицией, которая передавалась из поколения в поколение, в основном по женской линии. Первым японским изданием по оригами считается книга “Сенбадзуру ориката” (1797г., “как сложить тысячу журавлей”). Автором считается настоятель храма Рокан. Во второй половине XIX века оригами вышло за границы Японии. В России так получилось, что большинство взрослых оригамистов - педагоги, а юные складыватели - их ученики. Оригами распространяется среди преподавателей и рассматривается как прием обучения и развития учащихся. Самые крупные центры оригами в России находятся в Москве и Санкт-Петербурге. Геометрия в первоначальном своем значении понималась как наука о фигурах, о взаимном расположении и размерах их частей, а также о преобразованиях фигур. История геометрии теряется в глубокой древности, но колыбелью ее, несомненно, является Восток. Геометрические сведения и факты в основном сводились к правилам о вычислении площадей и объемов, и надо полагать, что эти правила носили больше эмпирический, чем логический характер. В VII в. до н. э. геометрические сведения были, по мнению греческих историков, перенесены из Египта и Вавилонии в Грецию. Греческие философы стали знакомиться с египетской и вавилонской мудростью. С этого времени начинается период развития геометрии – период систематического изложения геометрии как науки, где все предложения доказывались. Само название "оригами" происходит от двух японских слов "ори" и "ками" и в буквальном переводе означает "сложенная бумага". И это не случайно, так как сгибание является простейшей операцией с листком бумаги, которая не требует от человека никаких навыков, кроме воображения и, как не странно, эта простейшая операция порождает своеобразную геометрию, не менее богатую, чем геометрия циркуля и линейки. Сначала кажется, что возможности перегибания включают в себя всю геометрию одной линейки, однако это ошибка. В некоторых случаях складки таят в себе также возможности циркуля, хотя и не позволяют проводить непосредственно дуги окружности. И чем дальше погружаешься в эту необычную геометрию, тем все больше приходишь в восхищение от разнообразия забавных и серьезных задач, которые удается решить. С помощью оригами есть возможность показать, что математика не сухая наука, а красота и гармония.
В наше время в Японии, США и других развитых странах обучение геометрии при помощи оригами практикуется во многих школах. Если в прошлом математика применялась в довольно ограниченном числе областей жизни человека, будучи, следовательно, необходимой сравнительно небольшому числу специалистов, то в современную эпоху математика проникла во все те области, в которых практикуется рациональное мышление, и этот процесс, находящийся в постоянном развитии, требует соответствующей математической подготовки. Простые базовые формы
Видя эти формы понимаешь, что на занятиях по математике при помощи оригами можно повторить следующие понятия: – горизонтальные, вертикальные, наклонные линии; – сложи квадрат разными способами, покажи смежные стороны, диагональ; – квадраты; – все виды треугольников. На первом этапе в ходе изучения геометрии с использованием оригами знакомимся с основными геометрическими фигурами (треугольник, прямоугольник, квадрат, ромб, четырехугольник), понятиями (сторона угол, вершина угла, диагональ, центр фигуры), их свойствами и учимся основам техники оригами. На втором этапе развиваем систему знаний, умений и навыков, приобретенных на начальной стадии обучения. Работе по схемам, процессу складывания плоскостных фигур. Эта деятельность направлена на развитие восприятия, которое связано с различными операциями мышления. На этой ступени важно уделить внимание ознакомлению с орнаментами, которые очень красивы по своей форме. Складывая их в различных комбинациях, можно получить многогранники. При этом развивается пространственное воображение, что способствует успешному усвоению стереометрии в старших классах. Важность этой ступени состоит в том, что здесь особое место занимает метод решения задач на построение без помощи циркуля и линейки. Особая ценность этого метода в том, что он позволяет построить правильные многоугольники, построение которых с помощью циркуля и линейки затруднительно, а в некоторых случаях невозможно. Таким образом, навыки, накопленные во время обучения на первом и втором этапах, позволят нам успешно обучаться на третьем этапе. На третьей этапе изучения геометрии с использованием оригами ведется целенаправленная работа по формированию содержательного логико-математического мышления. Большое значение для развития воображения играет изготовление геометрических фигур, в которых прослеживается определенная закономерность расположения модулей, наглядное восприятие которых помогает понять эту особенность и справиться с геометрическими задачами. Сюда входят построения правильных, полуправильных и неправильных многогранников, их сечения, нахождение площадей боковых поверхностей и объемов геометрических тел.
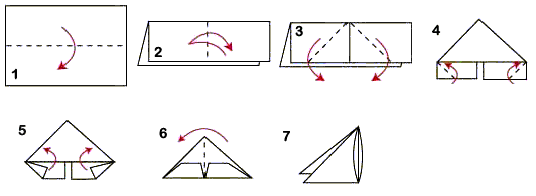
Модульное оригами — техника складывания оригами, которая, в отличие от классического оригами, использует в процессе складывания несколько листов бумаги. Каждый отдельный листок складывается в модуль по правилам классического оригами, а затем модули соединяются путем вкладывания их друг в друга, появляющаяся при этом сила упругости не даёт конструкции распасться. Снятие ограничения на количество листов позволяет с большей лёгкостью создавать крупные модели со сложной структурой. Модульное оригами вошло в моду в последние 20 лет. Оригами является поистине универсальным конструктором, поскольку из всего одной детали (листа или квадрата бумаги) можно сделать что угодно. Отдельная бумажная деталь называется в этом случае модулем (от латинского слова modulus – такт, ритм, мера, модуль). Модули могут быть одинаковыми и составлять вместе орнамент, звезду, правильный многогранник. Разные модули обычно используются для составления сложных конструкций. В этом случае говорят о гетеромодульном оригами. Сегодня существует множество игрушек-трансформеров и мозаичных картинок, все творчество работы с которыми заключается в механическом соединении готовых элементов. Такие игры собираются, раз и навсегда, а сам ребенок не участвует в их разработке и изготовлении. Игра, которую ребенок сделает сам, окажет, несомненно, большее воспитательное и эстетическое воздействие, чем любая купленная в магазине. Модульное оригами это вид объемного оригами. Готовятся одинаковые модули, которые затем вкладываются один в один. Клей не используется.Схема: | |||||||||||||||||||||||
| | Линия сгиба "долиной", "на себя" |  |
| | Стрелка сгиба "долиной", "на себя" | |
| | Совместить отмеченные точки |  |
| | Согнуть и разогнуть |  |
Оригамское решение
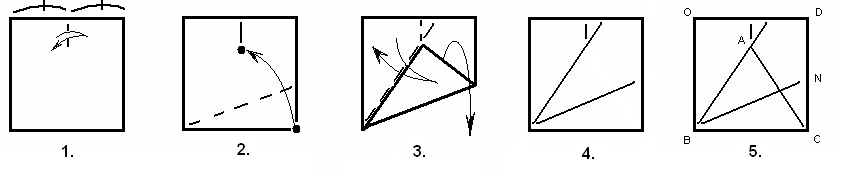
Наметьте сгиб, делящий верхнюю сторону квадрата пополам.
Совместите вершину правого нижнего угла квадрата с некоторой точкой намеченной линии сгиба.
Перегните левую верхнюю часть фигурки и вернитесь в исходное положение квадрата.
Проверьте результат. Вершина левого нижнего угла квадрата линиями сгиба разделена на три равных угла.
Математическое обоснование
Используя чертеж рис. 5, можно записать: ВАС – равносторонний, значит АВС=600.
ОВА=900-600=300, ABN=300, ОВА= ABN= NBC=300.
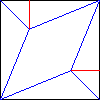
Итак, данным методом мы разделили угол квадрата на три равные части. Продолжением данной задачи является задача построения равностороннего треугольника в квадрате.
Деление листа бумаги на 5 частей.
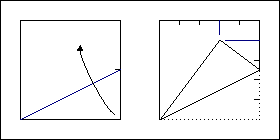
Деление стороны квадрата на четыре равные части. Для этого достаточно их поделить пополам, а затем, каждую из половинок снова пополам. Именно так происходит, когда мы складываем базовую форму дверь.
Как легко догадаться, деление квадрата на пять частей с помощью складывания представляет собой гораздо более сложную задачу. Ее решение изображено на рисунке. Попробуйте сами доказать, что таким образом мы действительно разделим квадрат именно на пять частей.
Заключение.
Работая над данной темой я выделила наиболее существенные моменты. Оригами как основа различных направлений искусства является наиболее логичной и гармоничной формой изучения геометрии. Логика здесь выступает как средство подтверждения наглядности и практической значимости. Выполняя геометрические фигуры в технике оригами, знакомятся с новыми геометрическими понятиями, основными определениями и наглядно изучают закономерности поведения двухмерной плоскости в трехмерном пространстве. Правильно гласит великая китайская мудрость: я слышу и забываю, я вижу и запоминаю, я делаю и понимаю. В голове удерживаются только те знания, которые применяются на практике.
Для изготовления изделий из бумаги могут применяться разные техники – такое занятие не надоест и не покажется скучным.
Собственноручное изготовление бумажных изделий – отличный способ самовыражения, доступный всем. Такое хобби хорошо развивает художественный вкус, фантазию и воображение, мелкую моторику рук, усидчивость и аккуратность.
Темп современной жизни очень велик: одни дела в течение дня стремительно сменяются другими. И в повседневной суете очень важно находить время для любимых занятий. Изготовление изделий из бумаги – это творчество, возможность выразить себя в великолепных работах, обрести душевную гармонию
Моя работа актуальна, предрасполагает воспитанию позитивных качеств личности, а также способствует общению людей, объединенных решением поставленных задач.
Список используемой литературы.
1. О. В. Весновская Оригами: орнаменты, кусудамы, многогранники. -Чеб.: изд. «Руссика», 2003г., 52с.
2. В. А. Гусев Методика обучения геометрии. - М.: изд. «Академия», 2004г, 376с.
3. //Нужна ли школе 21-го века Геометрия? (И. Ф. Шарыгин) Математическое
просвещение. №3, вып. 8.-М.: МННМО, 2004 -264с., С37-52.
4. В. В. Нуркова и Н. Б. Березанская Психология. -М.: изд. «Юрайт», 2004г., 498с.
5. С. Н. Белим Задачи по геометрии, решаемые методами оригами. – М.: изд. «Аким», 1998г., 66с.
6. Колягин Ю.М., Тарасова О.В. Наглядная геометрия и ее роль, и место, история возникновения. - Журнал «Начальная школа» №4, 2000г.
7. Глейзер Г.Д. Каким быть школьному курсу геометрии / Г.Д. Глейзер // Математика в школе. – 1991. - №1. - С. 68 – 71
8. Бескин Н.М. Методика геометрии с приложением главы «Методика преподавания наглядной геометрии А.М. Астряба» / Н.М. Бескин. – М.: Учпедгиз, 1947. - 274с.
9. https://trozo.ru/archives/34530#more-34530
ПРИЛОЖЕНИЕ.
Анкетирование.
1. Ты знаешь, что такое оригами?
____________________________________________________________________
2. Ты пробовал заниматься оригами?
____________________________________________________________________
3. Ты знаешь, что такое модульное оригами?
____________________________________________________________________
4. Ты знал, что можно с помощью оригами решить геометрические задачи?
____________________________________________________________________
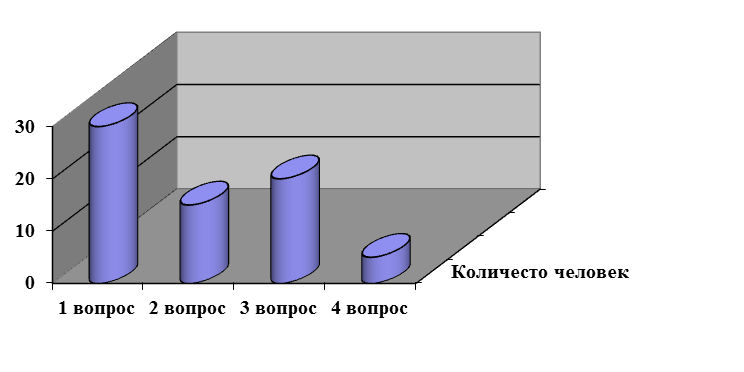
Результаты анкетирования.
Я провела анкетирование среди учащихся 5-11 классов МБОУ»Боцинская СОШ». По результатам анкетирования можно сказать следующее: у всех учащихся есть представление, что такое оригами, но не все знают, что такое модульное оригами. Многие пробовали заниматься оригами, но не у всех получалось. 25 учащихся не знали, что с помощью оригами можно решить геометрические задачи. Мой проект всем понравился, всех он заинтересовал. Теперь нам задачки по геометрии по силам!