|
Согласовано утверждаю
Муниципальное автономное общеобразовательное учреждение
Средняя общеобразовательная школа № 147 г. Челябинска
СОГЛАСОВАНО УТВЕРЖДАЮ
Заместитель директора по УВР Директор МАОУ № 147
__________/С.Г. Мазепова ___________/Е.А.Рожков
«___»___________2012 г. «___»__________2012 г.
Рабочая программа индивидуально-групповых занятий по алгебре и началам математического анализа для 10а,б классов на 2012-2013 учебный год
Универсальный модуль. Социально-правовой модуль.
Составитель рабочей программы: учитель математики высшей категории Казак Вадим Михайлович
Рассмотрена на заседании МО учителей естественно-математических дисциплин
Протокол № ___ от «___»______________2012г.
Руководитель МО: _____________/ Т.Н. Токарева
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа индивидуально-групповых занятий по алгебре и началам математического анализа в 10 а и 10 б классах составлена на основе следующих нормативно-правовых и инструктивно-методических документов:
Приказ МО РФ №1089 от 05.03.2004 г. «Об утверждении Федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования».
Федеральный компонент государственного стандарта среднего (полного) общего образования по математике. Сборник нормативных документов. Математика. /Сост. Э.Д. Днепров, А.Г. Аркадьев.- М.: Дрофа, 2007.
Примерные программы среднего (полного) общего образования по математике. Сборник нормативных документов. Математика. /Сост. Э.Д. Днепров, А.Г. Аркадьев.- М.: Дрофа, 2007.
Приказ МО и Н РФ №2885 от 27.12.2011 г. «Об утверждении федеральных перечней учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию, на 2012/2013 учебный год».
Письмо МО и Н Челябинской области от 31.07.2009 № 103/3404 «О разработке рабочих программ курсов, предметов, дисциплин (модулей) общеобразовательных учреждений Челябинской области».
Приложение к письму МО и Н Челябинской области от 18.07.2011 2103/4275 «О преподавании учебного предмета «Математика» в общеобразовательных учреждениях Челябинской области в 2011/2012 учебном году».
Приложение к письму МО и Н Челябинской области №74/5136 от 16.07.2012 г. «О преподавании учебного предмета «Математика» в общеобразовательных учреждениях Челябинской области в 2012/2013 учебном году».
Алгебра и начала математического анализа. Программы общеобразовательных учреждений. 10-11 классы. Для учителей общеобразовательных учреждений. / [ составитель Т.А. Бурмистрова.]. – М.: Просвещение, 2011.
Итоговый аналитический отчет о результатах ЕГЭ 2012 года Федерального института педагогических измерений.
Положение о рабочей программе педагога МОУ СОШ №147 от 29.08.2009 №211/1.
Приказ МО и Н Челябинской области от 16.06.2011 №04-997 «Об утверждении областного базисного учебного плана общеобразовательных учреждений Челябинской области на 2011/2012 учебный год».
Школьный учебный план на 2012-2013 учебный год.
Цели изучения алгебры и начал анализа в 10 классе:
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
воспитание средствами математики культуры личности: отношения к математике как части общечеловеческой культуры: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.
Цель индивидуально-групповых занятий по алгебре и началам математического анализа:
на основе коррекции базовых математических знаний учащихся совершенствовать математическую культуру и творческие способности учащихся.
Преподавание индивидуально-групповых занятий решает следующие задачи:
Формирование у учащихся целостного представления о теме, ее значения в разделе математики, связи с другими темами.
Формирование поисково-исследовательского метода.
Формирование аналитического мышления, развитие памяти, кругозора, умение преодолевать трудности при решении более сложных задач.
Осуществление работы с дополнительной литературой.
Акцентировать внимание учащихся на единых требованиях к правилам оформления различных видов заданий, включаемых в итоговую аттестацию за курс полной общеобразовательной средней школы;
Расширить математические представления учащихся по определённым темам, включённым в программы вступительных экзаменов в другие типы учебных заведений.
Умения и навыки учащихся, формируемые индивидуально-групповыми занятиями:
навык самостоятельной работы с таблицами и справочной литературой;
составление алгоритмов решения типичных задач;
умения решать нестандартные математические задачи.
Формы организации учебных занятий:
Формы проведения занятий индивидуально-групповых занятий включают в себя закрепление ранее изученного учебного материала, индивидуальные и групповые консультации, практические работы. Преподавание практикума строится на основе расширения и углубления базового курса алгебры и начал анализа, который ведется на оба модуля (универсальный и социально-правовой), кроме того, рассматриваются некоторые дополнительные вопросы, не входящие в базовый курс.
Преподавание практикума строится на основе обучения методам и приемам математических задач, требующих высокой логической и операционной культуры, развивающих научно-теоретическое и алгоритмическое мышление учащихся. Большое внимание уделяется учащимся, которые на недостаточно высоком уровне, владеют предметными компетенциями по алгебре. Ученикам, имеющим высокий уровень знаний и умений, предлагаются индивидуальные задания. Занятия практикума строятся с учётом индивидуальных особенностей обучающихся, их темпа восприятия и уровня усвоения материала.
Систематическое повторение способствует более целостному осмыслению изученного материала, поскольку целенаправленное обращение к изученным ранее темам позволяет учащимся встраивать новые понятия в систему уже освоенных знаний.
Контроль и система оценивания: Текущий контроль уровня усвоения материала осуществляется на каждом занятии по результатам выполнения учащимися самостоятельных, практических и тестовых работ.
Цели изучения индивидуально-групповых занятий по алгебре и началам математического анализа в 10 классе представлены в таблице:
Глава
|
Цели изучения главы
|
Повторение алгебры основной школы
|
Обобщить и систематизировать знания и умения учащихся по основным вопросам алгебры основной школы;
Провести подготовку к дальнейшему изучению алгебры и начал анализа 10 класса.
|
Степень с действительным показателем
|
Обобщить и систематизировать знания о действительных числах;
сформировать понятие степени с действительным показателем;
научить применять определения арифметического корня и степени, а также их свойства при выполнении вычислений и преобразований выражений.
|
Степенная функция
|
Обобщить и систематизировать известные из курса алгебры основной школы свойства функции;
изучить свойства степенных функций и научить применять их при решении уравнений и неравенств;
сформировать понятие равносильности уравнений, неравенств, систем уравнений и неравенств.
|
Показательная функция
|
Изучить свойства показательной функции;
Научить решать показательные уравнения и неравенства, системы показательных уравнений.
|
Логарифмическая функция
|
Сформировать понятие логарифма числа;
Научить применять свойства логарифмов при решении уравнений;
Изучить свойства логарифмической функции;
Научить применять ее свойства при решении логарифмических уравнений и неравенств.
|
Тригонометрические формулы
|
Сформировать понятия синуса, косинуса, тангенса, котангенса числа;
Научить применять формулы тригонометрии для вычисления тригонометрических функций и выполнения преобразований тригонометрических выражений;
Научить решать простейшие тригонометрические уравнения sin x=a, cos x =a при а=1;-1;0.
|
Тригонометрические уравнения
|
Сформировать умение решать простейшие тригонометрические уравнения;
Ознакомить с некоторыми приемами решения тригонометрических уравнений.
|
Программа индивидуально-групповых занятий по алгебре и началам математического анализа содержит следующие главы:
Глава
|
Содержание программы
|
Повторение алгебры основной школы
|
Решение уравнений и неравенств. Начала статистики. Функции, их свойства и графики.
|
Степень с действительным показателем
|
Бесконечно убывающая геометрическая прогрессия. Арифметический корень натуральной степени. Степень с натуральным и действительным показателями.
|
Степенная функция
|
Степенная функция, ее свойства и график. Асимптоты. Дробно-линейная функция. Иррациональные уравнения. Иррациональные неравенства. Системы иррациональных уравнений и неравенств.
|
Показательная функция
|
Показательные уравнения. Показательные неравенства. Системы показательных уравнений и неравенств.
|
Логарифмическая функция
|
Логарифмы. Свойства логарифмов. Формула перехода. Логарифмическая функция, ее свойства и график. Логарифмические уравнения. Логарифмические неравенства. Системы логарифмических уравнений и неравенств.
|
Тригонометрические формулы
|
Определение синуса, косинуса и тангенса угла. Зависимость между синусом, косинусом и тангенсом одного и того же угла. Тригонометрические тождества. 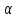 . Формулы сложения. Синус, косинус и тангенс двойного угла. Синус, косинус и тангенс половинного угла. Формулы приведения. Сумма и разность синусов. Сумма и разность косинусов. . Формулы сложения. Синус, косинус и тангенс двойного угла. Синус, косинус и тангенс половинного угла. Формулы приведения. Сумма и разность синусов. Сумма и разность косинусов.
|
Тригонометрические уравнения
|
Уравнения cos x =a, sin x =a, tg x=a.Тригонометрические уравнения, сводящиеся к квадратным. Однородные и линейные уравнения. Методы замены неизвестного и разложения на множители. Метод оценки левой и правой частей тригонометрического уравнения.
|
Количество часов по школьному учебному плану – 1 час в неделю, т.е.35 часов в году (учтено 35 учебных недели).
Количество часов по рабочей программе – 1 час в неделю, т.е. 35 часов в году (учтено 35 учебных недели).
Рабочая программа индивидуально-групповых занятий по алгебре и началам математического анализа составлена на основе «Примерной программы среднего (полного) общего образования по математике» (алгебра и начала математического анализа), с учетом требований федерального компонента государственного стандарта общего образования и на основе авторских рекомендаций Ю.М. Колягина и др., представленных в пособии: «Алгебра и начала математического анализа. Программы общеобразовательных учреждений. 10-11 классы. Для учителей общеобразовательных учреждений. / [ составитель Т.А. Бурмистрова.]. – М.: Просвещение, 2011» и сборника «Факультативные курсы. Сборник №2, Часть 1. – М.: Просвещение, 1990».Также учтены методические рекомендации к составлению рабочей программы и календарно-тематического планирования к учебно-методическому комплекту по алгебре и началам математического анализа Ю.М. Колягина и др., представленные в пособии: «Алгебра и начала анализа. 10-11 классы: рабочие программы по учебникам Ю.М. Колягина и др.: базовый и профильный уровни / авт.-сост. Н.А. Ким.- Волгоград: Учитель, 2011».
№ п/п
|
Содержание учебного материала
|
Фактическое распределение учебного времени (35 учебных недели)
|
1.
|
Повторение алгебры основной школы
|
3
|
2.
|
Степень с действительным показателем
|
3
|
3.
|
Степенная функция
|
5
|
4.
|
Показательная функция
|
3
|
5.
|
Логарифмическая функция
|
6
|
6.
|
Тригонометрические формулы
|
8
|
7.
|
Тригонометрические уравнения
|
7
|
ТРЕБОВАНИЯ К МАТЕМАТИЧЕСКОЙ ПОДГОТОВКЕ УЧАЩИХСЯ 10 КЛАССОВ
В результате изучения алгебры и начала анализа на базовом уровне ученик должен
знать/понимать:
- значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов и иссле�дованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и раз�вития математической науки; историю развития понятия числа, создания математического ана�лиза;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
- вероятностный характер различных процессов окружающего мира.
уметь
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
Функции и графики
уметь
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций;
описывать по графику поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков;
Начала математического анализа
уметь
исследовать в простейших случаях функции на монотонность
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
Уравнения и неравенства
уметь
решать рациональные, показательные и логарифмические уравнения и неравенства,
составлять уравнения и неравенства по условию задачи;
использовать для приближенного решения уравнений и неравенств графический метод;
изображать на координатной плоскости множества решений простейших уравнений и их систем;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
УЧЕБНО-ДИДАКТИЧЕСКОЕ СОПРОВОЖДЕНИЕ:
Учебник: Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений : базовый и проф. уровни /[ Ю.М. Колягин, М.В.Ткачева, Н.Е. Федорова, М.И. Шабунин]; под ред. А.Б. Жижченко. – М.: Просвещение, 2010.
Методические пособия для учителя:
1.Изучение алгебры и начал математического анализа в 10 классе: кн. Для учителя /Н.Е. Федорова, М.В. Ткачева. – М.: Просвещение, 2008-2010.
2.Алгебра и начала математического анализа: дидакт. материалы для 10 кл. общеобразоват. учреждений: профил. уровень /[М.И. Шабунин, М.В. Ткачева, Н.Е. Федорова, О.Н. Доброва]. –М.: Просвещение,2008.
3. Алгебра и начала математического анализа: дидакт. материалы для 10 кл. общеобразоват. учреждений: базов. уровень /[М.И. Шабунин, М.В. Ткачева, Н.Е. Федорова, О.Н. Доброва]. –М.: Просвещение,2008.
4. Алгебра и начала математического анализа. Тематические тесты. 10 класс: базовый и профил. уровни /М.В. Ткачева, Н.Е. Федорова.- М.: Просвещение, 2009.
5. Задачи по алгебре и началам анализа: Пособие для учащихся 10-11 кл. общеобразоват. учреждений / С.М. Саакян, А.М. Гольдман, Д.В. Денисов. – М.: Просвещение, 2011.
6.Галицкий М.Л. и др. Углубленное изучение алгебры и математического анализа: методические рекомендации и дидактические материалы: Пособие для учителя – М.: Просвещение, 1997-2005.
7.Звавич Л.И. и др. Алгебра и начала анализа. 8-11 класс.: Пособие для школ и классов с углубленным изучением математики – М.: Дрофа, 1998 – 2007.
8.Функции и графики в 8-11 классах./ Е.В. Ромашкова.- М.: ИЛЕКСА, 2011.
9. Алгебра. Базовый курс с решениями и указаниями (ЕГЭ, олимпиады, экзамены в вуз). Учебно-методическое пособие Н.Д. Золотарева, Ю.А. Попов, Н.Л. Семендяева, М.В. Федотов.- М.: Фойлис, 2010.
10. Математика. Сборник задач по базовому курсу ( ЕГЭ, олимпиады, экзамены в вуз). Учебно-методическое пособие /Н.Д. Золотарева, Ю.А. Попов, Н.Л. Семендяева, М.В. Федотов.- М.: Фойлис, 2010.
11.Алгебра. Углубленный курс с решениями и указаниями: учебно-методическое пособие /Н.Д. Золотарева, Ю.А. Попов, В.В. Сазонов, Н.Л. Семендяева, М.В. Федотов.; Под ред. М.В. Федотова.- М.: Издательство Московского университета, 2011.
12.Тригонометрия:задачи решения: Учебно-практическое пособие. /Г.И. Просветов. - М.: Издательство «Альфа-Пресс», 2010.
13.Степени, корни и логарифмы: задачи и решения: Учебно-практическое пособие./ Г.И. Просветов.- М.: Издательство «Альфа-Пресс», 2010.
14.Графики функций: задачи и решения: Учебно-практическое пособие.- М.: Издательство «Альфа-Пресс», 2010.
15. Алгебра и начала анализа. 10 класс: поурочные планы по учебнику Ш.А. Алимова и др. 1 полугодие, 2 полугодие /авт.-сост. Г.И. Григорьева.- Волгоград: учитель, 2008.
Дидактические материалы:
1. Алгебра и начала математического анализа: дидакт. материалы для 10 кл. общеобразоват. учреждений: базов. уровень /[М.И. Шабунин, М.В. Ткачева, Н.Е. Федорова, О.Н. Доброва]. –М.: Просвещение,2008.
2. Алгебра и начала математического анализа. Тематические тесты. 10 класс: базовый и профил. уровни /М.В. Ткачева, Н.Е. Федорова.- М.: Просвещение, 2009.
3.Самостоятельные и контрольные работы по алгебре и началам анализа для 10-11 классов. / А.П.Ершова, В.В. Голобородько. – М.: Илекса, 2011.
4. Дидактические материалы по алгебре для 10-11 классов./ Б.Г. Зив, В.А. Гольдич. – СПб.: «Петроглиф», «Виктория плюс», 2010.
5. Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубл. изучением математики./ Л.И. Звавич, Л.Я. Шляпочник, М.В. Чинкина.- М.: Дрофа, 1999-2010.
6.Алгебра и начала математического анализа. 10, 11 классы . Контрольные работы в НОВОМ формате: [учебное пособие] /Ю.П. Дудницын, А.В. Семенов; [под общ. ред. А.В. Семенова]; Московский центр непрерывного математического образования. – М.: Интеллект-Центр, 2011.
7. Математика. 10-й класс. Промежуточная аттестация в форме ЕГЭ. /Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова. - Ростов-на-Дону: Легион, 2012.
Инструментарий по отслеживанию результатов:
1. Алгебра и начала математического анализа: дидакт. материалы для 10 кл. общеобразоват. учреждений: базов. уровень /[М.И. Шабунин, М.В. Ткачева, Н.Е. Федорова, О.Н. Доброва]. –М.: Просвещение,2008.
2. Алгебра и начала математического анализа. Тематические тесты. 10 класс: базовый и профил. уровни /М.В. Ткачева, Н.Е. Федорова.- М.: Просвещение, 2009.
3. Дидактические материалы по алгебре для 10-11 классов./ Б.Г. Зив, В.А. Гольдич. – СПб.: «Петроглиф», «Виктория плюс», 2010.
4. Потапов М.К. Алгебра и начала анализа: дидактические материалы для 10,11 классов/ М.К. Потапов, А.В. Шевкин – М.: Просвещение, 2005-2008.
5.Алгебра и начала математического анализа. 10-11 классы. Обучающие контрольные работы. /П.И. Самсонов М.: Илекса, 2011.
6.Алгебра: профильный уровень: 10-11 классы: тематические и итоговые контрольные работы: дидактические материалы / [Н.Н. Гусева, Е.С. Федотова и др.].- М.: Вентана-Граф, 2011.
7. Тестовые материалы для оценки качества обучения. Алгебра и начала анализа. 10-11 класс. Учебное пособие /Л.Б. Крайнева; под общей редакцией А.О. Татура; Московский центр качества образования.- М.: «Интеллект-Центр».2012.
Цифровые образовательные ресурсы:
Уроки алгебры.10-11 классы. - М.: ООО «Кирилл и Мефодий», 2009.
Алгебра и начала анализа. – М.: Просвещение-МЕДИА, 2009.
Открытая математика. Функции и графики. – М.: Физикон, 2008.
Открытая математика. Алгебра. – М.: Физикон, 2008.
Образовательная коллекция. Алгебра. 7-11 классы.- М: Фирма «1С», 2010.
Интернет-ресурсы представлены в таблице:
№ п/п
|
Название
|
Электронный адрес
|
1.
|
МО и Н РФ
|
www.mon.gov.ru
|
2.
|
Российский образовательный портал
|
www.school.edu.ru
|
3.
|
Федеральный институт педагогических измерений
|
www.fipi.ru
|
4.
|
Московский институт открытого образования
|
www.mioo.ru
|
5.
|
Интернет-поддержка учителей математики
|
www.math.ru
|
6.
|
Сеть творческих учителей
|
www.it-n.ru
|
7.
|
Сайт журнала «Математика в школе»
|
matematika@schoolpress.ru
|
8.
|
Единая коллекция образовательных ресурсов
|
http: / school.collection.informatika.ru
|
9.
|
Челябинский институт переподготовки и повышения квалификации работников образования
|
www.ipk74.ru
|
10.
|
Челябинский городской методический центр
|
www.chel-edu.ru
|
11.
|
Журнал «Математика» (приложение к газете «Первое сентября»)
|
www.mat.1september.ru
|
Дополнительная литература для учащихся:
Алгебра в таблицах. 7-11 классы. Справочное пособие. / авт.-сост. Л.И. Звавич, А.Р.Рязановский. –М.: Дрофа, 2011.
Календарно-тематическое планирование индивидуально-групповых занятий по алгебре и началам математического анализа. 10 класс.
(1 час в неделю. 35 часов в учебном году)
№ п/п урока
|
Дата
|
Содержание учебного материала
|
Требования к результатам обучения
|
Примечание
|
Повторение алгебры основной школы. (3 часа)
|
1.
|
|
Решение уравнений и неравенств.
|
Уметь:
Решать линейные уравнения, системы двух линейных уравнений и несложные нелинейные системы.
Решать линейные неравенства с одной переменной и их системы.
Решать квадратные уравнения.
Решать квадратные неравенства, их системы.
|
|
2.
|
|
Начала статистики.
|
Уметь:
Извлекать информацию, представленную в таблицах, на диаграммах, графиках;
Составлять таблицы, строить диаграммы и графики;
Вычислять средние значения результатов измерений.
Использовать приобретенные знания и умения в практической деятельности повседневной жизни для:
Выстраивания аргументации при доказательстве (в форме монолога и диалога);
Записи математических утверждений, доказательств;
Анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
Понимания статистических утверждений.
|
|
3.
|
|
Функции, их свойства и графики.
|
Уметь:
Находить значения функции, заданной формулой, таблицей, графиком по ее аргументу;
Находить значение аргумента по значению функции, заданной графиком или таблицей;
Определять свойства функции по ее графику;
Описывать свойства изученных функций, строить их графики.
|
|
Глава 4. Степень с действительным показателем. (3 часа)
|
4.
|
|
Бесконечно убывающая геометрическая прогрессия.
|
Уметь:
Распознавать бесконечно убывающую геометрическую прогрессию;
Решать задачи с применением формулы общего члена и суммы нескольких первых членов.
|
|
5.
|
|
Арифметический корень натуральной степени.
|
Уметь:
Проводить по известным формулам и правилам преобразования буквенных выражений, включающих радикалы;
Вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Практических расчетов по формулам, включая формулы, содержащие радикалы, используя при необходимости справочные материалы и простейшие вычислительные устройства.
|
|
6.
|
|
Степень с рациональным действительным показателями.
|
Уметь:
Проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени;
Вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Практических расчетов по формулам, включая формулы, содержащие степени, используя при необходимости справочные материалы и простейшие вычислительные устройства.
|
|
Глава 5.Степенная функция. (5 часов)
|
7.
|
|
Степенная функция.
|
Уметь:
Находить значения функции, заданной формулой, таблицей, графиком по ее аргументу;
Находить значение аргумента по значению функции, заданной графиком или таблицей;
Определять свойства функции по ее графику;
Описывать свойства изученных функций, строить их графики
|
|
8.
|
|
Нахождение асимптот. График дробно-линейной функции.
|
Уметь:
Находить значения функции, заданной формулой, таблицей, графиком по ее аргументу;
Находить значение аргумента по значению функции, заданной графиком или таблицей;
Определять свойства функции по ее графику;
Описывать свойства изученных функций, строить их графики
|
|
9.
|
|
Иррациональные уравнения.
|
Уметь:
Решать простейшие иррациональные уравнения, их системы.
|
|
10.
|
|
Иррациональные неравенства.
|
Уметь:
Решать простейшие иррациональные неравенства, их системы.
|
|
11.
|
|
Системы иррациональных уравнений и неравенств.
|
Уметь:
Решать простейшие иррациональные уравнения, их системы.
|
|
Глава 6. Показательная функция. (3 часа)
|
12.
|
|
Показательные уравнения.
|
Уметь:
Решать показательные уравнения, их системы.
|
|
13.
|
|
Показательные неравенства.
|
Уметь:
|
|
14.
|
|
Системы показательных уравнений и неравенств.
|
Уметь:
Решать показательные уравнения, их системы.
Решать показательные неравенства, их системы.
|
|
Глава 7. Логарифмическая функция. (6 часов)
|
15.
|
|
Логарифма числа.
|
Уметь:
Проводить по известным формулам и правилам преобразования буквенных выражений, включающих логарифмы;
Вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Практических расчетов по формулам, включая формулы, содержащие логарифмы, используя при необходимости справочные материалы и простейшие вычислительные устройства
|
|
16.
|
|
Свойства логарифмов.
|
Уметь:
Проводить по известным формулам и правилам преобразования буквенных выражений, включающих логарифмы;
Вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Практических расчетов по формулам, включая формулы, содержащие логарифмы, используя при необходимости справочные материалы и простейшие вычислительные устройства
|
|
17.
|
|
Формула перехода.
|
Уметь:
Проводить по известным формулам и правилам преобразования буквенных выражений, включающих логарифмы;
Вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Практических расчетов по формулам, включая формулы, содержащие логарифмы, используя при необходимости справочные материалы и простейшие вычислительные устройства.
|
|
18.
|
|
Логарифмические уравнения.
|
Уметь:
Решать логарифмические уравнения.
|
|
19.
|
|
Логарифмические неравенства.
|
Уметь:
Решать логарифмические неравенства.
|
|
20.
|
|
Системы логарифмических уравнений и неравенств.
|
Уметь:
Решать логарифмические уравнения и неравенства.
|
|
Глава 8. Тригонометрические формулы.(8 часов)
|
21.
|
|
Определение синуса, косинуса, тангенса и котангенса угла.
|
Знать:
Определение синуса и косинуса угла;
Определение тангенса и котангенса.
|
|
22.
|
|
Зависимость между синусом, косинусом и тангенсом одного и того же угла.
|
Уметь:
Проводить по известным формулам и правилам преобразования буквенных выражений. Включающих тригонометрические функции;
Вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
|
|
23.
|
|
Тригонометрические тождества.
|
Уметь:
Проводить по известным формулам и правилам преобразования буквенных выражений. Включающих тригонометрические функции;
Вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Практических расчетов по формулам, включая формулы, содержащие тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
|
|
24.
|
|
Формулы сложения.
|
Уметь:
Проводить по известным формулам и правилам преобразования буквенных выражений. Включающих тригонометрические функции;
Вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Практических расчетов по формулам, включая формулы, содержащие тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
|
|
25.
|
|
Синус, косинус и тангенс двойного угла.
|
Уметь:
Проводить по известным формулам и правилам преобразования буквенных выражений. Включающих тригонометрические функции;
Вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Практических расчетов по формулам, включая формулы, содержащие тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
|
|
26.
|
|
Синус, косинус и тангенс половинного угла.
|
Уметь:
Проводить по известным формулам и правилам преобразования буквенных выражений. Включающих тригонометрические функции;
Вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Практических расчетов по формулам, включая формулы, содержащие тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
|
|
27.
|
|
Формулы приведения.
|
Уметь:
Проводить по известным формулам и правилам преобразования буквенных выражений. Включающих тригонометрические функции;
Вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Практических расчетов по формулам, включая формулы, содержащие тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
|
|
77.
|
|
Сумма и разность синусов.
Сумма и разность косинусов.
|
Уметь:
Проводить по известным формулам и правилам преобразования буквенных выражений. Включающих тригонометрические функции;
Вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Практических расчетов по формулам, включая формулы, содержащие тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
|
|
Глава 9. Тригонометрические уравнения.(7 часов)
|
29.
|
|
Уравнение cos x=a и sin x=a.
|
Уметь:
Решать простейшие тригонометрические уравнения.
|
|
30.
|
|
Уравнение tg x =a и ctg x=a. .
|
Уметь:
Решать простейшие тригонометрические уравнения.
|
|
31.
|
|
Уравнения, сводящиеся к квадратным.
|
Уметь:
Решать тригонометрические уравнения.
|
|
32.
|
|
Уравнения, однородные относительно синуса и косинуса.
|
Уметь:
Решать тригонометрические уравнения.
|
|
33.
|
|
Уравнения, линейные относительно синуса и косинуса.
|
Уметь:
Решать тригонометрические уравнения.
|
|
34.
|
|
Решение уравнений методом замены переменной.
|
Уметь:
Решать тригонометрические уравнения.
|
|
35.
|
|
Метод оценки левой и правой частей тригонометрического уравнения.
|
Уметь:
Решать тригонометрические уравнения.
|
| |
|
|
 Скачать 303.39 Kb.
Скачать 303.39 Kb.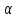 . Формулы сложения. Синус, косинус и тангенс двойного угла. Синус, косинус и тангенс половинного угла. Формулы приведения. Сумма и разность синусов. Сумма и разность косинусов.
. Формулы сложения. Синус, косинус и тангенс двойного угла. Синус, косинус и тангенс половинного угла. Формулы приведения. Сумма и разность синусов. Сумма и разность косинусов.