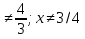Самостоятельная работа по группам. Учащиеся по группам выполняют задание 5 минут
 Скачать 30.49 Kb. Скачать 30.49 Kb.
|
            Муниципальное общеобразовательное учреждение Муниципальное общеобразовательное учреждение«Новоурусовская средняя общеобразовательная школа » Красноярского района Астраханской области. Урок алгебры в 9 классе по теме «Неравенства второй степени с одной переменной» Учитель математики Искабулова С.Х. 2012 – 2013 уч.год Тема урока: «Неравенства второй степени с одной переменной» Урок изучения новых знаний Цель урока: 1. Ознакомить учащихся с решением неравенств второй степени с одной переменной, обеспечить усвоение алгоритма решения таких неравенств; 2.Развивать логическое мышление, память, речь, внимание. 3. Воспитывать интерес к математике, графическую культуру. Оборудование: компьютер, экран, проектор. Ход урока.
а) Разбор вопросов по д/ з ( анализ нерешенных пунктов) б) Что является графиком функции у = ах2 +вх +с? От чего зависит направление ветвей параболы? в) Самостоятельная работа по группам. Учащиеся по группам выполняют задание 5 минут. Результаты сверить по таблице на экране, ошибки разобрать. Задание: Решите уравнение:
На экране слайды. Определение: Неравенства вида ах2 +вх +с>0 и ах2 +вх +с<0, где х- переменная, а,в,с- некоторые числа ( а  ), ),неравенствами второй степени с одной переменной. Алгоритм решения неравенства второй степени с одной переменной:
при а< 0 ветви вниз.
Если ≥ и ≤ , то «точки жирные» Если > и < , то « точки выколотые» С учетом направления ветвей строим параболу.
и в нижней полуплоскости при а< 0.
На доске разобрать примеры соответственно алгоритму. Пример 1. 5х2 + 9х – 2 < 0 5х2 + 9х – 2 = 0 а = 5 > 0 – вверх; Д = в2 - 4ас = 81 +40 = 121 = 112 ; Х1= 1/5; + + х х2 = -2. -2° 1/5° Ответ: (-2; 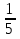 ) ) Акцентировать внимание на то, что: а)у трёхчлена два корня; б)на расстановку знаков, т.е. то, что ниже оси Ох – минус, то что выше оси Ох – плюс; в) ответ выбираем в соответствии со знаком неравенства. Пример 2. 3х2 – 11х – 4 > 0 + + Д = 169, х1 = 4, х2 = -  - -  ° 4 ° ° 4 ° Ответ: (- 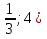 Пример 3. 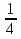 х2 +2х - 4> 0 х2 +2х - 4> 0а =  - ветви параболы вверх. - ветви параболы вверх.Д = 0, х= 8 + + + ° 8 Ответ: (-  ) U (8; +∞) ) U (8; +∞)Пример 4. Х2 – 3х+ 4> 0 а = 1 > 0- парабола ветвями вверх. Д = -7. Х Ответ: х – любое. В последнем примере акцентировать внимание на пункте 4 алгоритма.
№ 304(б,г) Ответы: б) (- 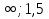 ) U (2; +∞) ) U (2; +∞)г) (- 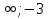 ) U (5; +∞) ) U (5; +∞)№ 306 (в,г) Ответ: в) [  ; 1 ; 1 ] ; г) (- ] ; г) (-  ] U [2; +∞) ] U [2; +∞)№ 308( а,д) Ответ: а) (- 4; 4), д) (-  ; 0) ; 0)
Повторить по пунктам алгоритм решения неравенств второй степени с одной переменной. Выставление оценок.
|
 = 0
= 0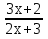 +
+  = -2
= -2 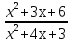 = 0
= 0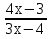 +
+  = 2
= 2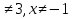

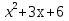 =0
=0