|
Ромб и квадрат, их свойства



 Учитель математики: Руденко О.Н. Учитель математики: Руденко О.Н.



 
 
 

 


М ОУ «Немёрзская ООШ» ОУ «Немёрзская ООШ»
2008 год
ТЕМА: «Ромб и квадрат, их свойства».
ЦЕЛИ:
Ввести понятия ромба и квадрата как частных видов параллелограмма;
Рассмотреть свойства ромба и квадрата и показать их применение в процессе решения задач;
Совершенствовать навыки решения задач.
Обогатить опыт использования компьютера через перенос ЗУНов, полученных на уроке геометрии:
развивать интеллектуальные умения: сравнение, анализ, синтез и способность к самооценке и самоанализу.
Дата проведения урока: 8 октября 2008 г.
Тип урока: комбинированный урок геометрии с использованием ИКТ;
Оборудование: цифровой проектор, компьютер, презентации PowerPoint: раздаточный материал с устными заданиями, теоретической самостоятельной работой.
Форма организации познавательной деятельности: фронтальная, индивидуальная.
Место проведения урока: кабинет математики;
Обучение ведется по учебнику Л. С. Атанасянa.
План урока:
Организационный этап.
2. Формирование новых знаний и способов действия.
3. Физкультминутка.
4. Применение знаний, формирование умений и навыков.
5. Теоретическая самостоятельная работа.
6. Подведение итогов.
7. Постановка домашнего задания.
Ход урока
Организационный этап (мотивация и постановка цели урока).
( Целью данного этапа урока является подготовка учащихся к восприятию нового материала.)
Проверка домашнего задания.
Определение, свойство и признак прямоугольника - 2 ученика у доски.
Тестирование на компьютере – 1 человек;
Остальные решают задачи на карточках:
Карточка №1.
Н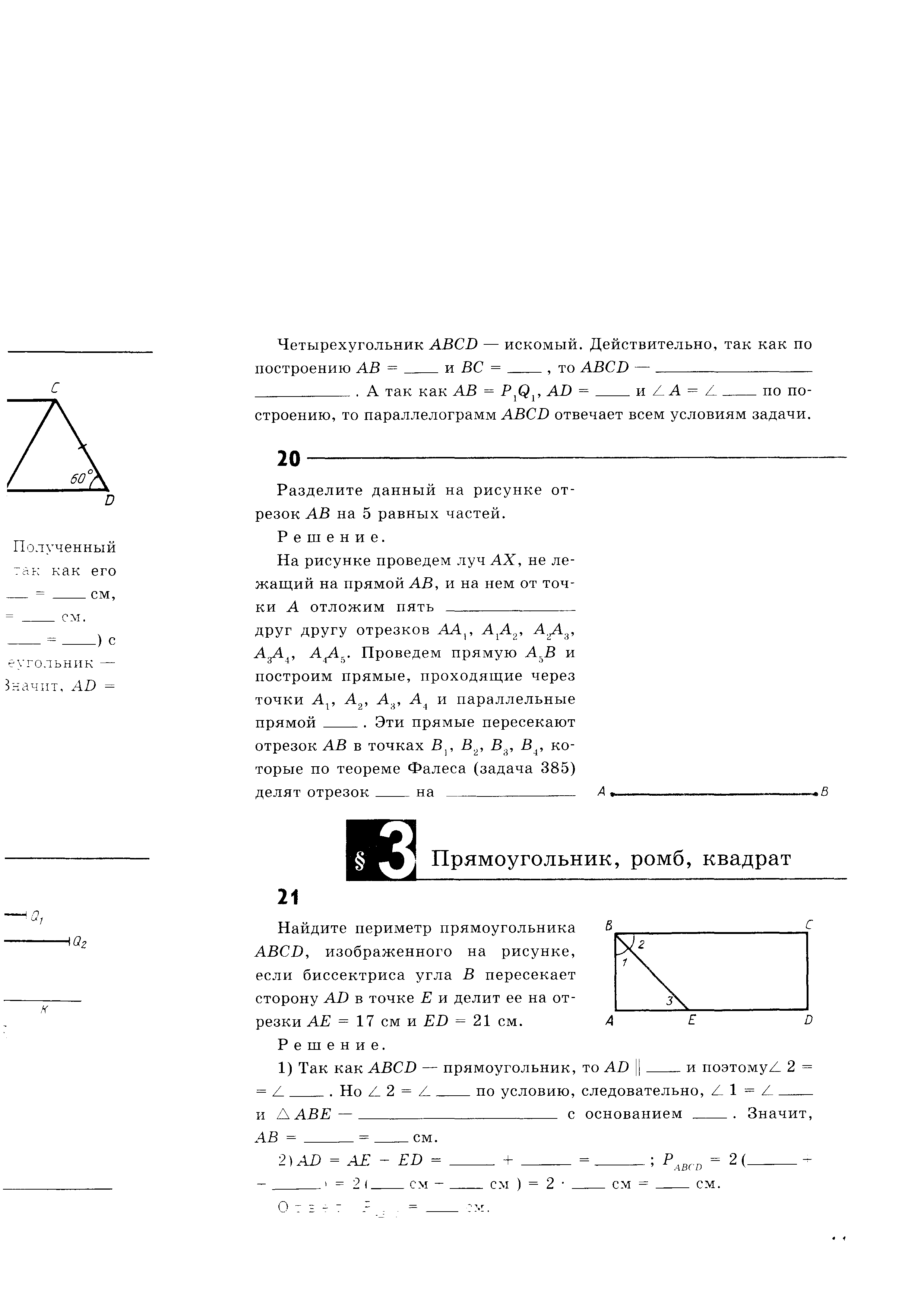 айдите периметр прямоугольника ABCD, изображённого на рисунке, если биссектриса угла В пересекает сторону AD в точке Е и делит её на отрезки АЕ = 17 см и ЕD = 21 см. айдите периметр прямоугольника ABCD, изображённого на рисунке, если биссектриса угла В пересекает сторону AD в точке Е и делит её на отрезки АЕ = 17 см и ЕD = 21 см.
Решение.
Так как ABCD – прямоугольник, то AD | | ____ и поэтому 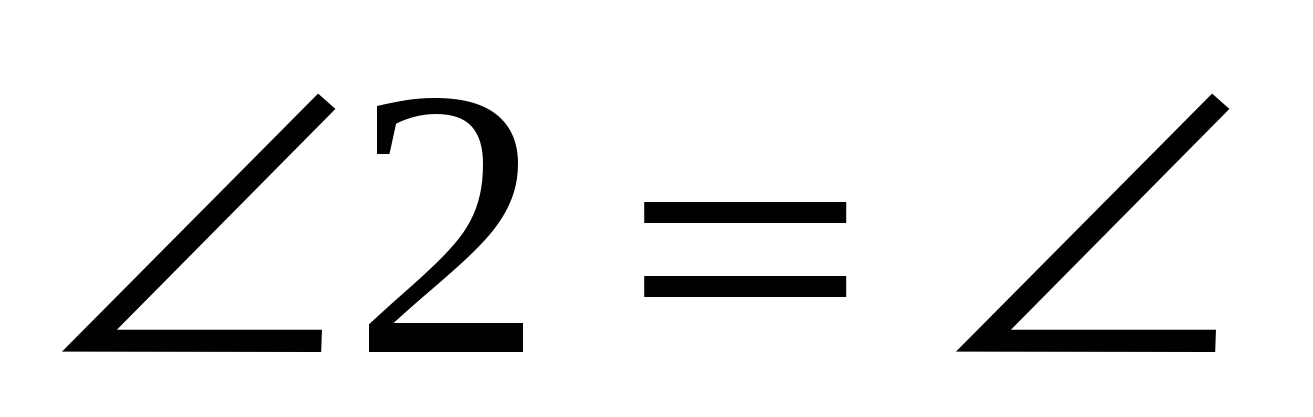 ___. ___.
Но 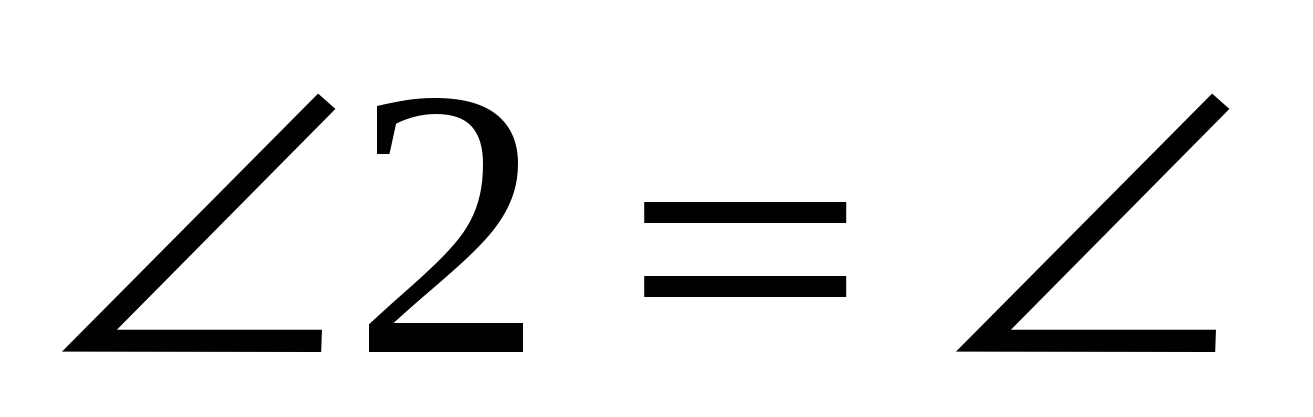 ___ по условию, следовательно, ___ по условию, следовательно, 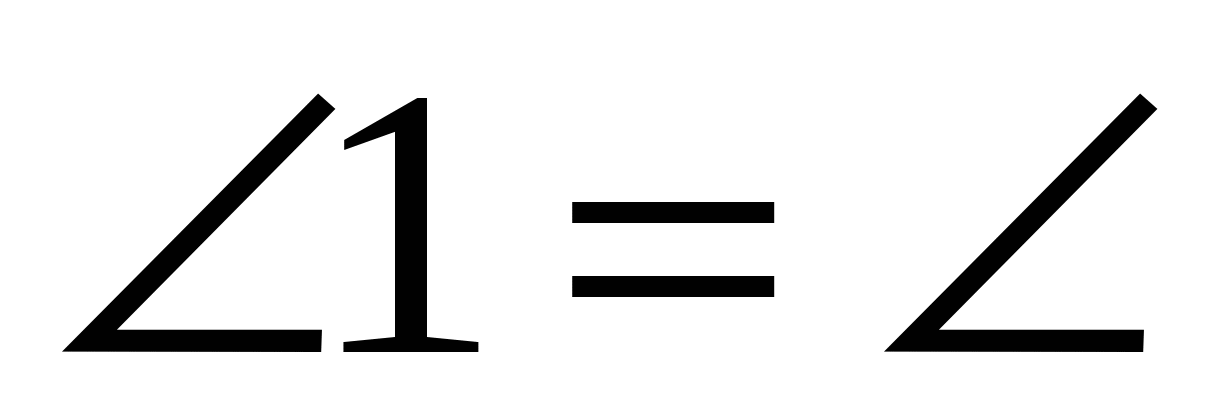 __ и ▲ABE - ____________ __ и ▲ABE - ____________
с основанием ___. Значит, АВ = ___ = ___ см.
2) AD = AE + ED = ___ + ___ = ___; PABCD = 2*(____ + ____) =
=2*(___ см + ___см) = 2*___ см = ___см.
Ответ: PABCD =___см.
Карточка №2.
В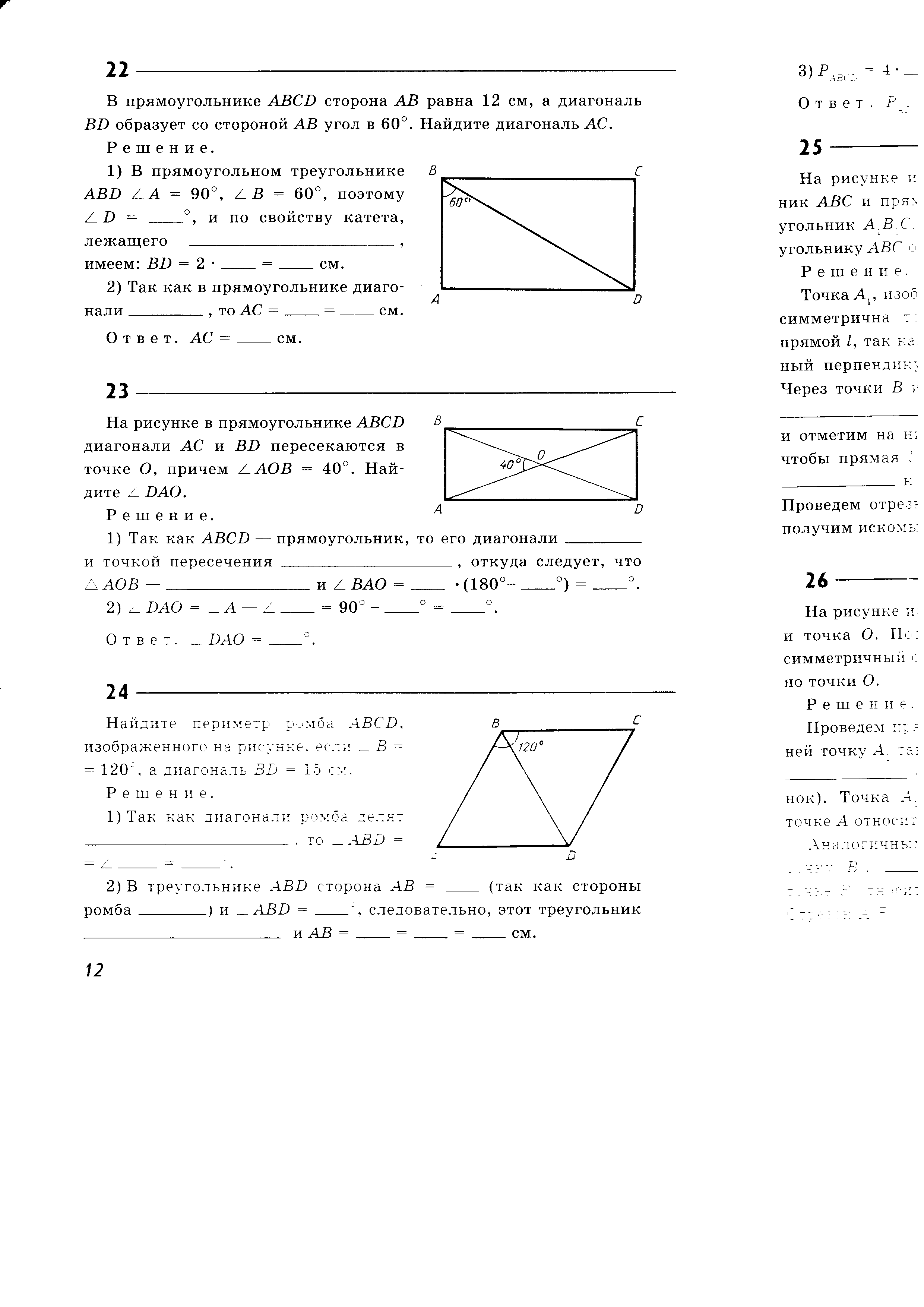 прямоугольнике ABCD сторона АВ = 12 см, а диагональ BD образует со стороной АВ угол в 60◦. Найдите диагональ АС. прямоугольнике ABCD сторона АВ = 12 см, а диагональ BD образует со стороной АВ угол в 60◦. Найдите диагональ АС.
Решение.
В прямоугольном треугольнике ABD 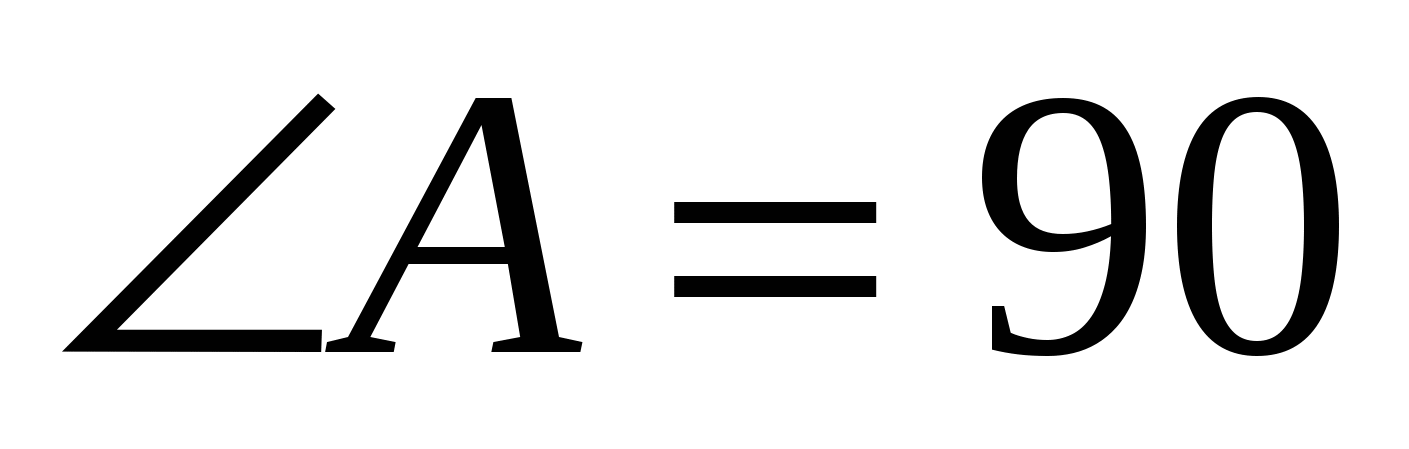 ◦, ◦, 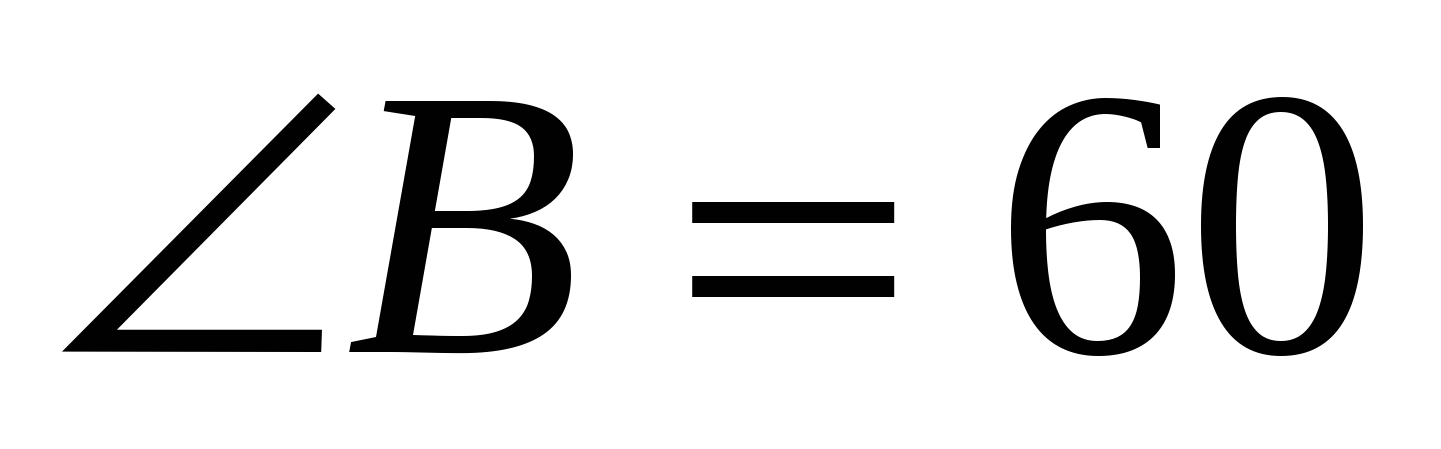 ◦, поэтому ◦, поэтому 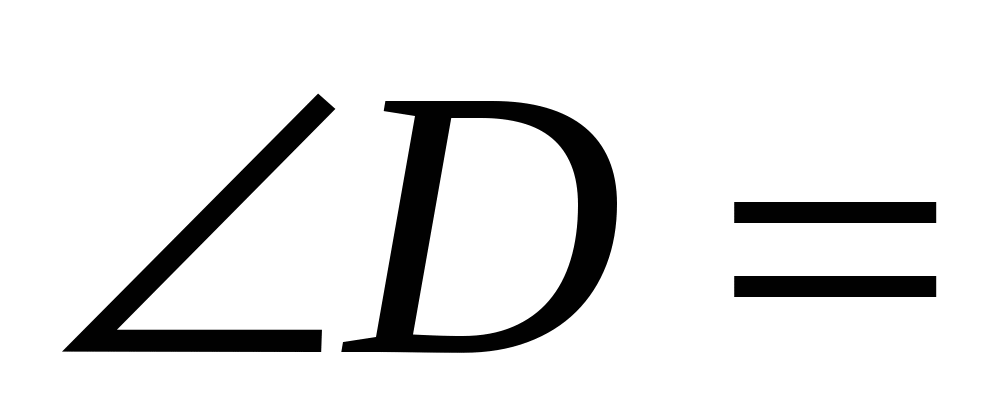 ___◦, и по свойству катета, лежащего _______________, имеем: BD = 2*__=__см. ___◦, и по свойству катета, лежащего _______________, имеем: BD = 2*__=__см.
Так как в прямоугольнике диагонали ______, то АС = ___=___см.
Ответ: АС= ___ см.
Карточка №3.
В прямоугольнике ABCD диагонали АС и BD пересекаются в точке О, причём
  ◦. Найдите ◦. Найдите 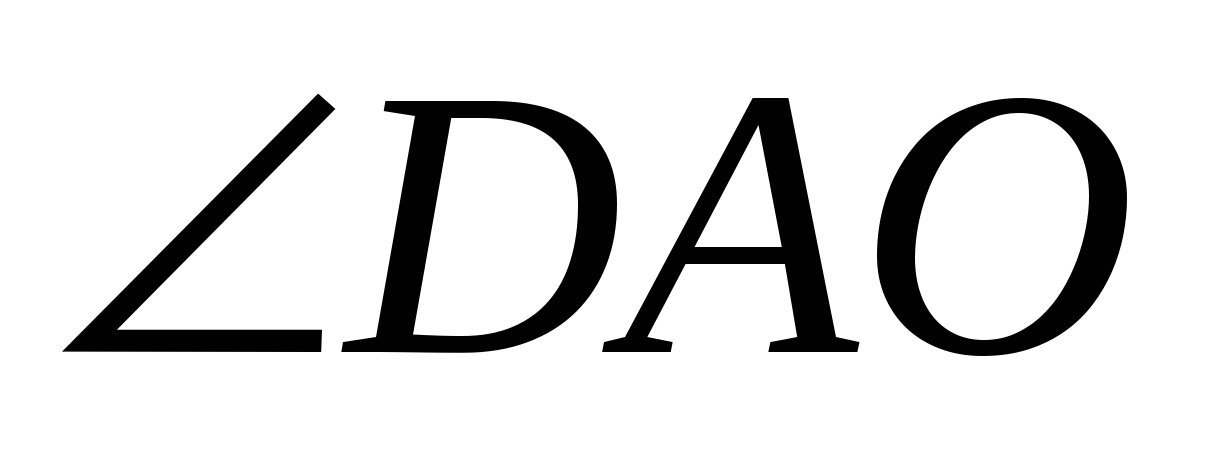 . .
Решение.
1) Так как ABCD – прямоугольник, то его диагонали ______ и точкой пересечения _____________________, откуда следует, что ▲АОВ - _________ и 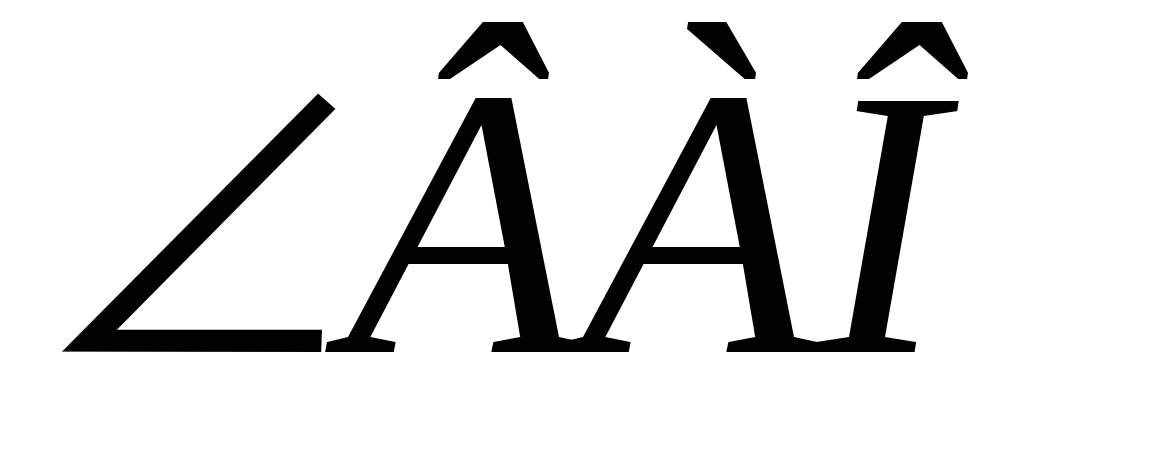 = ___*(180◦ - ___◦) = ___◦. = ___*(180◦ - ___◦) = ___◦.
2) 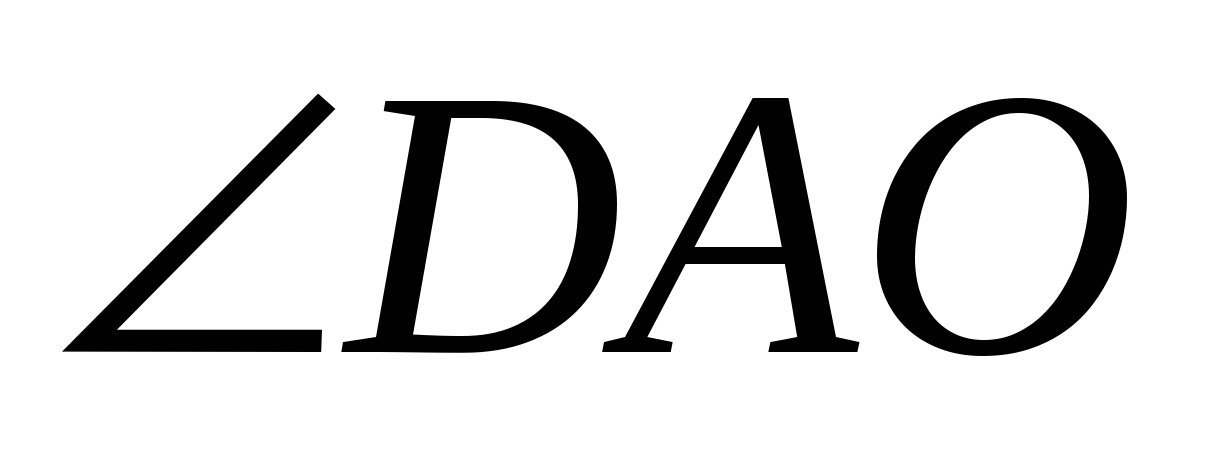 = = 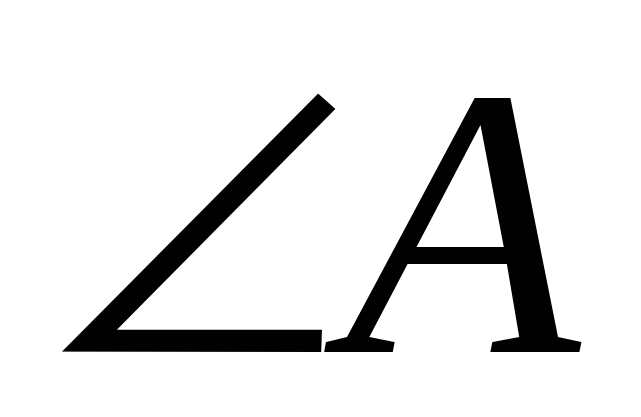 - - 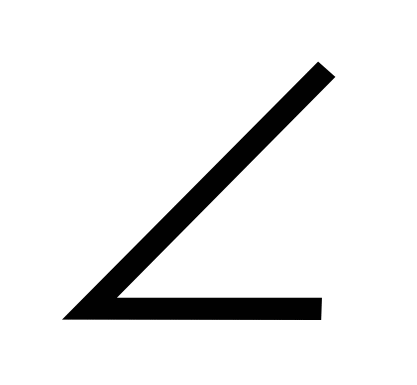 ___ = 90◦ - ___ ◦ = ___◦. ___ = 90◦ - ___ ◦ = ___◦.
Ответ: 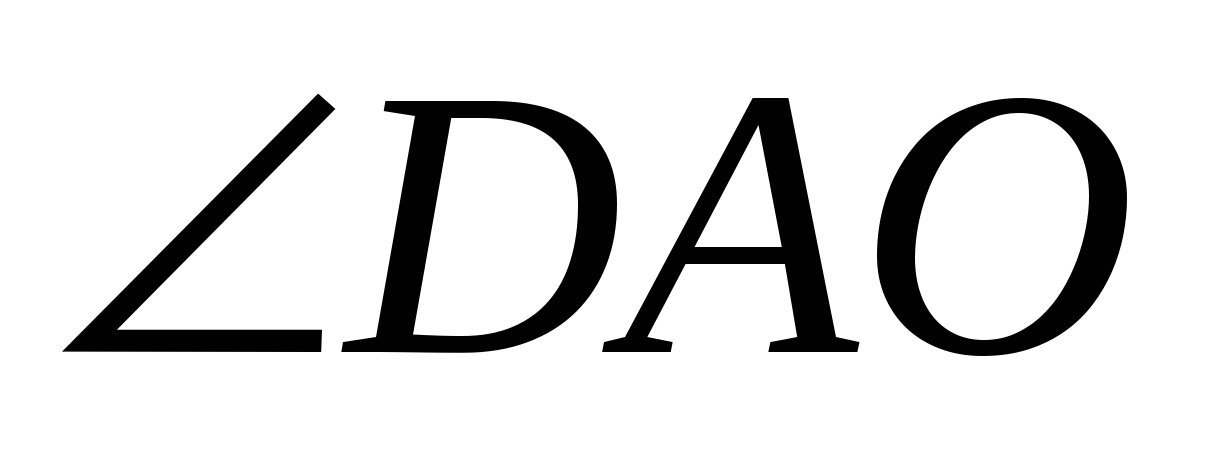 =___◦. =___◦.
2. Формирование новых знаний и способов действия.
( Цель этапа – введение понятия ромба и квадрата как частных видов параллелограмма; изучение свойств ромба и квадрата).

- Является ли параллелограммом четырёхугольник АВСD?
- Почему?
-Такой четырёхугольник является ещё одним частным случаем параллелограмма и называется ромбом.
Определение.
(Показ слайда)
Ромбом называется параллелограмм, у которого все стороны равны.
- Перечислите все свойства ромба как частного вида параллелограмма.
В ромбе все стороны равны. (по определению ромба)
В ромбе противоположные углы равны.
В ромбе противоположные стороны попарно параллельны.
В ромбе диагонали точкой пересечения делятся пополам.
- Выясните, каким ещё особым свойством обладают диагонали ромба, кроме того, что они точкой пересечения делятся пополам.
(Работа в парах с последующим обсуждением свойства диагоналей ромба).
Инструктаж к работе в парах по изучению свойства ромба.
Учитель инструктирует учащихся: о способе деятельности, о месте нахождения материала.
Задача пар:
прочитать доказательство;
определить основную идею доказательства;
выделить этапы и шаги доказательства;
4) дать обоснование каждому шагу
подготовить выступление от пары в защиту приведенного доказательства.
Самостоятельная работа в парах по изучению доказательства свойства ромба.
Публичная защита доказательства.
Одна из пар начинает свое выступление с формулировки свойства ромба.
(Идет активное обсуждение доказательства, в ходе которого с помощью вопросов учителя и учащихся обосновывается тот или иной вариант.)
Сравнение доказательства свойства ромба с презентацией учителя.
- Сравните своё доказательство свойства ромба с доказательством учителя.
(см. презентацию учителя)
Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
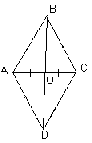
Дано: ABCD-ромб
Доказать: АС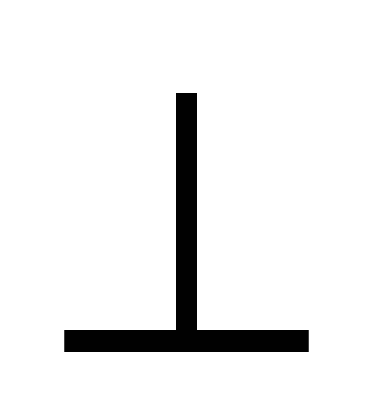 BD BD
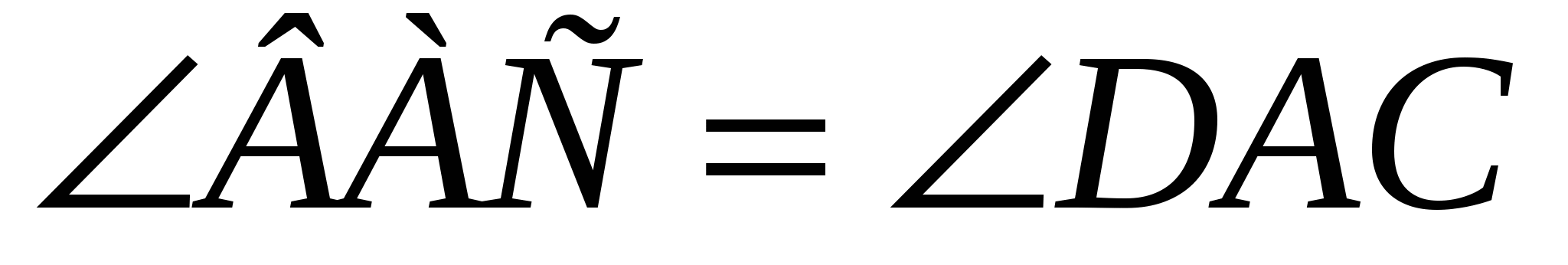
(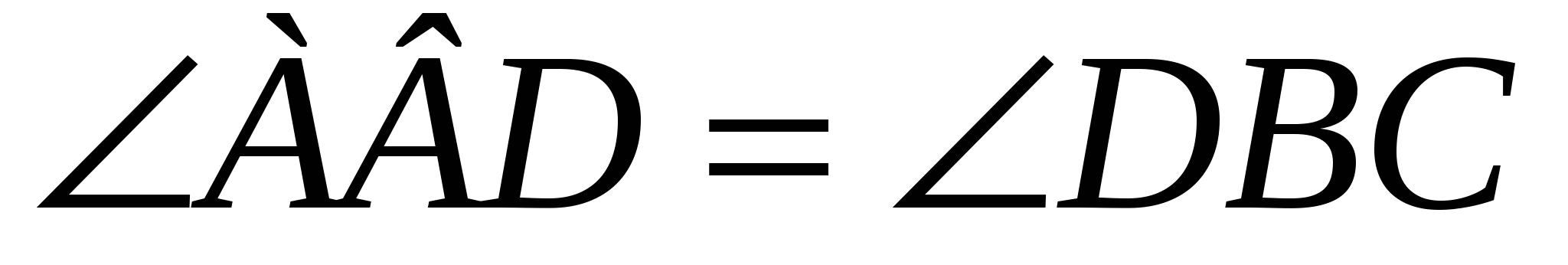 , , 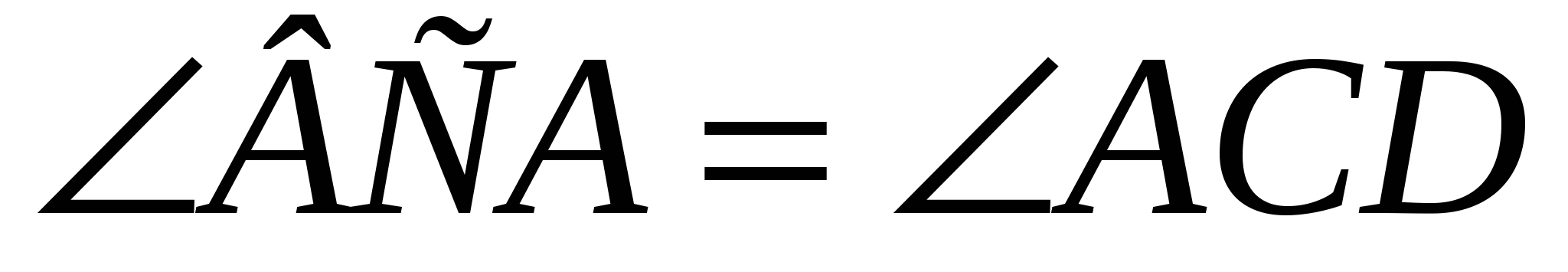 , , 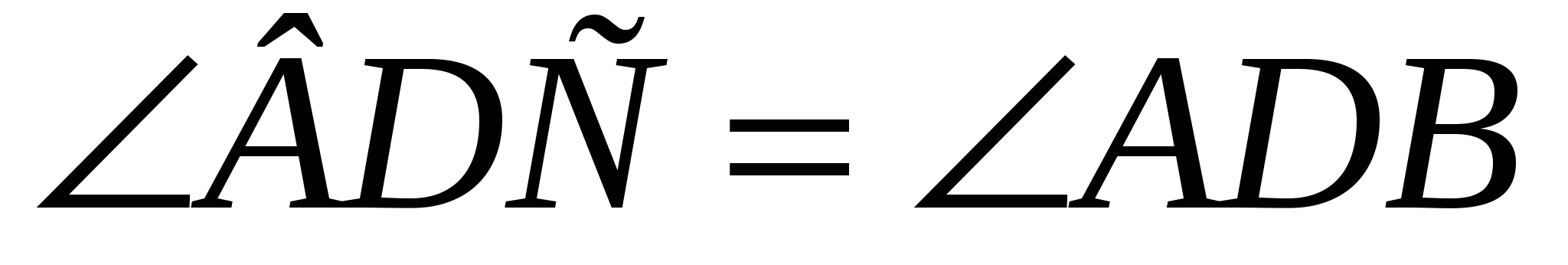 ) )
Доказательство:
AB = AD (по определению ромба),  ▲BAD равнобедренный. ▲BAD равнобедренный.
АО = ОС, ВО = DО (т.к. ромб – параллелограмм),  АО – медиана равнобедренного ▲BAD, АО – медиана равнобедренного ▲BAD, АО – высота и биссектриса ▲BAD. АО – высота и биссектриса ▲BAD.
Поэтому АС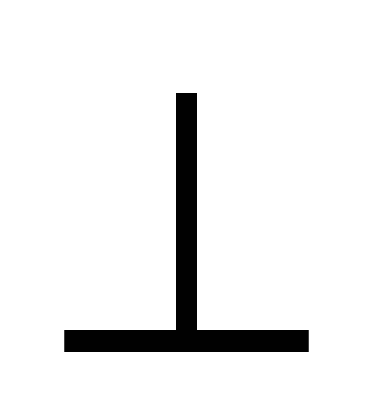 BD и BD и 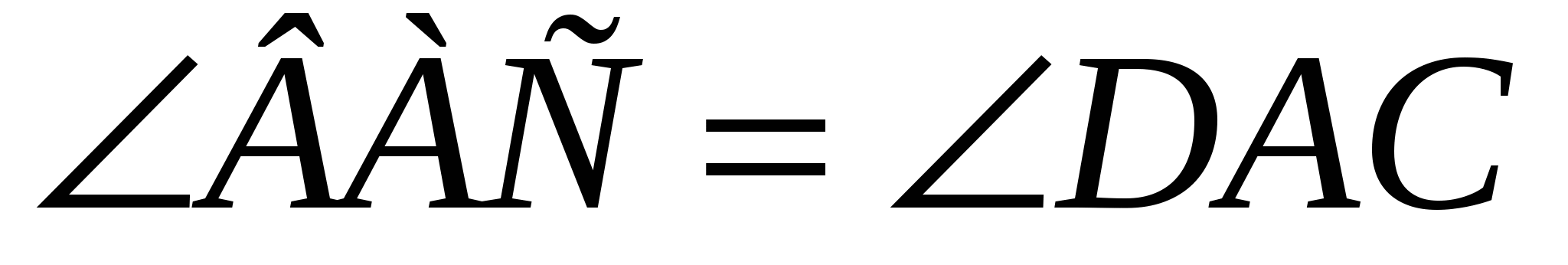 . .
(Равенство остальных углов ромба доказываются аналогично).
- Является ли прямоугольником четырёхугольник АВСD? В С Является ли прямоугольником четырёхугольник АВСD? В С
- Почему?
А D
- Такой четырёхугольник является ещё частным случаем прямоугольника, а значит и параллелограмма, и ромба - называется квадратом.
Определение. (Показ слайда)
Квадратом называется прямоугольник, у которого все стороны равны.
- Значит квадрат обладает всеми свойствами прямоугольника и ромба.
- Перечислите все свойства квадрата.
Все углы квадрата прямые.
Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
3. Физкультминутка. ( «Истинно-ложно»)
Я скажу несколько математических предложений. Если предложение верное, то вы сидите, если оно ложное, то вы встаёте, и кто-то из вас объясняет, почему ложное.
Параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны. (+)
В параллелограмме противоположные стороны и противоположные углы равны. (+)
В параллелограмме диагонали равны. (-)
В параллелограмме диагонали точкой пересечения делятся пополам. (+)
Диагонали прямоугольника точкой пересечения делятся пополам. (+)
Сумма углов выпуклого четырёхугольника равна 180◦. (-)
В прямоугольнике противоположные стороны равны. (+)
Ромб обладает всеми свойствами прямоугольника. (-)
Квадрат не обладает всеми свойствами ромба. (-)
Квадрат обладает всеми свойствами параллелограмма, прямоугольника, ромба. (+)
4. Применение знаний, формирование умений и навыков.
( Цель этапа – применение свойств ромба и квадрата при решении геометрических задач).
Задача.
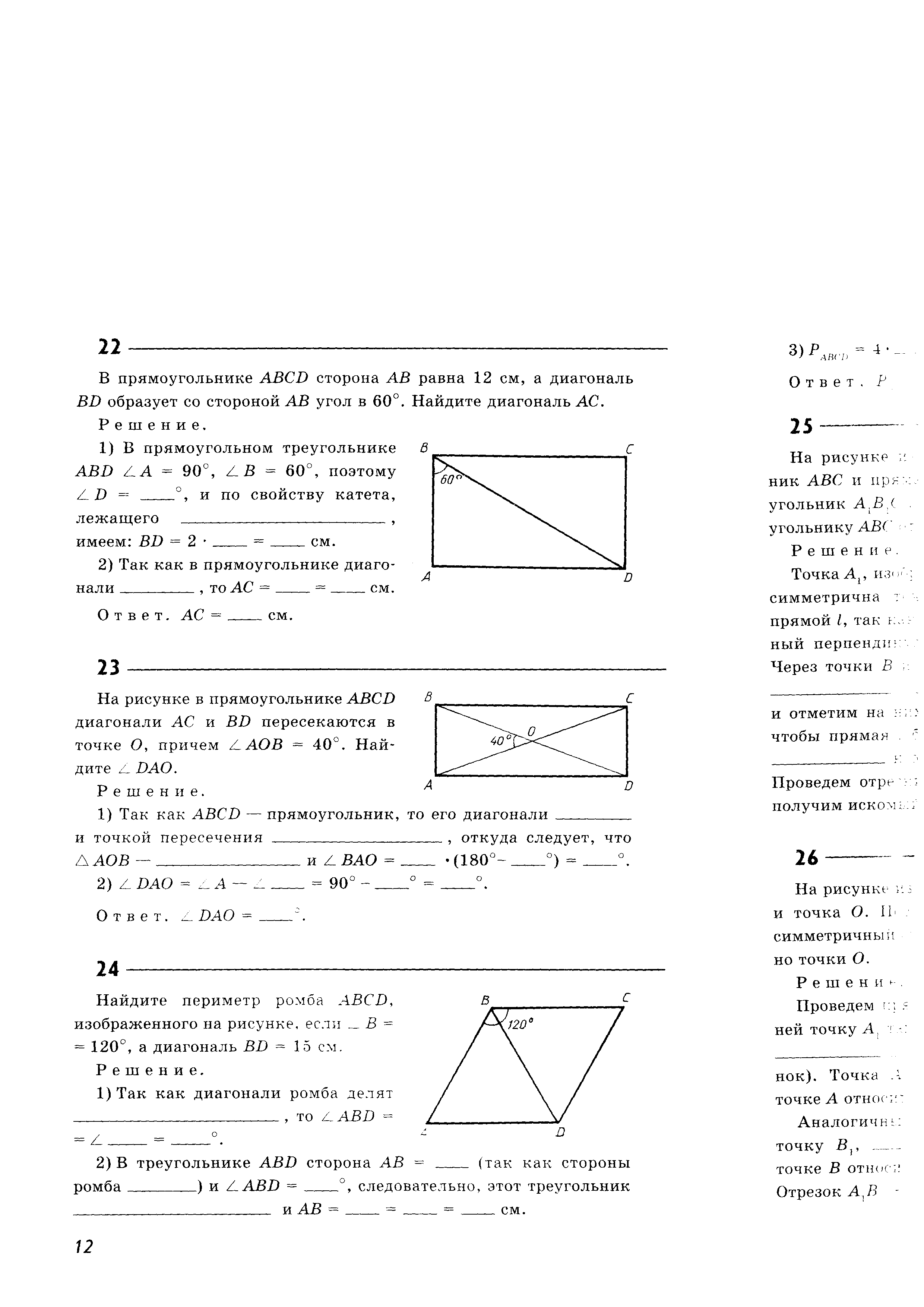 Найдите периметр ромба ABCD, изображённого на рисунке, если Найдите периметр ромба ABCD, изображённого на рисунке, если 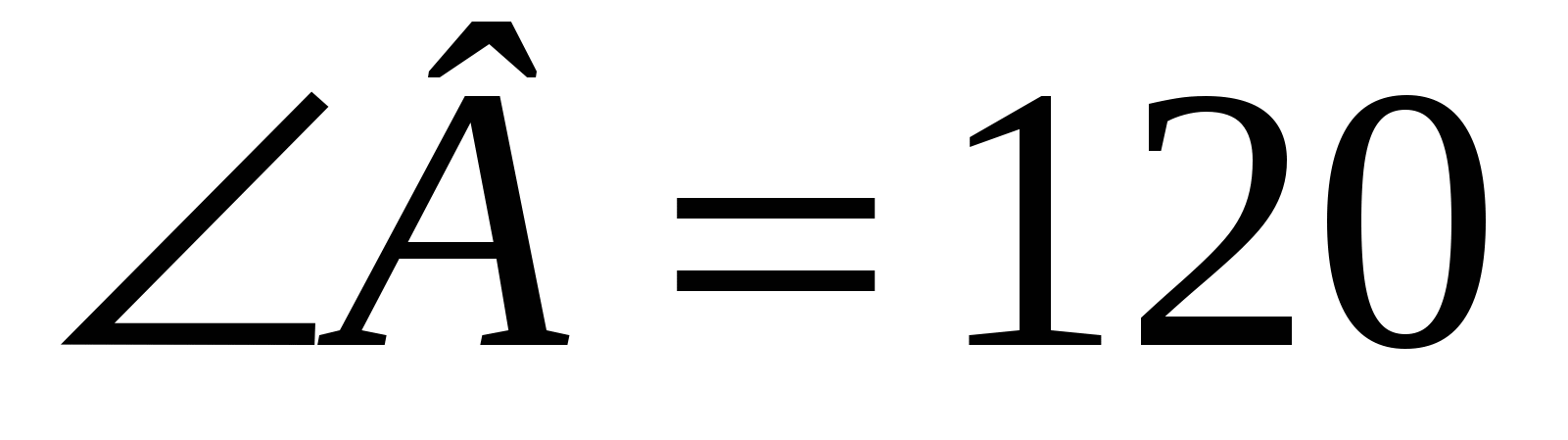 ◦, а диагональ BD = 15 см. ◦, а диагональ BD = 15 см.
Решение.
1)Так как диагонали ромба делят углы пополам,
то 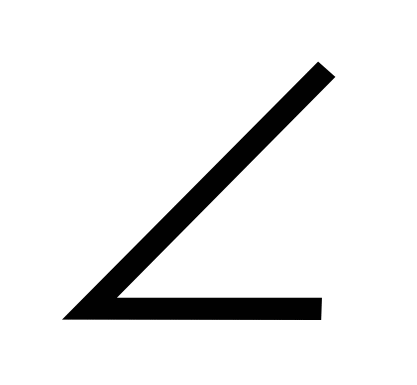 ABD = ABD = 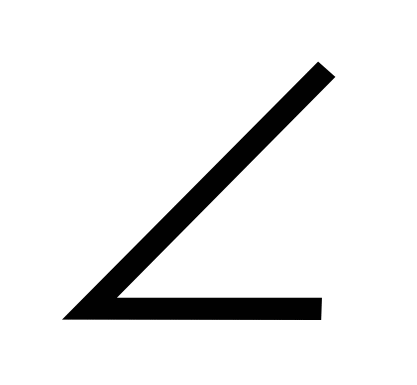 DBC = 60◦. DBC = 60◦.
2)В треугольнике ABD сторона АВ = AD (так как стороны ромба равны)
следовательно, этот треугольник равнобедренный с основанием ВD и
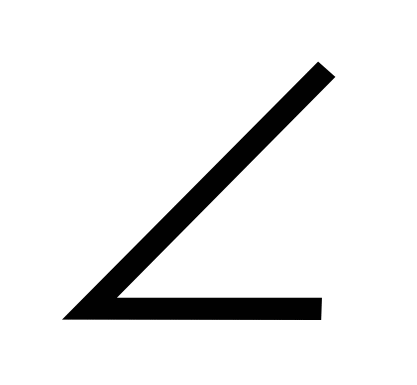 ABD = ABD =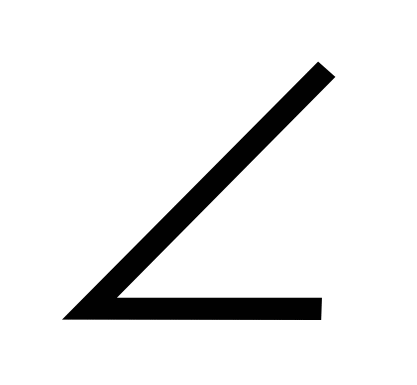 ADВ = 60◦. Так как сумма углов треугольника равна 180◦, то ADВ = 60◦. Так как сумма углов треугольника равна 180◦, то 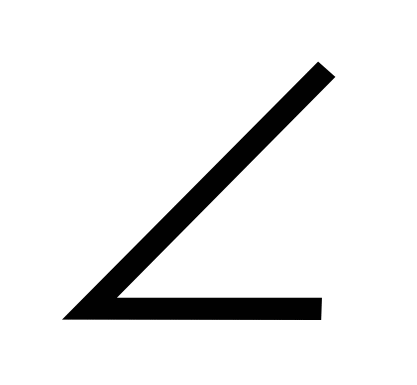 DАВ= 60◦, следовательно, треугольник ABD равносторонний, значит DАВ= 60◦, следовательно, треугольник ABD равносторонний, значит
АВ = BD = AD = 15 см
3)PABCD =4 * 15 см = 60 см. Ответ: PABCD = 60 см.
5. Теоретическая самостоятельная работа. (Самоанализ и самооценка)
- Заполните таблицу, отметив знаки + (да) и – (нет).
|
параллелограмм
|
прямоугольник
|
ромб
|
квадрат
|
1. Противолежащие стороны параллельны и равны
|
|
|
|
|
2. Все стороны равны
|
|
|
|
|
3. Противолежащие стороны равны, сумма соседних углов равна 180°
|
|
|
|
|
4. Все углы прямые
|
|
|
|
|
5. Диагонали пересекаются и точкой пересечения делятся пополам
|
|
|
|
|
6. Диагонали равны
|
|
|
|
|
7. Диагонали взаимно перпендикулярны и являются биссектрисами его углов
|
|
|
|
|
- Проверьте самостоятельно и поставьте себе оценку.
Критерий выставления оценки:
Оценка «5» - все ответы верные.
Оценка «4» - допущены ошибки.
Оценка «3» - допущены ошибки.
Оценка «2» - допущены ошибки.
|
параллелограмм
|
прямоугольник
|
ромб
|
квадрат
|
1. Противолежащие стороны параллельны и равны
|
+
|
+
|
+
|
+
|
2. Все стороны равны
|
-
|
-
|
+
|
+
|
3. Противолежащие стороны равны, сумма соседних углов равна 180°
|
+
|
+
|
+
|
+
|
4. Все углы прямые
|
-
|
+
|
-
|
+
|
5. Диагонали пересекаются и точкой пересечения делятся пополам
|
+
|
+
|
+
|
+
|
6. Диагонали равны
|
-
|
+
|
-
|
+
|
7. Диагонали взаимно перпендикулярны и являются биссектрисами его углов
|
-
|
-
|
+
|
+
|
Учащиеся подсчитывают «+», заработанные на уроке, и пользуясь алгоритмом, предложенным учителем, выставляют себе отметку за урок.
6. Подведение итогов.
- Что нового вы узнали сегодня на уроке?
- Дайте определение ромба? Квадрата?
- Назовите особое свойство ромба?
- Перечислите свойства квадрата?
7. Постановка домашнего задания.
Намечают пути дальнейшей работы со свойствами и признаками ромба, квадрата и других четырёхугольников, что позволяет мотивировать следующее домашнее задание:
1. пункт 46, стр. 109-110.
2. №406.
Анализ урока
I. Какова роль компьютера на уроке?
Компьютер помогает:
соединять слово, образ и действие (Я услышал и забыл. Я увидел и запомнил. Я сделал и понял);
обогатить знания учащихся по использованию ИКТ на других уроках и разных жизненных ситуациях;
позволяет экономить время на уроке по выполнению чертежей и записей;
визуально представить результаты работы в парах для дальнейшего обсуждения;
осуществлять проверку решений в режиме диалога, поскольку смену слайдов предваряют вопрос учителя и ответ учащихся;
помогает оперативно проверить правильность выполненного теста здесь и сейчас;
сохранить информацию для уроков повторения, а также для учащихся, пропустивших урок, предложив на диске презентацию домой;
самим учащимся быстро корректировать свои записи
(«черновик превращать в чистовик»);
систематизировать знания, полученные на уроках геометрии по данной теме;
повышает интерес к предмету.
II. Какие ставились задачи для повышения эффективности обучения?
На традиционном уроке изучения свойств и признаков какого-либо четырёхугольника, учитель чаще всего сам проводит доказательство свойств и признаков, причем то, которое дано в учебнике, а учащиеся записывают его в свои тетради. Записывают, не задумываясь, «ведь учитель знает, что пишет». Такое списывание приводит учащихся к безделью на уроке. Не секрет, что доказательство этих свойств и признаков быстро забываются учащимися. Поэтому мы должны стремиться не столько к запоминанию, сколько к логическому обоснованию суждений, выработке у учащихся умений и навыков, благодаря которым они в состоянии самостоятельно разобраться в них. Для этого полезны учебные задания на поиск идеи, шагов доказательства и их обоснования, что и сделано на уроке.
Другой путь активизации деятельности учащихся связан с отысканием способа доказательства свойств и признаков ромба и квадрата. Поэтому на уроке предложена работа по учебнику Л.С. Атанасяна, вариант учителя, и самостоятельный поиск доказательства основного свойства ромба. Сравнение вариантов доказательств даст возможность еще раз поговорить о логическом строении геометрии.
Теоретическая самостоятельная работа позволила систематизировать имеющиеся знания учащихся по свойствам четырёхугольников. Это является немало важным при повторении курса геометрии в 8 классе.
Работа в парах организована таким образом, что позволяет каждому:
приобрести новый коммуникативный опыт;
обогатить видение предложенной проблемы;
совершенствовать технику дискуссий (умение формулировать высказывания, аргументировать свою точку зрения, соотносить свою точку зрения с другими, критически подходить к своему мнению и мнению окружающих, а в итоге корректировать свою позицию);
проявить инициативу, самостоятельность, избирательность в способах работы;
почувствовать уважение к себе и проявить терпимость к другим.
  |
|
|
 Скачать 120.69 Kb.
Скачать 120.69 Kb.


 Учитель математики: Руденко О.Н.
Учитель математики: Руденко О.Н.













 ОУ «Немёрзская ООШ»
ОУ «Немёрзская ООШ» айдите периметр прямоугольника ABCD, изображённого на рисунке, если биссектриса угла В пересекает сторону AD в точке Е и делит её на отрезки АЕ = 17 см и ЕD = 21 см.
айдите периметр прямоугольника ABCD, изображённого на рисунке, если биссектриса угла В пересекает сторону AD в точке Е и делит её на отрезки АЕ = 17 см и ЕD = 21 см. прямоугольнике ABCD сторона АВ = 12 см, а диагональ BD образует со стороной АВ угол в 60◦. Найдите диагональ АС.
прямоугольнике ABCD сторона АВ = 12 см, а диагональ BD образует со стороной АВ угол в 60◦. Найдите диагональ АС. ◦. Найдите
◦. Найдите 
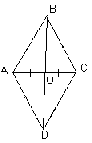
 Является ли прямоугольником четырёхугольник АВСD? В С
Является ли прямоугольником четырёхугольник АВСD? В С Найдите периметр ромба ABCD, изображённого на рисунке, если
Найдите периметр ромба ABCD, изображённого на рисунке, если