Конспект урока по алгебре и началам анализа в 11 классе учителя математики Платоновой Н. С. по теме: «Решение логарифмических уравнений»
 Скачать 63.28 Kb.
|
| Конспект урока по алгебре и началам анализа в 11 классе учителя математики Платоновой Н. С. по теме: «Решение логарифмических уравнений». Цели урока: Обучающие: закрепить основные понятия по заданной теме: определение и свойства логарифмов и логарифмической функции, правила вычисления логарифмов, способы решения логарифмических уравнений. Развивающие: содействовать развитию логического мышления учащихся, Развивать умение рассуждать, сравнивать, осмысливать материал; развивать навыки исследовательской деятельности; развивать навыки общения. Воспитывающие: воспитание познавательного интереса, элементов культуры общения; побуждение учащихся к преодолению трудностей в процессе умственной деятельности; воспитании у учащихся уверенности в себе, веры в свои силы в нестандартной ситуации. Ход урока.
задачи урока). Изучив основные свойства логарифмической функции, правила вычисления логарифмов и свойств логарифмов, наша основная задача на сегодняшний урок – научиться решать логарифмические уравнения.
Устная работа. На столах учащихся и на интерактивной доске находится шпаргалка, которая отображает весь изученный материал. По этому материалу вспоминаем изученное. Тренировочный тест. На каком из рисунков изображён график функции 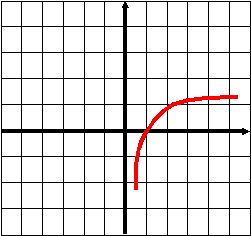 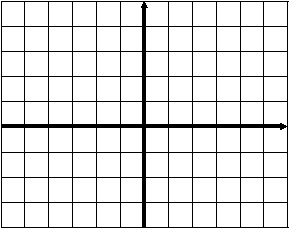?   На каком из рисунков изображён график функции 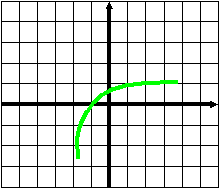 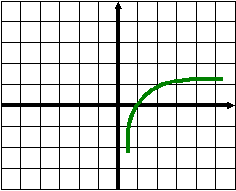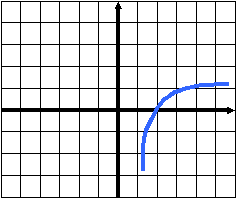?   Найдите область определения функции  .X<5 0 Найдите область определения функции  X<- 0.25 0 Определите характер монотонности функции  Определите характер монотонности функции  Вычислите :         8 25 Сравните числа  
Открыли тетради и записали тему урока: Логарифмические уравнения. Уравнения вида  где a > 0, a  1, называют логарифмическими уравнениями, если  , то решение  Переход от одного уравнения к другому называют потенцированием (т. е. освобождение от знака логарифма за счёт монотонности логарифмической функции, т. к. монотонная функция принимает каждое своё значение один раз). Теперь мы должны с вами научиться решать логарифмические уравнения. На предыдущих уроках мы с вами рассмотрели один из методов решения простейших логарифмических уравнений – функционально-графический. Он заключается в построении графиков функций в одной системе координат и нахождении точки пересечения этих графиков, являющейся решением данного уравнения. Методы решения:
 Решение. ОДЗ:   Потенцируя получим:   По формулам Виета найдём корни: 4 и -3. Выполнив проверку, убедимся, что 4 не является корнем. Запишем ответ. Ответ:-3.
 Решение. ОДЗ: х+4>0, 2x+3>0, x  (-1,5;0,5).1- 2x>0. Вспомним свойства логарифмов – сумма логарифмов двух положительных чисел равна логарифму произведения этих чисел. Получим:  Освобождаясь от знака логарифма и решив квадратное уравнение получим корни: -5,5 и -1. Согласовав корни с ОДЗ. получим корень: -1. Ответ: - 1.
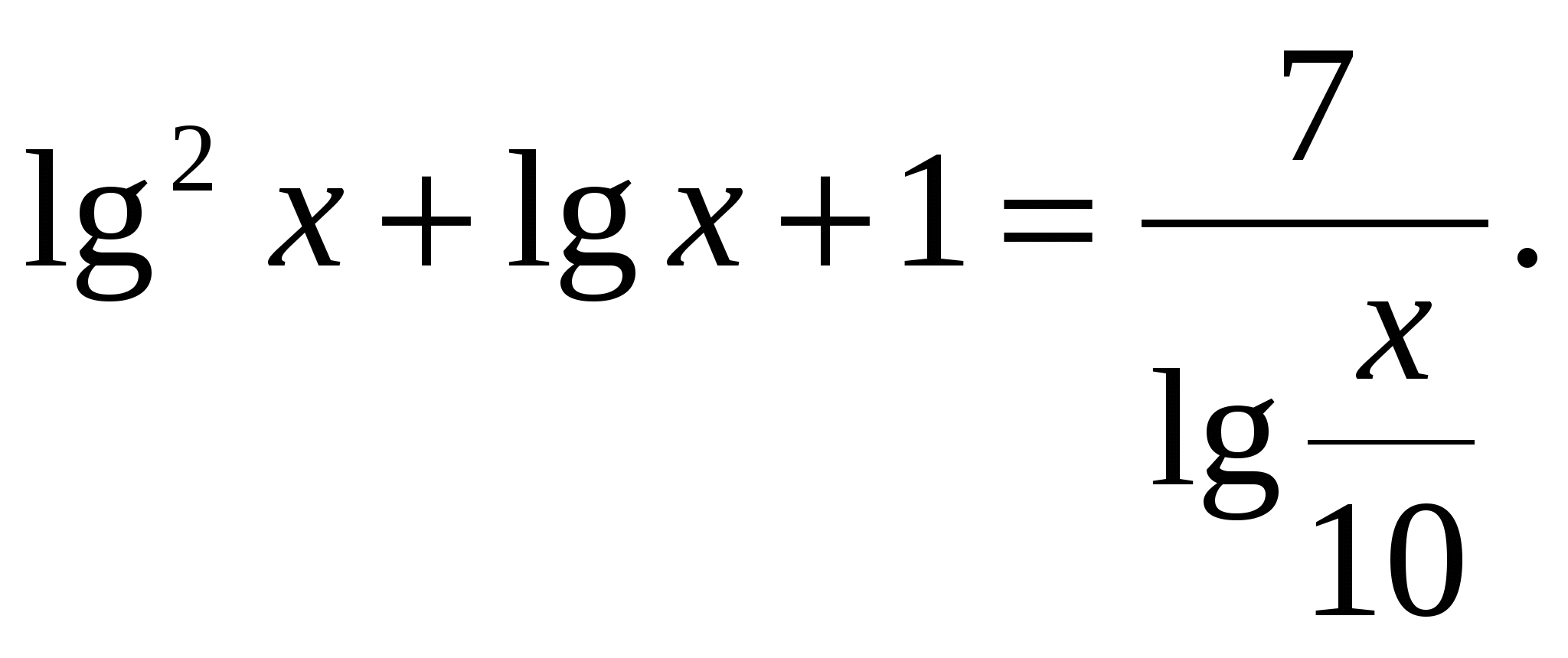 Решение. ОДЗ: х>0, x 10.Преобразуем   ,Введём замену  тогда  ОДЗ:      .Вернёмся к замене:    Ответ: 100.
Мордкович стр. 230 №№ 1549(а),  1550(а),  1552(а),  1553(а),  1554(а),  1558(а),  1559(а). 
А сейчас мы выполним обучающую самостоятельную работу (на листочках). Вариант 1. Решите уравнения: 1.  1) найдите ОДЗ., 2) освободитесь от знака логарифма, 3) решите получившееся уравнение, 4) согласуйте найденные корни с ОДЗ, 5) запишите ответ. 2.  3.  1) найдите ОДЗ, 2) введите замену, 3) решите полученное уравнение, 4) выполните обратную замену, 5) согласуйте корни с ОДЗ, 6) запишите ответ. 4.  1) запишите ОДЗ, 2) вспомните определение логарифма, 3) решите полученное уравнение, 4) согласуйте корни с ОДЗ, 5) запишите ответ. Вариант 2. Решите уравнения: 1.  1) найдите ОДЗ., 2) освободитесь от знака логарифма, 3) решите получившееся уравнение, 4) согласуйте найденные корни с ОДЗ, 5) запишите ответ. 2.  3.  1) найдите ОДЗ, 2) введите замену, 3) решите полученное уравнение, 4) выполните обратную замену, 5) согласуйте корни с ОДЗ, 6) запишите ответ. 4.  1) запишите ОДЗ, 2) вспомните определение логарифма, 3) решите полученное уравнение, 4) согласуйте корни с ОДЗ, 5) запишите ответ. Взаимопроверка (обменялись тетрадями). 1 Вариант. 1. 1) 4х+5 > 0, 9-2х > 0. ( -1,25; 4,5) 2) 4x+5=9-2x, 3) 4x+2x=9-5. 6x=4. x=  .4)  5) Ответ: 
2)    3)  4) Ответ: 7.
2)  3)    4)       5)  6) Ответ:  4. 1)  2)  3)   4)  ОДЗ,  ОДЗ,5) Ответ: -4, 3. 2 Вариант. 1. 1) 3х-4>0, 12-5x>0, (  ;2,4),2) 3x-4=12-5x, 3) 3x+5x=12+4, 8x=16, x=2,
  3)  4) Ответ: 10.
2)  3)    4)        5)  6) Ответ:  4. 1)  2)  3)   4)  ОДЗ,  ОДЗ,5) Ответ: -5, 2. Работа оценивается следующим образом: 4 задания – «5», 3 задания – «4», 2 задания – «3», 1 задание – «2». Оценили работы и сдали листочки.
1559(г). |
