| Купить люстру италия в интернет магазине Большой выбор свет. оборудования - купить люстру италия в интернет магазине. Lightil. lightil.ru | Бра классика на стене Большой выбор свет. оборудования - бра классика на стене. Lightil. lightil.ru |
Рабочая программа учебной дисциплины одп. 01 Математика 100107. 01 «Слесарь по эксплуатации и ремонту газового оборудования»
 Скачать 450.18 Kb. Скачать 450.18 Kb.
|
1 2
| Главное Управление образования Курганской области ГБОУ СПО «Шадринский политехнический колледж» Начальное профессиональное образование РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ ОДП.01 МАТЕМАТИКА 100107.01 «Слесарь по эксплуатации и ремонту газового оборудования» 2012 год  ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Примерная программа учебной дисциплины «Математика» предназначена для изучения математики в учреждениях начального профессионального образования, реализующих образовательную программу среднего (полного) общего образования, при подготовке квалифицированных рабочих по профессии 100107.01 «Слесарь по эксплуатации и ремонту газового оборудования». Согласно «Рекомендациям по реализации образовательной программы среднего (полного) общего образования в образовательных учреждениях начального профессионального и среднего профессионального образования в соответствии с федеральным базисным учебным планом и примерными учебными планами для образовательных учреждений Российской Федерации, реализующих программы общего образования» (письмо Департамента государственной политики и нормативно-правового регулирования в сфере образования Минобрнауки России от 29.05.2007 № 03-1180) математика в учреждениях начального профессионального образования изучается с учетом профиля получаемого профессионального образования. Математика изучается как профильный учебный предмет при освоении профессий НПО социально – экономического профиля в объеме 342 часа. Примерная программа ориентирована на достижение следующих целей:
к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей. Основу примерной программы составляет содержание, согласованное с требованиями федерального компонента государственного стандарта среднего (полного) общего образования базового уровня. В программе учебный материал представлен в форме чередующегося развертывания основных содержательных линий:
Развитие содержательных линий сопровождается совершенствованием интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления. Математика является фундаментальной общеобразовательной дисциплиной со сложившимся устойчивым содержанием и общими требованиями к подготовке обучающихся. Реализация общих целей изучения математики традиционно формируется в четырех направлениях – методическое (общее представление об идеях и методах математики), интеллектуальное развитие, утилитарно-прагматическое направление (овладение необходимыми конкретными знаниями и умениями) и воспитательное воздействие. Профилизация целей математического образования отражается на выборе приоритетов в организации учебной деятельности обучающихся. Для технического профиля выбор целей смещается в прагматическом направлении, предусматривающем усиление и расширение прикладного характера изучения математики; преимущественной ориентации на алгоритмический стиль познавательной деятельности. Изучение математики как профильного учебного предмета обеспечивается: – выбором различных подходов к введению основных понятий; – формированием системы учебных заданий, обеспечивающих эффективное осуществление выбранных целевых установок; – обогащением спектра стилей учебной деятельности за счет согласования с ведущими деятельностными характеристиками выбранной профессии. Профильная составляющая отражается в требованиях к подготовке обучающихся в части: – общей системы знаний: содержательные примеры использования математических идей и методов в профессиональной деятельности; – умений: различие в уровне требований к сложности применяемых алгоритмов; – практического использования приобретенных знаний и умений: индивидуального учебного опыта в построении математических моделей, выполнении исследовательских и проектных работ. Для профессии 100107.01 «Слесарь по эксплуатации и ремонту газового оборудования» профессионально значимыми являются, в первую очередь, знания и навыки расчетного характера, умение выполнять действия с числами разного знака, оперировать обыкновенными и десятичными дробями, умение оперировать процентами. В техническом обиходе активно используются такие математические понятия, как соотношение величин, пропорции, степень числа, решаются уравнения. Реализация профильного компонента программы достигается: -выделением большего числа часов на изучение профессионально значимых для сварщиков тем; - учетом в программе перечня учебных элементов курсов спец.дисциплин по обучению профессии 100107.01 «Слесарь по эксплуатации и ремонту газового оборудования»; - выделением в конце тем специальных учебных умений, ориентированных на конкретные темы курсов спец.дисциплин; - решением задач с производственным содержанием; - нахождение кратчайших и безопасных путей при прокладке газопровода; - выделением вопросов экономии газа, рационального использования расходных материалов. Таким образом, программа подчеркивает значимость математических знаний для подготовки обучающихся по профессии 100107.01 «Слесарь по эксплуатации и ремонту газового оборудования» . Содержание учебной дисциплины Введение Математика в науке, технике, экономике, информационных технологиях и практической деятельности. Цели и задачи изучения математики в учреждениях начального и среднего профессионального образования. АЛГЕБРА Развитие понятия о числе Целые и рациональные числа. Действительные числа. Приближенные вычисления. Вычисление процентов. Требования к знаниям обучающихся: Должны знать:
Должны уметь:
Практические занятия: 1.Решение задач, связанных с законами арифметических действий и их применение к упрощению выражений. 2.Решение задач на пропорции. 3.Решение задач на проценты. 4.Решение примеров на вычисление модуля и вычисление приближенных значений. 5.Решение задач с производственным содержанием. Степени, корни и логарифмы Корни и степени. Корни натуральной степени из числа и их свойства. Степени с рациональными показателями, их свойства. Степени с действительными показателями. Логарифм. Логарифм числа. Основное логарифмическое тождество. Десятичные и натуральные логарифмы. Правила действий с логарифмами. Преобразование алгебраических выражений. Преобразование рациональных, иррациональных, степенных, показательных и логарифмических выражений. Требования к знаниям обучающихся: Должны знать:
Должны уметь:
Практические занятия: 1.Вычисление корней. Применение свойств корней. 2.Преобразование иррациональных выражений. 3.Действия над степенями. 4.Преобразование степенных выражений. 5.Преобразование алгебраических выражений, содержащих степени и корни. 6.Вычисление логарифмов. 7-8.Преобразование логарифмических выражений. 9. Преобразование иррациональных, степенных и логарифмических выражений. Тригонометрические функции Виды тригонометрических функций. Свойства функции: область определения, область значений, четность, нечетность, периодичность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, промежутки знакопостоянства. Построение графиков тригонометрических функций, растяжение и сжатие их вдоль осей координат. Требования к знаниям обучающихся: Должны знать:
Должны уметь:
Практические занятия: 1.Построение графика и исследование функции у = tgx. 2. Построение графика и исследование функции у = сtgx. 3-4. Построение графиков тригонометрических функций. Основы тригонометрии Радианная мера угла. Вращательное движение. Синус, косинус, тангенс и котангенс числа. Основные тригонометрические тождества, формулы приведения. Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Преобразования суммы тригонометрических функций в произведение и произведения в сумму. Преобразования простейших тригонометрических выражений. Простейшие тригонометрические уравнения. Решение тригонометрических уравнений. Простейшие тригонометрические и неравенства. Арксинус, арккосинус, арктангенс числа. Требования к знаниям обучающихся: Должны знать:
Должны уметь:
Практические занятия: 1.Решение примеров на перевод радиан в градусы, а градусы в радианы. 2.Применение формул приведения к преобразованию тригонометрических выражений. 3. Применение формул сложения к преобразованию тригонометрических выражений. 4. Применение формул суммы и разности синуса и косинуса к преобразованию тригонометрических выражений. 5.Нахождение значений обратных тригонометрических функций. 6-7.Решение простейших тригонометрических уравнений. 8-9.Решение тригонометрических уравнений, приводимых к неполным квадратным уравнениям. 10. Решение тригонометрических уравнений, приводимых к квадратным уравнениям. 11-12. Решение тригонометрических уравнений. 13-14. Решение тригонометрических неравенств. 15-16. Решение тригонометрических уравнений и неравенств. Функции, их свойства и графики Функции. Область определения и множество значений; график функции, построение графиков функций, заданных различными способами. Свойства функции: монотонность, четность, нечетность, ограниченность, периодичность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума. Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях. Обратные функции. Область определения и область значений обратной функции. График обратной функции. Арифметические операции над функциями. Сложная функция (композиция). Требования к знаниям обучающихся: Должны знать:
Должны уметь:
Практические занятия: 1.Построение графиков линейной и квадратичной функций. 2. Построение графиков обратной функции. 3. Примеры функциональных зависимостей в реальных процессах и явлениях. 4. Исследование функции по графику. Степенные, показательные, логарифмические функции Определения функций, их свойства и графики. Преобразования графиков. Параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой y = x. Требования к знаниям обучающихся: Должны знать:
Должны уметь:
Практические занятия: 1. Построение графика степенной функций. 2. Преобразование графиков степенной функции. 3. Построение графика показательной функций. 4. Преобразование графиков показательной функции. 5.Нахождение области определения логарифмической функции. 6. Построение графика логарифмической функций. 7. Преобразование графиков логарифмической функции. 8. Определение свойств функции по графику. 9. Преобразование графиков степенной, показательной и логарифмической функций. НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА Последовательности. Способы задания и свойства числовых последовательностей. Понятие о пределе последовательности. Суммирование последовательностей. Производная. Понятие о производной функции, её геометрический и физический смысл. Уравнение касательной к графику функции. Производные суммы, разности, произведения, частного. Производные основных элементарных функций. Применение производной к исследованию функций и построению графиков. Примеры использования производной для нахождения наилучшего решения в прикладных задачах. Вторая производная, ее геометрический и физический смысл. Применение производной к исследованию функций и построению графиков. Нахождение скорости для процесса, заданного формулой и графиком. Первообразная и интеграл. Применение определенного интеграла для нахождения площади криволинейной трапеции. Формула Ньютона—Лейбница. Примеры применения интеграла в физике и геометрии. Требования к знаниям обучающихся: Должны знать:
Должны уметь:
Практические занятия: 1-2.Решение примеров на нахождение производной по правилам дифференцирования. 3-4.Решение примеров на нахождение производной показательной и логарифмической функций. 5-6. Решение примеров на нахождение производной тригонометрических функций. 7-10. Исследование функции с помощью производной. 11-12.Нахождение наибольших и наименьших значений функции с помощью производной. 13.Нахождение углового коэффициента касательной. 14-15.Уравнение касательной к графику функции. 16.Решение задач по теме: «Производная в физике и технике». 17.Решение примеров на нахождение первообразной. 18-19. Решение примеров на нахождение интеграла. 20-22.Вычисление криволинейной трапеции. 23. Решение примеров по теме: «Первообразная и интеграл». Уравнения и неравенства Равносильность уравнений, неравенств, систем. Рациональные, иррациональные, показательные уравнения и системы. Основные приемы их решения (разложение на множители, введение новых неизвестных, подстановка, графический метод). Рациональные, иррациональные, показательные неравенства. Основные приемы их решения. Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем. Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений. Требования к знаниям обучающихся: Должны знать:
Должны уметь:
Практические занятия: 1.Решение линейных уравнений. 2.Решение линейных неравенств. 3.Решение систем линейных уравнений. 4.Решение систем линейных неравенств. 5.Решение квадратных уравнений. 6-7. Решение квадратных неравенств. 8.Решение систем нелинейных неравенств. 9-10.Решение иррациональных уравнений. 11-12.Решение простейших показательных уравнений. 13-14. Решение показательных уравнений. 15. Решение простейших показательных неравенств. 16. Решение показательных неравенств. 17.Решение систем уравнений, содержащих показательные уравнения. 18. Решение простейших логарифмических уравнений. 19-20. Решение логарифмических уравнений. 21-22. Решение логарифмических неравенств. 23-24. Решение систем логарифмических уравнений. 25.Решение примеров по теме: «Уравнения и неравенства». КОМБИНАТОРИКА, СТАТИСТИКА И ТЕОРИЯ ВЕРОЯТНОСТЕЙ Элементы комбинаторики Основные понятия комбинаторики. Задачи на подсчет числа размещений, перестановок, сочетаний. Решение задач на перебор вариантов. Формула бинома Ньютона. Свойства биноминальных коэффициентов. Треугольник Паскаля. Требования к знаниям обучающихся: Должны знать:
Должны уметь:
Практические занятия: 1.Решение задач на подсчет перестановок. 2. Решение задач на подсчет размещений. 3. Решение задач на подсчет сочетаний. 4-5. Решение задач на подсчет комбинаторных задач с повторениями. 6. Решение задач на перебор вариантов. 7. Решение задач с практическим применением. 8. Решение задач с применением бинома Ньютона. 9. Решение задач с применением треугольника Паскаля. Элементы теории вероятностей. Элементы математической статистики Событие, вероятность события, сложение и умножение вероятностей. Представление данных (таблицы, диаграммы, графики), Решение практических задач с применением вероятностных методов. Требования к знаниям обучающихся: Должны знать:
Должны уметь:
Практические занятия: 1-2Решение практических задач, с применением вероятностных методов. 3.Решение вероятностных задач. 4-5. Решение статистических задач. ГЕОМЕТРИЯ Прямые и плоскости в пространстве Взаимное расположение двух прямых в пространстве. Параллельность прямой и плоскости. Параллельность плоскостей. Перпендикулярность прямой и плоскости. Перпендикуляр и наклонная. Угол между прямой и плоскостью. Двугранный угол. Угол между плоскостями. Перпендикулярность двух плоскостей. Геометрические преобразования пространства: параллельный перенос, симметрия относительно плоскости. Параллельное проектирование. Изображение пространственных фигур. Требования к знаниям обучающихся: Должны знать:
Должны уметь:
Практические занятия: 1.Решение задач на параллельность прямых в пространстве. 2-3.Решение задач на параллельность прямых и плоскостей в пространстве. 4-5. Решение задач на параллельность плоскостей. 6. Решение задач на перпендикулярность прямых в пространстве. 7-8. Решение задач на перпендикулярность прямых и плоскостей в пространстве. 9-10. Решение задач на перпендикулярность прямых и плоскостей в пространстве. 11-12. Решение задач на перпендикулярность плоскостей в пространстве. 13-14. Решение задач на нахождение угла между плоскостями. 15. Решение задач на геометрические преобразования в пространстве. 16. Решение задач по теме: «Прямые и плоскости в пространстве». Многогранники Вершины, ребра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники. Призма. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб. Пирамида. Правильная пирамида. Усеченная пирамида. Тетраэдр. Симметрии в кубе, в параллелепипеде. Сечения куба, призмы и пирамиды. Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр). Требования к знаниям обучающихся: Должны знать:
Должны уметь:
Практические занятия: 1-2.Изображение призмы и построение ее сечений. 3.Решение задач на вычисление площади поверхности призмы. 4.Решение задач на вычисление площади поверхности параллелепипеда и куба. 5.Построение сечений куба плоскостью. 6. Изображение пирамиды и построение ее сечений. 7. Решение задач на вычисление площади поверхности пирамиды. 8. Решение задач на вычисление площади поверхностей многогранников. Тела и поверхности вращения Цилиндр и конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения, параллельные основанию. Шар и сфера, их сечения. Касательная плоскость к сфере. Требования к знаниям обучающихся: Должны знать:
Должны уметь:
Практические занятия: 1-2. Решение задач на нахождение основных элементов цилиндра и площади его сечений. 3.Решение задач на нахождение основных элементов конуса и площади его сечений. 4.Решение задач на нахождение основных элементов усеченного конуса и площади его сечений. 5.Решение задач с производственным содержанием. 6. Решение задач на нахождение основных элементов тел вращения. Измерения в геометрии Объем и его измерение. Интегральная формула объема. Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса. Формулы объема шара и площади сферы. Подобие тел. Отношения площадей поверхностей и объемов подобных тел. Требования к знаниям обучающихся: Должны знать:
Должны уметь:
Практические занятия: 1-2.Решение задач на нахождение объема куба и прямоугольного параллелепипеда. 3-4. Решение задач на нахождение объема призмы. 5-6. Решение задач на нахождение объема цилиндра. 7. Решение задач на нахождение объема пирамиды. 8. Решение задач на нахождение объема конуса. 9-10. Решение задач на нахождение площади поверхности цилиндра. 11-12. Решение задач на нахождение площади поверхности конуса. 13-15. Решение задач на нахождение объема шара и площади поверхности сферы. 16. Решение задач на нахождение объемов тел вращения. 17-18.Решение задач на отношение площадей поверхности и объемов подобных тел. 19-20. Решение задач по теме: «Объемы многогранников и тел вращения» Координаты и векторы Прямоугольная (декартова) система координат в пространстве. Формула расстояния между двумя точками. Уравнения сферы, плоскости и прямой. Векторы. Модуль вектора. Равенство векторов. Сложение векторов. Умножение вектора на число. Разложение вектора по направлениям. Угол между двумя векторами. Проекция вектора на ось. Координаты вектора. Скалярное произведение векторов. Использование координат и векторов при решении математических и прикладных задач. Требования к знаниям обучающихся: Должны знать:
Должны уметь:
Практические занятия: 1.Вычисление расстояния между двумя точками. 2.Составление уравнений сферы, плоскости, прямой. 3.Построение векторов в пространстве. Вычисление модуля вектора. 4.Разложение вектора по направлениям. 5.Нахождение скалярного произведения векторов и угла между векторами. 6.Использование координат и векторов при решении математических и прикладных задач. |
1 2
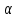 , как ординаты и абсциссы точки Р0 единичной окружности, соответственно, понятие функций синуса, косинуса, тангенса и котангенса;
, как ординаты и абсциссы точки Р0 единичной окружности, соответственно, понятие функций синуса, косинуса, тангенса и котангенса;