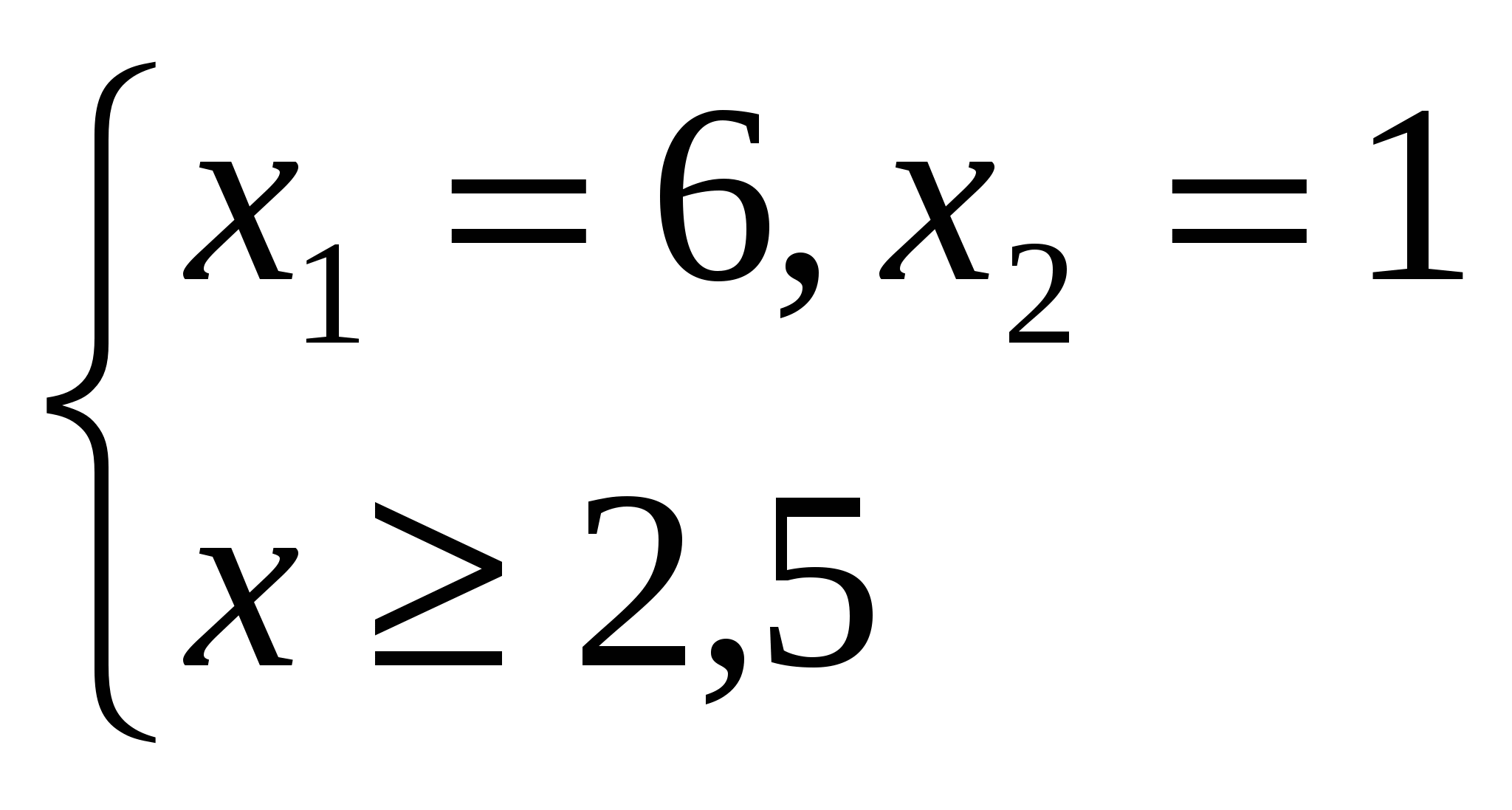|
Ход урока (занятия) Организационный момент
Ход урока (занятия)
Организационный момент:
Мотивация учащихся:
Деятельность учителя
|
Деятельность ученика
|
Ребята! Мы решали квадратные уравнения различными способами, выясняли связь между коэффициентами квадратного уравнения и количеством его корней.
Где же может быть использован полученный опыт работы с этими уравнениями?
Нет ли таких уравнений, при решении которых окажутся полезными навыки решения квадратных уравнений?
|
|
Сообщение темы занятия и целей занятия: факультативное занятие по теме «Уравнения, приводимые к квадратным». Эпиграфом к занятию является высказывание английского поэта А. Попа (1688-1744гг.): «Силу уму придают упражнения, а не покой».
Сообщение задач занятия: учащиеся должны научиться применять знания, полученные при решении квадратных уравнений, для решения уравнений нового типа «иррациональных».
Актуализация опорных знаний:
Деятельность учителя
|
Деятельность ученика
|
Ребята, дома вы приготовили контрольные вопросы, с помощью которых мы с вами повторим теоретический материал по теме «Квадратное уравнение и его корни» (каждая группа задает вопросы из своего списка, а другая группа на них отвечает).
|
Примерные вопросы, составленные учениками дома:
Как называется уравнение второй степени с одной переменной?
Сколько корней имеет квадратное уравнение, если D 0? 0?
Произведение корней квадратного уравнения равно…..
Равенство, содержащее переменную, значение которой нужно найти называют……
От чего зависит количество корней квадратного уравнения?
Чему равна сумма корней приведенного квадратного уравнения?
Как называют квадратное уравнение, у которого первый коэффициент 1?
Сколько корней имеет квадратное уравнение, если D  0? 0?
Что значит решить уравнение?
Как читается теорема Виета?
Уравнения, имеющие одни и те же корни, называются……
Какие виды квадратных уравнений существуют?
|
Таблицы 3 и 4 вывешиваются при перекрестном опросе учащихся.
Деятельность учителя
|
Деятельность ученика
|
Ребята, я попрошу вас обратить внимание на формулу в таблице 4, которую особенно удобно использовать при решении приведенного квадратного уравнения, когда p – четное число.
Для запоминания этой формулы можно использовать стихотворение (рассказывают два ученика):
p со знаком взяв обратным,
Мы на два его разделим.
И от корня аккуратно
Знаком «минус», «плюс» отделим.
А под корнем, очень кстати,
Половина p в квадрате,
Минус q –
И вот решенье
Небольшого уравненья.
Чтобы решить уравнение,
Корни его отыскать,
Нужно немного терпения,
Ручку, перо и тетрадь.
Минус напишем сначала,
Рядом с ним p пополам,
Плюс – минус знак радикала,
Ну, а под корнем, приятель,
Сводится все к пустяку,
P пополам и в квадрате
Минус несчастное q.
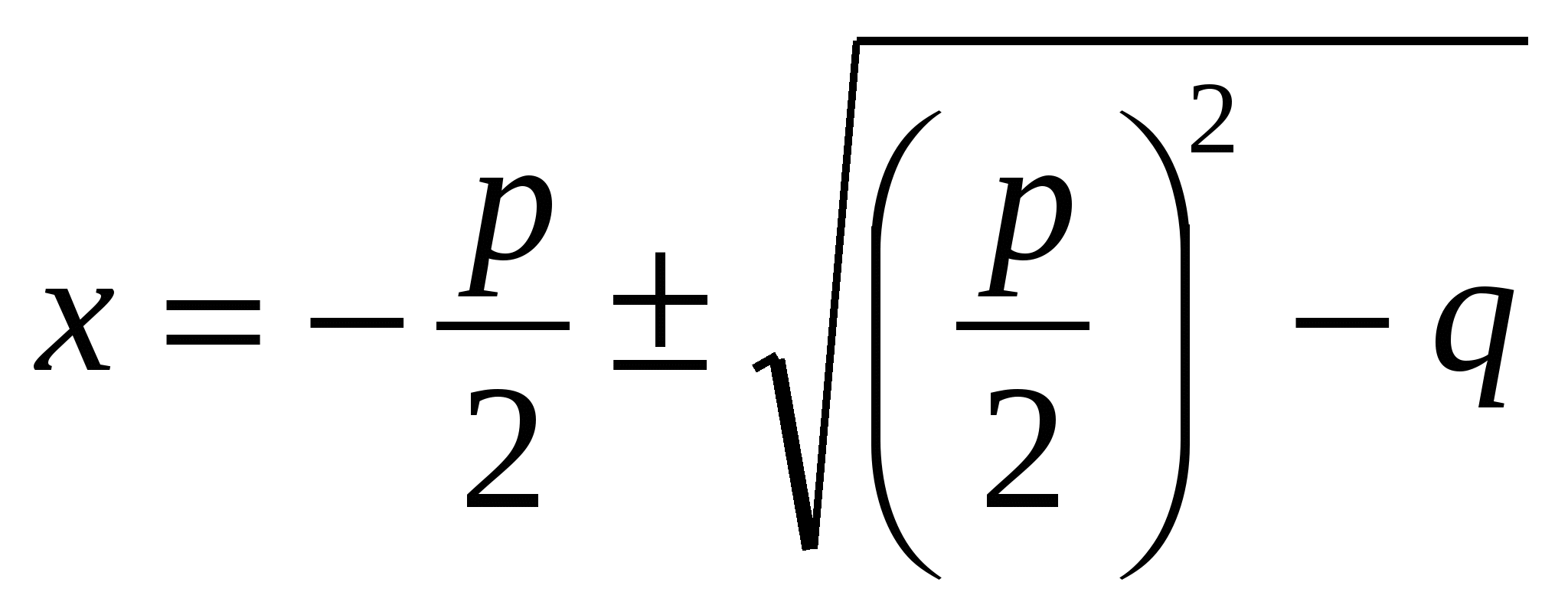
Решите уравнение 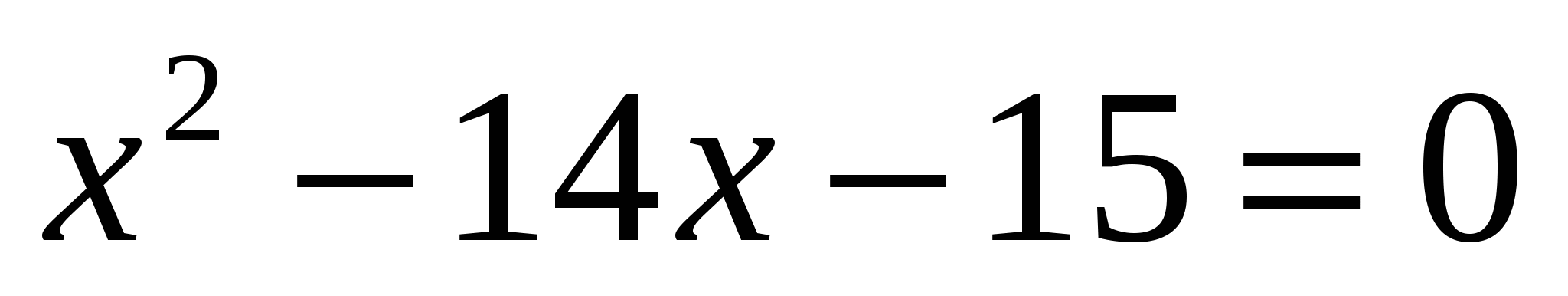 с помощью данной формулы. (Ответ: -1; 15) с помощью данной формулы. (Ответ: -1; 15)
|
Учащиеся решают данное уравнение.
|
Проверка домашнего задания:
Деятельность учителя
|
Деятельность ученика
|
Ребята, дома вам было предложено решить 6 уравнений разного вида, которые решаются различными способами.
На доске в таблице 2, мы видим, отражено, кто сколько уравнений смог решить дома.
I уровень – обязательный минимум
II уровень – тренировочный
III уровень – творческое задание (вывешиваются на доску уравнения из домашнего задания, см. Приложения таблица 5).
Вызываются по 1 учащемуся к доске, обсуждаются решения предложенных уравнений и их комментирование.
Какие свойства или приемы решения данных уравнений вами использовались при решении уравнений?
Мы видим по таблице, заполненной вами, что не многим учащимся удалось решить уравнения III уровня. Давайте сегодня поговорим о таких уравнениях подробно.
Проблемная ситуация:
Можно ли свести к решению кв. уравнений, уравнения из домашнего задания и если можно, то как это сделать?
|
Решить биквадратное уравнение, заменив 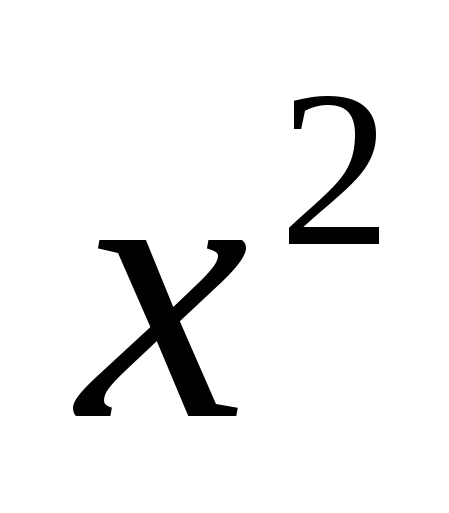 новой переменной (дается определение биквадратного уравнения) новой переменной (дается определение биквадратного уравнения)
Применить формулы сокращенного умножения, правила раскрытия скобок, свойства уравнения (перенос слагаемых из одной части в другую).
Нахождение общего знаменателя дробей.
Введение новой переменной.
Свойства уравнения (обе части уравнения умножить или разделить на одно и то же число, отличное от нуля).
|
Изучение нового материала:
Деятельность учителя
|
Деятельность ученика
|
Рассмотрим следующее уравнение: 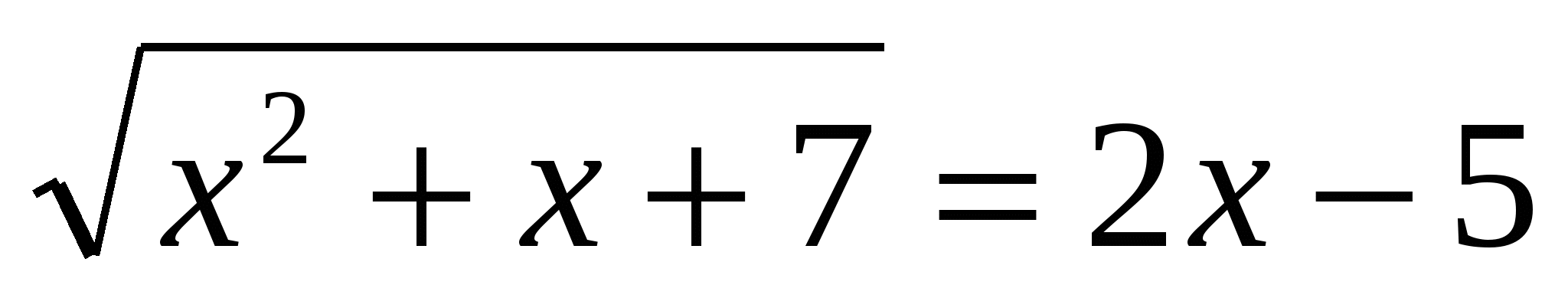 . .
Как видите, оно похоже на уравнение из домашнего задания III уровня. Их мы подробнее будем рассматривать и решать в 10 классе.
Дается определение иррационального уравнения: Уравнения, содержащие переменную под знаком радикала, называются иррациональными.
Метод решения таких уравнений состоит в том, что, оставляя радикал в одной части уравнения, возводят обе части уравнения в соответствующую степень до тех пор, пока не получится уравнение, не содержащее радикалов и поскольку, могут появиться «посторонние» корни, то необходимо выполнить проверку найденных корней с помощью подстановки.
Вводится понятие «посторонних» корней. ( Корни уравнения, не удовлетворяющие исходному уравнению, называются посторонними).
Вернемся к таблице 1, рассмотрим этапы решения уравнений:
Дайте определение арифметического квадратного корня.
Т.е. какое выражение в данном случае должно быть неотрицательным?
Поэтому запишем это условие: 2х - 5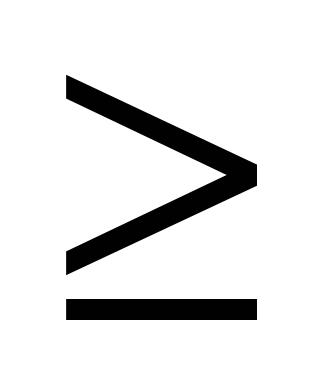 0 0
Что представляет из себя левая часть данного уравнения?
Когда определен квадратный корень из числа?
Значит, какое выражение должно быть неотрицательным?
Как это записать?
В какую степень нужно возвести обе части уравнения, чтобы избавиться от знака радикала?
Имеем: 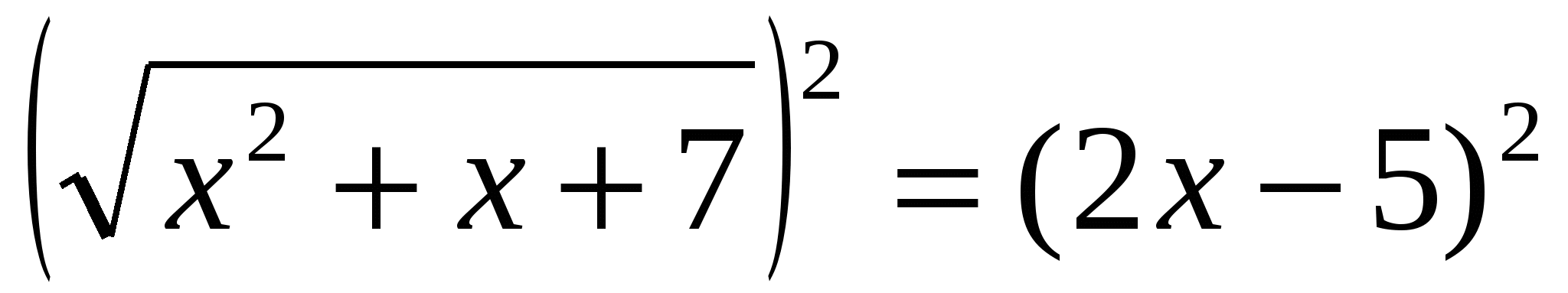
Удобнее все полученные выражения записывать в виде системы:
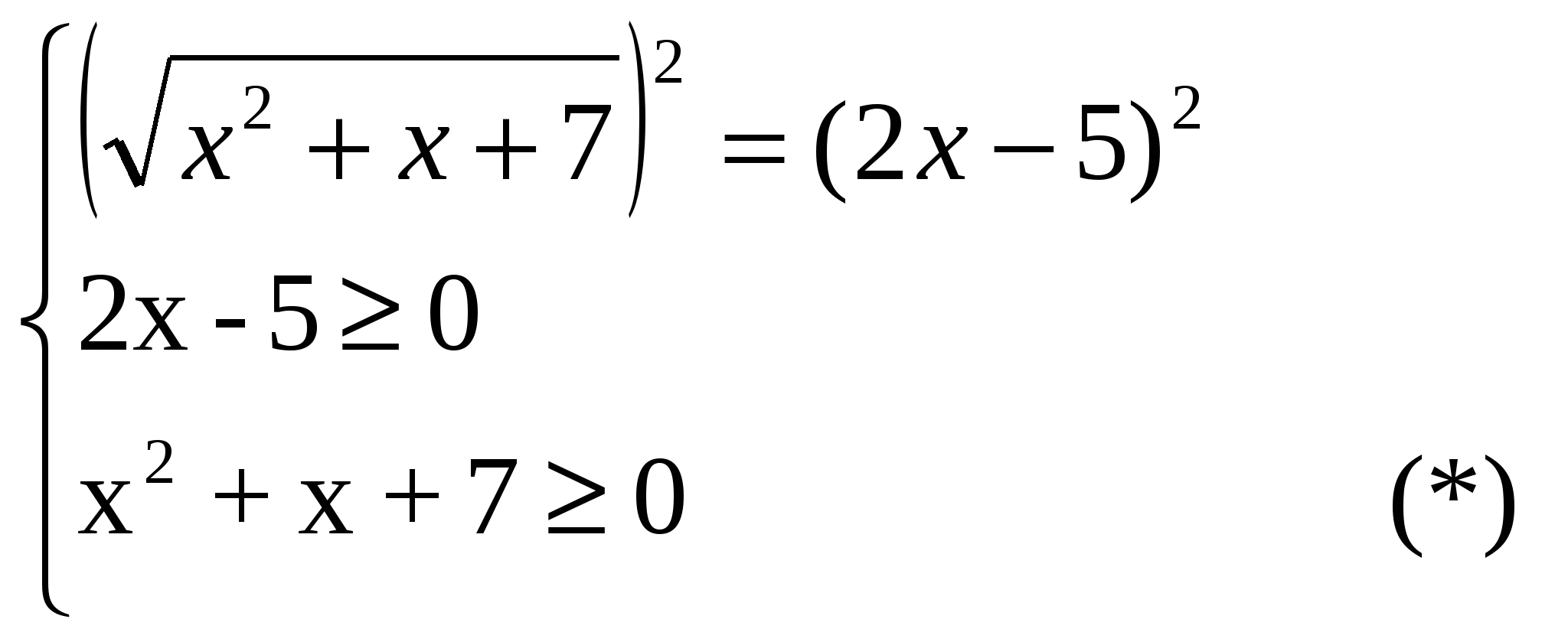
Неравенство (*) верно при любых значениях переменной х, значит
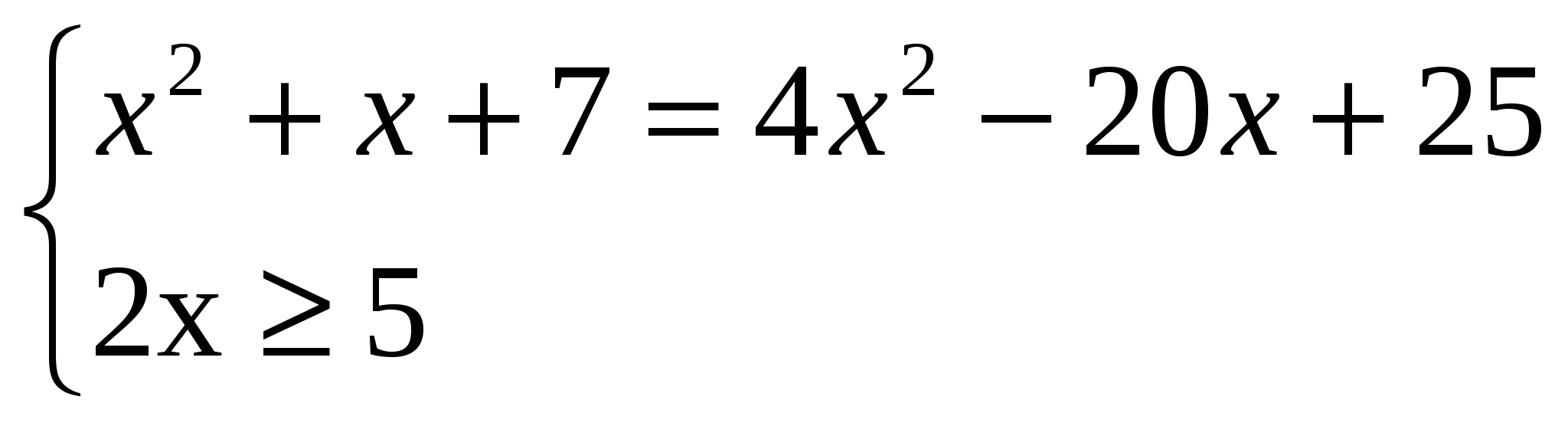 , ,
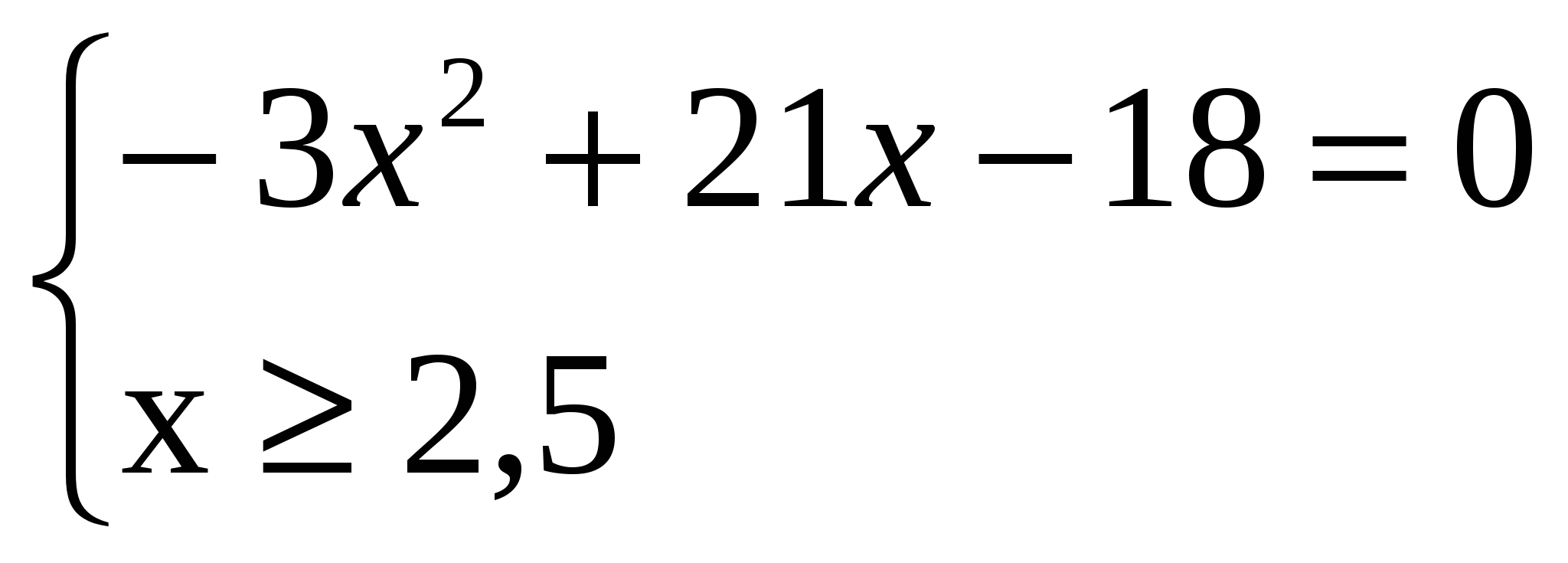 , ,
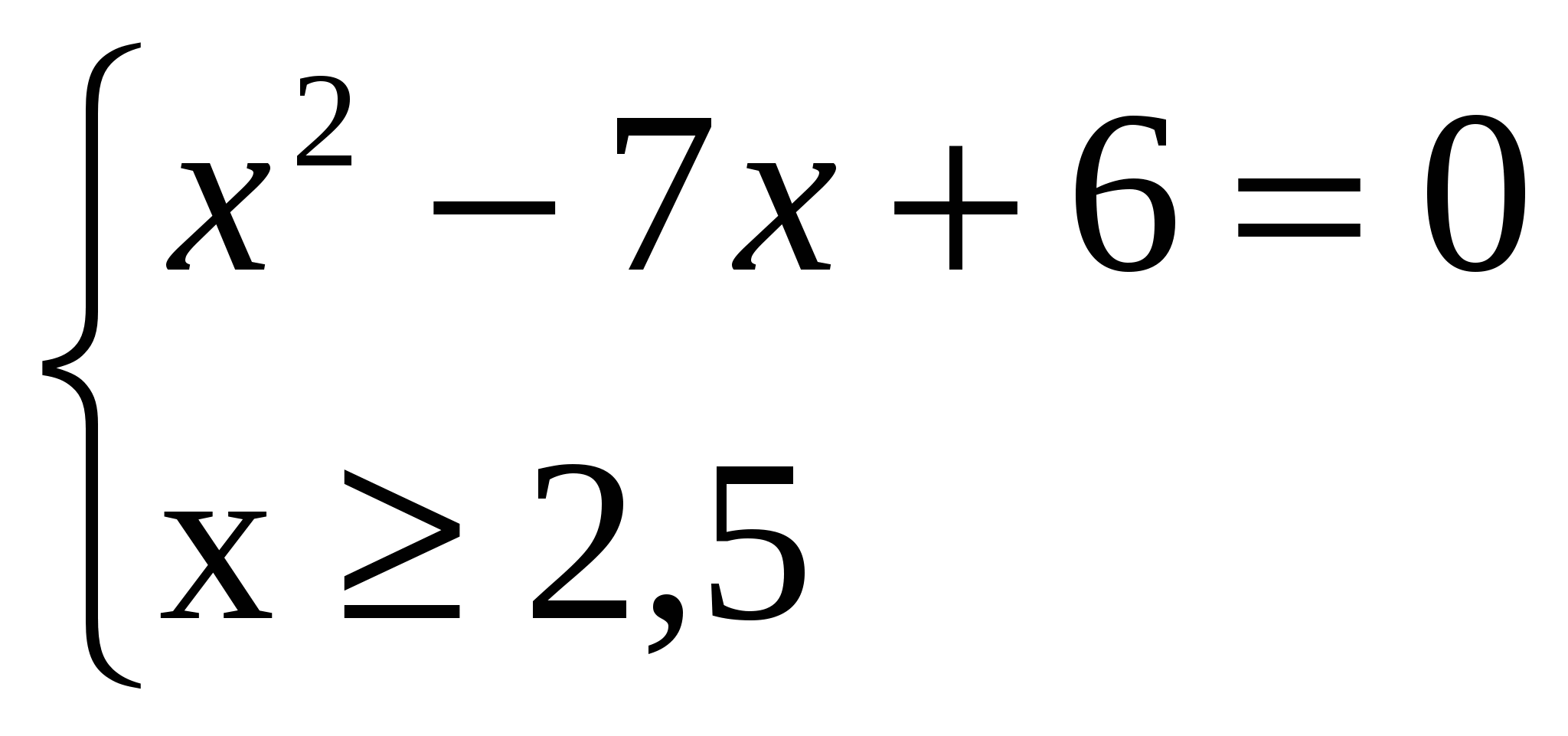 , ,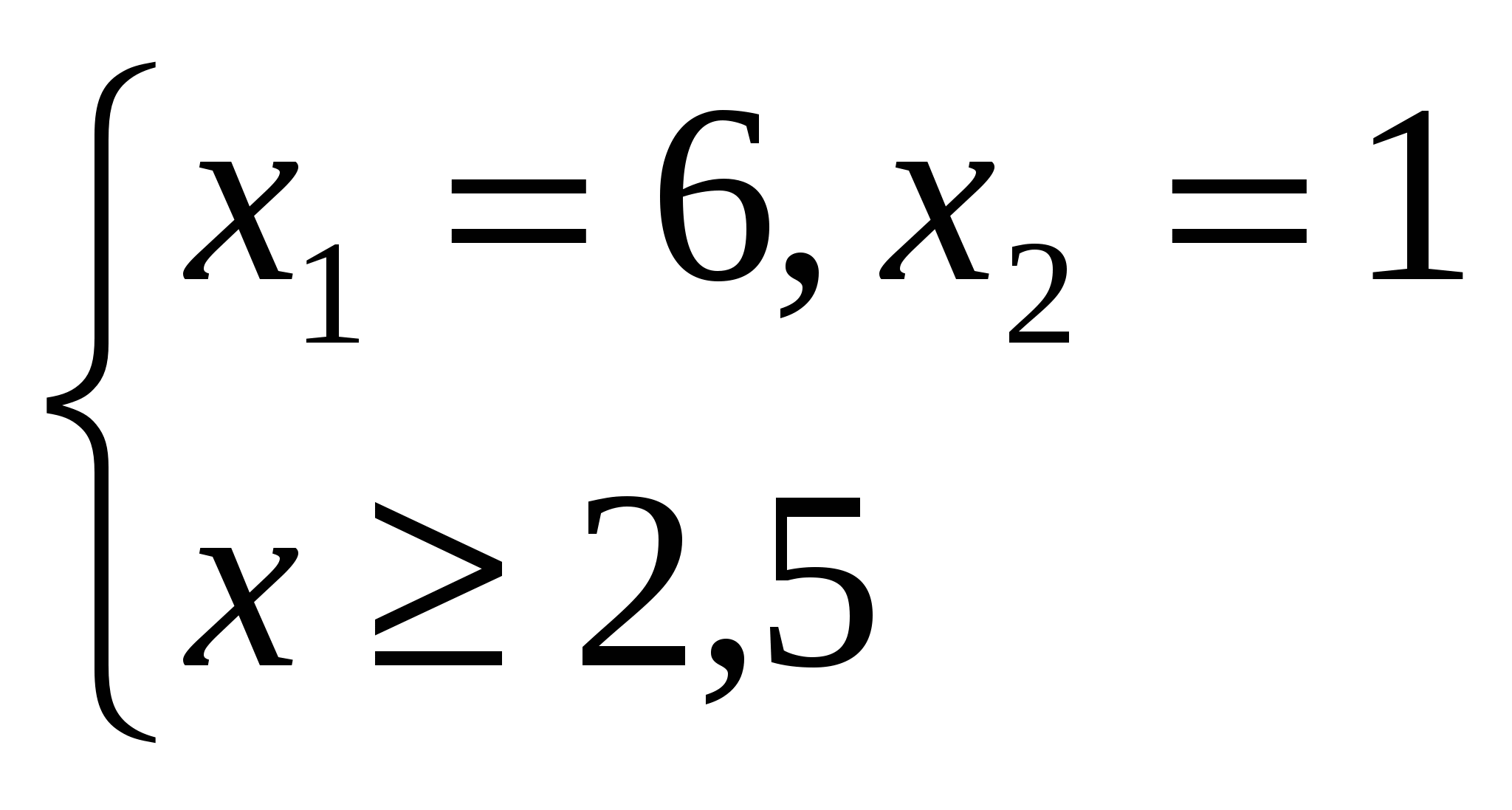
6  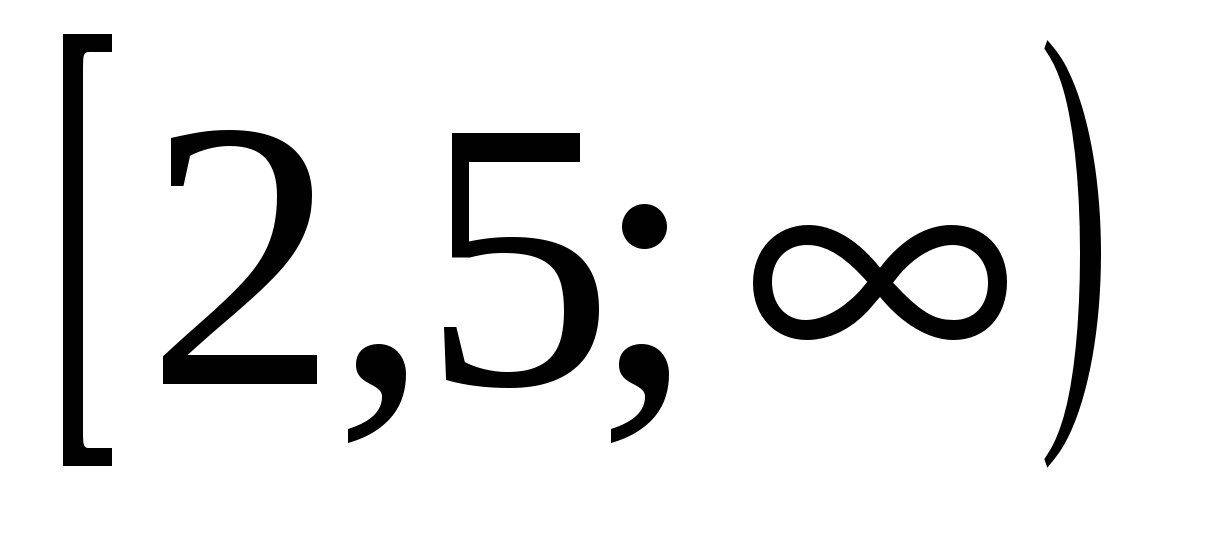
1  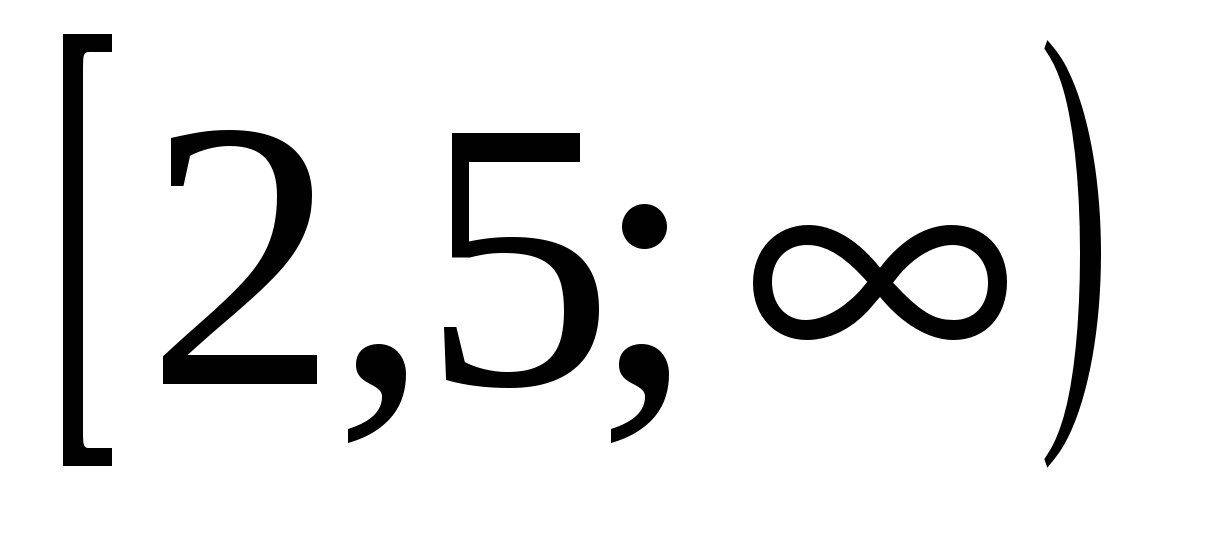
Проверкой можно также убедиться, что число 1 не является корнем уравнения.
Ответ: 6
|
Учащиеся записывают определение.
Учащиеся записывают определение.
Арифметическим квадратным корнем из числа a называется неотрицательное число, квадрат которого равен a.
2х – 5
Учащиеся пишут в тетради.
Квадратный корень (или знак радикала).
Квадратный корень из числа определен, если подкоренное выражение неотрицательно.
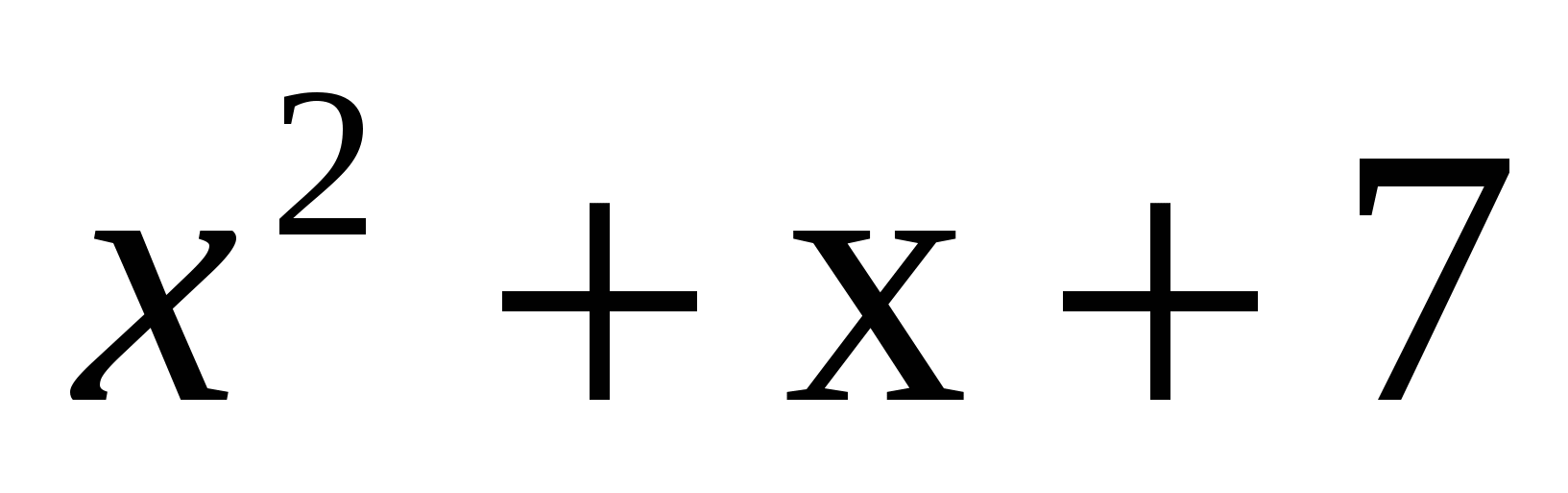
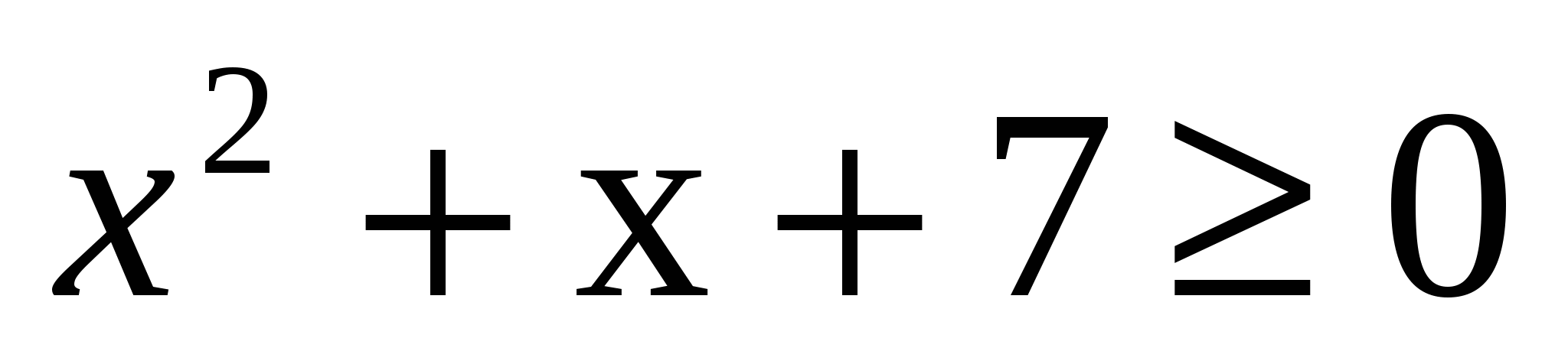
Во вторую.
Решает у доски 1 ученик при помощи учителя.
Учащиеся помогают выполнить подстановку, диктуя решение устно, с места.
|
Закрепление изученного материала:
Класс разбивается на 2 группы. Предлагается решить уравнение 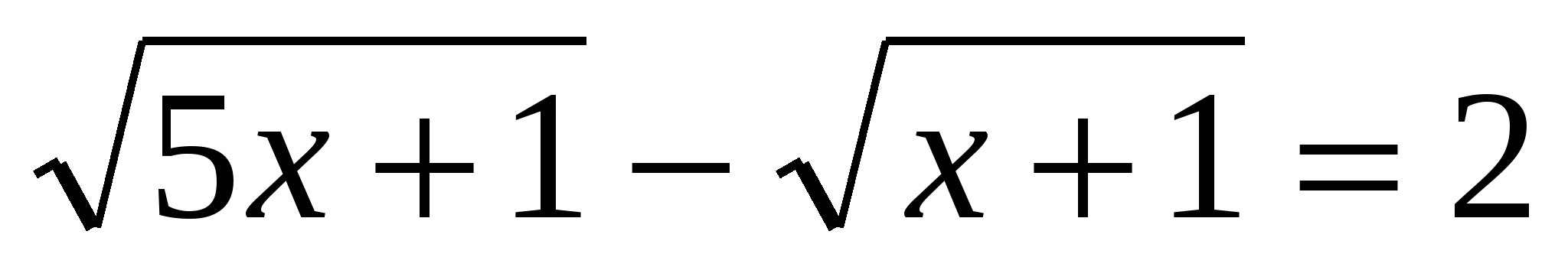 двумя способами. двумя способами.
Деятельность учителя
|
Деятельность ученика
|
Какой способ на ваш взгляд является более рациональным?
Все ли корни полученного квадратного уравнения являются решениями?
Вернемся к домашнему заданию. Можно ли уравнения III группы решить предложенными способами?
Итак, мы обнаружили, что к решению квадратных уравнений сводятся и некоторые иррациональные.
|
I способ:
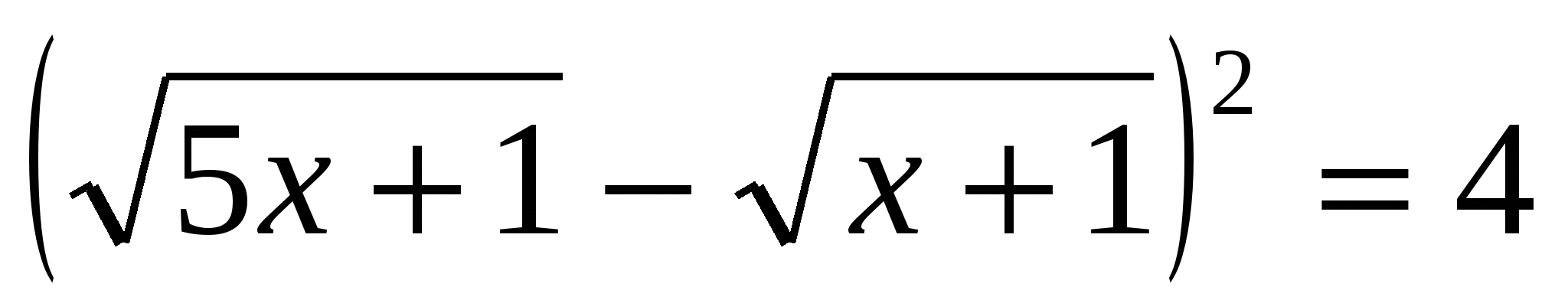
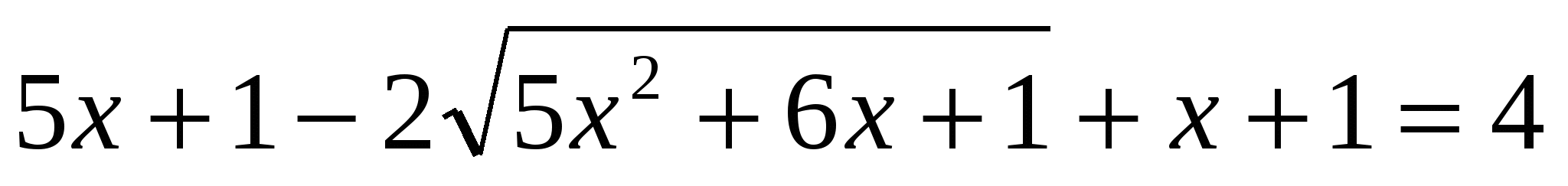
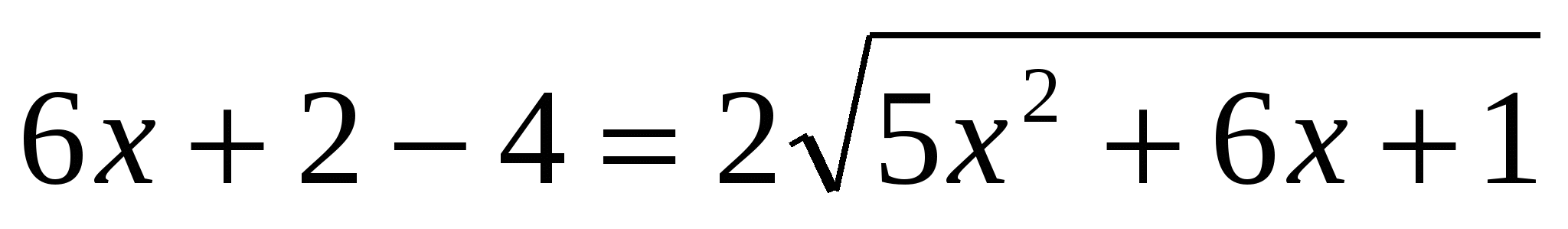
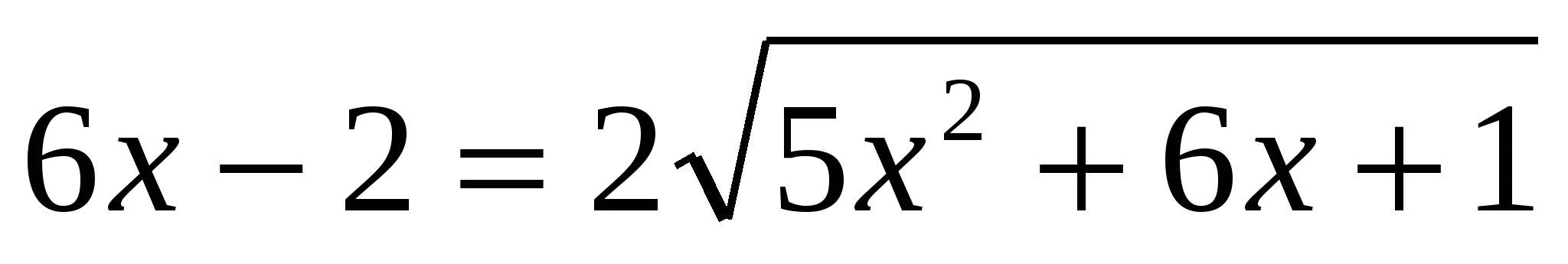
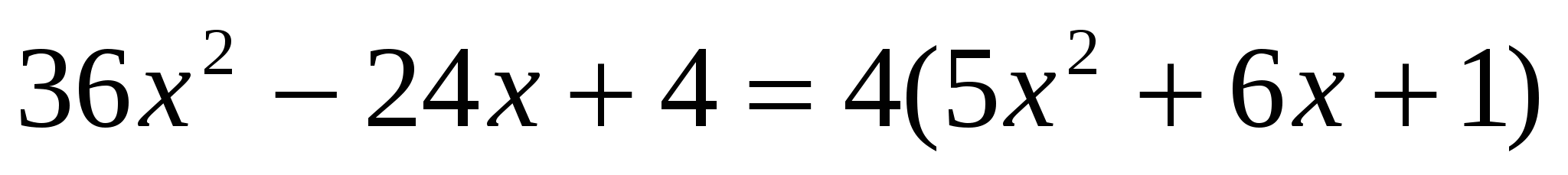
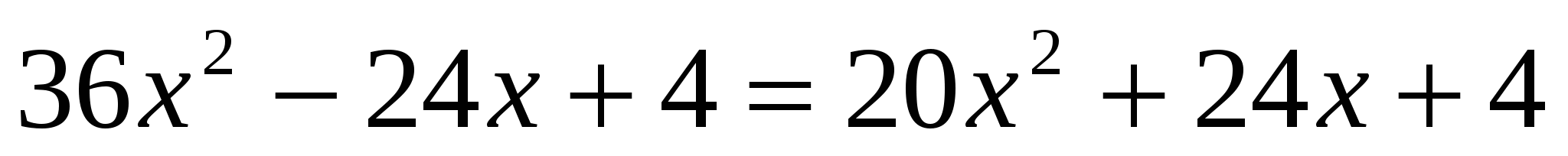
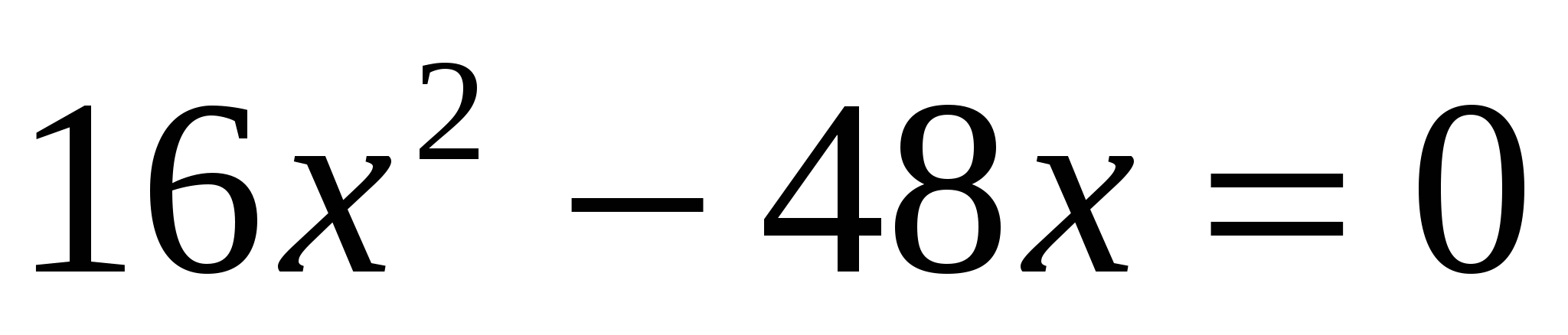
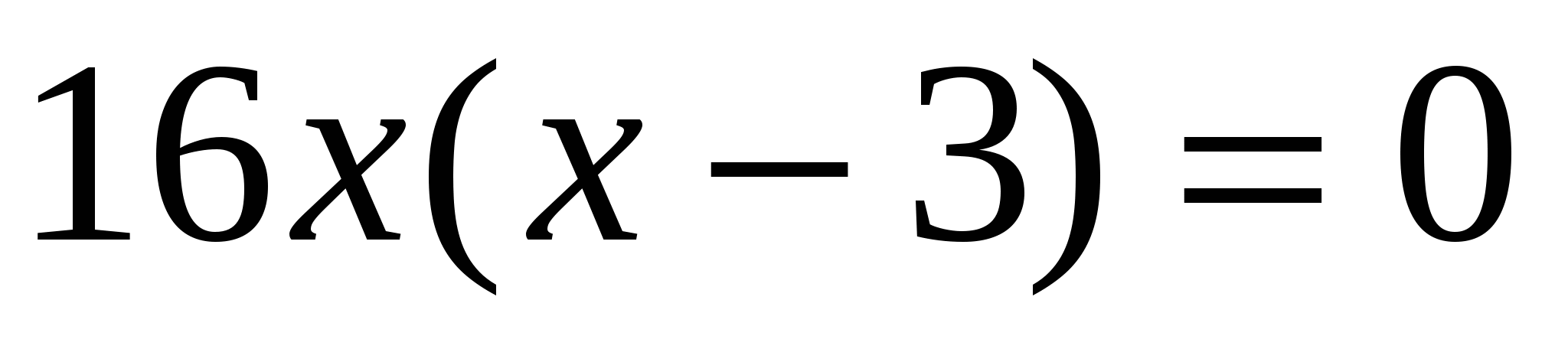
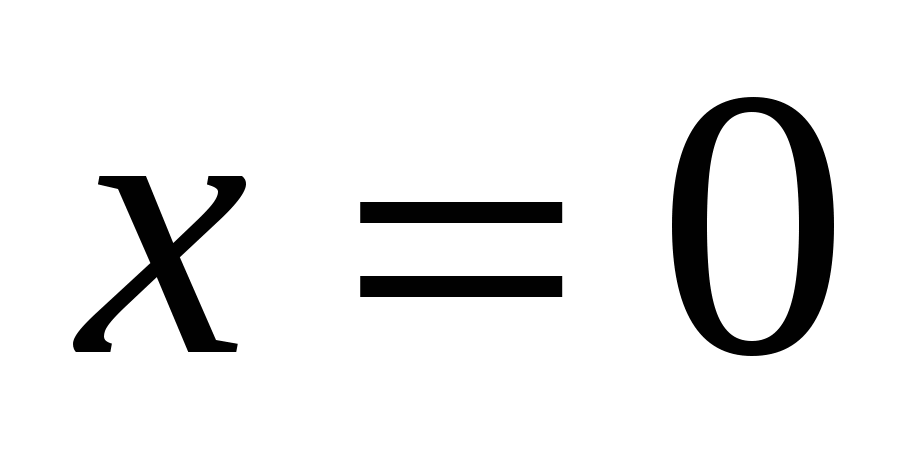 или или 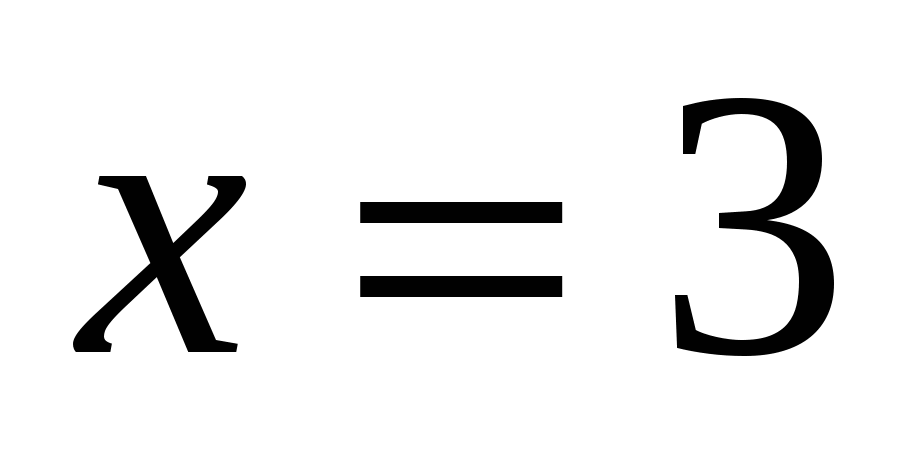
Проверка: 0 – не является корнем.
Ответ: 3.
II способ:
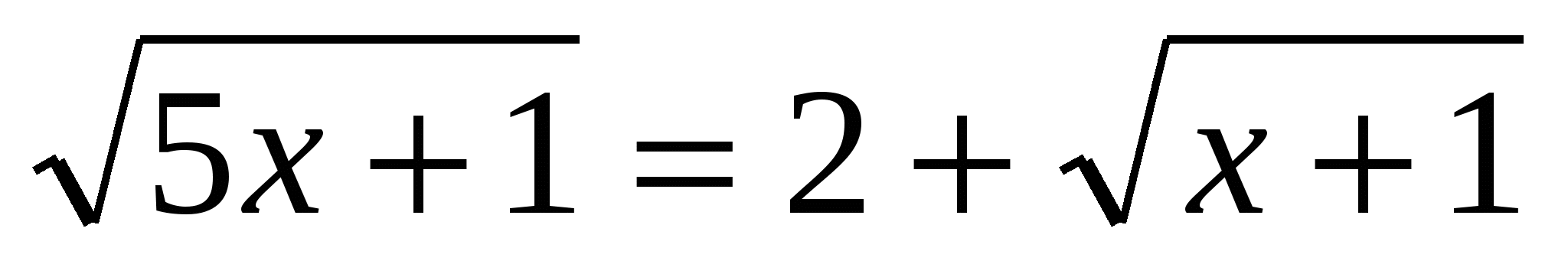
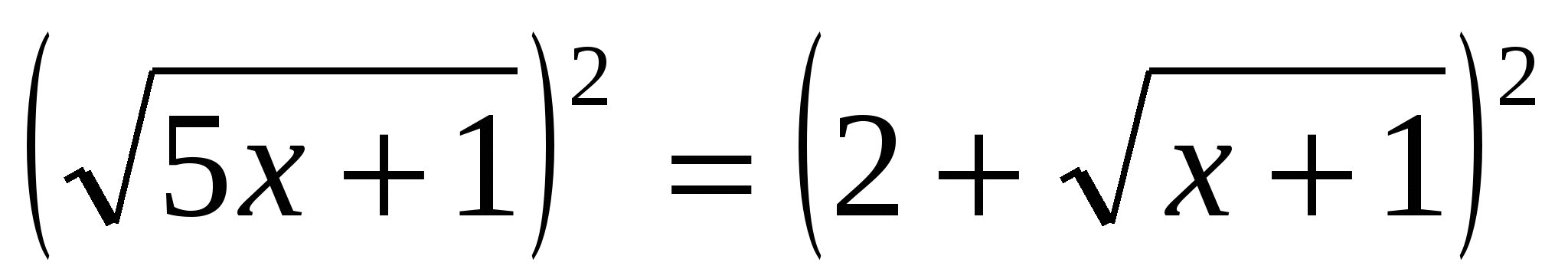
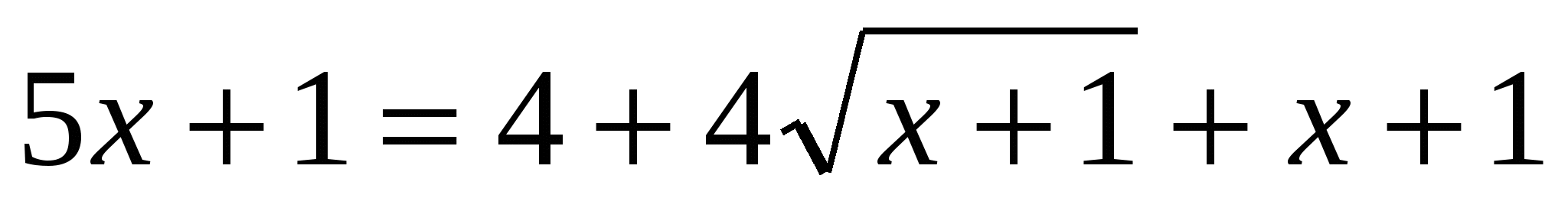
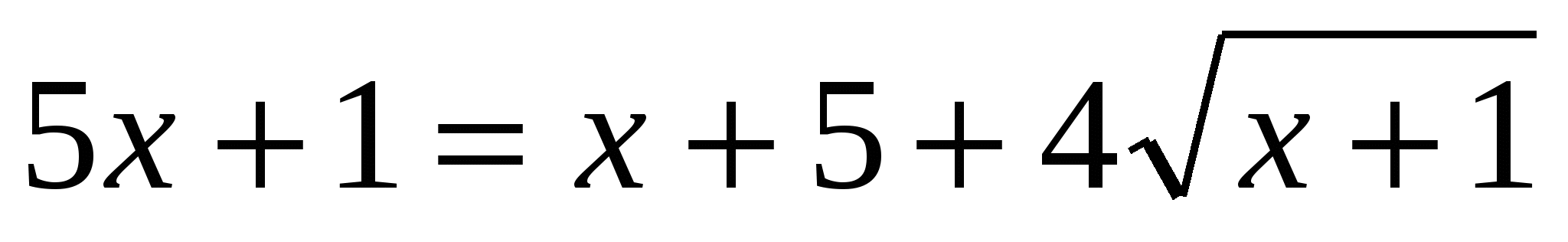
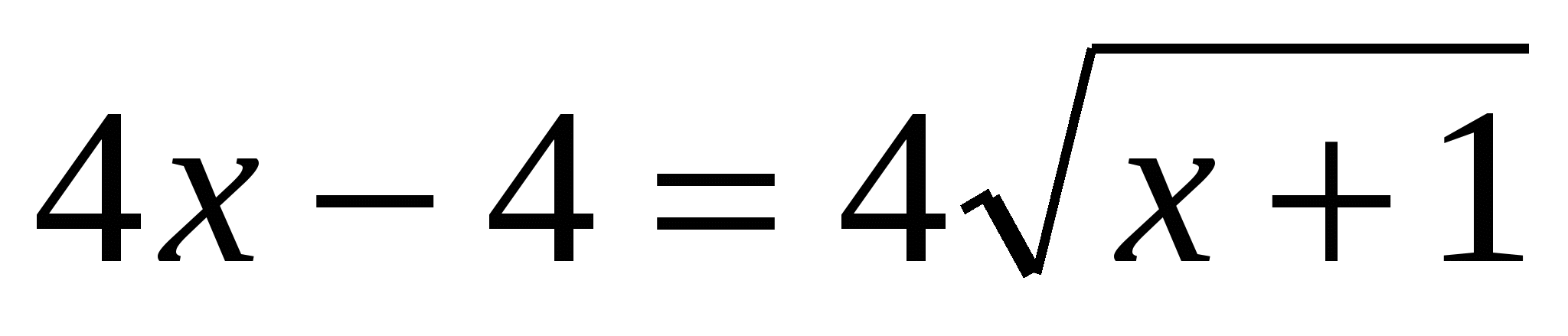
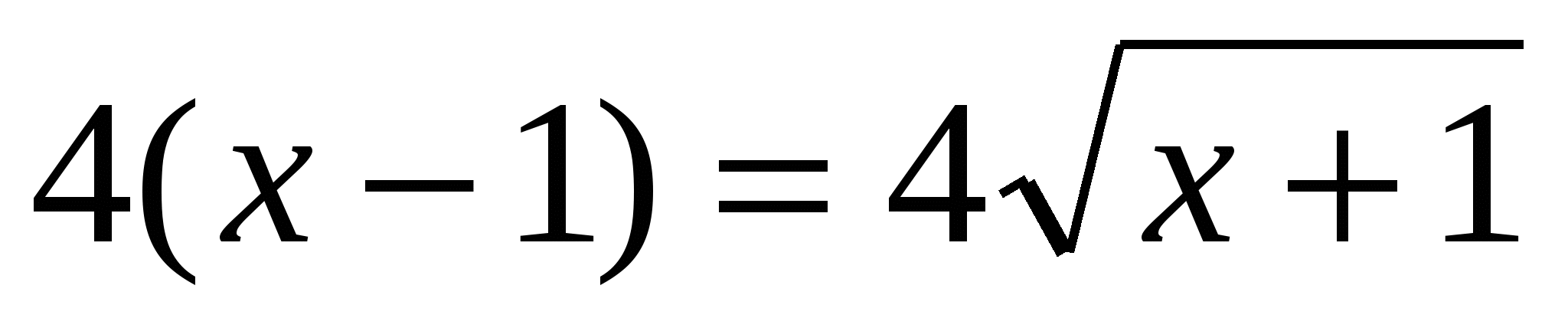
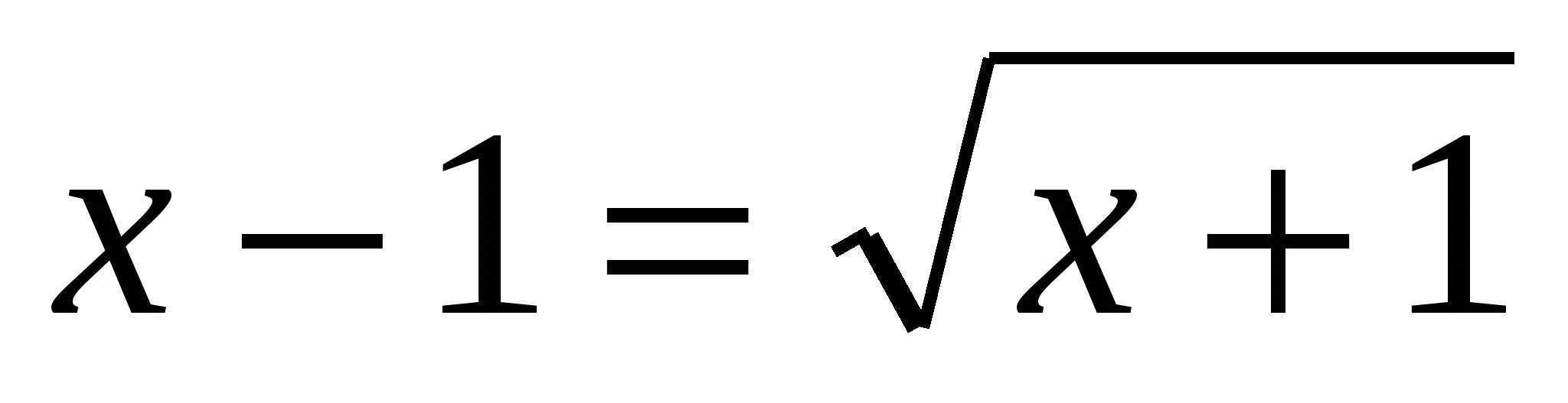
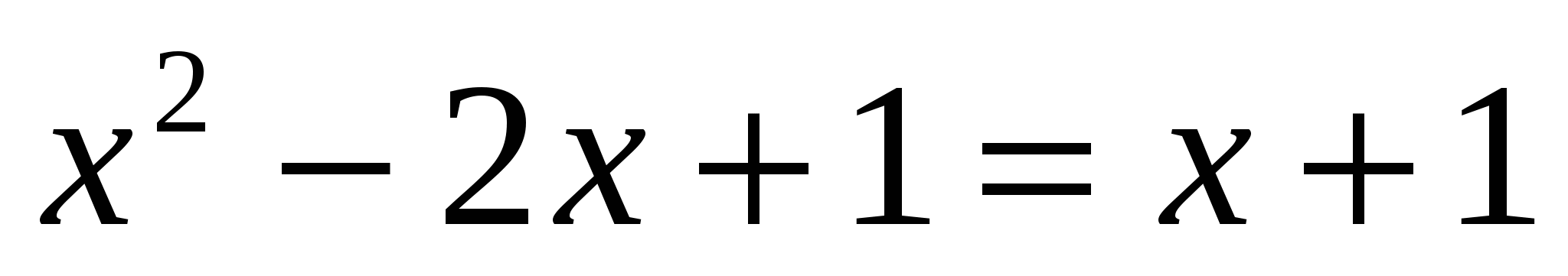
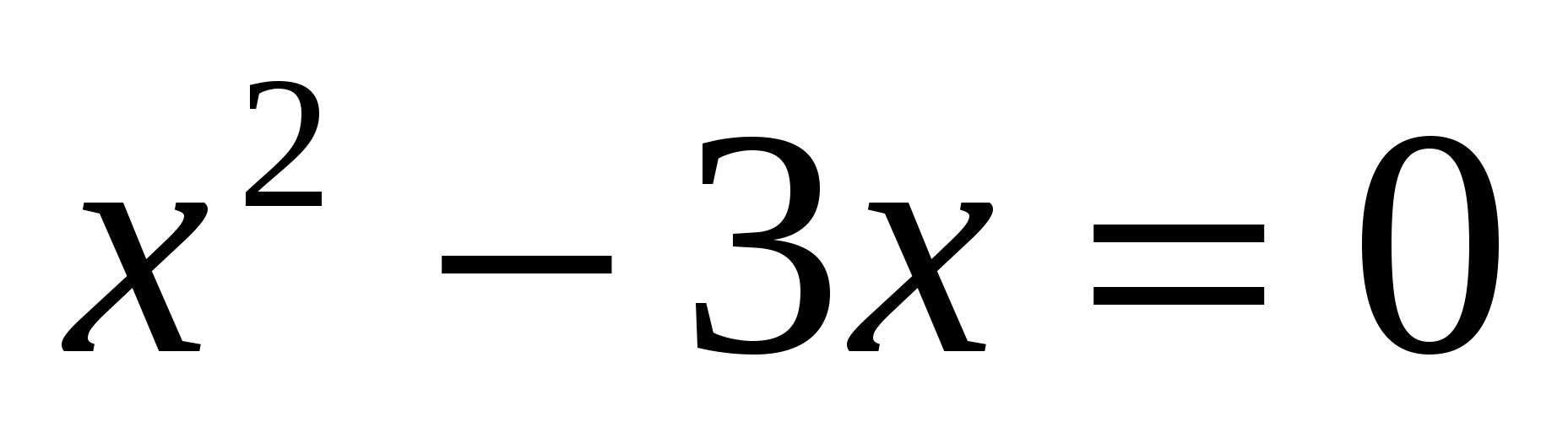
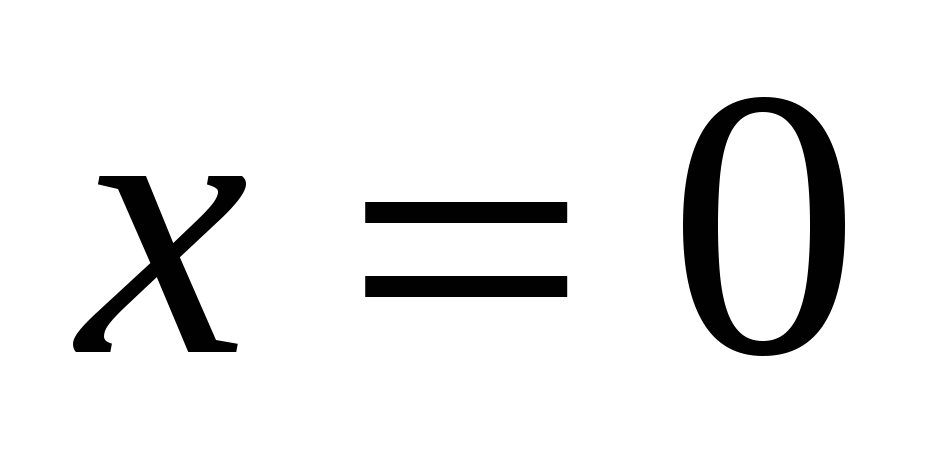 или или 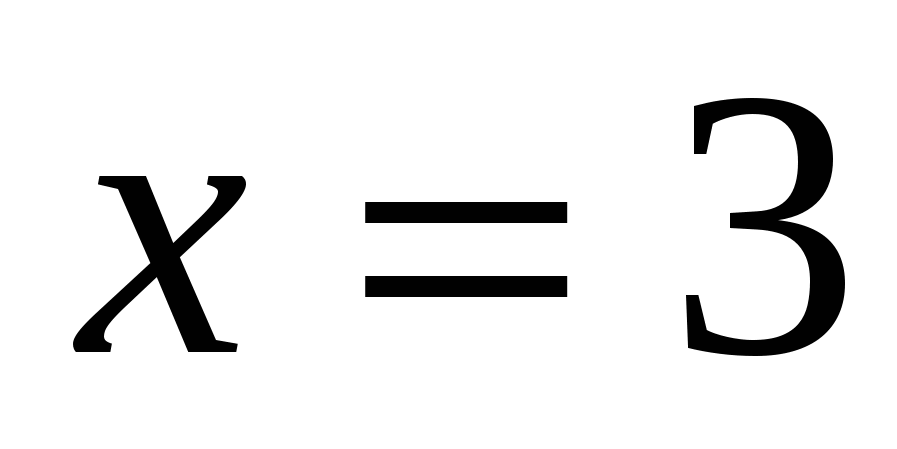 . .
Проверка.
Ответ: 3.
Второй способ.
Нет.
Да.
|
Отработка знаний, умений, навыков:
Задания у каждого ученика на отдельном печатном листе.
Решите уравнения, запишите корни последовательно в строчку, воспользовавшись ключом к шифру и узнайте оценку вашего труда (дети разбиваются на 6 групп; каждой группе дается по одному уравнению.)
Ключ:
1
|
2
|
3
|
4
|
5
|
6
|
х
|
о
|
о
|
ш
|
о
|
р
|
7
|
1
|
1
|
20
|
1
|
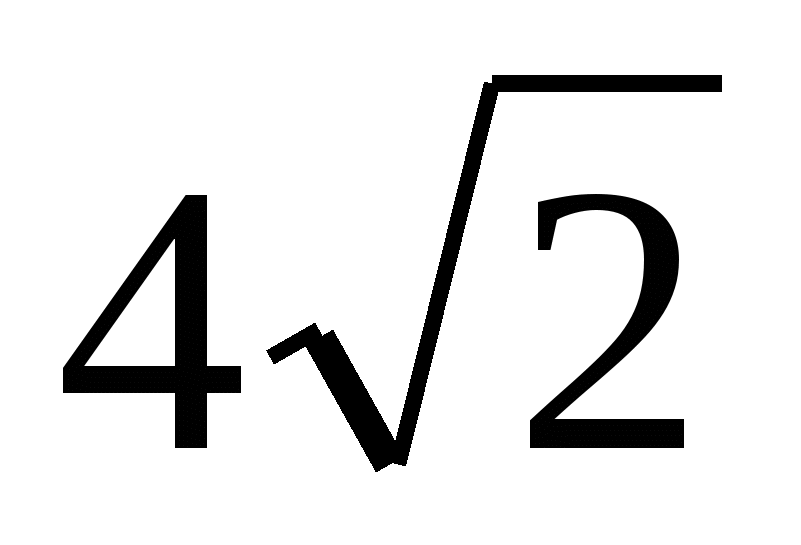
|
1 – «о»
20 – «ш»
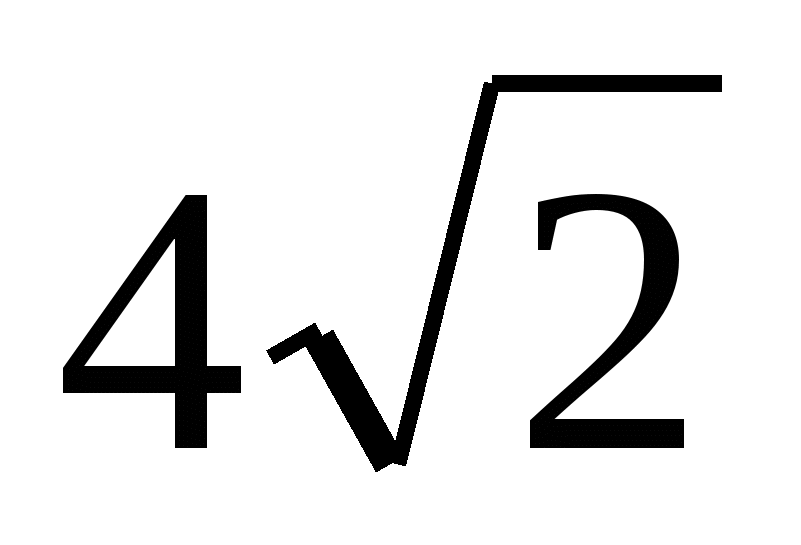 - «р» - «р»
«хорошо»
Деятельность учителя
|
Деятельность ученика
|
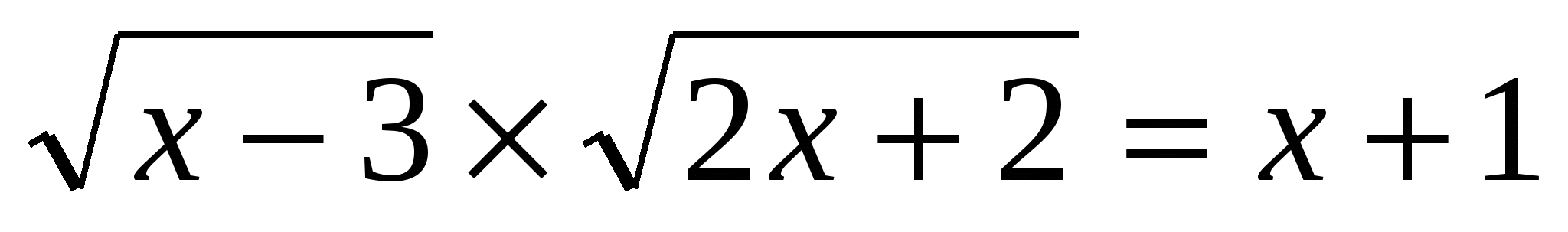 (Ответ: 7) (Ответ: 7)
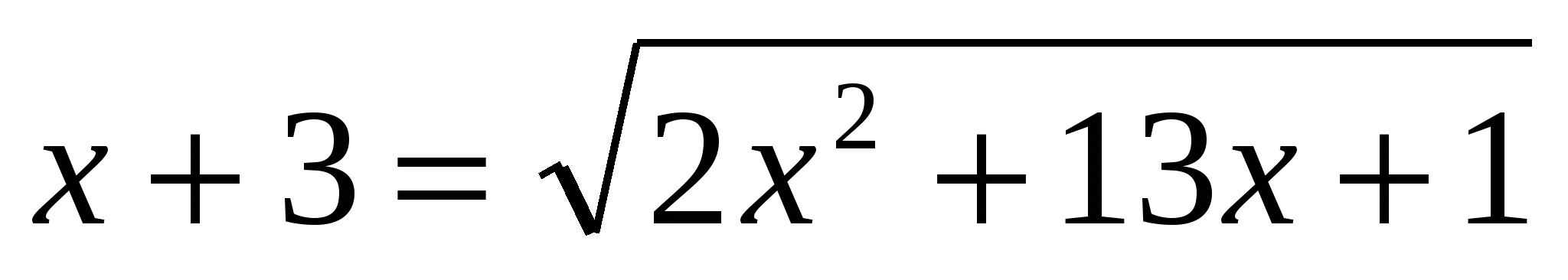 (Ответ: 1) (Ответ: 1)
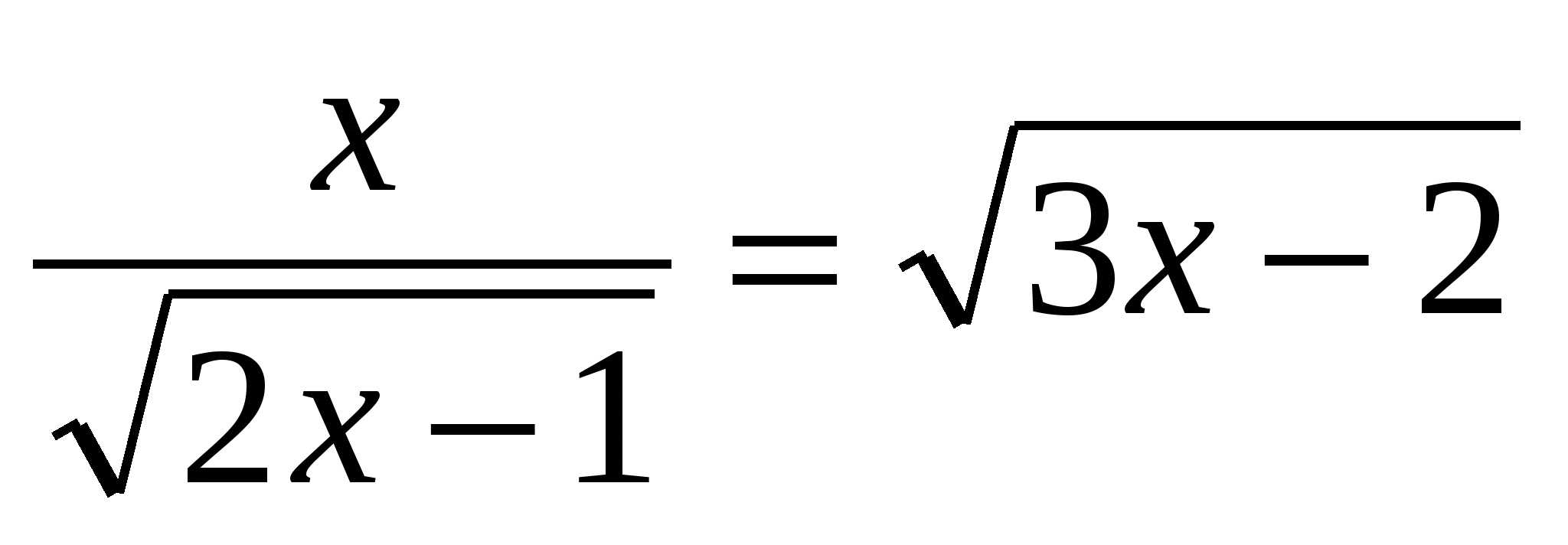 (Ответ: 1) (Ответ: 1)
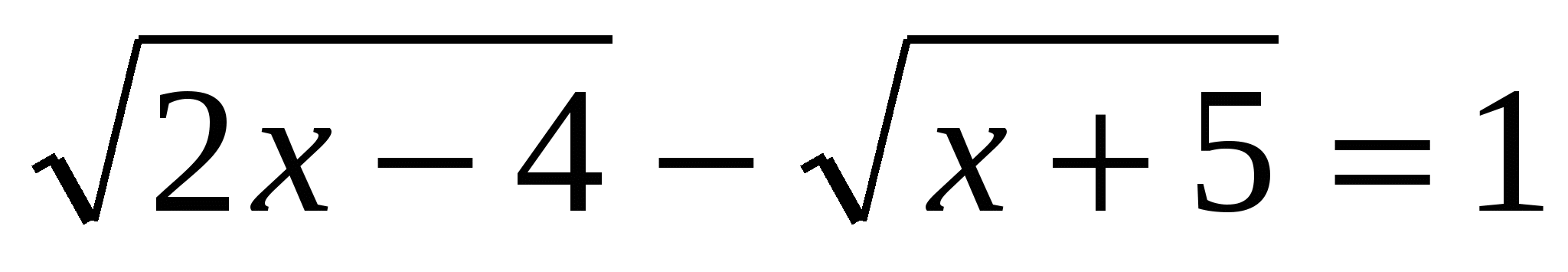 (Ответ: 20) (Ответ: 20)
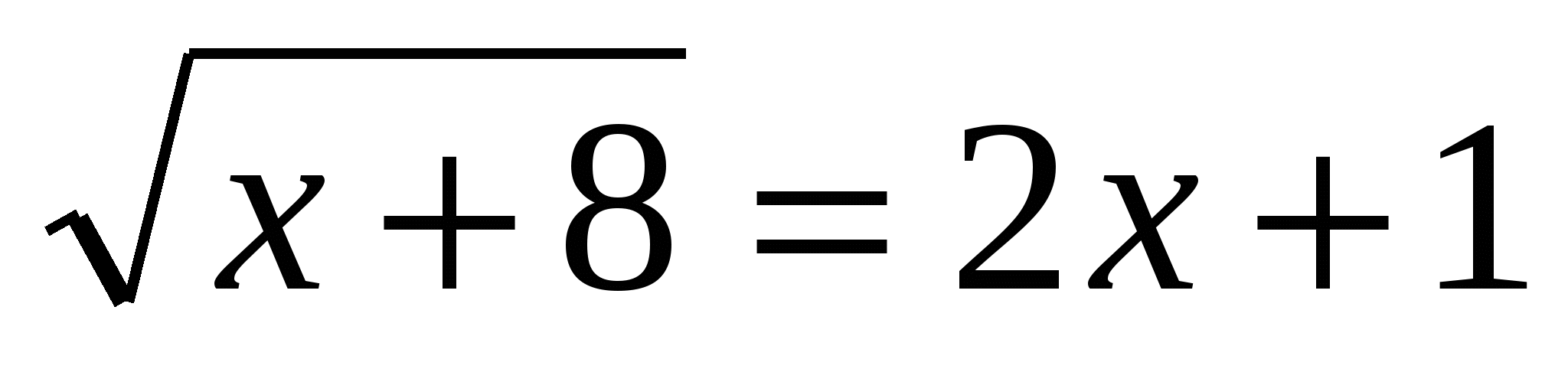 (Ответ: 1) (Ответ: 1)
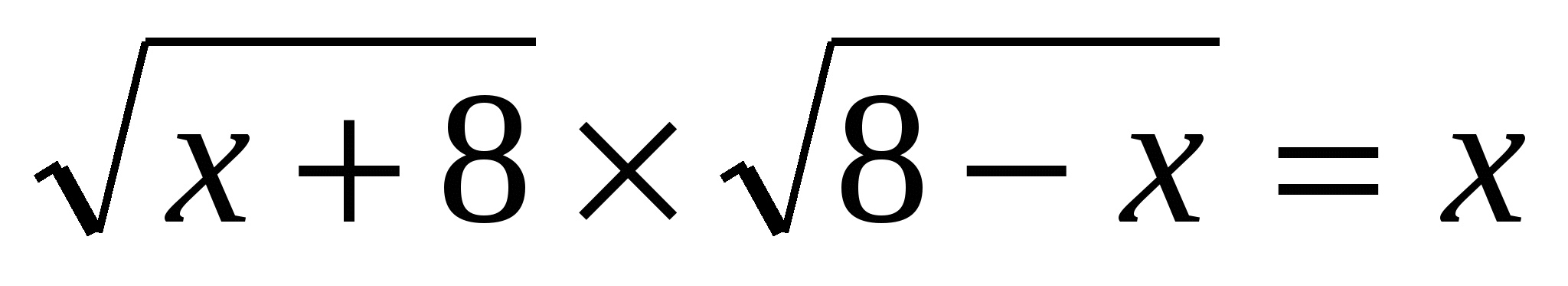 (Ответ: (Ответ: 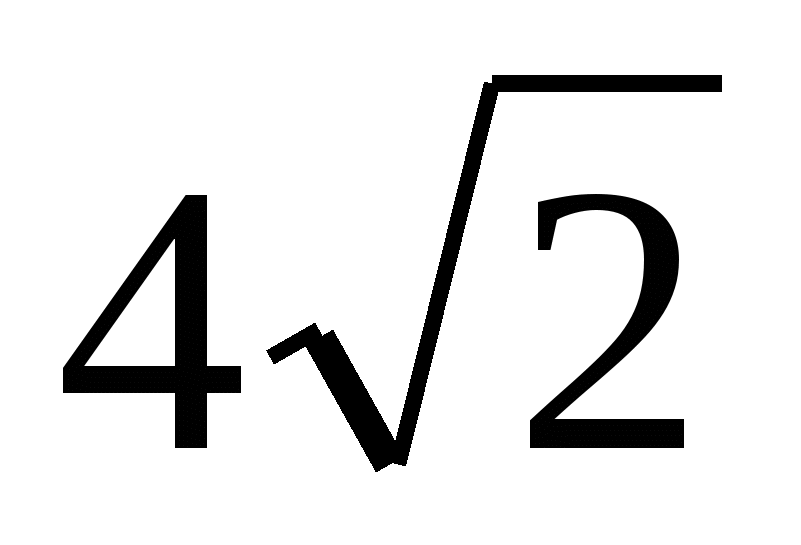 ) )
Итак, ребята, сегодня вы познакомились с новым видом уравнений, которые можно решать с помощью квадратных уравнений. Оставшиеся на листочке уравнения будут вашим домашним заданием.
|
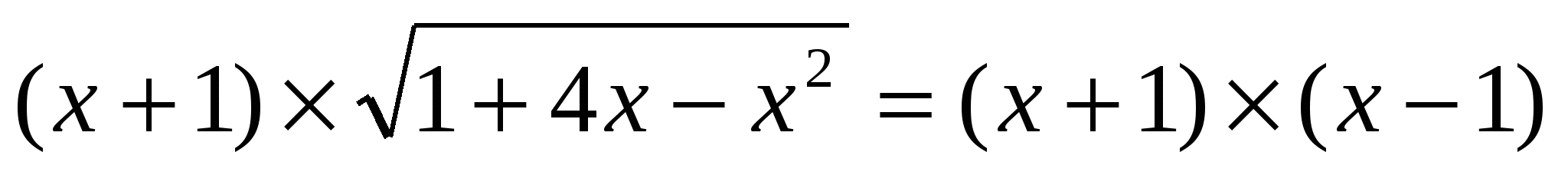
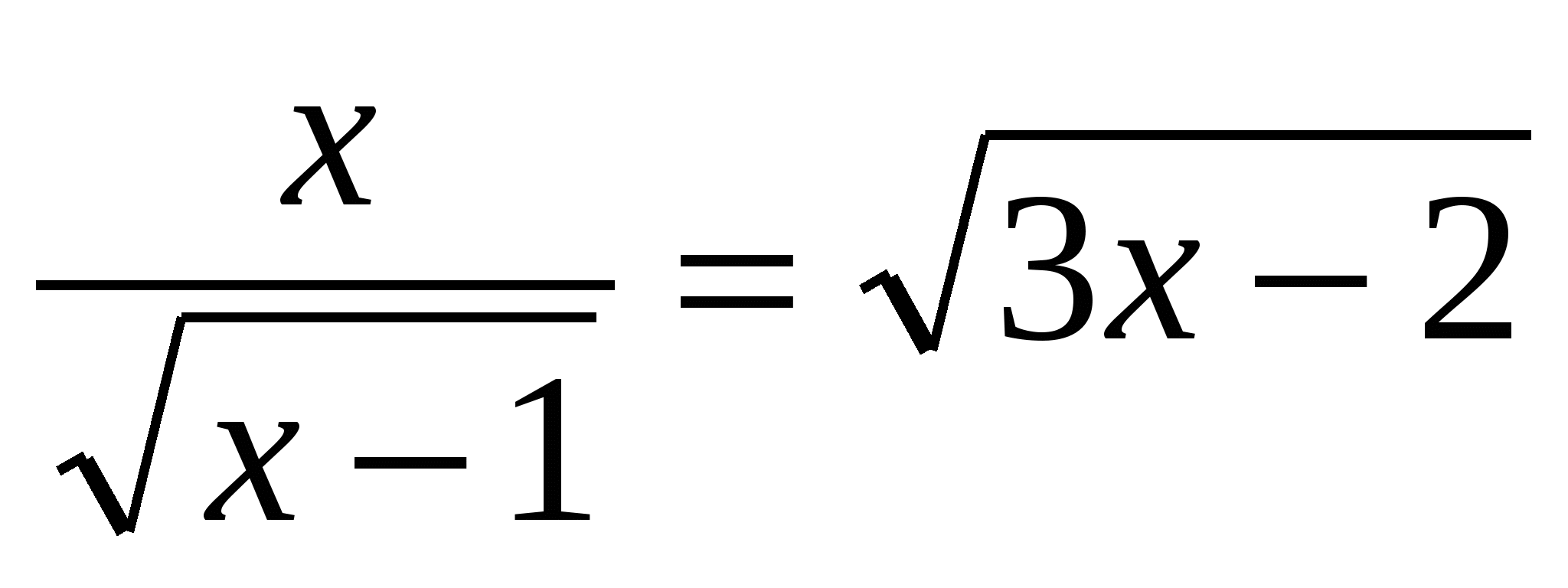
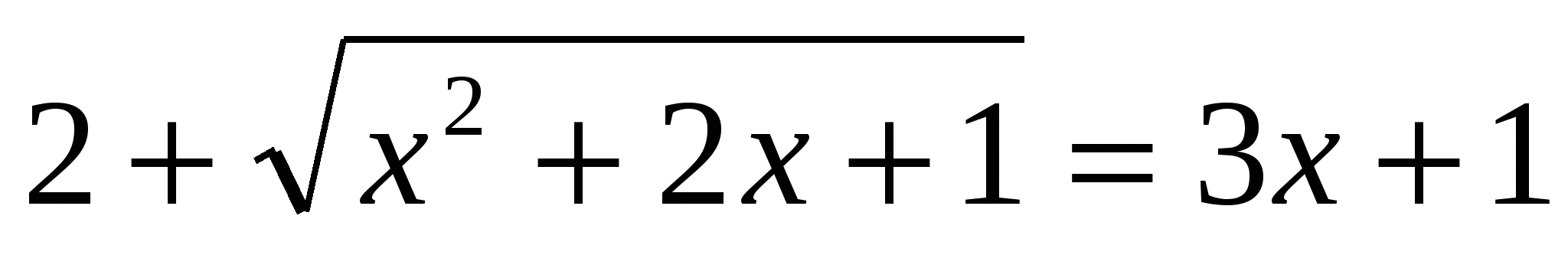
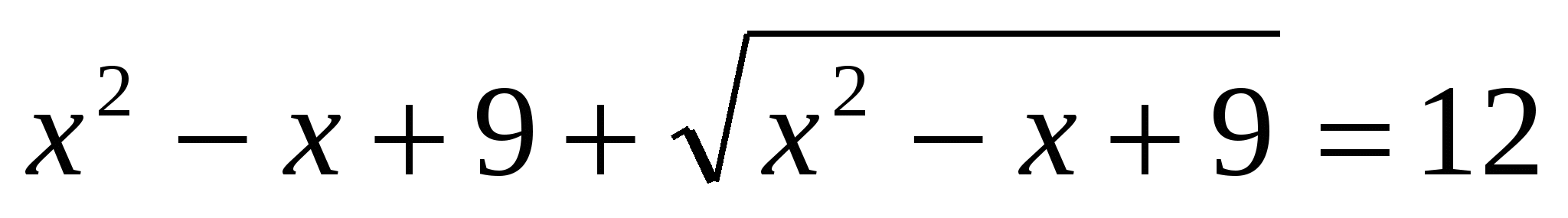
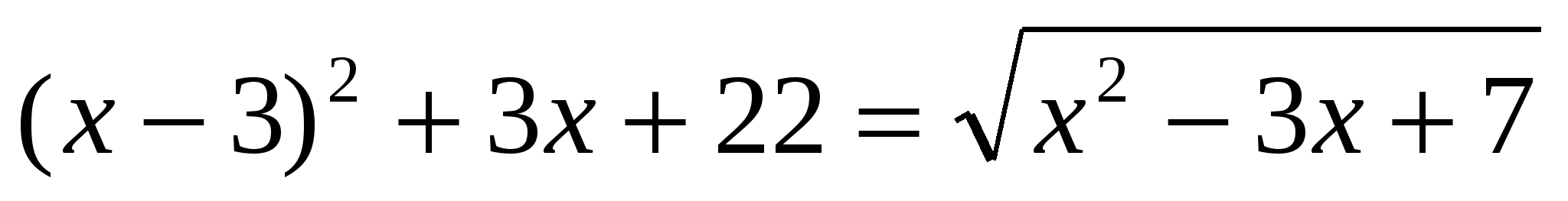
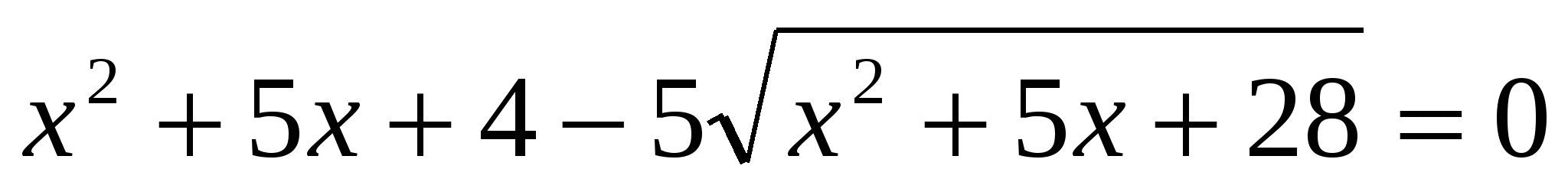
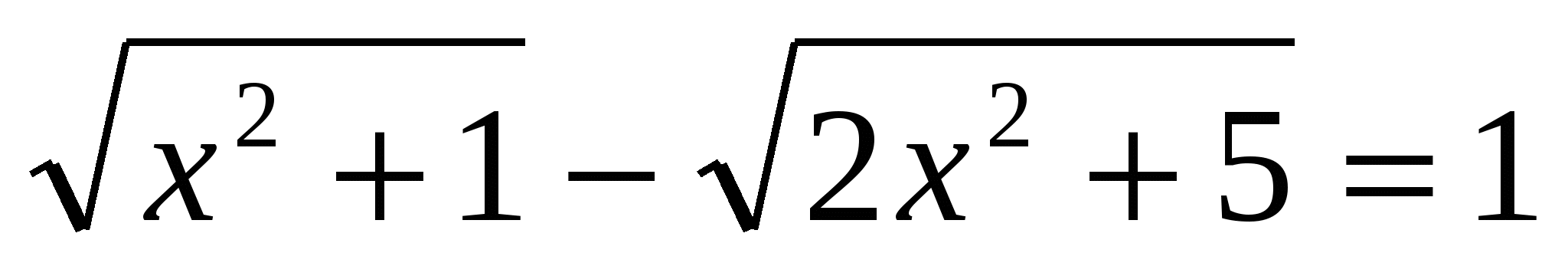
|
Итог занятия:
Деятельность учителя
|
Деятельность ученика
|
Поставьте по 10-бальной системе оценку за свою работу, обоснуйте.
Спасибо, дети, за прекрасную работу на занятии. До встречи.
|
Дети ставят оценку на отдельный листочек и результаты сдают учителю.
| |
|
|
 Скачать 98.74 Kb.
Скачать 98.74 Kb.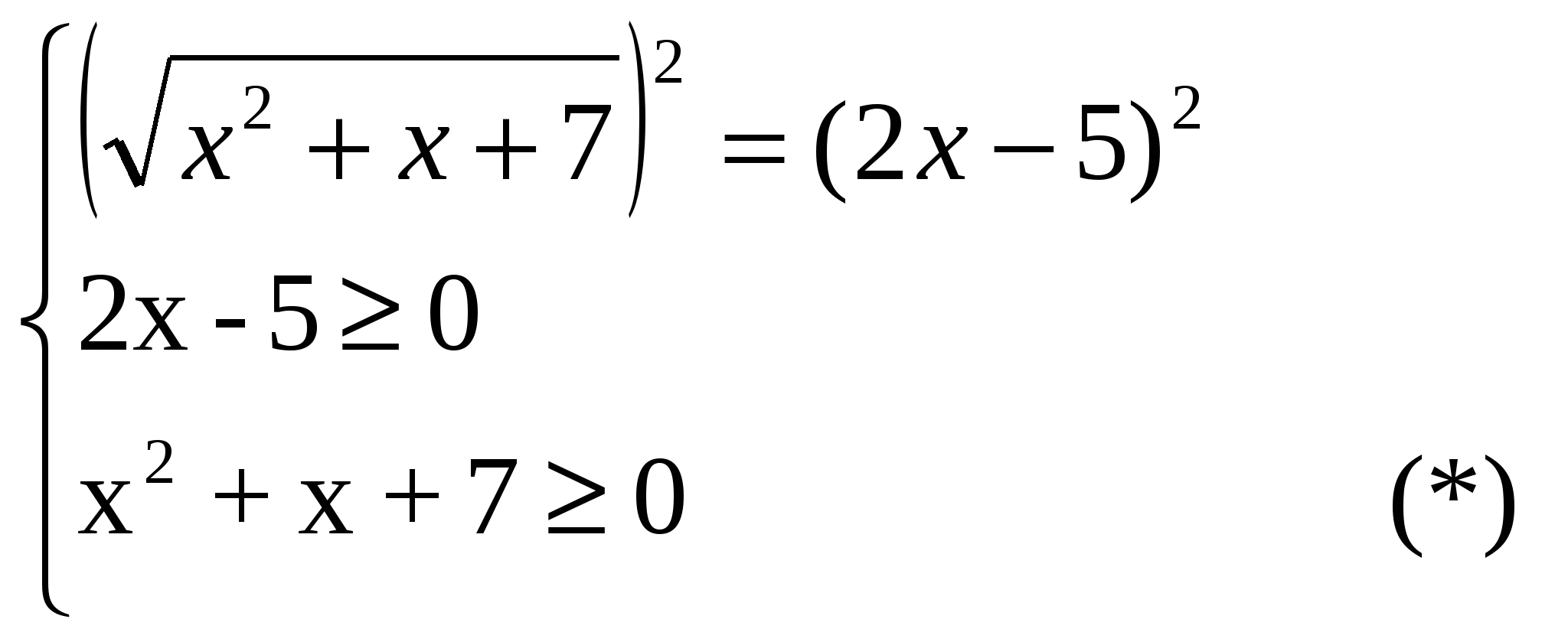
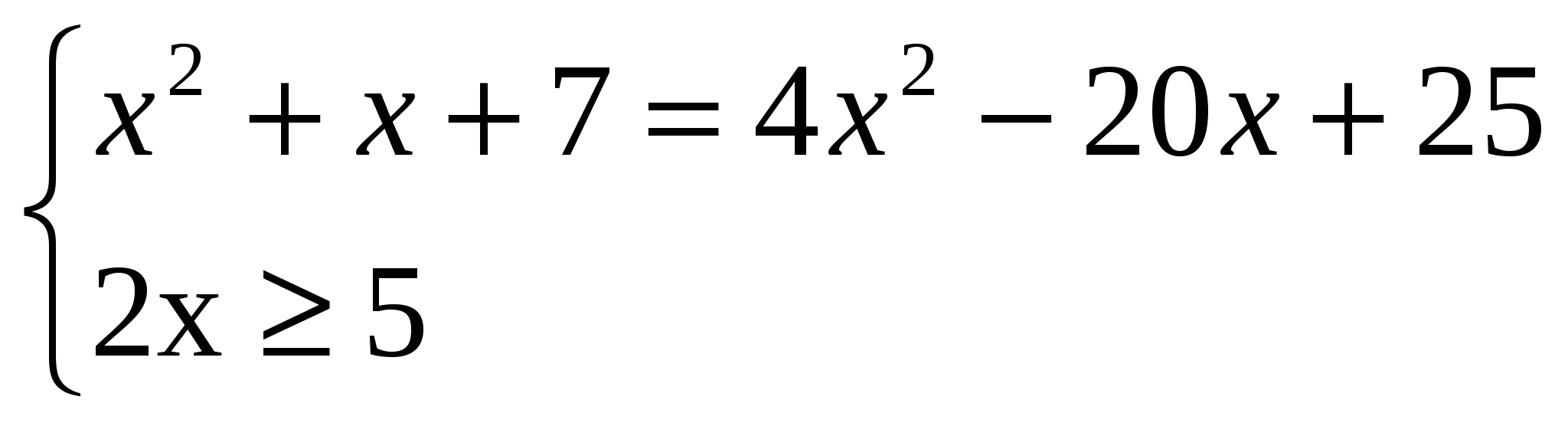 ,
,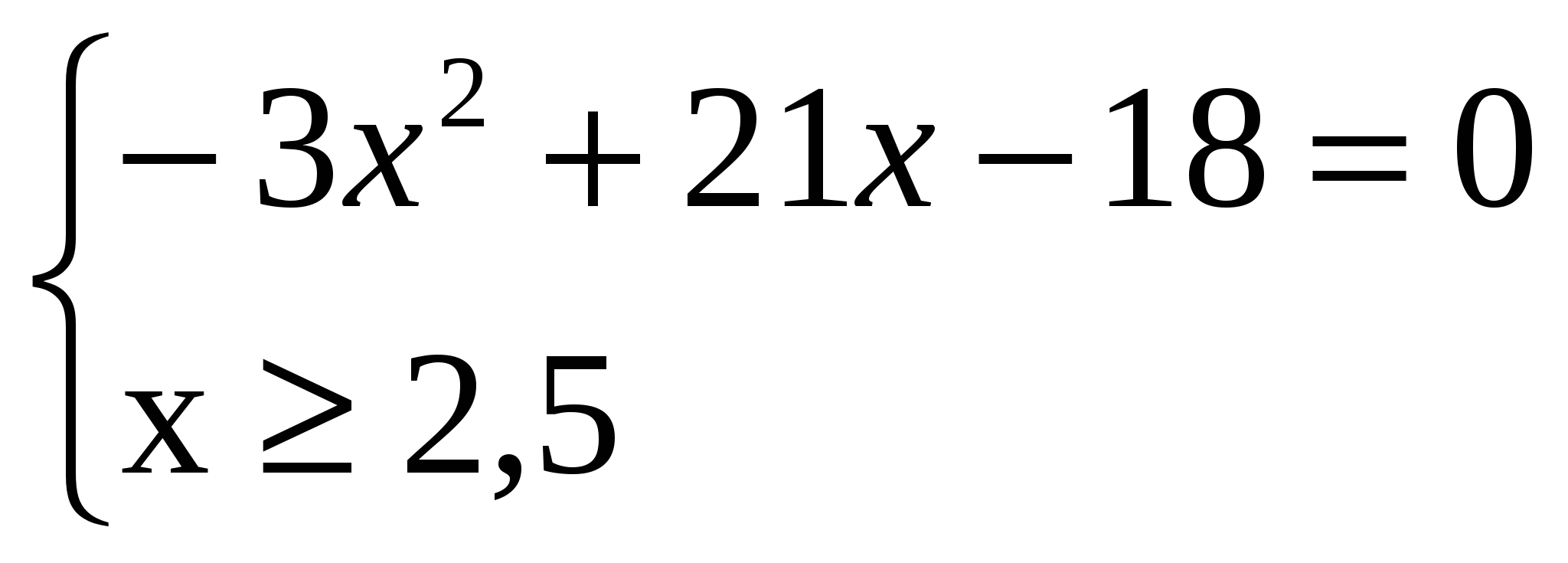 ,
,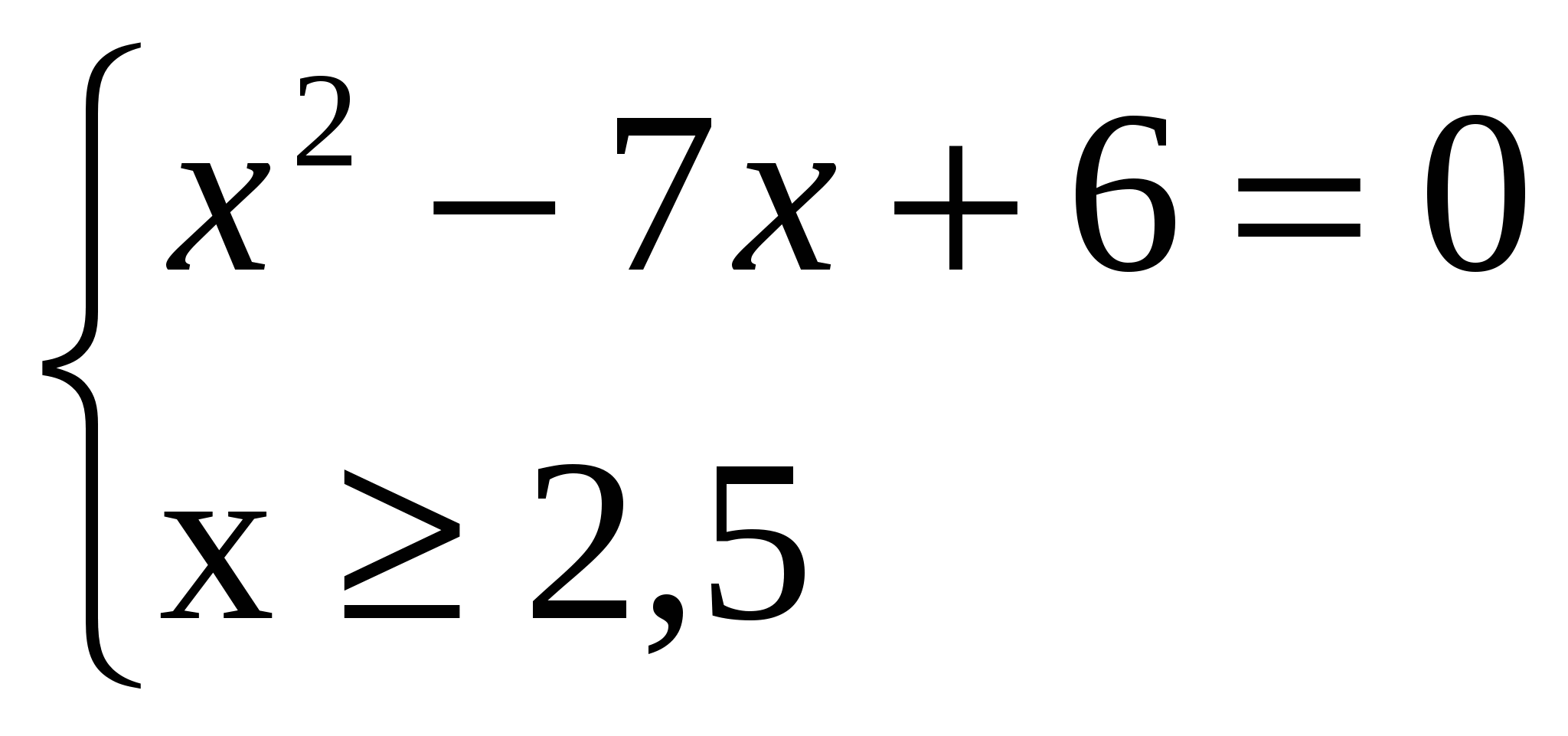 ,
,