Муниципальное бюджетное образовательное учреждение
"Средняя образовательная школа №62" г. Брянска
Рассмотрено Согласовано Утверждено
Руководитель ШМО учителей Председатель ЭМС Директор МБОУ СОШ №62 г. Брянска
математики, физики и информатики _____________ ______________
______________ Протокол №1 Приказ № 193-О от 01.09.2012 г.
28 августа 2012 г. 30 августа 2012 г.
Рабочая программа
по учебному предмету "Математика"
для основного общего образования
8 класс
Срок реализации 1 год
Ф.И.О. составителя Гороховик Елена Александровна
Программа составлена на основе примерной программы основного общего образования по математике, авторской программы Л.С. Атанасяна (Л.С. Атанасян, В.Ф. Бутусов и др. Программы по геометрии 7-9 классы. Москва. Просвещение. 2009 год) и авторской программы А.Г. Мордковича (А.Г. Мордкович, И.И. Зубарева. Программы. Математика 5-6 классы. Алгебра 7-9 классы. Алгебра и начала математического анализа 10-11 классы. Москва. Мнемозина. 2009 год)
2012-2013 учебный годПояснительная записка
Математика 8
5ч в неделю, всего 170 ч.
Рабочая программа по математике 8 класс составлена на основании федерального компонента государственного стандарта основного общего образования, программы по геометрии к учебнику для 7-9 классов общеобразовательных школ авторов Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцева, Э.Г. Позднякова и И.И. Юдиной, программы по алгебре к учебнику для 8 класса общеобразовательных школ автора А.Г.Мордкович.
Данная программа полностью отражает базовый уровень подготовки школьников по разделам программы. Она конкретизирует содержание тем образовательного стандарта и дает примерное распределение часов по разделам курса.
Программа выполняет две основные функции. Информационно-методическая функция позволяет всем участникам процесса получить представление о целях, содержании, общей стратеги обучения, воспитания и развития учащихся средствами данного учебного предмета. Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом их этапов.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как математической модели для описания и исследования разнообразных процессов, для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
Геометрия – один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
На протяжении изучения материала предполагается закрепление и отработка основных умений и навыков, их совершенствование, а также систематизация полученных ранее знание, таким образом, решаются следующие задачи:
● введение терминологии и отработка умения ее грамотно использования;
● развитие навыков изображения планиметрических фигур и простейших геометрических конфигураций;
● совершенствование навыков применения свойств геометрических фигур как опоры при решении задач;
● формирования умения решения задач на вычисление геометрических величин с применением изученных свойств фигур и формул;
● совершенствование навыков решения задач на доказательство;
● отработка навыков решения задач на построение с помощью циркуля и линейки;
● расширение знаний учащихся о треугольниках, четырёхугольниках и окружности.
Цели
Изучение предмета направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Содержание обучения
Алгебра. 3ч в неделю всего 102 ч
Алгебраические дроби (21ч)
Понятие алгебраической дроби. Основное свойство алгебраической дроби. Сокращение алгебраических дробей.
Сложение и вычетание алгебраических дробей.
Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень.
Рациональное выражение. Рациональное уравнение. Решение рациональных уравнений (первые представления).
Степень с отрицательным целым показателем.
Функция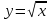 . Свойства квадратного корня (18 ч) . Свойства квадратного корня (18 ч)
Рациональные числа. Понятие квадратного корня из неотрицательного числа. Иррациональные числа. Множество действительных чисел.
Функция у=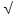 х, её свойства и график. Выпуклость функции. Область значений функции. х, её свойства и график. Выпуклость функции. Область значений функции.
Свойства квадратных корней. Преобразование выражений, содержащих операцию извлечения квадратного корня. Освобождение от иррациональности в знаменателе дроби. Модуль действительного числа. График функции у=|х|. Формула 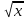 2=|х|. 2=|х|.
Квадратичная функция. Функция у=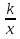 (18ч) (18ч)
Функция у=ах2,её график, свойства.
Функция у=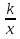 , её свойства, график. Гипербола. Асимптота. , её свойства, график. Гипербола. Асимптота.
Построение графиков функций у= f(х+l), у=f(х)+m,у=f(x+l )+m,у= -f( х ) по известному графику функции у= f( x ).
Квадратный трехчлен. Квадратичная функция, её свойства и график. Понятие ограниченной функции. Построение и чтение графиков кусочных функций, составленных из функций у= С, у= kx+m, у= 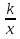 ,у=ax2+bx+c, у= ,у=ax2+bx+c, у=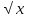 , у=|х|. , у=|х|.
Графическое решение квадратных уравнений.
Квадратные уравнения (21 ч)
Квадратное уравнение. Приведенное (неприведенное0 квадратное уравнение. Полное (неполное) квадратное уравнение. Корень квадратного уравнения. Решение квадратного уравнения методом разложения на множители, методом выделения полного квадрата.
Дискриминант. Формулы корней квадратного уравнения. Параметр. Уравнение с параметром (начальные представления).
Алгоритм решения рационального уравнения. Биквадратное уравнение. Метод введения новой переменной.
Рациональные уравнения как математические модели реальных ситуаций.
Частные случаи формулы корней квадратного уравнения.
Теорема Виета. Разложение квадратного трехчлена на линейные множители.
Иррациональное уравнение.
Неравенства (15 ч)
Свойства числовых неравенств.
Неравенство с переменной. Решение неравенств с переменной. Линейное неравенство. Равносильные неравенства. Равносильное преобразование неравенства.
Квадратное неравенство. Алгоритм решения квадратного неравенства.
Возрастающая функция. Убывающая функция. Исследование функций на монотонность (с использованием свойств числовых неравенств).
Приближенные значения действительных чисел, погрешность приближения, приближение по недостатку и избытку. Стандартный вид числа.
Обобщающее повторение (9 ч)
Геометрия. 2ч в неделю всего 68 ч
Четырехугольники (14ч)
Многоугольник, выпуклый многоугольник, четырехугольник. Параллелограмм, его свойства и признаки. Трапеция. Прямоугольник, ромб, квадрат, их свойства. Осевая и центральная симметрия.
Основная цель – изучить наиболее важные виды четырехугольников – параллелограмм, прямоугольник, ромб, квадрат, трапецию; дать представление о фигурах, обладающих осевой или центральной симметрией.
2.Площадь (14ч)
Понятие площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора.
Основная цель – расширить и углубить полученные в 5-6 классах представления учащихся об измерении и вычислении площадей; вывести формулы площадей прямоугольника, параллелограмма, треугольника, трапеции; доказать одну из главных теорем геометрии – теорему Пифагора.
3. Подобные треугольники (19ч)
Подобные треугольники. Признаки подобных треугольников. Применение подобия к доказательству теорем и решению задач. Синус, косинус и тангенс прямоугольного треугольника.
Основная цель – ввести понятие подобных треугольников; рассмотреть признаки подобия треугольников и их применения; сделать первый шаг в освоении учащимися тригонометрического аппарата геометрии.
4. Окружность (17)
Взаимное расположение прямой и окружности. Касательная к окружности, её свойства и признак. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности.
Основная цель – расширить сведения об окружности, полученные учащимися в 7 классе; изучить новые факты, связанные с окружностью; познакомить учащихся с четырьмя замечательными точками треугольника.
5. Повторение. Решение задач. (10ч)
Требования к уровню подготовки выпускников основной школы
В результате изучения математики ученик должен
знать/понимать
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
Алгебра
уметь
составлять буквенные выражения и формулы по условиям задач;
осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражения;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком, по её аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по её графику; применять графические представления пр решении уравнений, систем, неравентс;
описывать свойства изученных функций, строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимость между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследования построенных моделей аппарата алгебры;
описания зависимости между физическими величинами, соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами.
Геометрия
уметь
пользоваться языком геометрии для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
в простейших случаях строить сечения и развертки пространственных тел;
проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;
вычислять значения геометрических величин (длин, углов, площадей, объемов), в том числе: для углов от 0 до 180 определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, идеи симметрии;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
решать простейшие планиметрические задачи в пространстве;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания реальных ситуаций на языке геометрии;
расчетов, включающих простейшие тригонометрические формулы;
решения геометрических задач с использованием тригонометрии
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Результаты обучения
Результаты обучения представлены в Требованиях к уровню подготовки и задают систему итоговых результатов обучения, которых должны достигать все учащиеся, оканчивающие основную школу, и достижения которых является обязательным условием положительной аттестации ученика за курс основной школы. Эти требования структурированы пр трем компонентам: «знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни». При этом последние два компонента представлены отдельно по каждому из разделов содержания.
Литература
Алгебра:
Мордкович А.Г. «Алгебра – 8». Задачник. 2009г.
Мордкович А.Г. «Алгебра – 8». Учебник. 2009г
Мордкович А.Г. Алгебра 7 – 9. Методическое пособие для учителя.
А.Г.Мордкович. «Беседы с учителем математики».
Александрова Л.А. Алгебра. Контрольные работы// Под. Ред. А.Г. Мордковича.
Александрова Л.А. Алгебра. Самостоятельные работы// Под. Ред. А.Г. Мордковича.
Мордкович А.Г., Тульчинская Е.Е. Алгебра. Тесты. «Алгебра 7 – 9»
Тульчинская Е.Е. Алгебра. Блицопрос. Пособие для учащихся.
Геометрия:
Л.А.Атанасян. «Геометрия 7 – 9» общеобразоват. учрежд.// Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.-М.: Просвещение, 2008г
Л.А.Атанасян. «Изучаем геометрию в 7 – 9 классах»
Геометрия: Рабочая тетрадь для 7 класса, 8 класса, 9 класса. Общеобразовательное. учрежд.// Л.С. Атанасян и др.-М.: Просвещение, 1998г.
Геометрия 7-9 кл. Самостоятельные и контрольные работы к учебнику Л.С. Атанасяна и др:разрезные карточки// Сост. М.А. Иченская.-Волгоград: Учитель, 2007г.
Звавич Л.И. и др. Контрольные и проверочные работы. Геометрия 7-9. Методическое пособие. М.: Дрофа, 2008г.
Литвиненко В.Н. и др. Сборник задач по геометрии (к учебнику Л.С. Атанасяна и др. Геометрия. 7-9 классы). М.: Просвещение, 2006
Поурочное планирование
Математика, 8 класс (по учебникам А.Г. Мордковича, Л.С. Атанасяна) 5 часов в неделю, 170 часов в год
|
№ урока
|
Тема урока
|
ЗУН
|
Домашнее задание
|
Дата
|
|
Повторение, стартовый контроль
|
Восстановить навыки действий с обыкновенными и десятичными дробями, свойства степени, ФСУ
|
|
|
|
Глава 1. Алгебраические дроби
Основные понятия
|
Знать понятие алгебраической дроби и ее допустимых значений; уметь определять область допустимых значений и находить значение буквенного выражения
|
П.1, № 1.1 – 1.12(в,г)
|
|
|
Основное свойство алгебраической дроби
|
Знать основное свойство дроби, уметь сокращать дроби и приводить их к общему знаменателю
|
П.2, № 2.3 – 2.33(г),2.41 -2.45(г)
|
|
|
Сложение и вычитание алгебраических дробей с одинаковыми знаменателями
|
Знать правила сложения и вычитания алгебраических дробей, уметь выполнять сложение и вычитание
|
П.3, №3.1 – 3.21(г)
|
|
|
Сложение и вычитание алгебраических дробей с разными знаменателями
|
Уметь складывать и вычитать дроби с разными знаменателями
|
П.4, № 4.1 – 4.19(г), 4.21 – 4.43(г)
|
|
|
Контрольная работа №1 по теме
«Сложение и вычитание алгебраических дробей»
|
Контроль ЗУН
|
|
|
|
Анализ контрольной работы
Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень
|
Уметь умножать и делить алгебраические дроби, возводить алгебраические дроби в степень
|
П.5, №.5.1 – 5.43(г)
|
|
|
Преобразование рациональных выражений
|
Иметь понятие о рациональных выражениях
Уметь преобразовывать рациональные выражения, упрощать выражения, доказывать тождества
|
П.6, № 6.1 – 6.10(г), 6.11 – 6.18(в,г)
|
|
|
Первые представления о рациональных уравнениях
|
Иметь представление о рациональных уравнениях, знать правила их решения
|
П.7, № 7.1 – 7.21(г), 7.23, 7.26
|
|
|
Степень с отрицательным целым показателем
|
Знать понятие степени с целым отрицательным показателем, уметь выполнять действия со степенью
|
П.8, № 8.1 – 8.21(г)
|
|
|
Контрольная работа № 2 по теме «Умножение и деление алгебраических дробей»
|
Контроль ЗУН
|
|
|
|
Глава V. Четырехугольники
Анализ контрольной работы
Многоугольники
|
Знать понятие многоугольника, его видов
|
П.39 040, вопросы 1-5
№ 364(а,б), 365(а,б,г),368
№366,369,370
|
|
|
Параллелограмм. Свойство параллелограмма
|
Знать определение параллелограмма, свойства; уметь применять свойства при решении задач
|
П.42, вопросы
6 – 8,
№371(а), 372(в),376(в,г)
|
|
|
Признаки параллелограмма
|
Знать и уметь доказывать признаки параллелограмма; применять признаки при решении задач
|
П.43, вопрос9,№ 383,373
№ 375,380,384
|
|
|
Трапеция
|
Знать определение трапеции, виды трапеций, названия элементов
|
П.44, вопросы 10 – 11,№ 386,387,390
№ 391,392,учить док – во теорем
|
|
|
Прямоугольник. Ромб. Квадрат
|
Знать определение фигур; уметь сравнивать и анализировать свойства
|
П.45,
№ 399,401,404
П.46, №405,409,411
|
|
|
Решение задач по теме «Четырехугольники»
|
Уметь решать основные типы задач, применять полученные теоретические знания для решения задач более сложного содержания
|
№394, 398,393(б),415
|
|
|
Контрольная работа №3 по теме «Четырехугольники»
|
Контроль ЗУН
|
|
|
|
Анализ контрольной работы
Глава 2. Функция 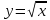 . .
Свойства квадратного корня
Рациональные числа
|
Знать основные понятия из теории чисел,
уметь их различать
|
П.9, № 9.15 – 9.22(в,г)
|
|
|
Понятие квадратного корня из неотрицательного числа
|
Знать понятие квадратного корня из неотрицательного числа, правила вычисления квадратного корня из неотрицательного числа; уметь находить значение квадратного корня
|
П.10, № 10.12 – 10.23(г)
|
|
|
Иррациональные числа
|
Знать основные понятия из теории чисел, уметь их различать и работать с ними
|
П.11, № 11.1 – 11.11(г)
|
|
|
Множество действительных чисел
|
Знать понятие и обозначение множества действительных чисел, основные понятия из теории чисел ,уметь их различать и работать с ними
|
П.12, № 12.4 – 12.16(г)
|
|
|
Функция 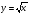 , ее свойства и график , ее свойства и график
|
Знать свойства функции 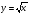 , знать алгоритм построения графика функции, свойства данной функции, иметь понятие о выпуклости функции и области значений функции, уметь строить график , знать алгоритм построения графика функции, свойства данной функции, иметь понятие о выпуклости функции и области значений функции, уметь строить график
|
П.13, №13.1 – 13.18(г)
|
|
|
Свойства квадратных корней
|
Знать свойства квадратных корней и применять их при решении заданий, содержащих операцию извлечения квадратного корня
|
П.14, № 14.1 – 14.26(г)
|
|
|
Преобразование выражений, содержащих операцию извлечения квадратного корня
|
Уметь пользоваться свойствами квадратных корней при преобразовании выражений, содержащих радикал
|
П.15, № 15.1 -15.81(г)
|
|
|
Контрольная работа № 4 по теме «Квадратный корень»
|
Контроль ЗУН
|
|
|
|
Глава VI. Площадь
Площадь многоугольника
|
Знать понятие площади, свойства площади
|
П.48 - 40, вопросы1 – 2,
№ 448,449(б), 450(б), 446
№ 454,455,456, П.50, вопрос3
|
|
|
Площадь параллелограмма
|
Знать формулу для вычисления площади параллелограмма; решать задачи на применение формул
|
П.51, № 459,460,464(а), 462, вопрос4
|
|
|
Площадь треугольника
|
Знать формулу для вычисления площади треугольника; решать задачи на применение формул
|
П.52,
вопрос5 – 6,
№ 468(в), 473,469
№ 479(в), 476,477(а)
|
|
|
Площадь трапеции
|
Знать формулу для вычисления площади трапеции; решать задачи на применение формул
|
П.53, вопрос7,
№ 480(б,в), 481,478
№ 466,467,тест
|
|
|
Теорема Пифагора
|
Знать и уметь доказывать теорему Пифагора; уметь применять ее при решении треугольников
|
П.54, вопрос8,
№ 483,484,486(в,г)
П.55,вопросы
9-10
№ 498,499(б),488
|
|
|
Решение задач по теме «Площади»
|
Совершенствование навыков решения задач
|
№ 489(а,в),491(а),
493
№ 494,495(б),524
|
|
|
Контрольная работа №5 по теме «Площади»
|
Контроль ЗУН
|
|
|
|
Анализ контрольной работы
Модуль действительного числа
|
Знать определение модуля действительного числа, его свойства и геометрический смысл, уметь строить график функции 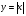 и пользоваться формулой и пользоваться формулой  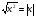
|
П.16,№ 16,6 – 16.8(г), 16.16,16.19, 16.21 – 16.31(г)
|
|
|
|
|
|
|
|
Глава 3. Квадратичная функция. Функция 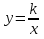 Функция Функция 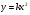 , ее свойства и график , ее свойства и график
|
Знать свойства функции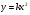 , уметь стоить график и по графику определять свойства , уметь стоить график и по графику определять свойства
|
П.17, № 17.1 – 17.46(г), 17.53
|
|
|
Функция 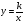 , ее свойства и график , ее свойства и график
|
Знать, что графиком обратной пропорциональности является гипербола, свойства функции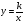 , уметь строить график и по графику определять свойства функции , уметь строить график и по графику определять свойства функции
Иметь представление об асимптотах графика функции
|
П.18, №18.5, 18.8, 18.14 – 18.19(г),18.25
|
|
|
Контрольная работа №6 по теме «Функция»
|
|
|
|
|
Анализ контрольной работы
Как построить график функции 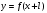 , если известен график функции , если известен график функции 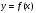
|
Знать правило построения графика такого вида, уметь выполнять преобразование графика
|
П.19, № 19.1 – 19.10(г)19.16,
19.25
|
|
|
Как построить график функции 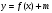 , если известен график функции , если известен график функции 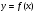
|
Знать правило построения графика такого вида, уметь выполнять преобразование графика
|
П.20, №20.1 – 20.4(г), 20.8, 20.10,20.26,
20.31
|
|
|
Как построить график функции 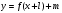 , если известен график функции , если известен график функции 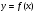
|
Знать правило построения графика такого вида, уметь выполнять преобразование графика. Уметь строить график функции вида 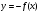 ,если задана функция ,если задана функция 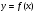
|
П.21, № 21.1 – 21.10(г), 21.19
|
|
|
Функция 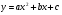 , ее свойства и график , ее свойства и график
|
Знать : понятие о квадратном трехчлене, квадратичной функции общего вида 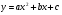 ,ее свойства и название графика( парабола) , алгоритм построения графика функции ,ее свойства и название графика( парабола) , алгоритм построения графика функции
Уметь находить координаты вершины параболы и ось симметрии, строить график квадратичной функции. Иметь понятие об ограниченности функции
Уметь строить и читать графики кусочно-заданных функций, полученных из функций 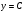 , , 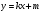 , ,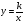 , , 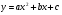 , , 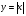 , , 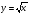
|
П.22, 3 22.7 – 22.12(г), 22.19, 22.20 – 22.23(г)
|
|
|
Графическое решение квадратных уравнений
|
Уметь решать квадратные уравнения графическим способом
|
П.23, № 23.1 – 23.8(г)
|
|
|
Контрольная работа №7 по теме «Квадратичная функция»
|
Контроль ЗУН
|
|
|
|
Глава VII. Подобные треугольники
Определение подобных треугольников
|
Знать понятие пропорциональности сторон, подобия, подобных треугольников; уметь составлять соотношения сходственных сторон
|
П.56 – 57, вопросы
1 – 3,
№534,536(а) 538,542
№ П.58, вопрос4,
№544,543,546,
549
|
|
|
Первый признак подобия
|
Знать и уметь доказывать признак; распознавать подобие треугольников по набору элементов; уметь решать задачи
|
П.59, № 552,557(в),558
|
|
|
Второй признак подобия
|
Знать и уметь доказывать признак; распознавать подобие треугольников по набору элементов; уметь решать задачи
|
П.60, №559,560,561
|
|
|
Третий признак подобия
|
Знать и уметь доказывать признак; распознавать подобие треугольников по набору элементов; уметь решать задачи
|
П.61, № 562,563,604,605
|
|
|
Контрольная работа №8 по теме «Признаки подобия треугольников»
|
Контроль ЗУН
|
|
|
|
Анализ контрольной работы
Применение подобия к доказательству теорем и решению задач
|
Знать определение средней линии трапеции, ее свойства; уметь решать задачи по теме. Знать свойства пропорциональных отрезков, применять их при решении задач. Уметь решать задачи на построение
|
П.62, вопросы
8 – 9
№ 556,570,571
№ 568,569
|
|
|
Соотношения между сторонами и углами в прямоугольном треугольнике
|
Знать определение синуса, косинуса и тангенса, знать их значения для некоторых углов; уметь решать задачи по теме
|
П.63, вопросы 10 – 11,
№ 572,573,574
№ 575,577,579
П.66, вопросы 15 – 17
№ 591,592,593,
П.67,вопрос18,
№ 595,597,598
|
|
|
Контрольная работа №9 по теме «Применение подобия»
|
Контроль ЗУН
|
|
|
|
Анализ контрольной работы
Глава 4. Квадратные уравнения
Основные понятия
|
Знать определение квадратного уравнения, его корней, вилы: приведенное и неприведенное, полное и неполное
Уметь решать квадратные уравнения методом разложения на множители и выделением полного квадрата
|
П.24, № 24.16 – 24.24(г)
|
|
|
Формулы корней квадратных уравнений
|
Знать6 понятие дискриминанта и формулу для его вычисления, формулу корней квадратного уравнения, уметь применять ее при решении уравнений. Иметь начальные представление о параметре и решении уравнений, содержащих параметр
|
П.25, № 25.1 – 25.20(г), 25.24,
25.28,25.32
|
|
|
Рациональные уравнения
|
Знать понятие рационального уравнения, ОДЗ уравнения, уметь решать рациональные уравнения по алгоритму Знать понятие биквадратного уравнения и уметь решать их методом введения новой переменной
|
П.26, № 26.1- 26.11(г), 26.17 – 26.19(г)
|
|
|
Контрольная работа № 10 по теме «Квадратное уравнение»
|
Контроль ЗУН
|
|
|
|
Рациональные уравнения как математические модели реальных ситуаций
|
Знать и уметь применять три этапа математического моделирования для решения текстовых задач с помощью рациональных уравнений
|
П.27, № 27.2, 27.4, 27.8, 27.12,27.18,
27.27, 27.32
|
|
|
Еще одна формула корней квадратного уравнения
|
Знать частные случаи формулы корней квадратного уравнения
Уметь решать квадратные уравнения с помощью различных формул
|
П.28, № 28.1 – 28.6(г), 28.8, 28.10, 28.14,28.19 –
28.21(г)
|
|
|
Теорема Виета
|
Знать и уметь доказывать теорему Виета, уметь применять ее при решении квадратных и рациональных уравнений. Уметь раскладывать квадратный трехчлен на линейные множители
|
П.29¸№ 29.2 – 29.21(г),
29.23 – 29.25(б)
|
|
|
Контрольная работа № 7 «Дробно-рациональные уравнения»
|
Контроль ЗУН
|
|
|
|
Анализ контрольной работы
Иррациональные уравнения
|
Знать понятие иррационального уравнения, уметь решать основные виды уравнений методом возведения в квадрат
|
П.30, № 30.1 – 30.13(в,г)
|
|
|
Глава VIII. Окружность
Касательная к окружности
|
Знать три вида взаимного расположения и их условия. Знать виды взаимного расположения окружности и их условия . Знать определение касательной, ее свойства, уметь строить касательную к окружности, уметь решать задачи
|
П.68, вопросы 1- 2,
№631,632,633
П.69,вопросы3 – 7
№ 634,636,639
№ 641,643,645,648
|
|
|
Центральные и вписанные углы
|
Знать определение дуги, уметь находить градусную меру дуги, решать задачи. Знать определения центрального и вписанного углов, уметь доказывать теорему, знать соотношение между центральными и вписанными углами, уметь решать задачи
|
П.70,
вопросы8 – 10
№ 649,650,652
П.71, вопросы11 – 13
№ 654,655,657,659
П.71, вопрос 14
№ 666,671,668
№ 672,673
|
|
|
Четыре замечательные точки треугольника
|
Знать свойства биссектрис, высот, медиан, и серединных перпендикуляров треугольника
|
П.72, вопросы15 – 16,
№ 675,676,678
П.72,
Вопросы17 – 19
№ 679,680,681
|
|
|
Вписанная окружность
|
Знать определение вписанной окружности, уметь строить вписанную окружность
|
П74, вопросы 21 – 22
№ 689,692,694
|
|
|
Описанная окружность
|
Знать определение описанной окружности, уметь строить описанную окружность
|
П.75, вопросы 24 – 25,
702,705,707,711
|
|
|
Решение задач
|
Уметь решать задачи по теме
|
№ 709,710,731,735,
№ 726,728
|
|
|
Контрольная работа №5 по теме «Окружность»
|
Контроль ЗУН
|
|
|
|
Анализ контрольной работы
Глава 5. Неравенства
Свойства числовых неравенств
|
Иметь представление о числовых неравенствах и неравенствах с переменной, равносильности неравенств и их равносильном преобразовании
Знать свойства неравенств; уметь сравнивать числа и выражения, применяя свойства неравенств
|
П.31, № 31.1 – 31.9(г)
|
|
|
Исследование функций на монотонность
|
Знать понятие возрастающей и убывающей функций, уметь исследовать функцию на монотонность с использованием свойств числовых неравенств
|
|
|
|
Решение линейных неравенств
|
Знать алгоритм решения линейных неравенств, уметь решать неравенства
|
П.33, №33.4 – 33.9(г), 33.10,33.14 – 33.24(г0
|
|
|
Решение квадратных неравенств
|
Уметь решать квадратные неравенства по алгоритму
|
П.34, №34.1 – 34.27(г)
|
|
|
Контрольная работа № 8 по теме «Неравенства»
|
Контроль ЗУН
|
|
|
|
Анализ контрольной работы
Приближенные значения действительных чисел
|
Уметь находить приближенное значение действительного числа, знать понятие погрешности приближения, погрешность по избытку и недостатку
|
П.35,№ 35.1 – 35.9(г)
|
|
|
Стандартный вид положительного числа
|
Уметь представлять число в стандартном виде
|
П.36.№ 36.1 – 36.13(г)
|
|
|
Повторение
|
|
|
 Скачать 290.1 Kb.
Скачать 290.1 Kb.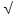 х, её свойства и график. Выпуклость функции. Область значений функции.
х, её свойства и график. Выпуклость функции. Область значений функции. 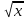 2=|х|.
2=|х|.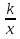 , её свойства, график. Гипербола. Асимптота.
, её свойства, график. Гипербола. Асимптота. 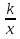 ,у=ax2+bx+c, у=
,у=ax2+bx+c, у=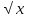 , у=|х|.
, у=|х|.
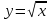 . Свойства квадратного корня (18 ч)
. Свойства квадратного корня (18 ч)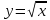 .
. 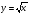 , ее свойства и график
, ее свойства и график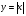 и пользоваться формулой
и пользоваться формулой 
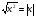
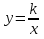 Функция
Функция 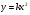 , ее свойства и график
, ее свойства и график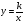 , ее свойства и график
, ее свойства и график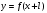 , если известен график функции
, если известен график функции 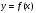
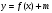 , если известен график функции
, если известен график функции 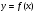
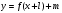 , если известен график функции
, если известен график функции 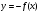 ,если задана функция
,если задана функция 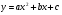 , ее свойства и график
, ее свойства и график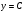 ,
, 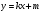 ,
,