|
Рабочая программа по математике для 5 9 классов (базовый уровень) Автор составитель рабочей программы учитель математики
    Муниципальное бюджетное общеобразовательное учреждение Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа №54»
Рабочая программа
по математике для 5 - 9 классов (базовый уровень)
Автор – составитель
рабочей программы
учитель математики
Е.Г. Бачурина
Обсуждено на заседании
методического объединения
Протокол №4
от 26 марта 2013 г.
Руководитель
О.В.Зубанова______________
Утверждено на педагогическом совете
Протокол №4
от 28 марта 2013 г.
Директор МБОУ «СОШ №54»
Н.Г. Зырянова_________________
Кемерово
2013
Содержание
1. Пояснительная записка …………………………………………... 3
|
|
2. Содержание программы.………………………………………….. 10
3. Учебно-тематическое планирование в 5 классе………………… 17
4. Учебно-тематическое планирование в 6 классе…………………20
5. Учебно-тематическое планирование в 7 классе…………………22
6. Учебно-тематическое планирование в 8 классе….……………..26
7. Учебно-тематическое планирование в 9 классе….……………..31
8. Список литературы для учителя…………………………………..34
|
|
9. Список литературы для учащихся…...…...……………………….37
|
|
10. Перечень ключевых слов…………………………………………39
11. Контрольные материалы………………………………………….42
.
|
|
Пояснительная записка
Без базовой математической подготовки невозможно достичь высокого уровня образования. Школьное образование в современных условиях призвано научить детей самостоятельно добывать информацию и уметь ею пользоваться. Это предполагает направленность целей обучения на формирование личности, способной к жизнедеятельности и самоопределению в информационном обществе, ясно представляющей свои потенциальные возможности, ресурсы и способы реализации выбранного жизненного пути.
Главной целью школьного образования в современных условиях является развитие ребёнка как компетентной личности путём включения его в различные виды ценностной человеческой деятельности: учёба, познание, коммуникация, профессионально – трудовой выбор, личностное саморазвитие, ценностные ориентации, поиск смыслов жизнедеятельности.
Особенность изучаемого курса математики состоит в формировании математического стиля мышления, проявляющегося в определённых умственных навыках. Использование в математике нескольких математических языков даёт возможность развивать у учащихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые средства.
Рабочая программа по математике составлена на основе Федерального компонента государственного стандарта основного общего образования.
Данная программа ориентирована на обучающихся 5 – 9 классов и реализуется на основе следующих документов:
Федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования (приказ МО РФ от 5 марта 2004 года №1089)
Федерального базисного учебного плана для начального общего, основного общего и среднего (полного) общего образования (приказ МО РФ от 9 марта 2004 года №1312)
Примерные программы по математике. (Сборник нормативных документов. Математика / составили Э. Д. Днепров, А. Г. Аркадьев. М.: Дрофа, 2008)
Программа. Планирование учебного материала. Математика.5-6 классы./ автор-составитель В.И.Жохов - М.: Мнемозина, 2010.
Программы. Математика. 5 – 6 классы. Алгебра. 7 – 9 классы. Алгебра и начала анализа. 10 – 11 классы / авт.-сост. И. И. Зубарева, А. Г. Мордкович. – М.: Мнемозина, 2009
Программы общеобразовательных учреждений. Геометрия. 7-9 классы / сост. Т.А Бурмистрова. – М.: Просвещение, 2009.
Изучение математики в 5 – 9 классах направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Требования Государственного образовательного стандарта 2004 года определяют задачи обучения:
приобретение математических знаний и умений;
овладение обобщенными способами мыслительной, творческой деятельности;
освоение компетенций: учебно–познавательной, коммуникативной, рефлексивной, личностного развития, ценностно – ориентированной и профессионально – трудового выбора.
В результате изучения математики на ступени основного общего образования ученик должен
знать/понимать1:
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; приводить примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.
Арифметика
уметь:
правильно употреблять термины, связанные с различными видами чисел и способами их записи: целое, дробное, десятичная дробь, переход от одной формы записи к другой (например, проценты в виде десятичной дроби; выделение целой части из неправильной дроби); решать основные задачи на дроби;
сравнивать числа, упорядочивать наборы чисел, понимать связь отношений «больше», «меньше» с расположением точек на координатной прямой;
выполнять арифметические действия с рациональными числами; сочетать при вычислении устные и письменные приемы;
составлять и решать пропорции;
производить прикидку результата вычислений;
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические действия с обыкновенными дробями с однозначным знаменателем и числителем;
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты – в виде дроби и дробь – в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;
округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
решать текстовые задачи, включая задачи, связанные с отношением и пропорциональностью величин, дробями и процентами;
использовать приобретенные знания и умения в практической
деятельности и повседневной жизни для:
Алгебра
уметь:
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики.
использовать приобретенные знания и умения в практической
деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами;
Элементы логики, комбинаторики, статистики
и теории вероятностей
уметь:
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность суждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов, а также с использованием правила умножения;
вычислять средние значения результатов измерения;
находить частоту события, используя собственные наблюдения и готовые статистические данные;
находить вероятности случайных событий в простейших случаях;
использовать приобретенные знания и умения в практической
деятельности и повседневной жизни для:
выстраивания аргументации при доказательстве (в форме монолога и диалога);
распознавания логически некорректных суждений;
записи математических утверждений, доказательств;
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
решения учебных и практических задач, требующих систематического перебора вариантов;
сравнения шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;
понимания статистических утверждений.
Геометрия
уметь:
распознавать на чертежах и моделях геометрические фигуры (отрезки, углы, треугольники, многоугольники, окружность, круг); изображать указанные геометрические фигуры; выполнять чертежи по условию задачи;
владеть практическими навыками использования геометрических инструментов для изображения фигур, а так же для нахождения длин отрезков и величин углов
решать задачи на вычисление геометрических величин (длин, углов, площадей, объемов), применяя изученные свойства фигур и формулы.
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
в простейших случаях строить сечения и развертки пространственных тел;
проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;
вычислять значения геометрических величин (длин, углов, площадей, объемов), в том числе: для углов от 0 до 180 определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
решать простейшие планиметрические задачи в пространстве;
использовать приобретенные знания и умения в практической
деятельности и повседневной жизни для:
описания реальных ситуаций на языке геометрии;
расчетов, включающих простейшие тригонометрические формулы;
решения геометрических задач с использованием тригонометрии;
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
В 5– 9 классах курс математики делится на три раздела: математика – 340 часов, алгебра – 306 часов, геометрия – 204 часов. Общее количество часов, отводимое на изучение математики, – 850.
Распределение учебного материала по темам:
Математика 5 класс
Натуральные числа и шкалы.
Сложение и вычитание натуральных чисел.
Умножение и деление натуральных чисел.
Площади и объемы.
Обыкновенные дроби.
Десятичные дроби. Сложение и вычитание десятичных дробей.
Умножение и деление десятичных дробей.
Инструменты для вычислений и измерений.
Математика 6 класс
Делимость чисел.
Сложение и вычитание дробей с разными знаменателями.
Умножение и деление обыкновенных дробей.
Отношение и пропорция.
Положительные и отрицательные числа.
Сложение и вычитание положительных и отрицательных чисел.
Умножение и деление положительных и отрицательных чисел.
Решение уравнений.
Координаты на плоскости.
Алгебра
7 класс
Математический язык. Математическая модель.
Линейная функция.
Системы двух линейных уравнений с двумя переменными.
Степень с натуральным показателем и ее свойства.
Одночлены. Операции над одночленами.
Многочлены. Арифметические операции над многочленами.
Разложение многочлена на множители.
Функция 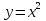 . .
8 класс
Алгебраические дроби.
Функция 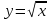 . Свойства квадратного корня. . Свойства квадратного корня.
Квадратичная функция. Функция 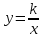 . .
Квадратные уравнения.
Неравенства.
9 класс
Рациональные неравенства и их системы.
Системы уравнений.
Числовые функции.
Прогрессии.
Элементы комбинаторики, статистики и теории вероятностей.
Геометрия
7 класс
Начальные геометрические сведения.
Треугольники.
Параллельные прямые.
Соотношения между сторонами и углами треугольника.
8 класс
Четырехугольники.
Площадь.
Подобные треугольники.
Окружность.
9 класс
Векторы. Метод координат.
Соотношения между сторонами и углами треугольника.
Скалярное произведение векторов.
Длина окружности и площадь круга.
Движения
Начальные сведения из стереометрии.
Об аксиомах планиметрии.
Промежуточная аттестация проводится в форме самостоятельных письменных работ, математических диктантов, тестов. Итоговая аттестация – согласно нормативным документам МО РФ
Формы контроля.
Текущий контроль: практические работы, самостоятельные работы, математические диктанты, самостоятельные работы по теории, письменные ответы по карточкам, устный опрос у доски, фронтальный опрос у доски, взаимный контроль, самоконтроль.
Тематический контроль: тесты, контрольные работы, зачеты, творческие работы, практические работы.
Итоговый контроль: итоговые контрольные работы.
Тематическое планирование составлено к учебнику математики Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. Математика. 5 класс. - М.: Мнемозина, 2010 г., к учебнику математики Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. Математика. 6 класс. - М.: Мнемозина, 2005 г., к учебно - методическому комплексу А. Г. Мордковича и др. Алгебра. 9 класс. – М.: Мнемозина, 2008 – 2011, к учебно - методическому комплексу Л. С. Атанасян и др. Геометрия. 7 – 9 класс. – М.:Просвещение, 2008 – 2011.
Содержание программы
5 КЛАСС
Натуральные числа и шкалы (15 ч)
Обозначение натуральных чисел. Отрезок. Длина отрезка. Треугольник. Плоскость. Прямая. Луч. Шкалы и координаты. Меньше или больше.
Сложение и вычитание натуральных чисел (21 ч)
Сложение натуральных чисел и его свойства. Вычитание. Числовые и буквенные выражения. Буквенная запись свойств сложения и вычитания. Уравнения.
Умножение и деление натуральных чисел (27 ч)
Умножение натуральных чисел и его свойства. Деление. Деление с остатком. Упрощение выражений. Порядок выполнения действий. Квадрат и куб.
Площади и объемы (12 ч)
Формулы. Площадь. Формула площади прямоугольника. Единицы измерения площадей. Прямоугольный параллелепипед. Объемы. Объем прямоугольного параллелепипеда.
Обыкновенные дроби (23 ч)
Окружность и круг. Доли. Обыкновенные дроби. Сравнение дробей. Правильные и неправильные дроби. Сложение и вычитание дробей с одинаковыми знаменателями. Деление и дроби. Смешанные числа. Сложение и вычитание смешанных чисел.
Десятичные дроби. Сложение и вычитание десятичных дробей (13ч)
Десятичная запись дробных чисел. Сравнение десятичных дробей. Сложение и вычитание десятичных дробей. Приближенные значения чисел. Округление чисел.
Умножение и деление десятичных дробей (26 ч)
Умножение десятичных дробей на натуральные числа. Деление десятичных дробей на натуральные числа. Умножение десятичных дробей. Деление десятичных дробей. Среднее арифметическое.
|
|
|
 Скачать 0.65 Mb.
Скачать 0.65 Mb.


 Муниципальное бюджетное общеобразовательное учреждение
Муниципальное бюджетное общеобразовательное учреждение  .
.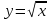 . Свойства квадратного корня.
. Свойства квадратного корня.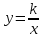 .
.