Протокол №1 от «31» августа 2010г. Руководитель омо: Калашникова И. Р

Название	Протокол №1 от «31» августа 2010г. Руководитель омо: Калашникова И. Р
страница	2/2
Дата	27.02.2016
Размер	397.63 Kb.
Тип	Протокол

1 2

Критерии и нормы оценки знаний, умений и навыков обучающихся по математике

1. Оценка письменных контрольных работ обучающихся по математике.

Ответ оценивается отметкой «5», если:

- работа выполнена полностью;

- в логических рассуждениях и обосновании решения нет пробелов и ошибок;

- в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

- работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

- допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

- допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

- допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Отметка «1» ставится, если:

- работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

2.Оценка устных ответов обучающихся по математике

Ответ оценивается отметкой «5», если ученик:

- полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

- изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

- правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

- показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

- продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;

- отвечал самостоятельно, без наводящих вопросов учителя;

- возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

- в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

- допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;

- допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

- неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);

- имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

- ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

- при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

- не раскрыто основное содержание учебного материала;

- обнаружено незнание учеником большей или наиболее важной части учебного материала;

- допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Отметка «1» ставится, если:

- ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.

Общая классификация ошибок.

При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

3.1. Грубыми считаются ошибки:

незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.

3.2. К негрубым ошибкам следует отнести:

неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.

3.3. Недочетами являются:

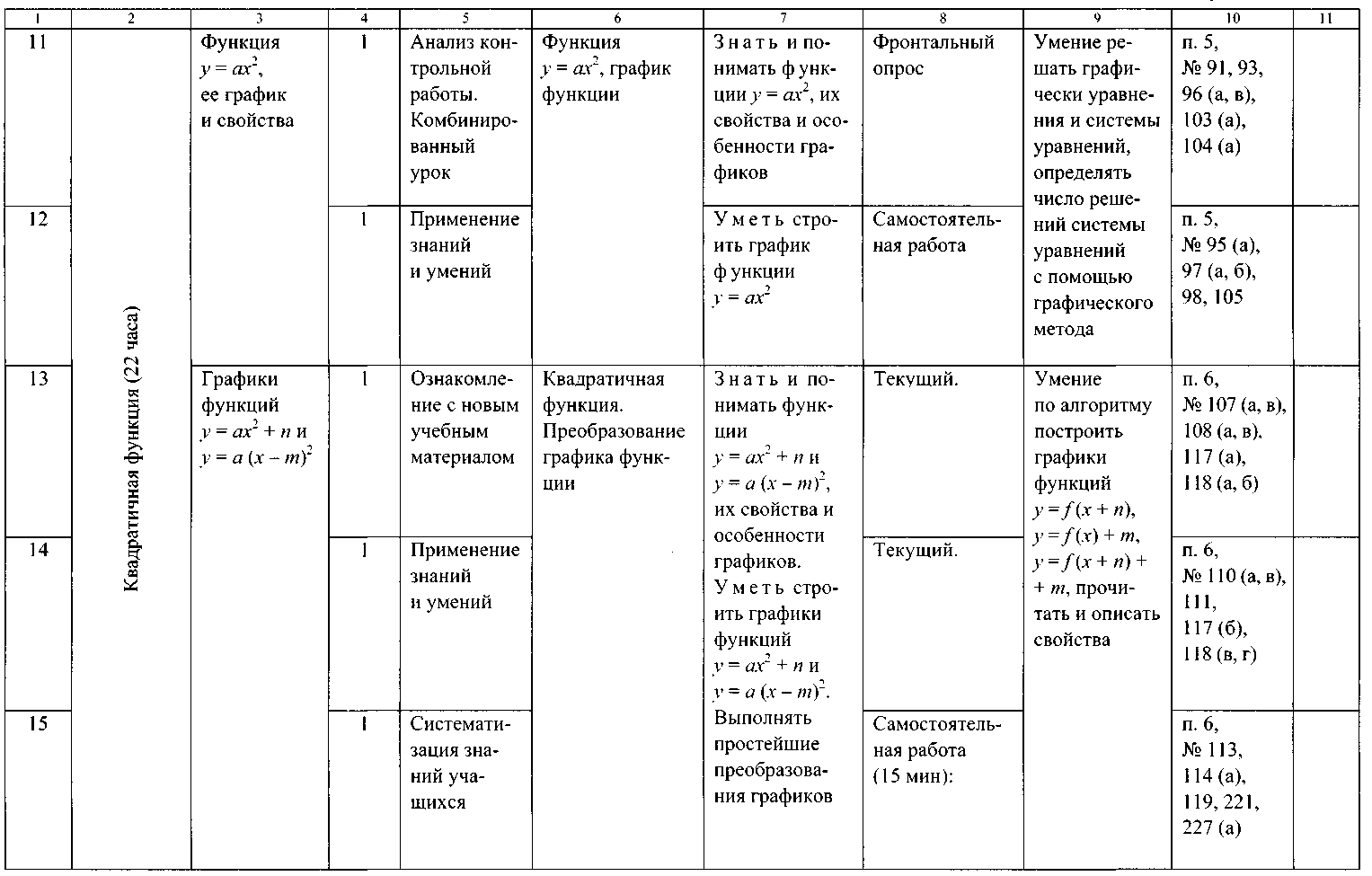
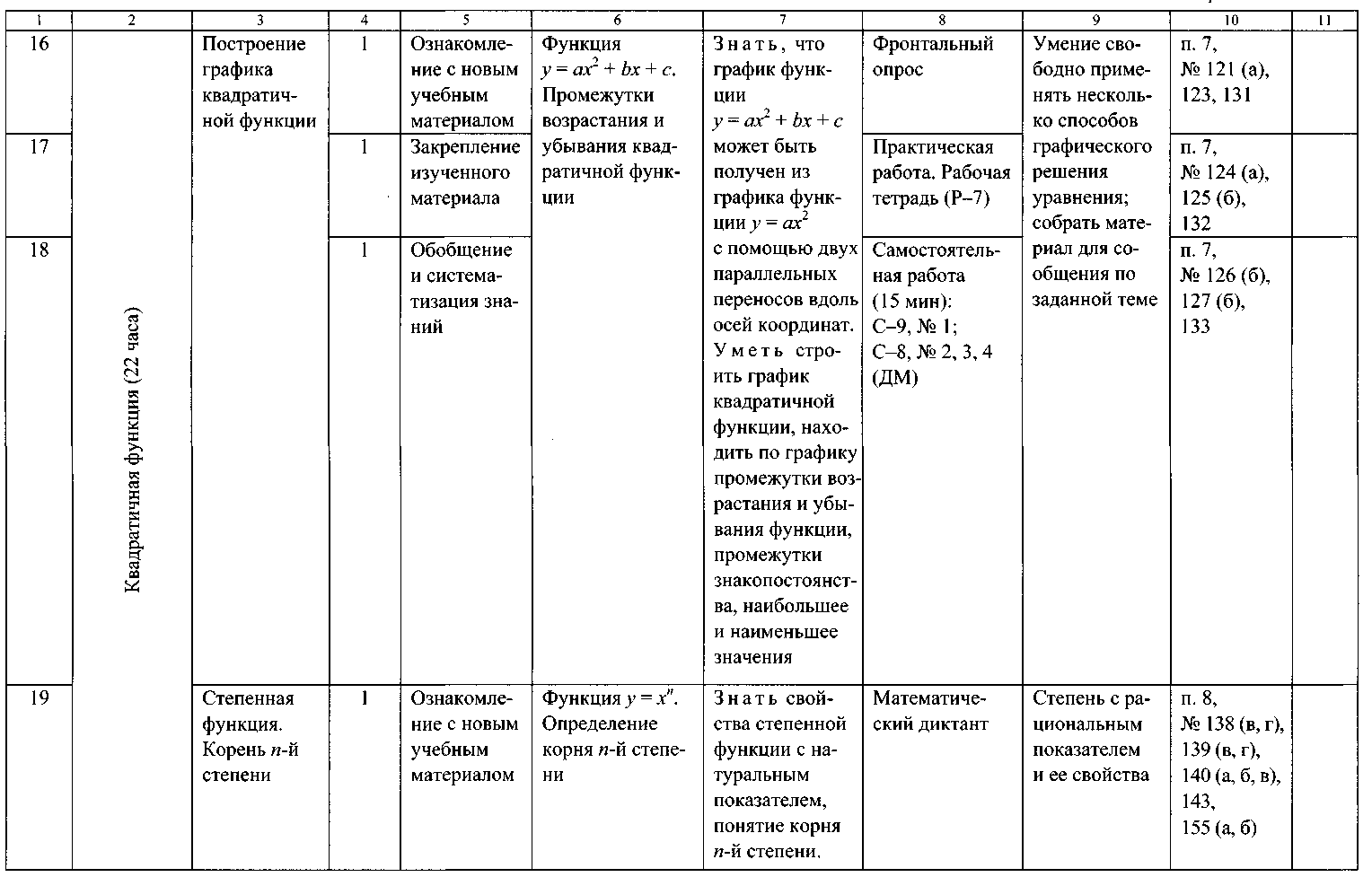
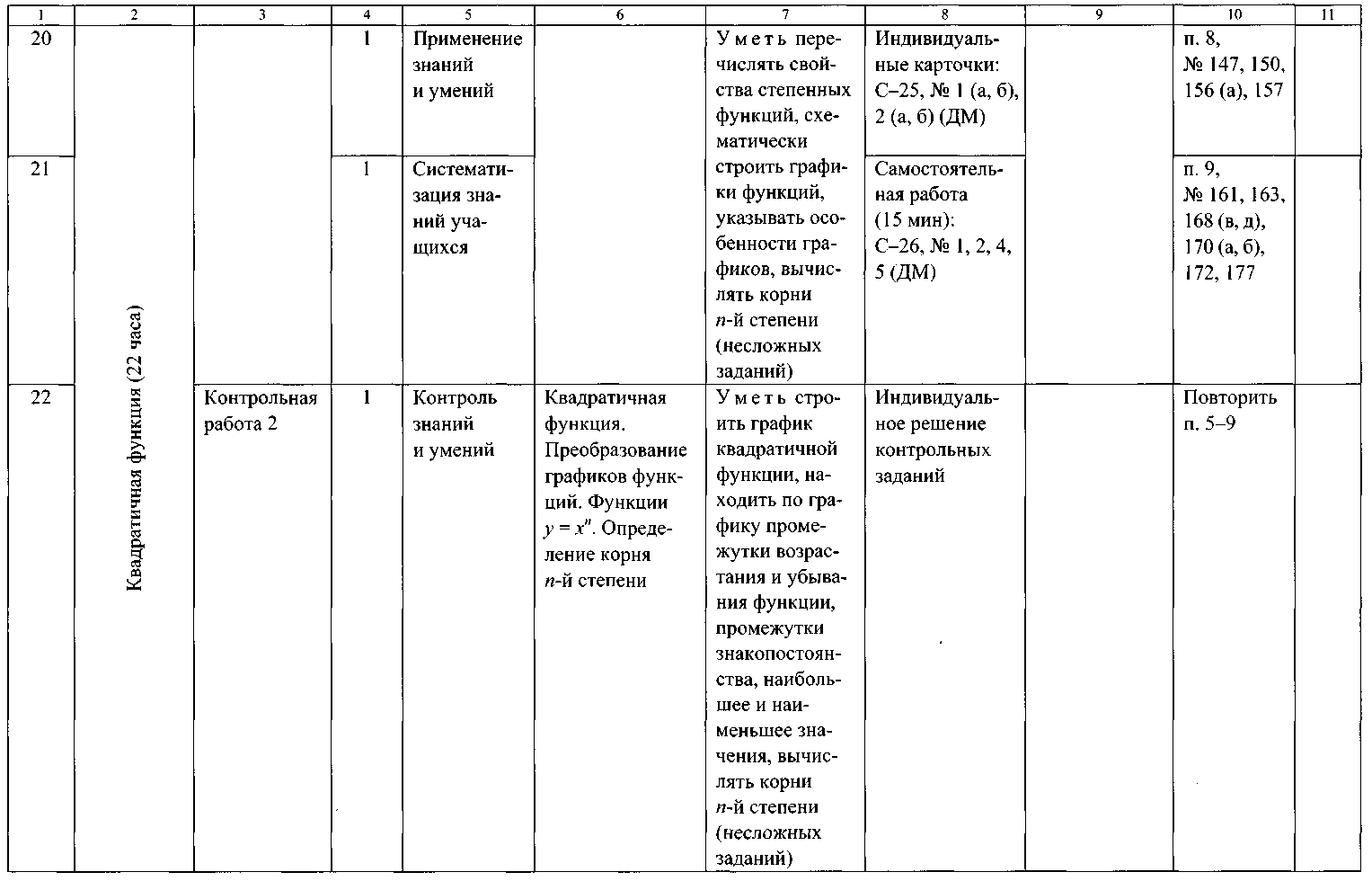
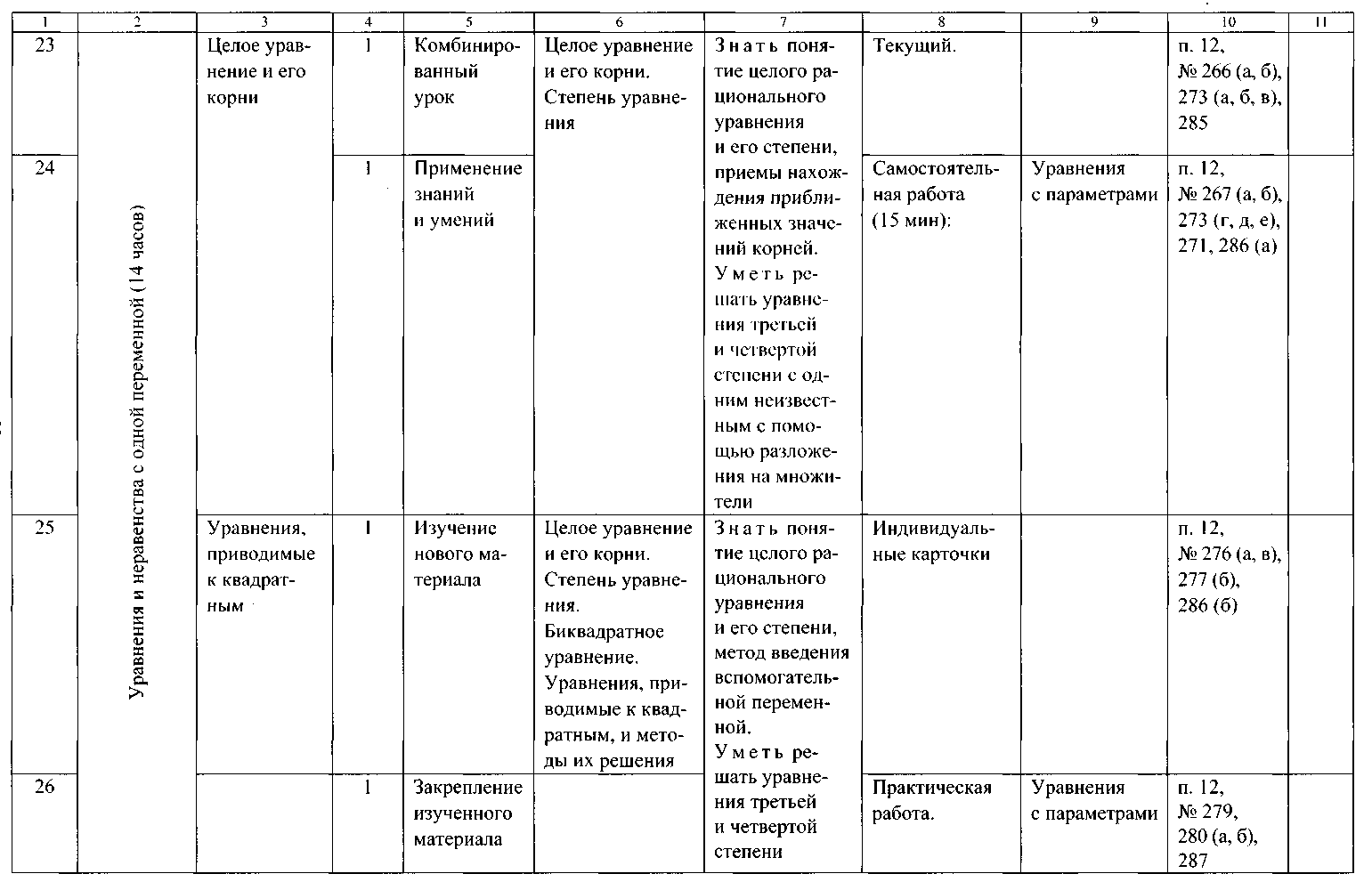
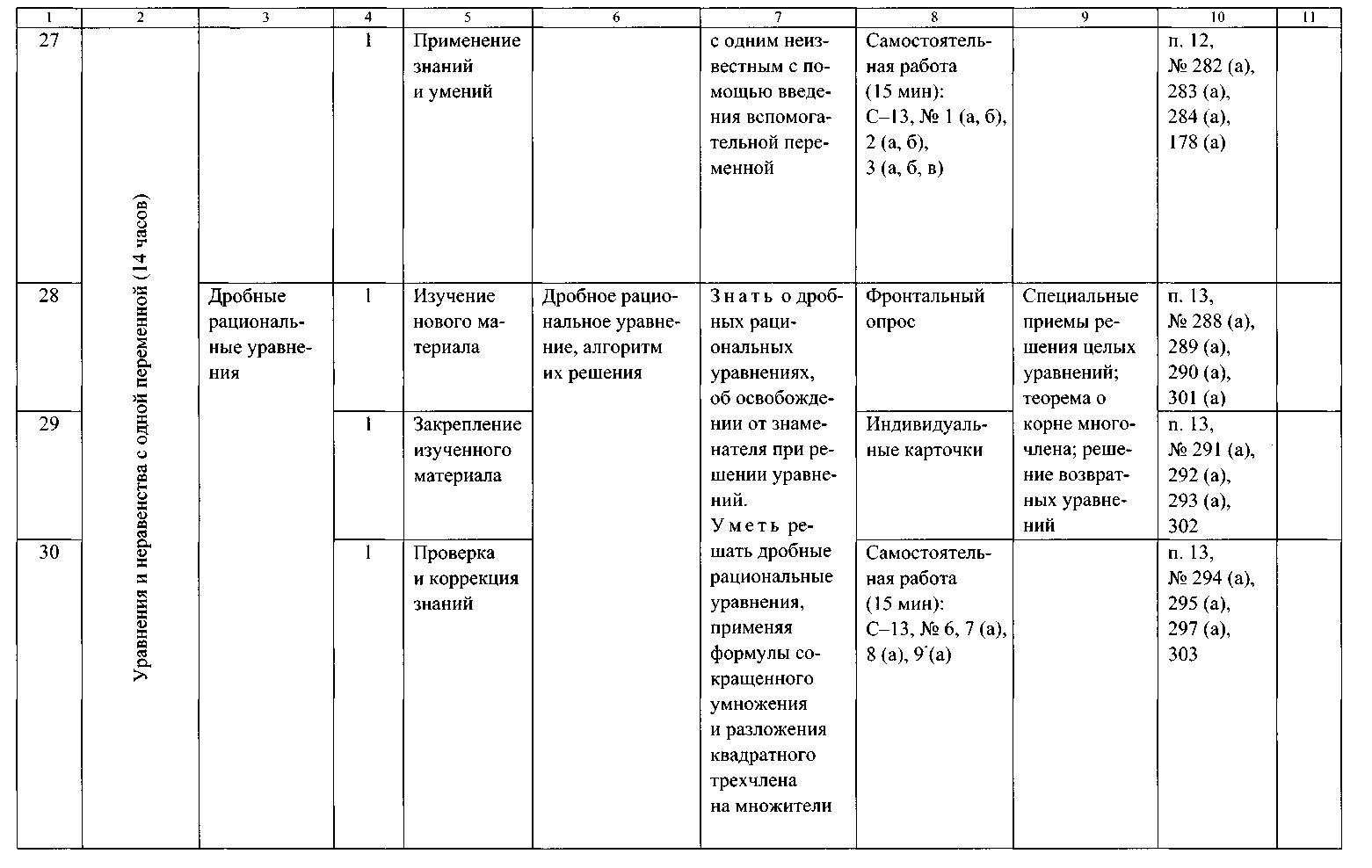
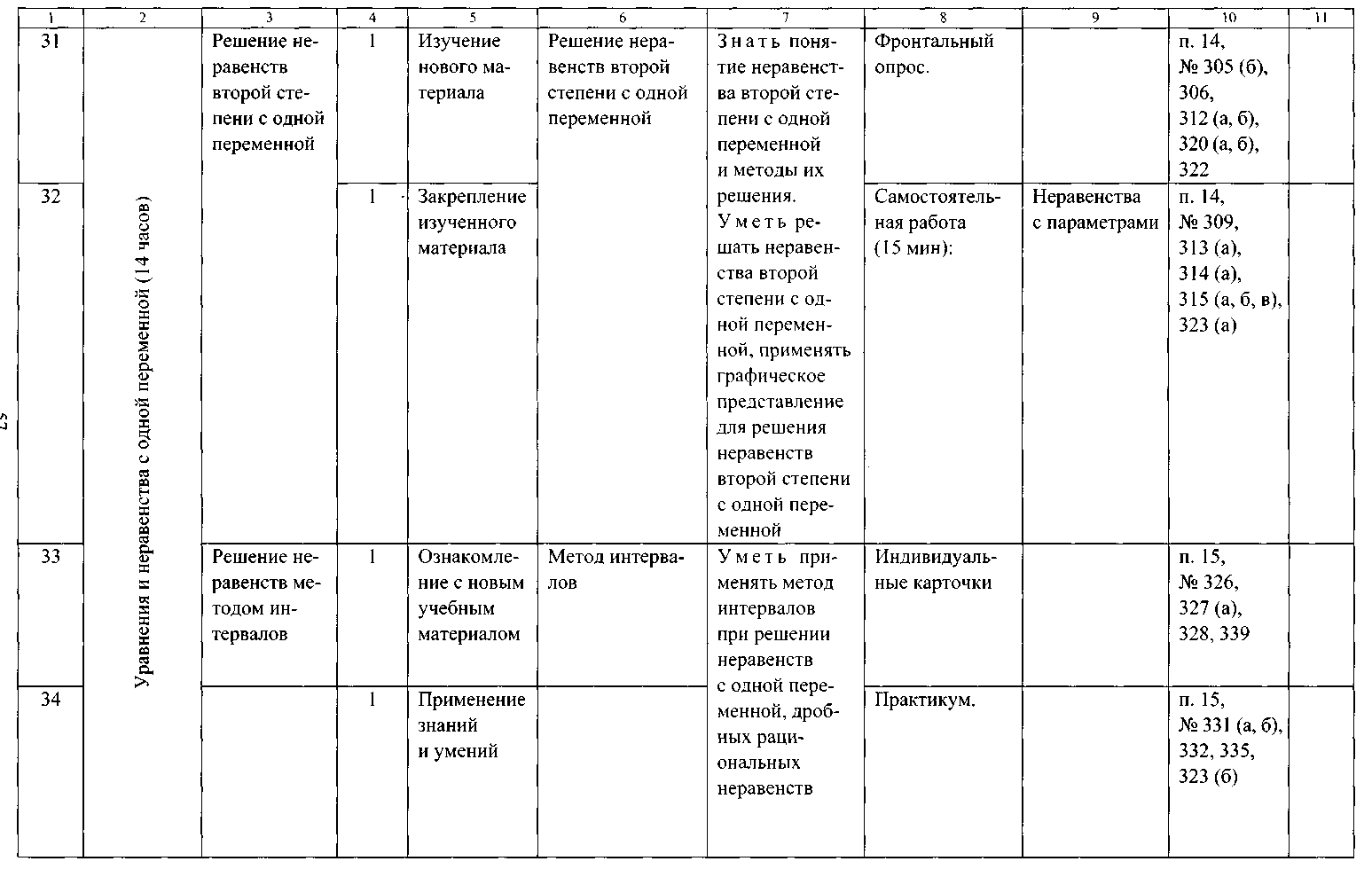
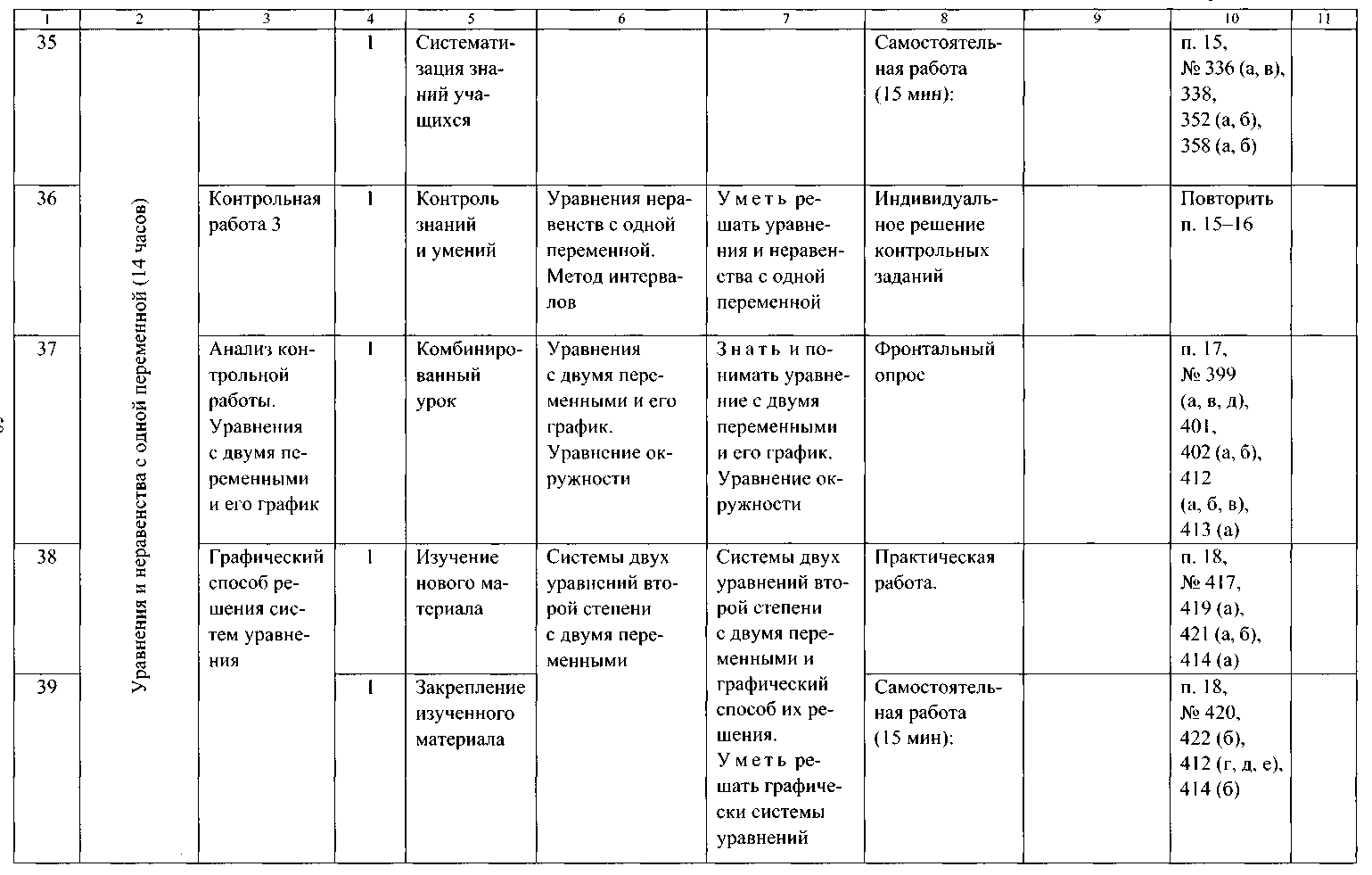
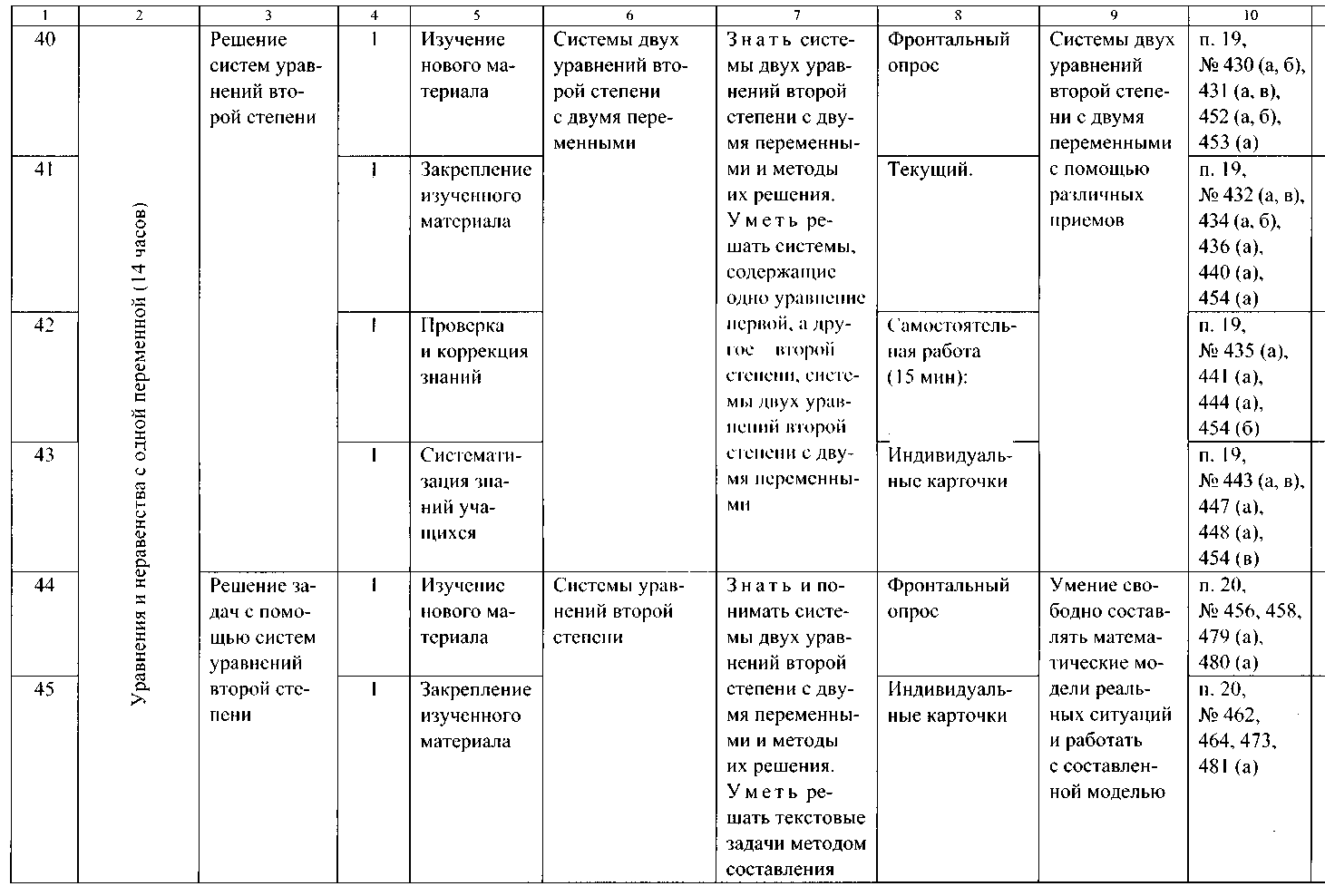
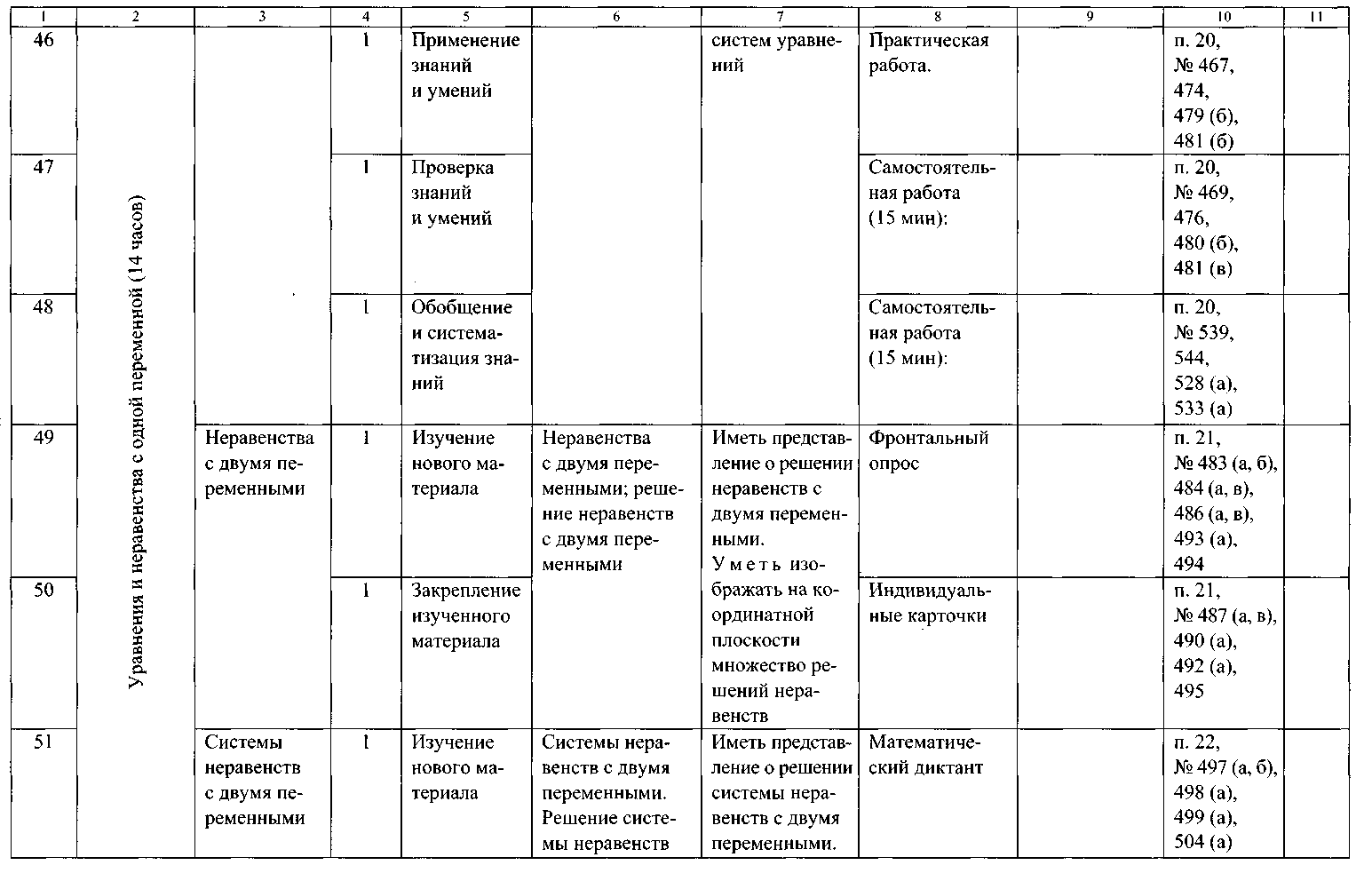
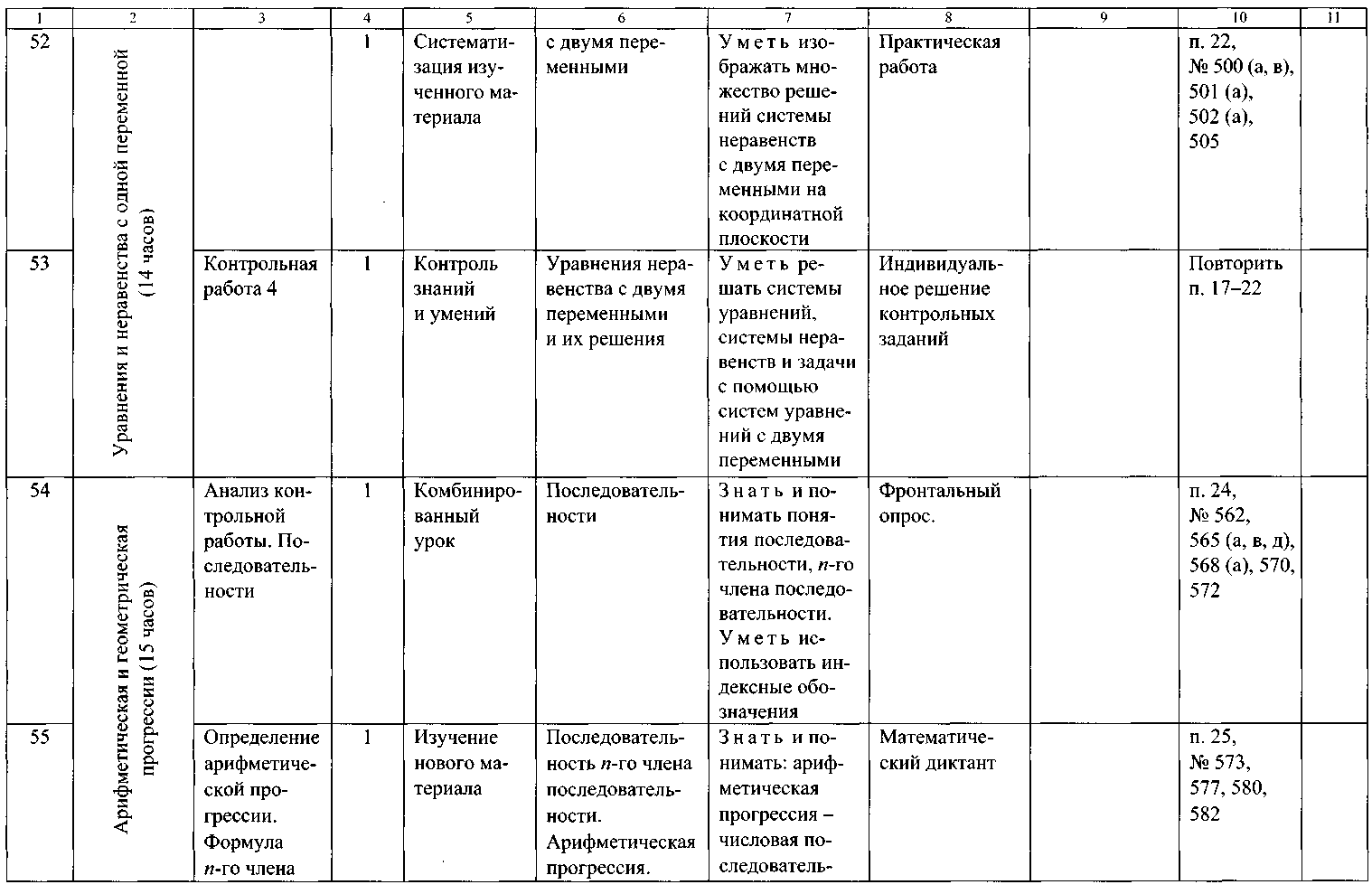
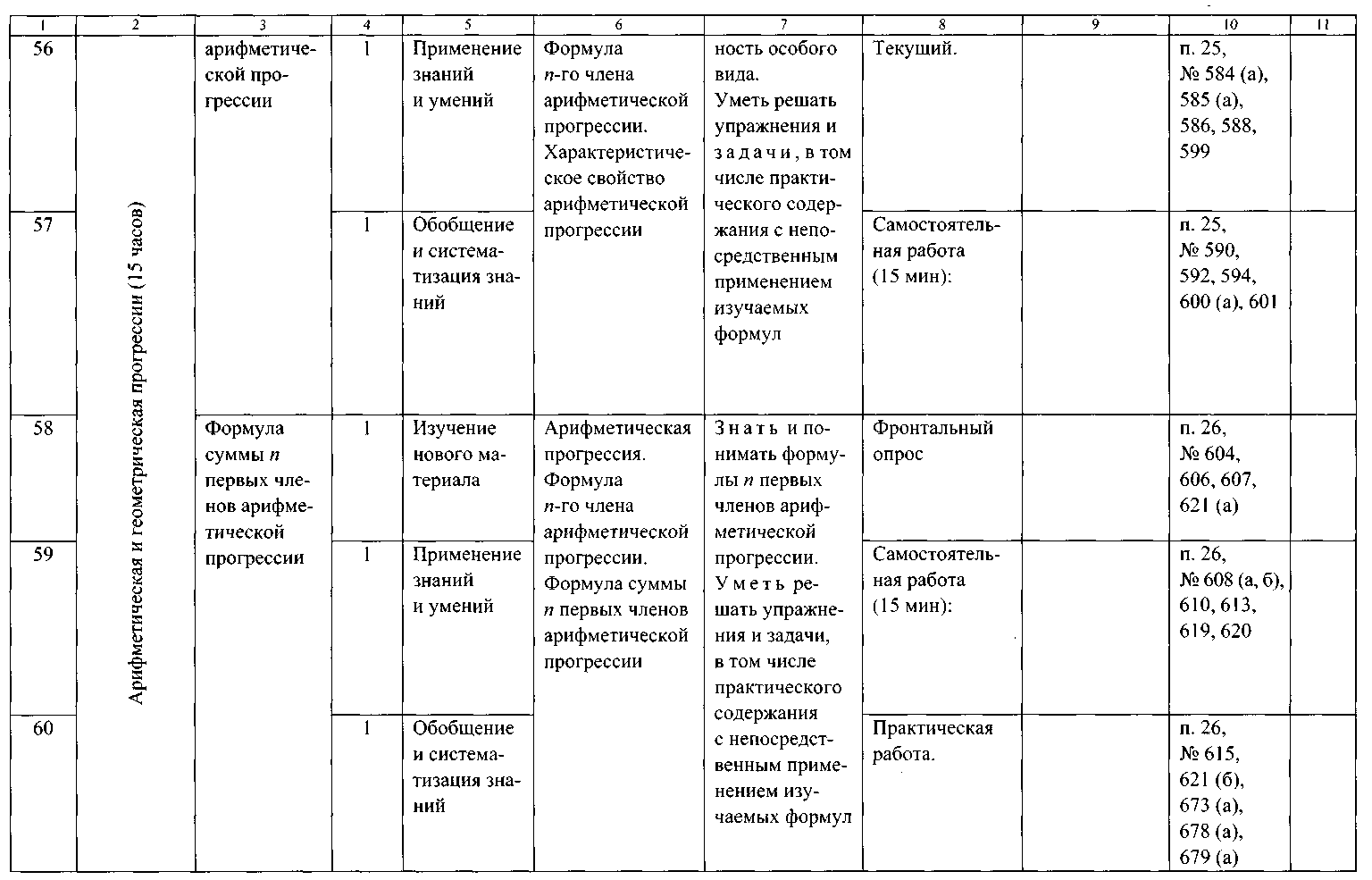
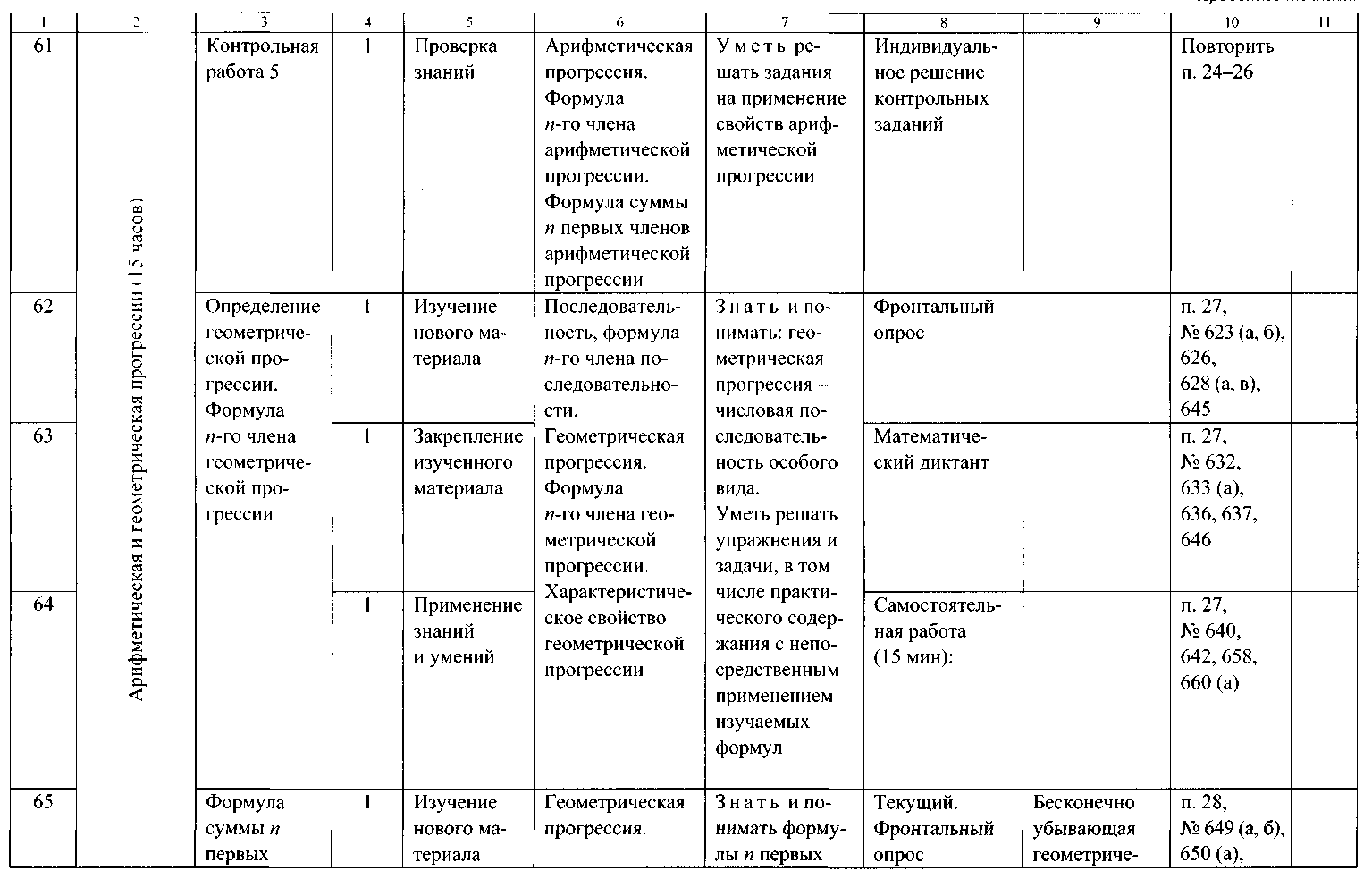
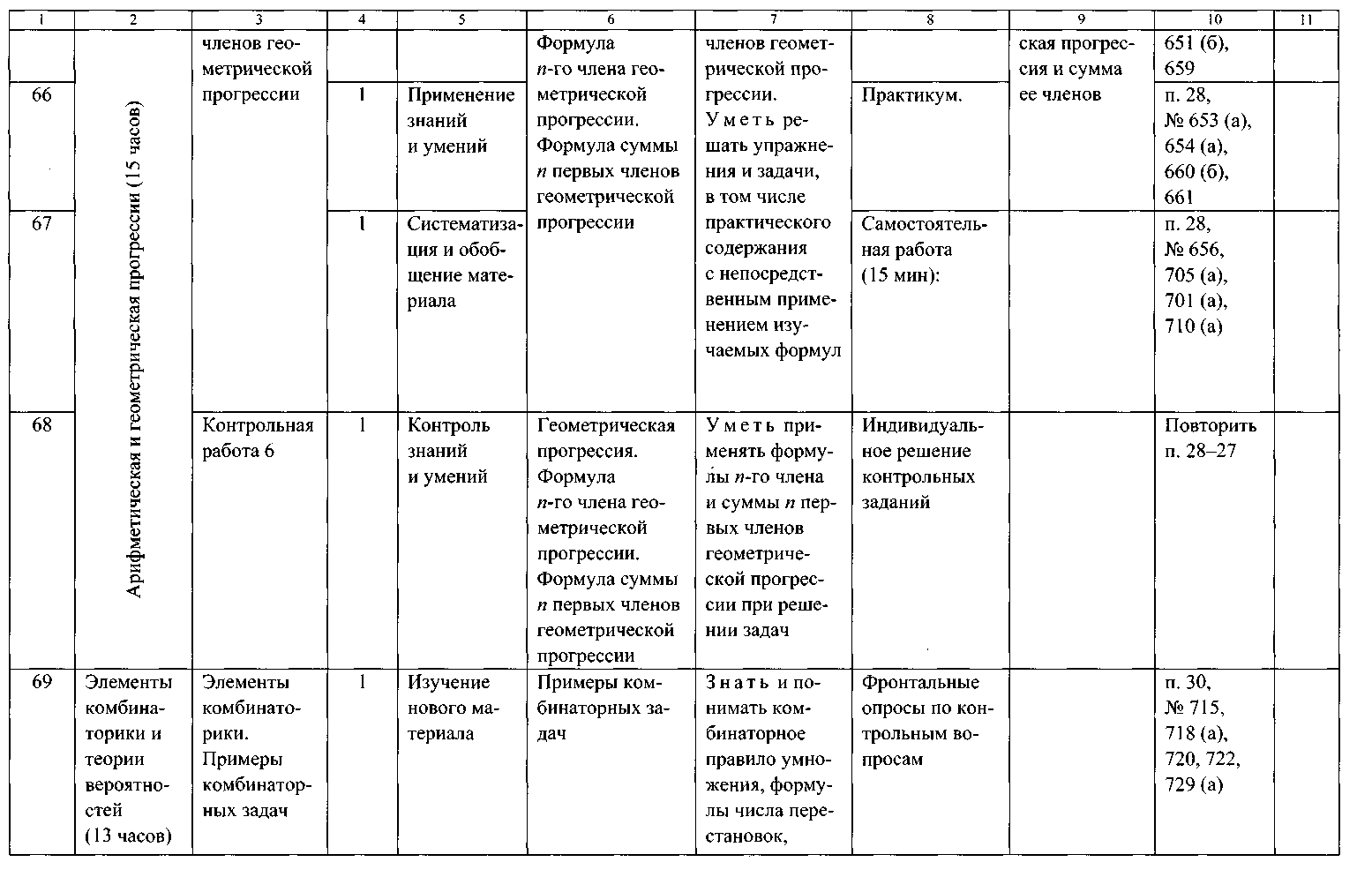
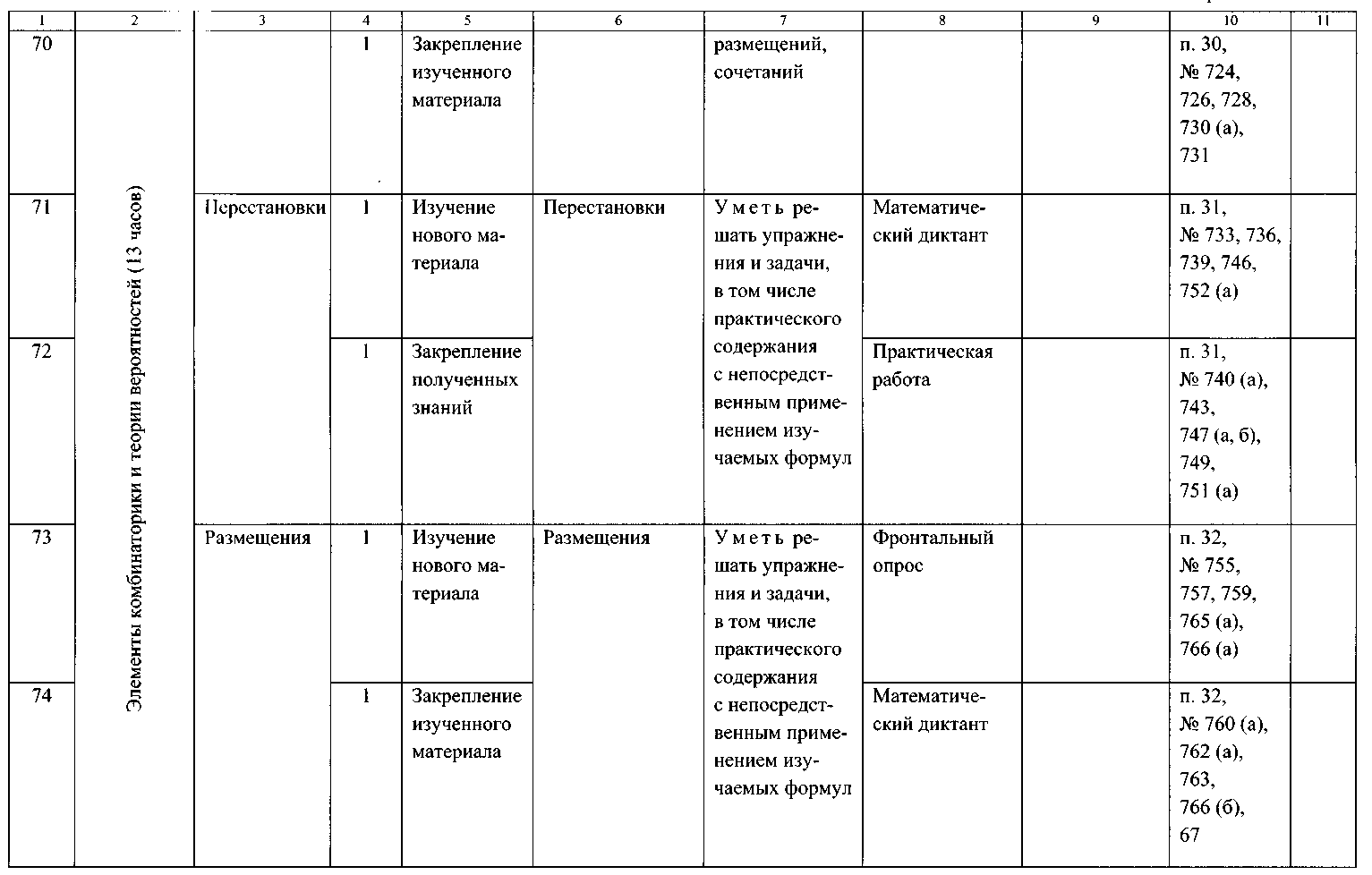
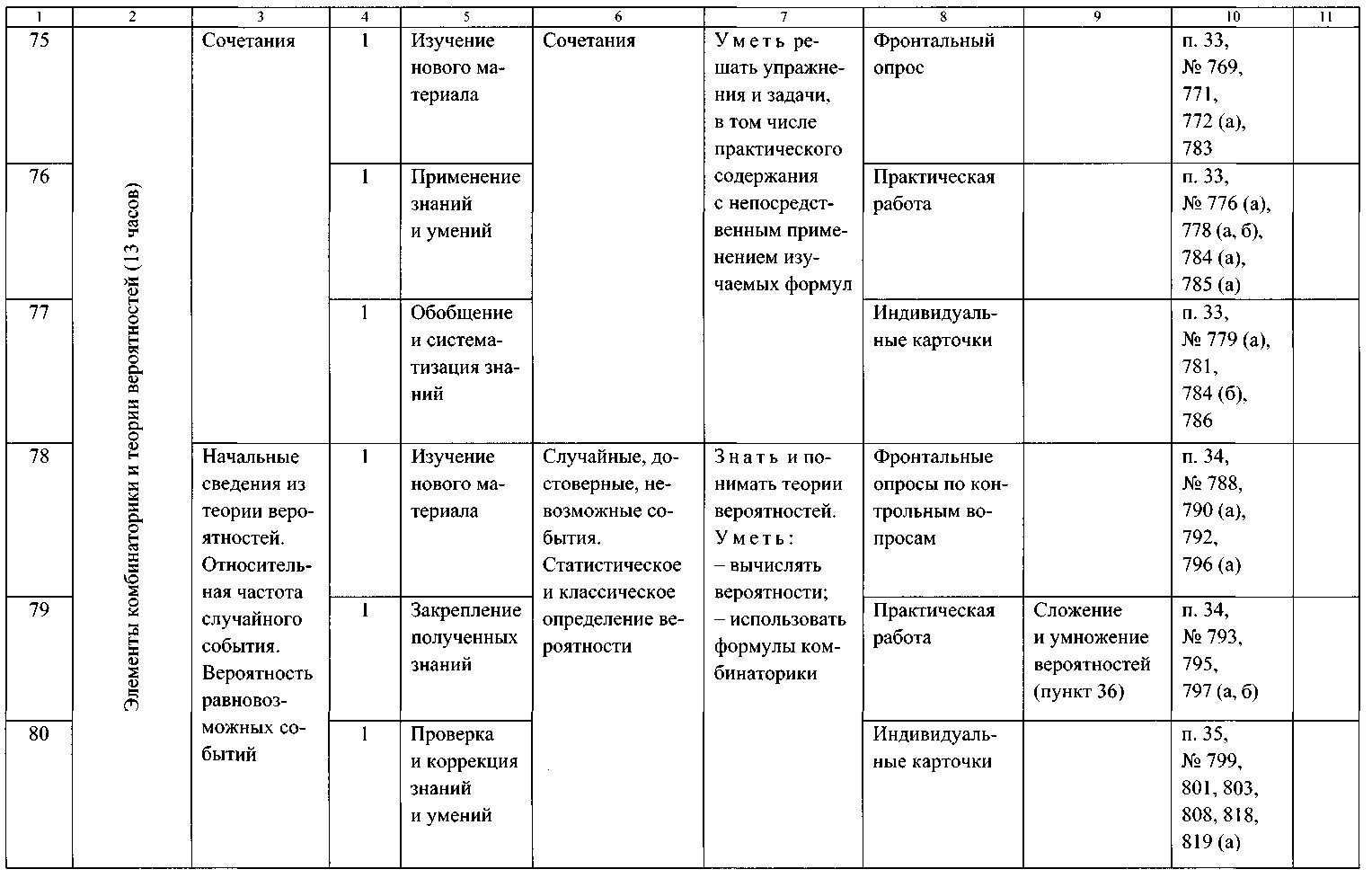
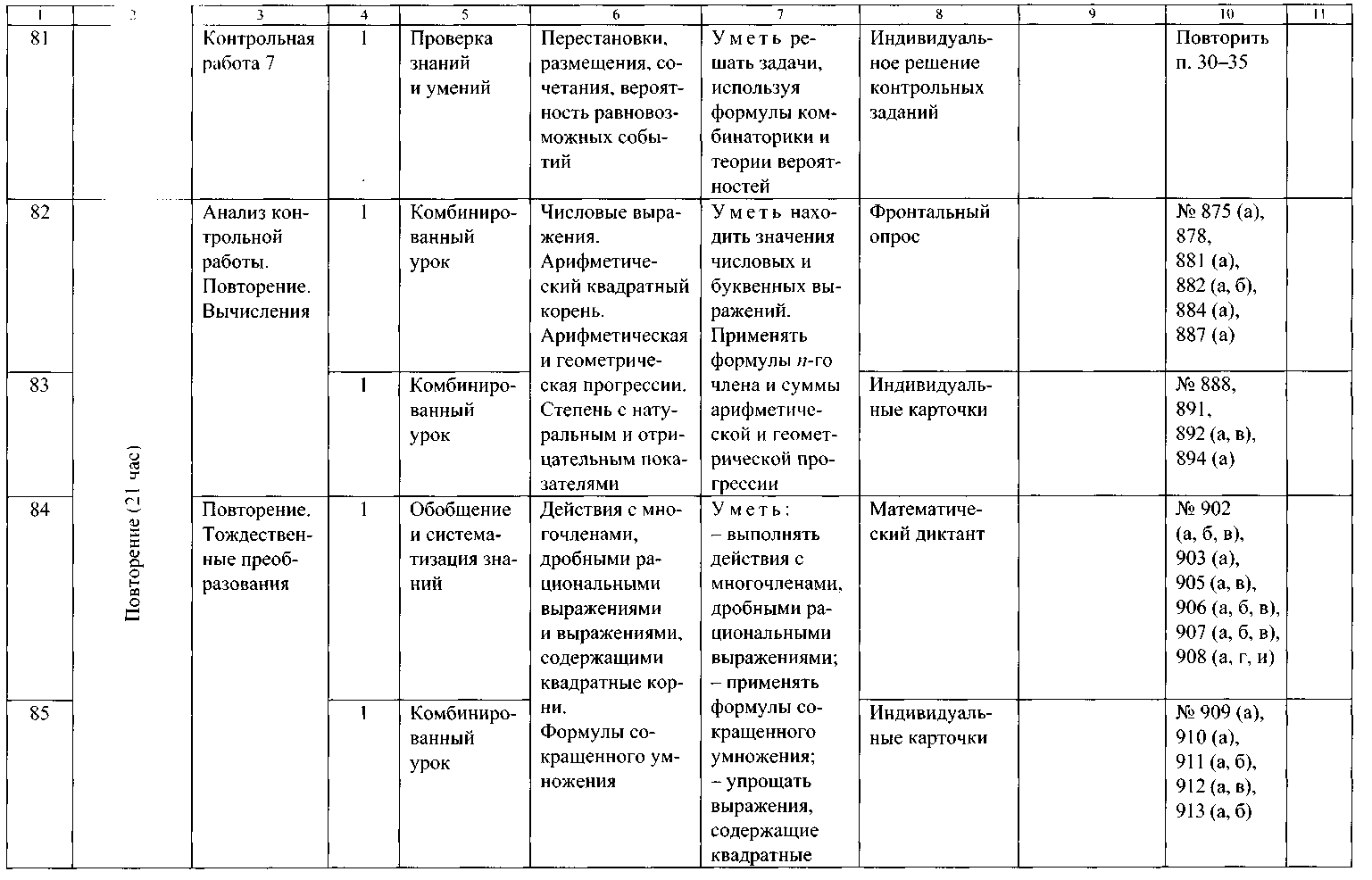
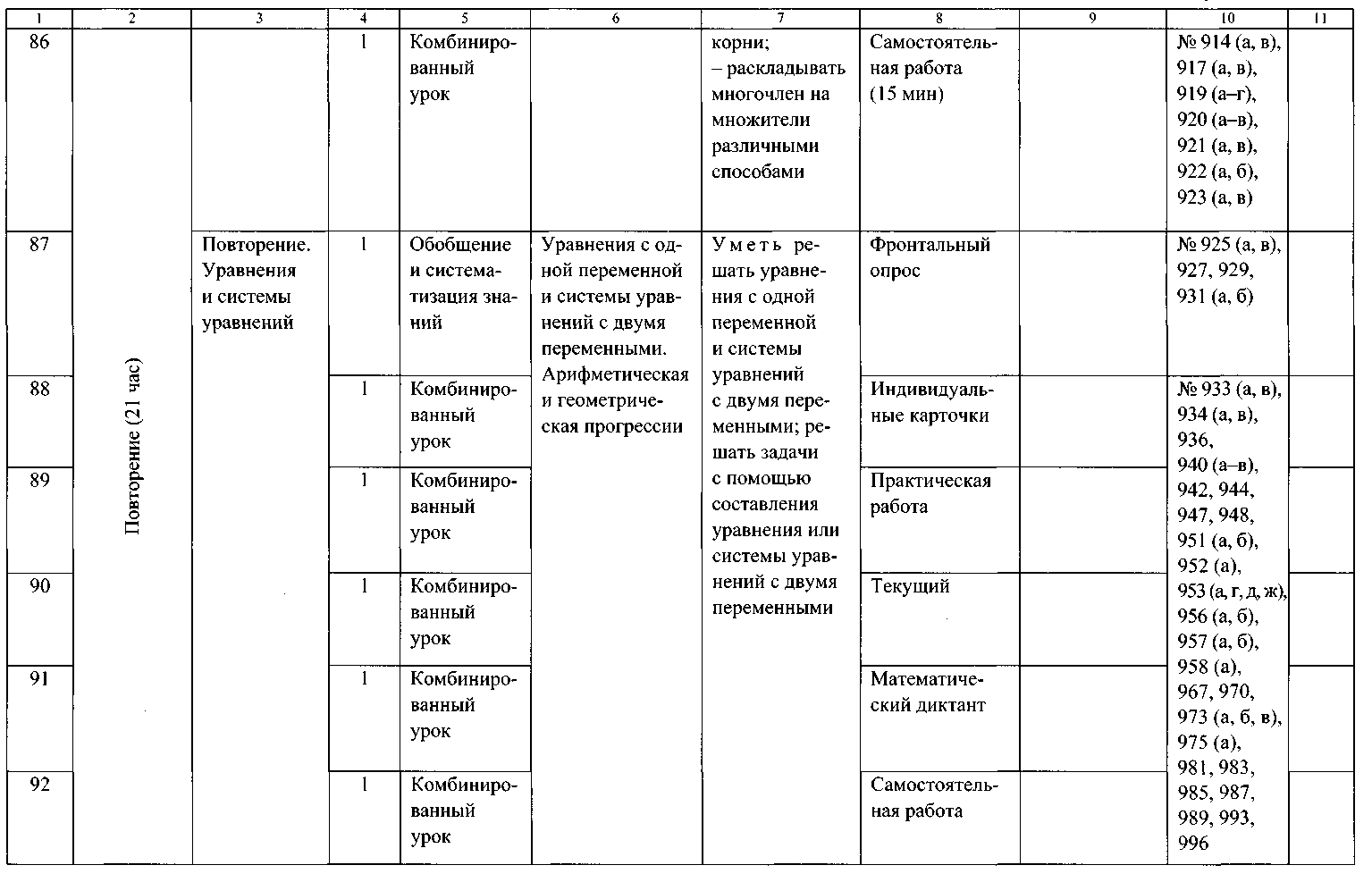
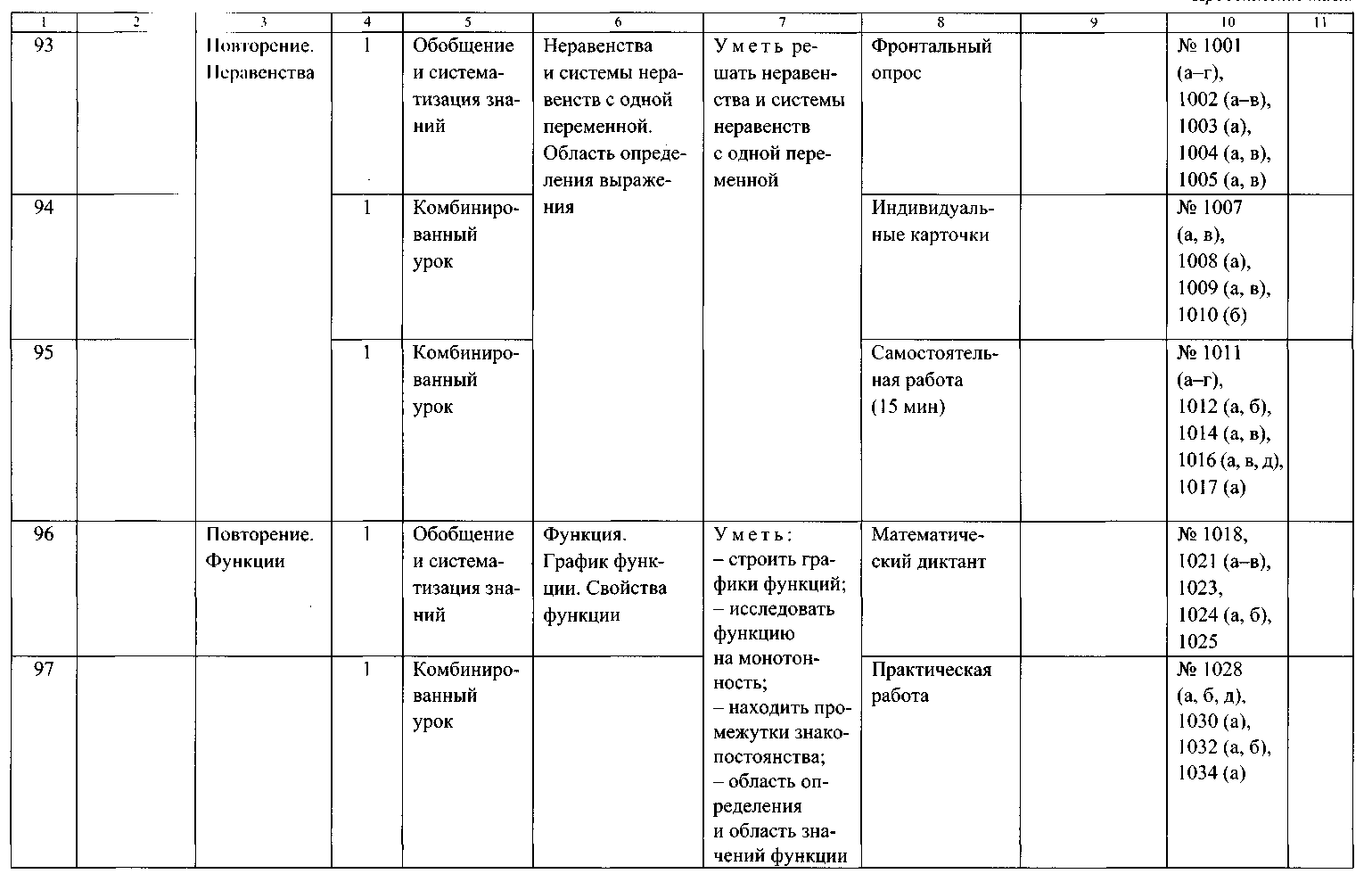
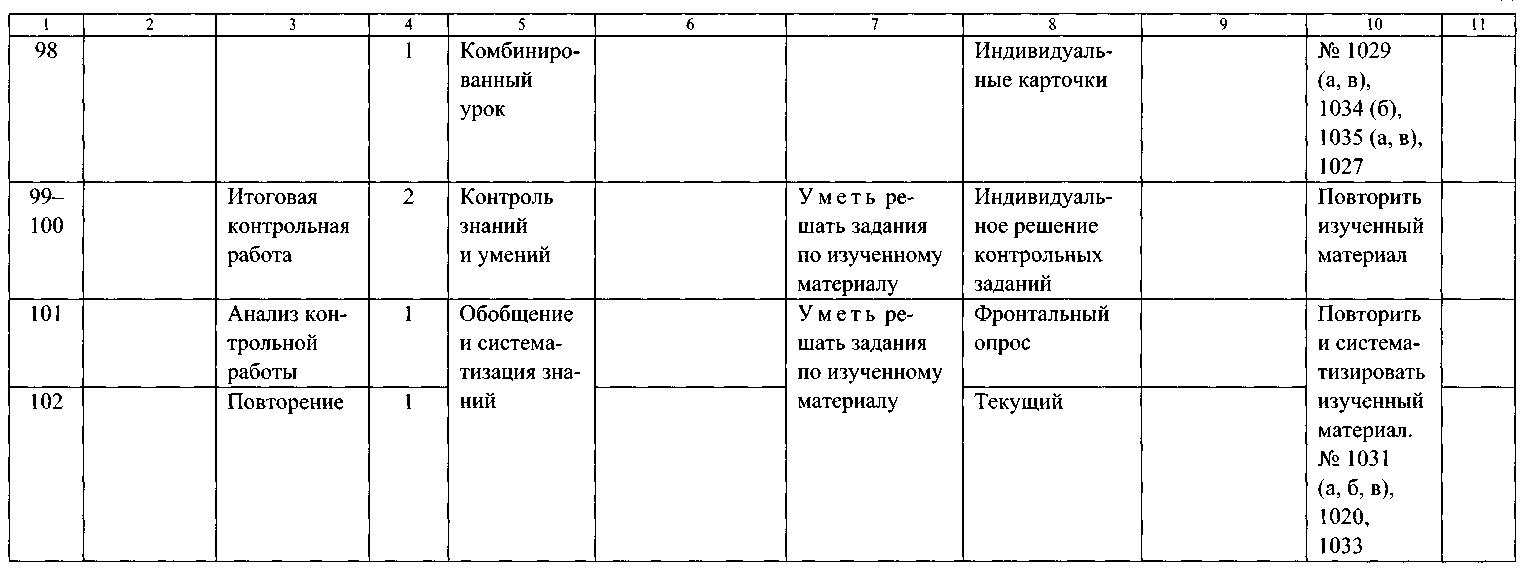
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.

ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

Номер урока	Наименова ние раздела программы	Тема урока	Коли чест во часов	Тип урока	Элементы содержания	Требования к уровню подго товки учащихся	Вид контроля	Элементы дополнитель ного содержания	Домашнее задание	Дата про веде ния
1	2	3	4	5	6	7	8	9	10	11
1-2		Функции	2	Актуализа	Функция.	Знать поня	Входной кон-	Умение сво	п. 1,№3,
		и их свойства		ция знаний	Область опреде	тие функции	троль (20 мин).	бодно читать	№ 5, 6 (а),
				и умений	ления, множест во значений функции.	и другую функ циональную терминологию.	Фронтальный опрос	графики, опи сывать свой ства функции	16, 17 (а, в), 29, 9 (а, в, д), 13, 15,
	Квадратич ная функция 22 часа				Примеры функ циональных зависимостей. Возрастание и убывание функции	Уметь правильно упот реблять функ циональную терминологию, понимать ее в тексте, в речи учителя, в формулиров		по графику	18 (а), 29 (б)
3		Функции и их свойства	1	Ознакомле ние с новым учебным материалом			Текущий.	Графики функций, со держащих переменную под знаком модуля	п. 1,2, № 17(6), 19, 22, 24 (а), 30 (а, б, в), 33,36
4-5		Функции	2	Закрепление			Практическая		п. 1,2,
		и их свойства		изученного		ке задач; нахо	работа.		№ 25 (б), 37,
				материала		дить значения			41, 30 (г, д,
						функций, за			е), 44, 53,
						данных форму			46 (а), 50 (а),
						лой, таблицей,			31 (а, б),
						графиком; решать обрат ную задачу			200 (а, б), 210,212
6		Квадратный	1	Ознакомле-	Квадратный	Знать поня	Фронтальный	Умение само	п. 3, 60, 62,
		трехчлен		ние с новым учебным материалом	трехчлен. Корни квадратно го трехчлена.	тие квадратного трехчлена, фор мулу разложе ния квадратно	опрос	стоятельно выбрать ра циональный способ разло-	72, 74 (а), 75 (а)

1	2	3	4	5	6
7			1	Закрепление изученного материала	Выделение квадрата дву члена из квад ратного трех члена.
8			1	Ознакомле-	Разложение
				ние с новым учебным	квадратного трехчлена
				материалом	на множители
9	Квадратич ная функция 22 часа		1	Закрепление изученного материала
10		Контрольная	1	Контроль	Функция.
		работа 1		знаний	Область опреде
				и умений	ления, множест во значений функции. Квадратный трехчлен. Корни квадрат ного трехчлена. Разложение квадратного трехчлена на множители

7	8	9	10	11
го трехчлена	Текущий.	жения квадрат	п. 3, № 65,
на множители.		ного трехчлена	66 (а, б),
Уметь выде		на множители	67, 74 (б),
лять квадрат			75(6)
двучлена из квадратного
двучлена из квадратного	Индивидуаль		п. 4, № 77,
трехчлена, раскладывать трехчлен на множители	ные карточки		79 (а), 80 (а, б), 87 (а), 88 (а)
трехчлена, раскладывать трехчлен на множители	Самостоятель		п. 4,
	ная работа		№83
			(а, в, д),
			84 (а),
			85 (а),
			87 (б),
			89
Уметь нахо	Индивидуаль		Повторить
дить корни	ное решение		п. 1-4
квадратного	контрольных
трехчлена	задании
и уметь рас
кладывать его
на множители

1 2