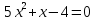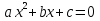Урок 9 10 Тема урока. Решение квадратных уравнений. Тип урока. Урок применения знаний, навыков и умений
 Скачать 44.57 Kb. Скачать 44.57 Kb.
|
      Урок 9 – 10 Урок 9 – 10 Тема урока. Решение квадратных уравнений. Тип урока. Урок применения знаний, навыков и умений. Дидактическая цель: повторение способов решения квадратных уравнений, проверка умений верно и рационально решать квадратные уравнения; формирование умений самостоятельно применять полученные знания при решении задач на квадратные уравнения. Развивающая цель: способствовать формированию умений применять приемы: обобщения, сравнения, выделения главного, переноса знаний в новую ситуацию; способствовать развитию математического кругозора, мышления и речи, внимания и памяти; Воспитательная цель: воспитание трудолюбия, взаимопомощи, взаимоуважения и математической культуры. Эпиграф: «Через математические знания, полученные в школе, лежит широкая дорога к огромным, почти необозримым областям труда и открытий». А. Маркушевич Ход урока 1.Мотивационная работа: Французский писатель Анатоль Франс (1844-1924) заметил: «Что учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом». Последуем совету писателя: будем на уроке активны, внимательны, будем «поглощать» знания с большим желанием, ведь они вам скоро понадобятся, впереди самостоятельная работа 2. Входной контроль Цель: актуализация опорных знаний по теме. Задание1. (фронтальный опрос)
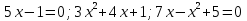 . .
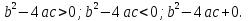
Задание 2. Ответьте на вопросы теста . Ответы запишите в тетрадь. Какое из выражений является квадратным уравнение? Вариант 1. Вариант 2.
б) 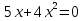 б) б) 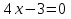 в) 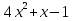 в) в) 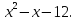 2. Какие из чисел являются корнями уравнения? Вариант 1. Вариант 2. 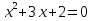 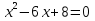 а) -1 и -2; б) 2 и – 1; в) -2 и 1 а) -4 и 2 б) 4 и – 2; в) 4 и 2.
Вариант 1. Вариант 2. 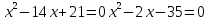 а) ( – и +) б) (– и –) в) (+ и + ) а) (+ и +) б) (– и + ) в) (– и –)
Вариант 1. Вариант 2. При 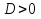 При При 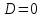 а) один б) два в) ни одного а) один б) два в) ни одного 5. Не решая уравнения, определите, сколько корней оно имеет: Вариант 1. Вариант 2. 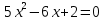 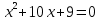 а) один б) два в) ни одного а) один б) два в) ни одного Взаимопроверка: Вариант 1. Вариант 2.
5) в 5) б 3. Осмысление учащимися составления и решения квадратного уравнения по условию задачи. № 560 учебник стр.131. Решение. Пусть ширина прямоугольника х см, тогда его длина (х +4) см. Площадь равна х(х+ 4) см2, что по условию задачи 60 см2. Составим уравнение: х(х +4) = 60; х1 = 6, х2 = - 10. Второй корень не подходит по смыслу задачи, значит, ширина прямоугольника 6 см, а длина 6 + 4 = 10 см. Ответ: 6см; 10 см. 4.Тренировочные упражнения № 562. Решается с комментариями. № 567 Решается самостоятельно в парах. Затем с места ученик комментирует решение задачи. 5.Самостоятельная работа (Приложение 2) 6.Итог урока. Рефлексия. Домашнее задание. Рефлексия Достигли ли вы цели урока? В какой степени? Оцените свою работу на уроке: «Отлично», «хорошо» или «удовлетворительно». Д/з п. 23 № 563, №590, № 518(д,е) Итог урока. Сегодня мы провели большую работу на уроке, которая подняла вас на новый уровень знаний. И хотелось бы закончить урок такими словами: «Образование – это не количество прочитанных книг, а количество понятых». Приложение 2 Самостоятельная работа
Задания №1 оценивается по 1б за каждое Задание 32 - №3 по 3б. Всего 10 баллов. 4 – 5 баллов - «3» 6 – 8 баллов - «4» 9 – 10 - «5» | ||||||||||||||||||
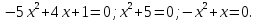
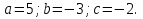
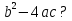
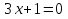 a)
a)