Производная и ее геометрический смысл

Скачать 71.41 Kb. Название Производная и ее геометрический смысл Дата 02.03.2016 Размер 71.41 Kb. Тип Урок

«МАТЕМАТИЧЕСКАЯ ИГРОТЕКА» (УРОК-ЗАЧЕТ) Алгебра и начала анализа, 11 класс ТЕМА «ПРОИЗВОДНАЯ И ЕЕ ГЕОМЕТРИЧЕСКИЙ СМЫСЛ» ЦЕЛЬ УРОКА: 1-обобщить знания учащихся по данной теме; 2-подготовить к контрольной работе. Организация урока Учитель разбивает класс на 4-5 групп по 4-5 учащихся в зависимости от количества учащихся в классе. Команды составлены по уровню знаний.1 команда состоящая из сильных учащихся является консультантами(заранее подготовлена) Ход игры «ЛОТО» (от 3 до5 минут) консультанты по одному расходятся в группы. У каждой группы конверт, в котором лежат большая карточка с вопросами и маленькие карточки с номерами ( от 1 до 8-12). Номеру соответствует свой вопрос. Учащиеся по очереди достают карточку и отвечают на вопрос (правильный ответ-1 балл, передача ответа -0,5балла) 1-определение производной функции 2-определение предела функции 3-определение непрерывной функции 4-Производная суммы функций 5-производная произведения функций 6-производная частного функций 7-производная сложной функции 8-механический смысл производной 9-геометрический смысл производной 10-уравнение касательной к графику дифференцируемой функции 11-производная Сf(х) 12-определение разностного отношения Консультант выставляет полученные баллы в карточку учета: № Список учащихся группы Лото(баллы) Гонка за лидером эрудит Общий итог за конкурсы Своя игра 1 2 3 4 итого 2- Гонка за лидером (3 минуты) На отдельном листе бумаги воспроизвести формулы производных элементарных функций. Один записывает, а остальные помогают. Консультанты проверяют формулы( формула-1 балл) выставляют в карточку учета. 3- Эрудит(15минут) Команда получает 4 карточки-тесты с заданиями(правильный ответ +).Тесты на 2 варианта по уровню сложности. Количество тестов можно увеличить или уменьшить. Консультанты проверяют (правильный ответ-1 балл) и выставляют в карточку учета. Объявляют итог трех конкурсов. 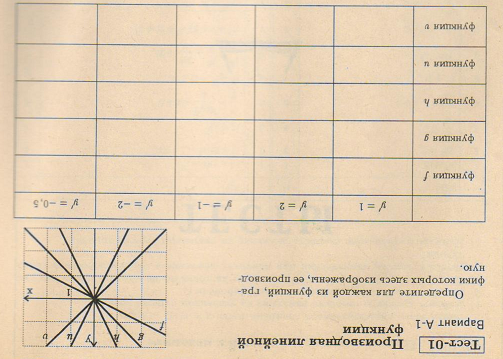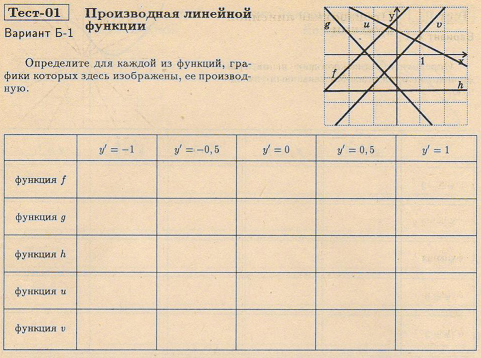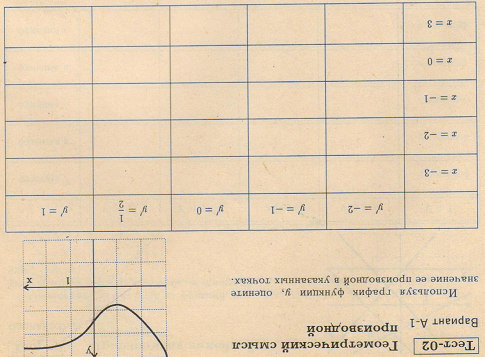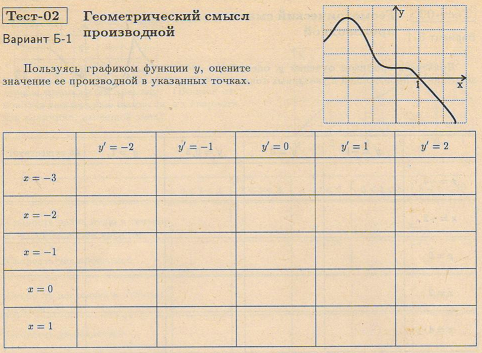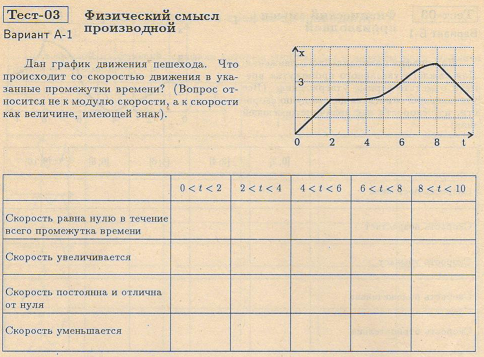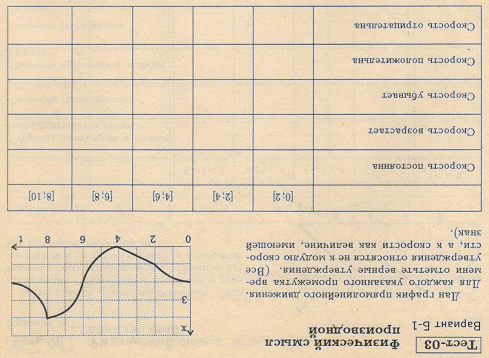Ключи к тестам. Т-1 А-1 Т-1 Б-1 Т-2 А-1 Т-2 Б-1 + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + Т-3 А-1 Т-3 Б-1 Т-5 А-1 Т-5 Б-1 4- Своя игра (15 минут) Все учащиеся получают карточки с заданиями и самостоятельно решают . Проверяет учитель. Карточка №1 Дана функция у=f(х) Найдите угловой коэффициент касательной к графику этой функции в точке с абсциссой х0 Найдите точки, в которых угловой коэффициент касательной равен числу k Напишите уравнение касательной к графику функции в точке с абсциссой х0 У=х2+4, х0=1, k=4 Карточка №2 Дана функция у=f(х) Найдите угловой коэффициент касательной к графику этой функции в точке с абсциссой х0 Найдите точки, в которых угловой коэффициент касательной равен числу k Напишите уравнение касательной к графику функции в точке с абсциссой х0 У=х 2/4 -3 х0=2, k=1/2 Карточка №3 Дана функция у=f(х) Найдите угловой коэффициент касательной к графику этой функции в точке с абсциссой х0 Найдите точки, в которых угловой коэффициент касательной равен числу k Напишите уравнение касательной к графику функции в точке с абсциссой х0 У=3х2-6х+1, х0=0, k=6 Карточка №4 Дана функция у=f(х) Найдите угловой коэффициент касательной к графику этой функции в точке с абсциссой х0 Найдите точки, в которых угловой коэффициент касательной равен числу k Напишите уравнение касательной к графику функции в точке с абсциссой х0 У=х2(х-2)2, х0=1, k=0 Карточка №5 Дана функция у=f(х) Найдите угловой коэффициент касательной к графику этой функции в точке с абсциссой х0 Найдите точки, в которых угловой коэффициент касательной равен числу k Напишите уравнение касательной к графику функции в точке с абсциссой х0 У=х2(х-2)2, х0=1, k=0 Карточка №6 Дана функция у=f(х) Найдите угловой коэффициент касательной к графику этой функции в точке с абсциссой х0 Найдите точки, в которых угловой коэффициент касательной равен числу k Напишите уравнение касательной к графику функции в точке с абсциссой х0 У=Sin2х, х0=п/4, k=0 Карточка №7 Дана функция у=f(х) Найдите угловой коэффициент касательной к графику этой функции в точке с абсциссой х0 Найдите точки, в которых угловой коэффициент касательной равен числу k Напишите уравнение касательной к графику функции в точке с абсциссой х0 У=2lnх, х0=1, k=4 На следующем уроке учитель выставляет оценку (с учетом конкурсов) каждому ученику.