Программа по алгебре в 9 классе на 3 часа в неделю (всего 102 часа)
 Скачать 490.58 Kb. Скачать 490.58 Kb.
|
Содержание обучения
Содержание практической деятельности (контрольно-измерительный материал) 1).Тематика лабораторных и практических работ с заданиями (вариантами заданий) 3).Тематика докладов, рефератов и иных видов самостоятельной работы учащихся. 4).Варианты контрольных работ, тестовых заданий с критериями оценок. Контрольная работа №1 по теме: «Функции и их свойства» Вариант 1 А1. Дана функция А2. Найдите нули функции А3. Разложите на множители квадратный трехчлен: А 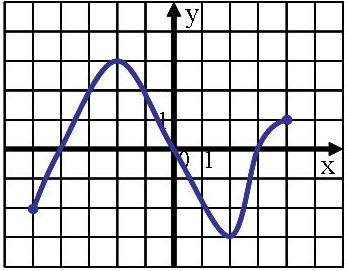 4. Сократите дробь: 4. Сократите дробь: 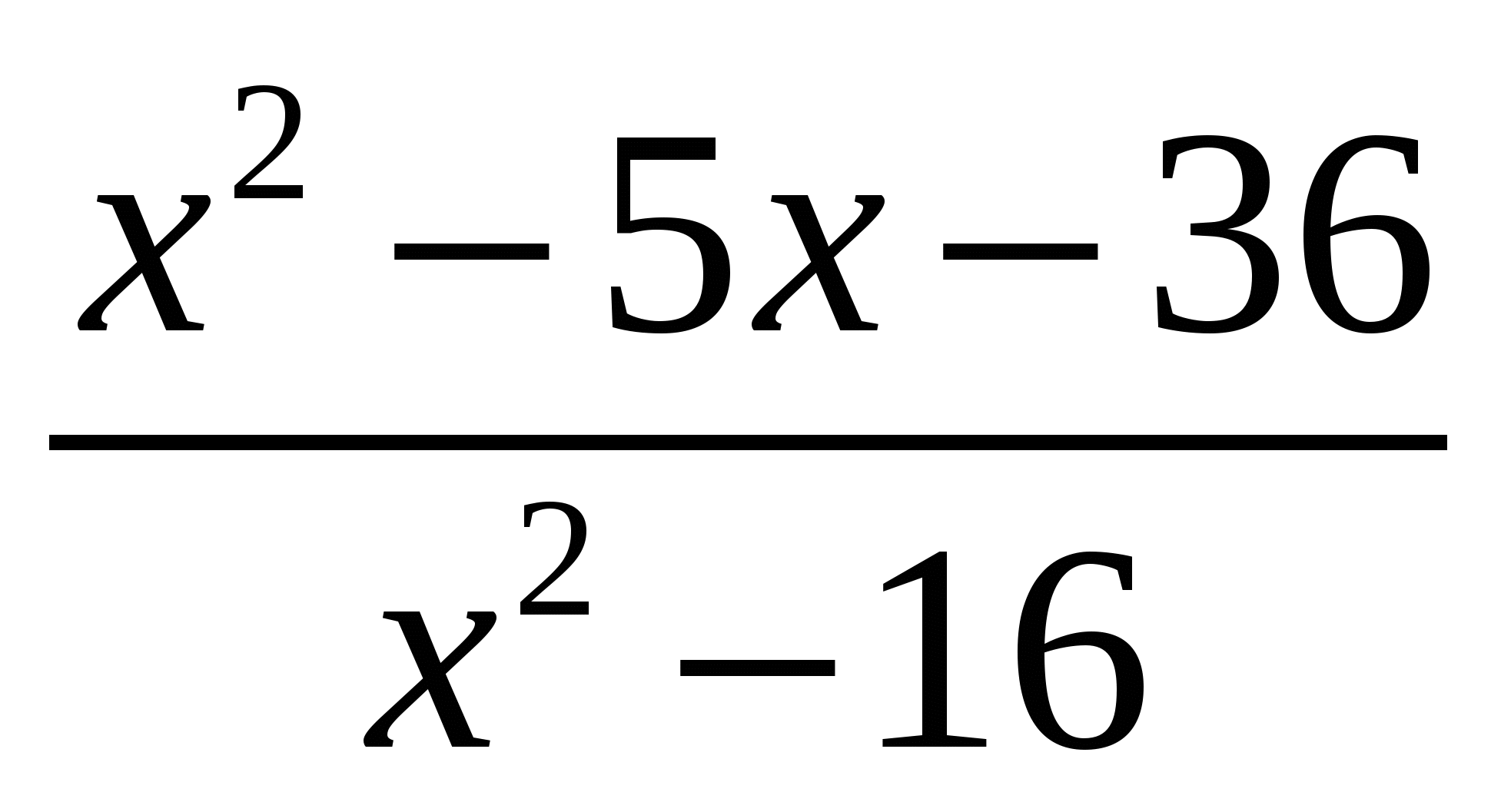 . .__________________________________________ В1. Область определения функции Вариант 2 А1. Дана функция А2. Найдите нули функции А3. Разложите на множители квадратный трехчлен: А 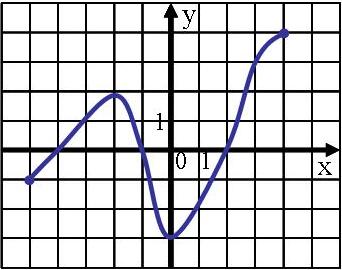 4. Сократите дробь: 4. Сократите дробь: 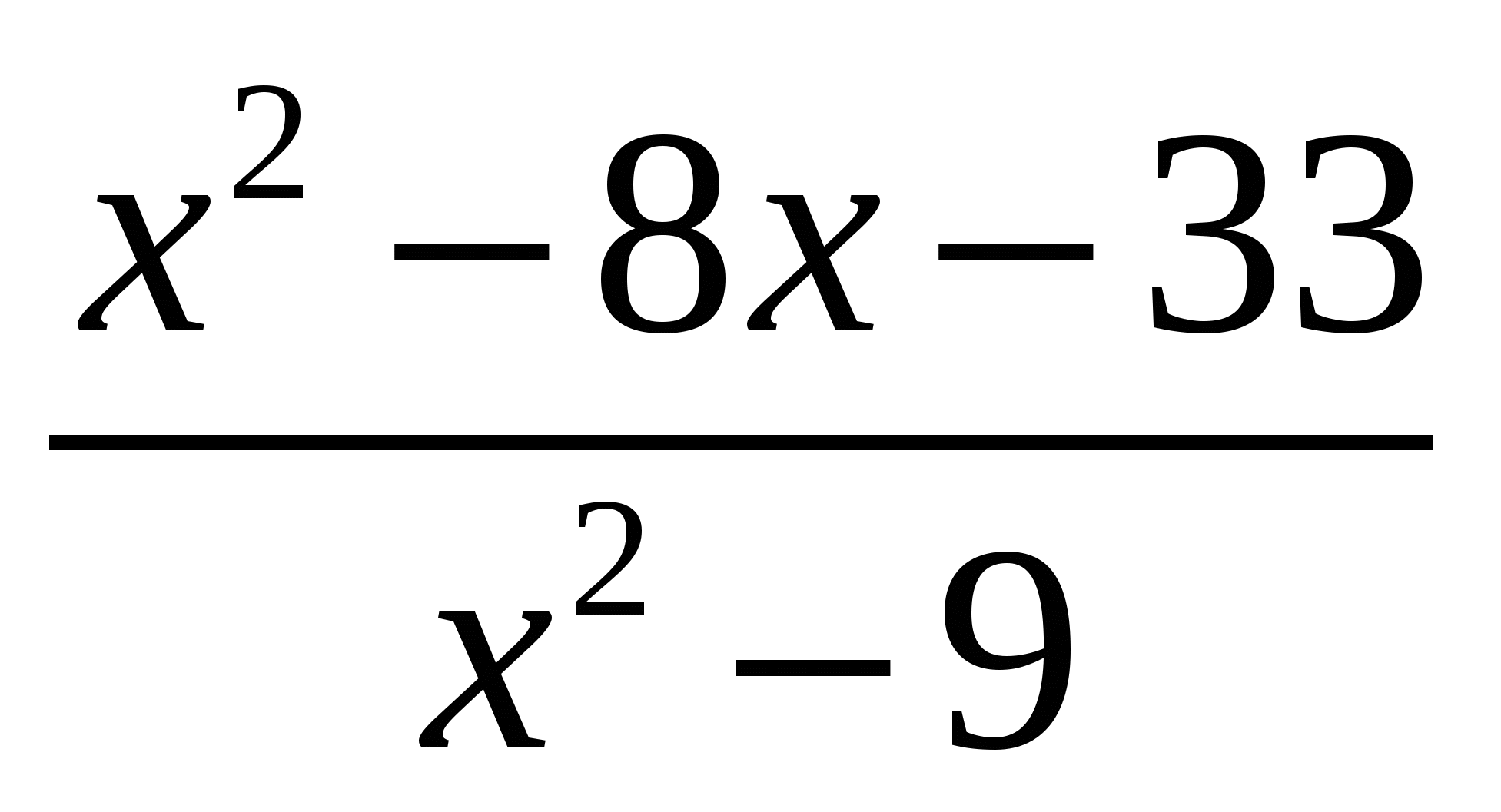 . .___________________________________________ В1. Область определения функции [-5;4]. Найдите нули функции, промежутки убывания и возрастания, область значений функции. Контрольная работа №2 по теме: «Квадратичная функция» Вариант 1 А1. Найдите значение квадратичной функции А2. Найдите наименьшее значение функции А3. Постройте график функции Определите: а) значения х, при которых функция возрастает; убывает; б) нули функции; г) значения х, при которых функция отрицательна; положительна. ________________________________________ В1. Найдите область значений функции В2. Не выполняя построения, определите, пересекаются ли парабола Вариант 2 А1. Найдите значение квадратичной функции А2. Найдите наибольшее значение функции А3. Постройте график функции Определите: а) значения х, при которых функция возрастает; убывает; б) нули функции; г) значения х, при которых функция отрицательна; положительна. ________________________________________ В1. Найдите область значений функции В2. Не выполняя построения, определите, пересекаются ли парабола Контрольная работа №3 по теме: «Уравнения и неравенства с одной переменной» Вариант 1 А1. Решите уравнение: А2. Решите неравенства: В1. Решите уравнение В2. Решите уравнение C1. Решить уравнение Вариант 2 А1. Решите уравнение: А2. Решите неравенства: В1. Решите уравнение В2. Решите уравнение C1. Решить уравнение Нормы оценок: «3»- любые 3А(из 6 заданий), 4» - 2А + 1В, «5» - 2 Контрольная работа №4 по теме: «Уравнения и неравенства с двумя переменными» Вариант 1 А1. Решите систему уравнений: а) 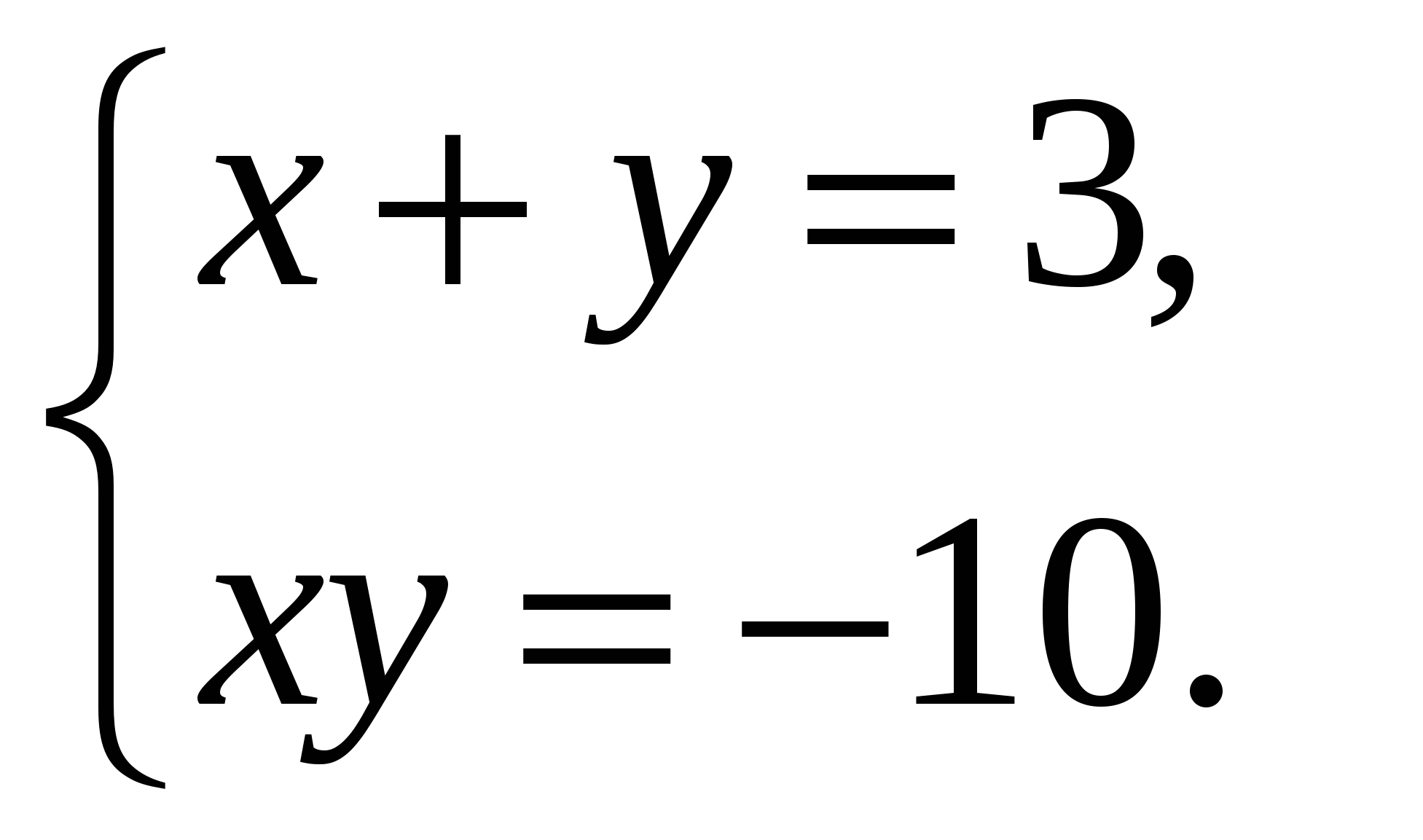 б) б) 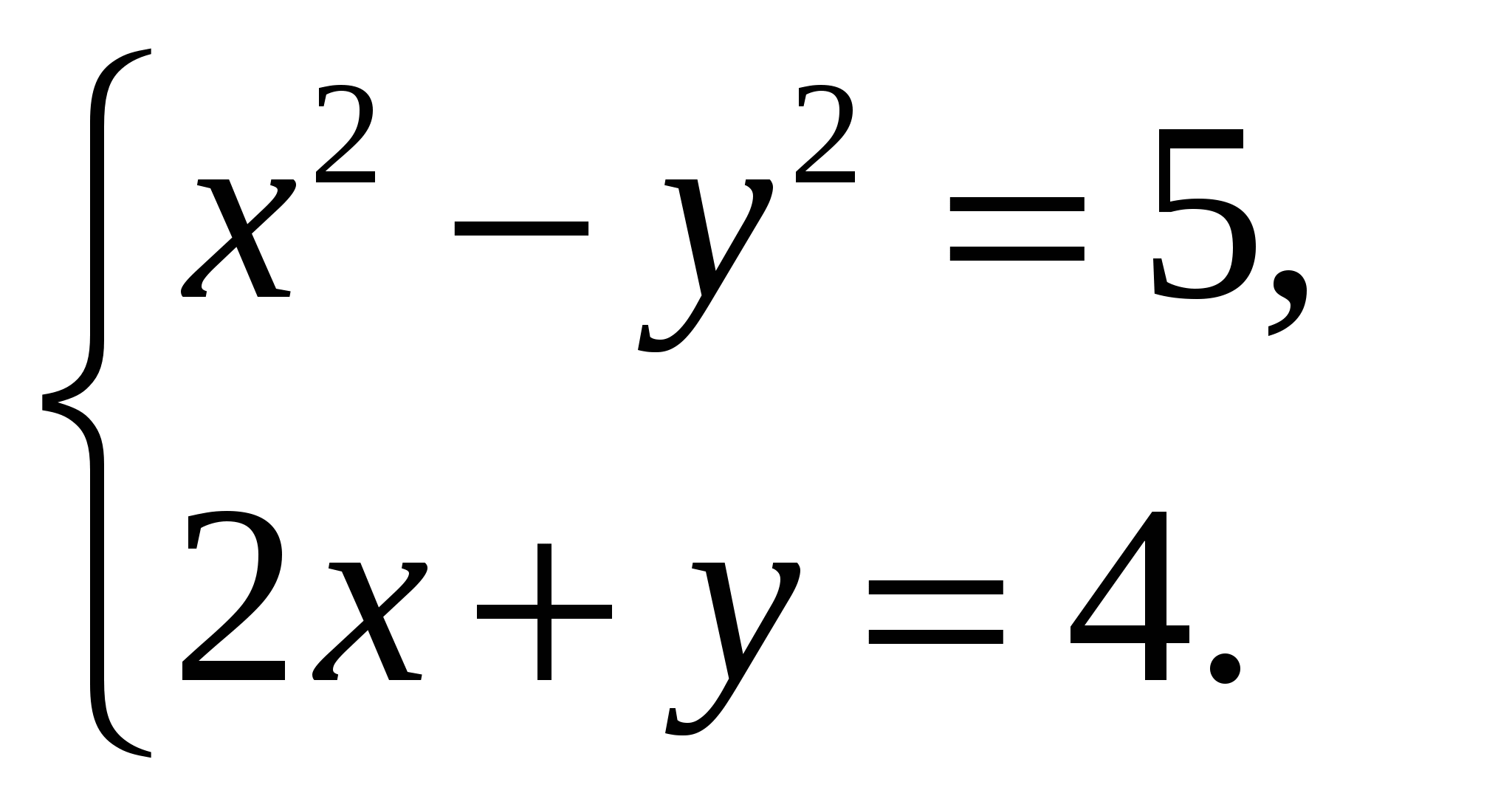 А2. Периметр прямоугольника равен 28 м, а его площадь равна 40м2. Найдите стороны прямоугольника. А3. Изобразите на координатной плоскости множество решений неравенства А4. Изобразите на координатной плоскости множество решений неравенства 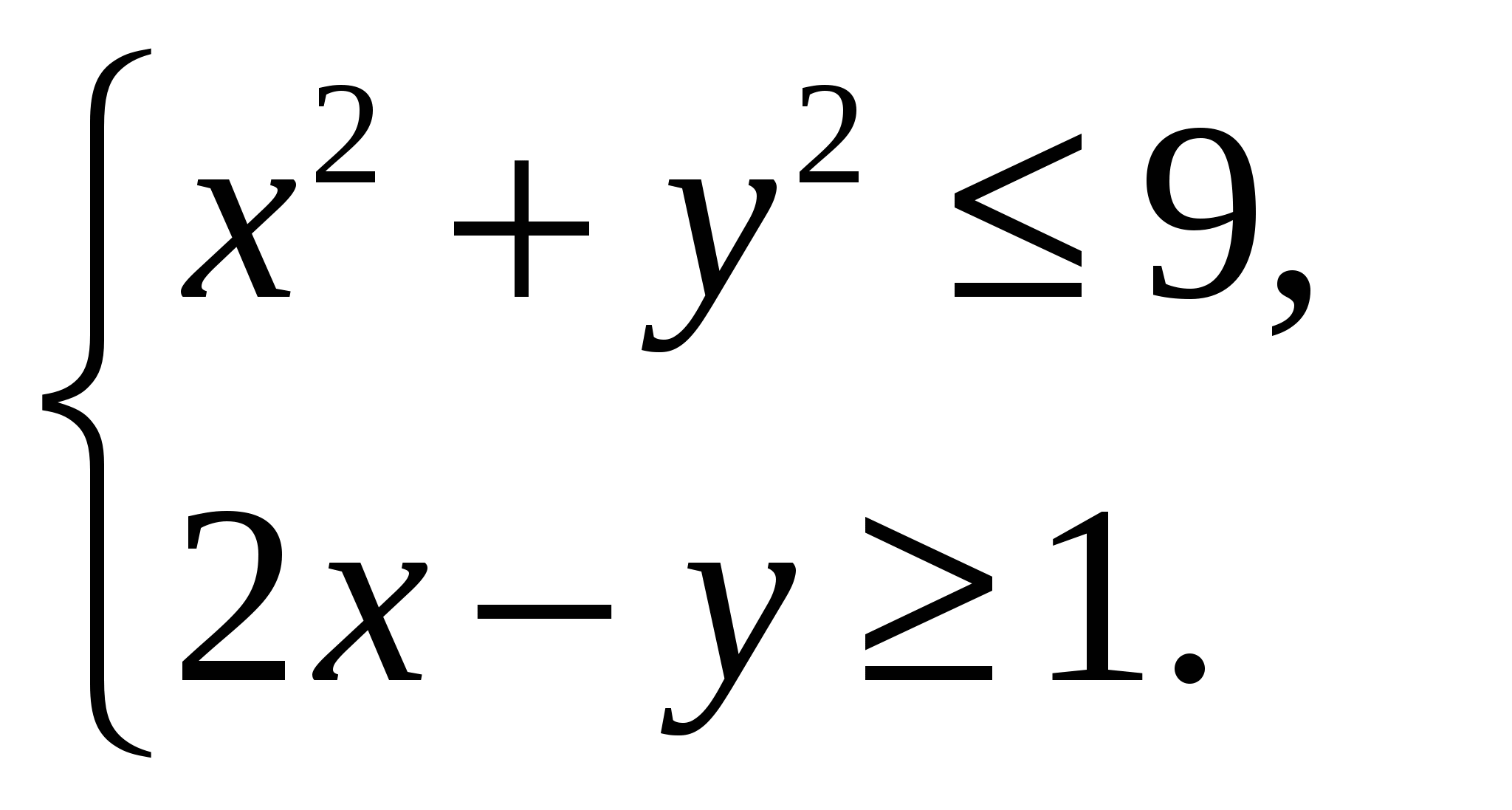 В1. Не выполняя построения, найдите координаты точек пересечения параболы Вариант 2 А1. Решите систему уравнений: а) 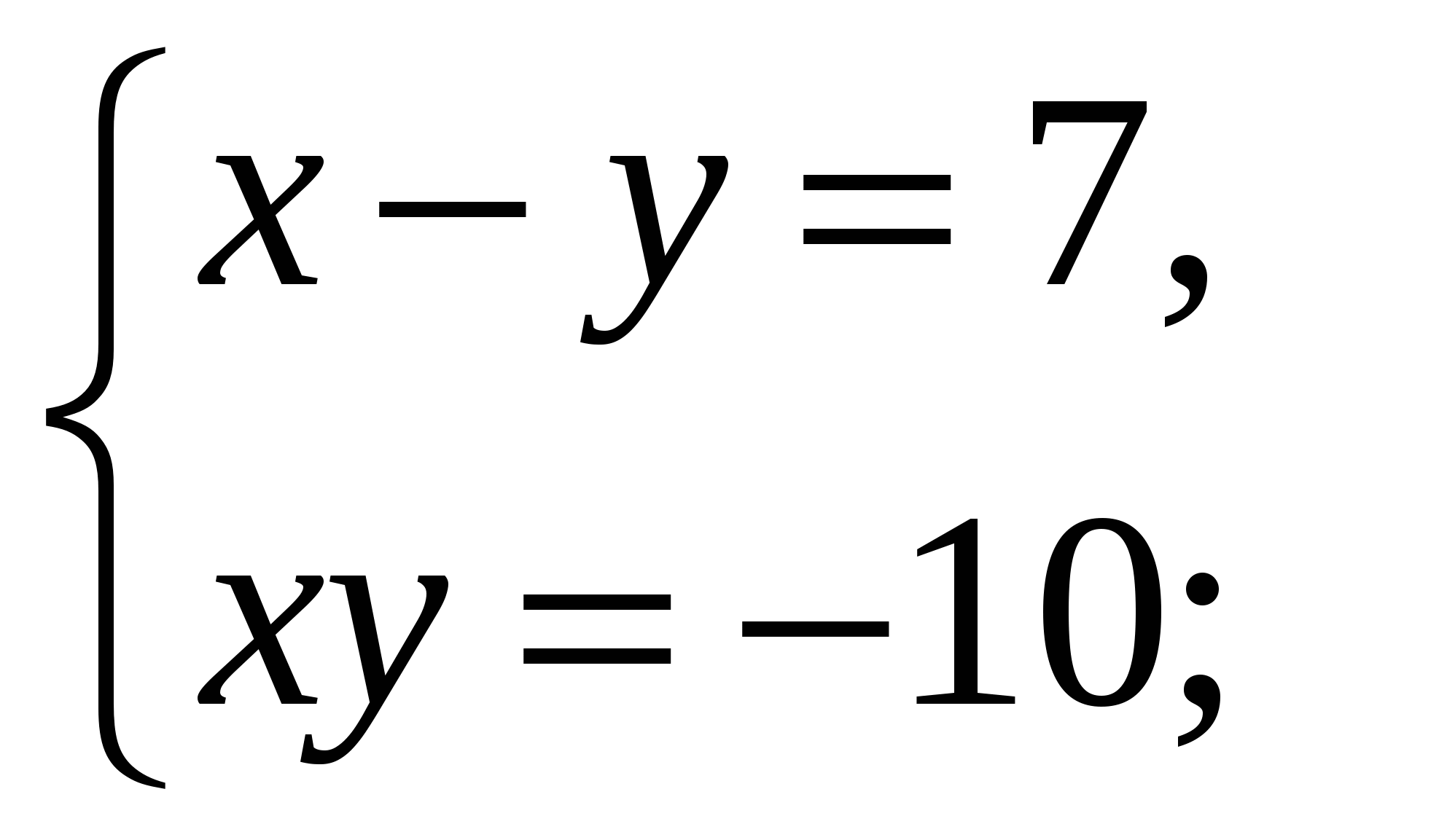 б) б) 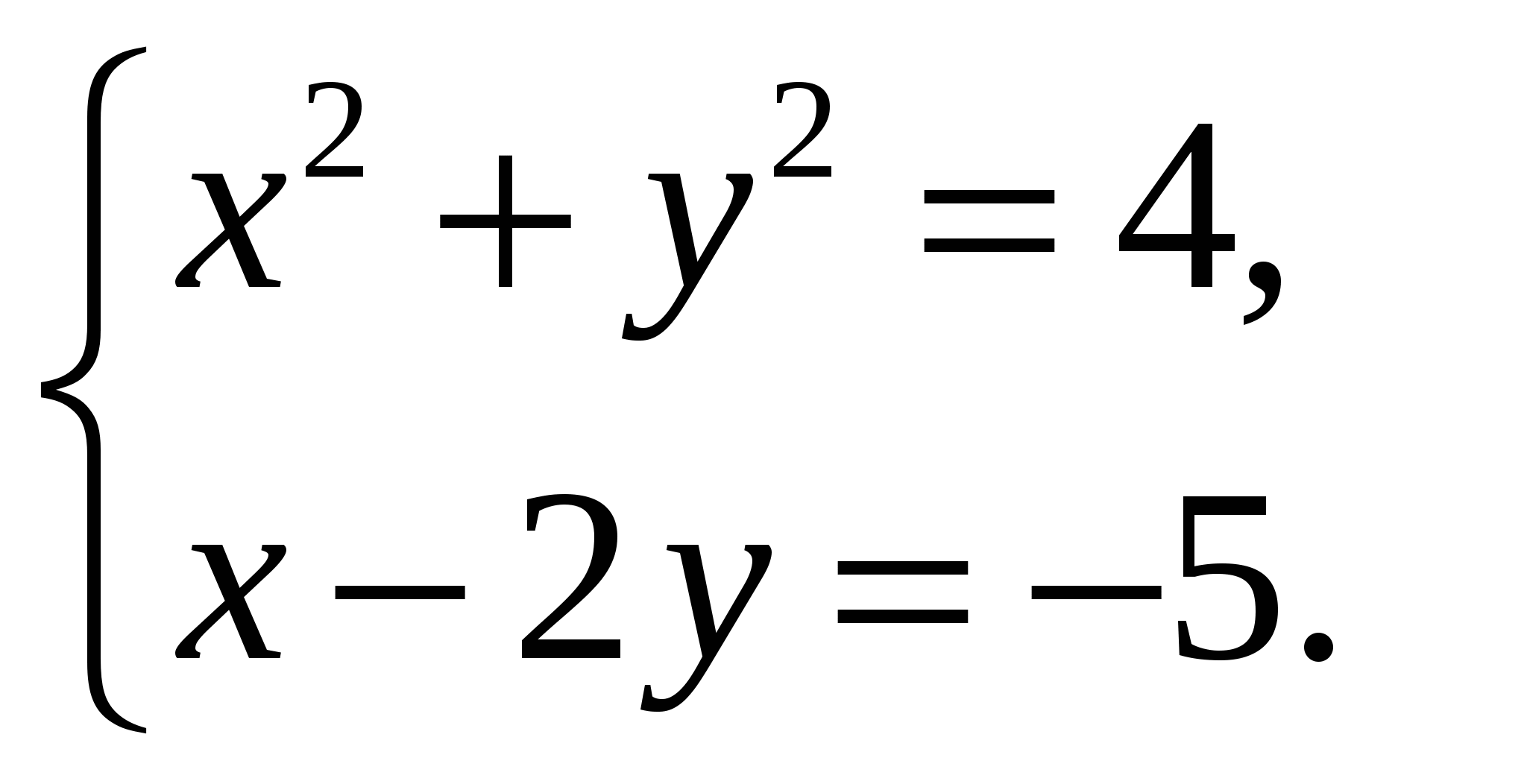 А2. Одна из сторон прямоугольника на 2 см больше другой стороны. Найдите стороны прямоугольника, если его площадь равна 120 см2. А3. Изобразите на координатной плоскости множество решений неравенства А4. Изобразите на координатной плоскости множество решений неравенства 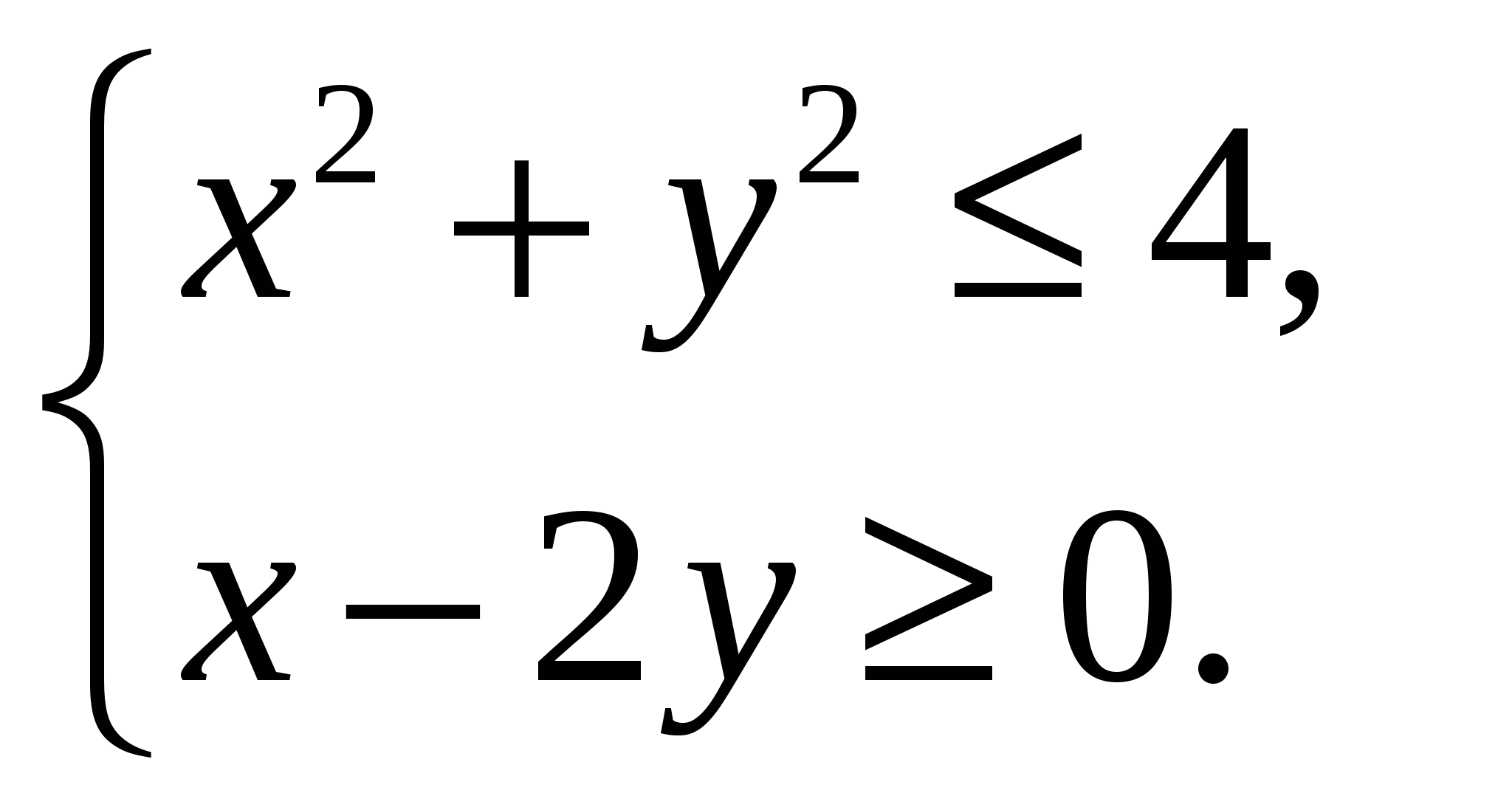 В1. Не выполняя построения, найдите координаты точек пересечения параболы Нормы оценок: «3»- любые 3А(из 5 заданий), 4» - 5А, «5» - 4А + 1В. Контрольная работа №5 по теме: «Арифметическая и геометрическая прогрессии» Вариант 1 А1. Выпишите три следующих члена арифметической прогрессии: а) 13; 10; …; б) 2х; 3х + 2; … А2. Найдите четвертый член геометрической прогрессии, если b1 = 8, q = 0,5. A3. Найдите сумму 29 первых членов арифметической прогрессии (аn), если а1 = 18,7; а29 = -19,6. А4. Найдите знаменатель геометрической прогрессии -32; 64; … В1. Найдите сумму бесконечной геометрической прогрессии -40; 30; -22,5; … C1. Между числами -10 и -810 вставьте три числа так, чтобы они вместе с данными образовали геометрическую прогрессию Вариант 2 А1. Выпишите три следующих члена геометрической прогрессии: а) 4; -6; …; б) А2. Найдите 18-тый член арифметической прогрессии, если а1 =5,6, d = 0,6. A3. Найдите сумму 5 первых членов геометрической прогрессии (bn), если b1 = 5; b3 = 80. А4. Найдите разность арифметической прогрессии -12; -14; … В1. Найдите сумму всех нечетных натуральных чисел от 37 до 113 включительно. C1. Между числами -10 и -810 вставьте три числа так, чтобы они вместе с данными образовали геометрическую прогрессию Нормы оценок: «3»- любые 4А(из 5 заданий), 4» - 3А + 1В, «5» - 5А + 1В или 2А + 1В + 1С. Контрольная работа №6 по теме: «Элементы комбинаторики и теории вероятностей» Вариант 1 А1. Сколькими способами можно разместить 5 различных книг на полке? А2. Сколько трехзначных чисел, в которых нет одинаковых цифр можно составить из цифр 1, 3, 5, 7, 9? А3. В классе 20 учеников. Нужно выбрать 8 человек для участия в школьных конкурсах. Сколькими способами это можно сделать? А4. Какова вероятность того, что при бросании игрального кубика выпадет менее 2 очков? В1. Из 8 мальчиков и 5 девочек надо выделить для работы на пришкольном участке 3 мальчиков и 2 девочек. Сколькими способами это можно сделать? Вариант 2 А1. Сколькими шестизначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6 без повторения цифр? А2. Сколько четырехзначных чисел, в которых нет одинаковых цифр можно составить из цифр 1, 2, 3, 5, 7, 9? А3. В классе 15 учеников. Нужно выбрать 2 дежурных по классу. Сколькими способами это можно сделать? А4. Какова вероятность того, что при бросании игрального кубика выпадет 6 очков? В1. Из 9 ручек и 6 карандашей надо выбрать 2 ручки и 3 карандаша. Сколькими способами можно сделать этот выбор? Нормы оценок: «3»- любые 3А, 4» - 4А, «5» - 4А + 1В. Контрольная работа №7 Итоговая контрольная работа Вариант 1 А1. Решите уравнение: А2. Вычислите: 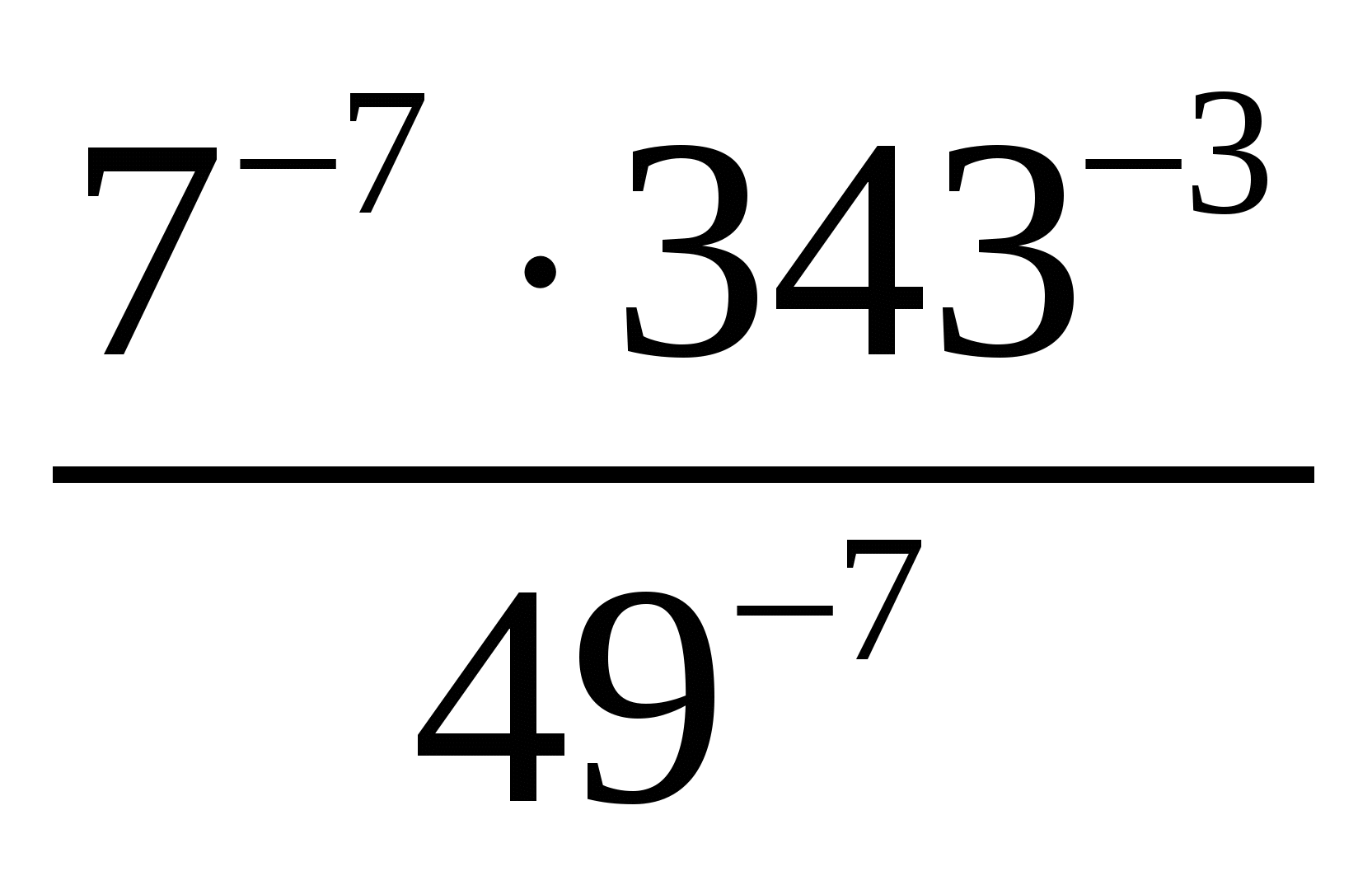 А3. Решите систему уравнений: 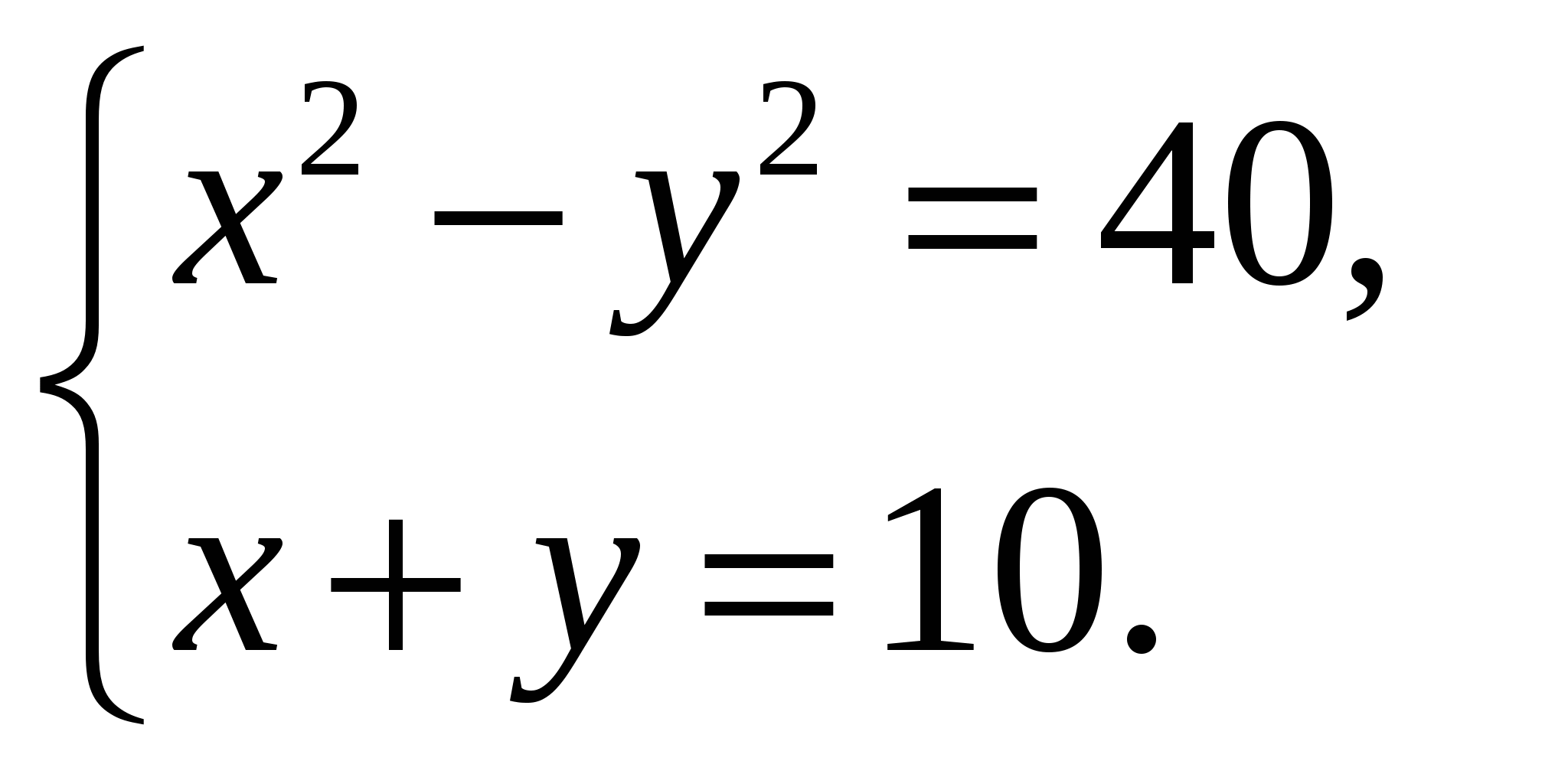 А4. Найдите область определения функции А5. Решите неравенство: 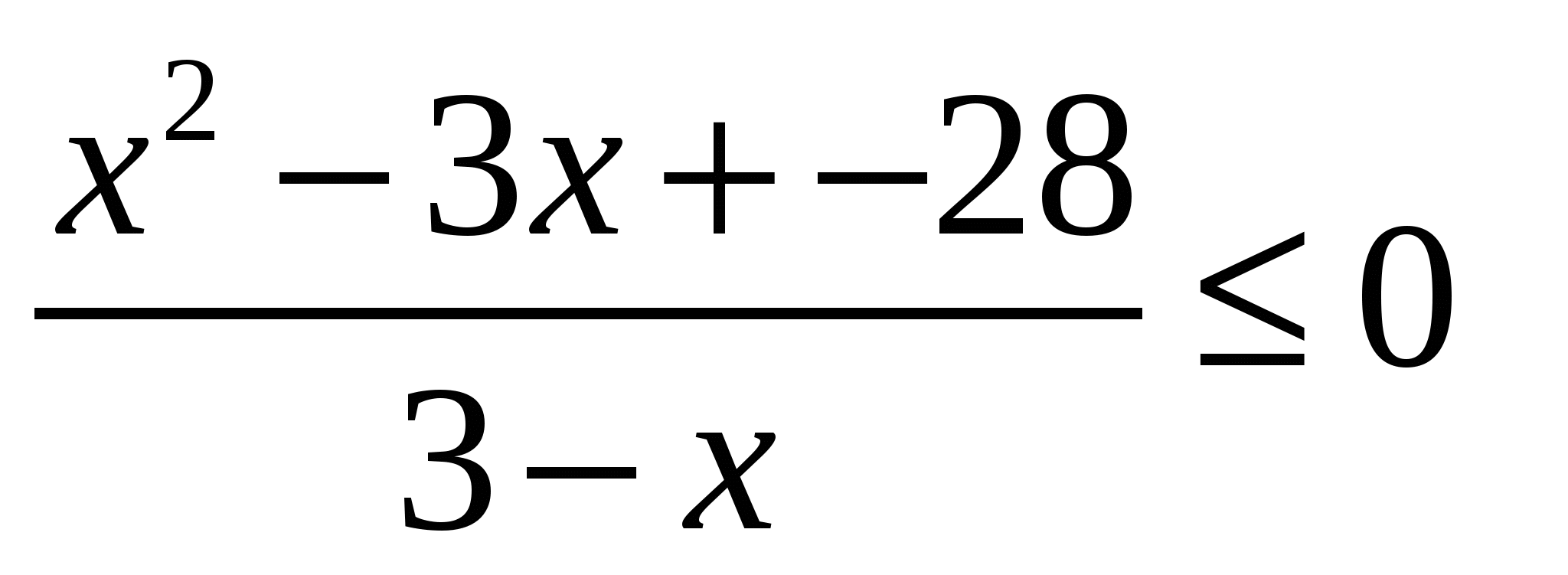 В1. Решите уравнение C1. Решите систему уравнений: 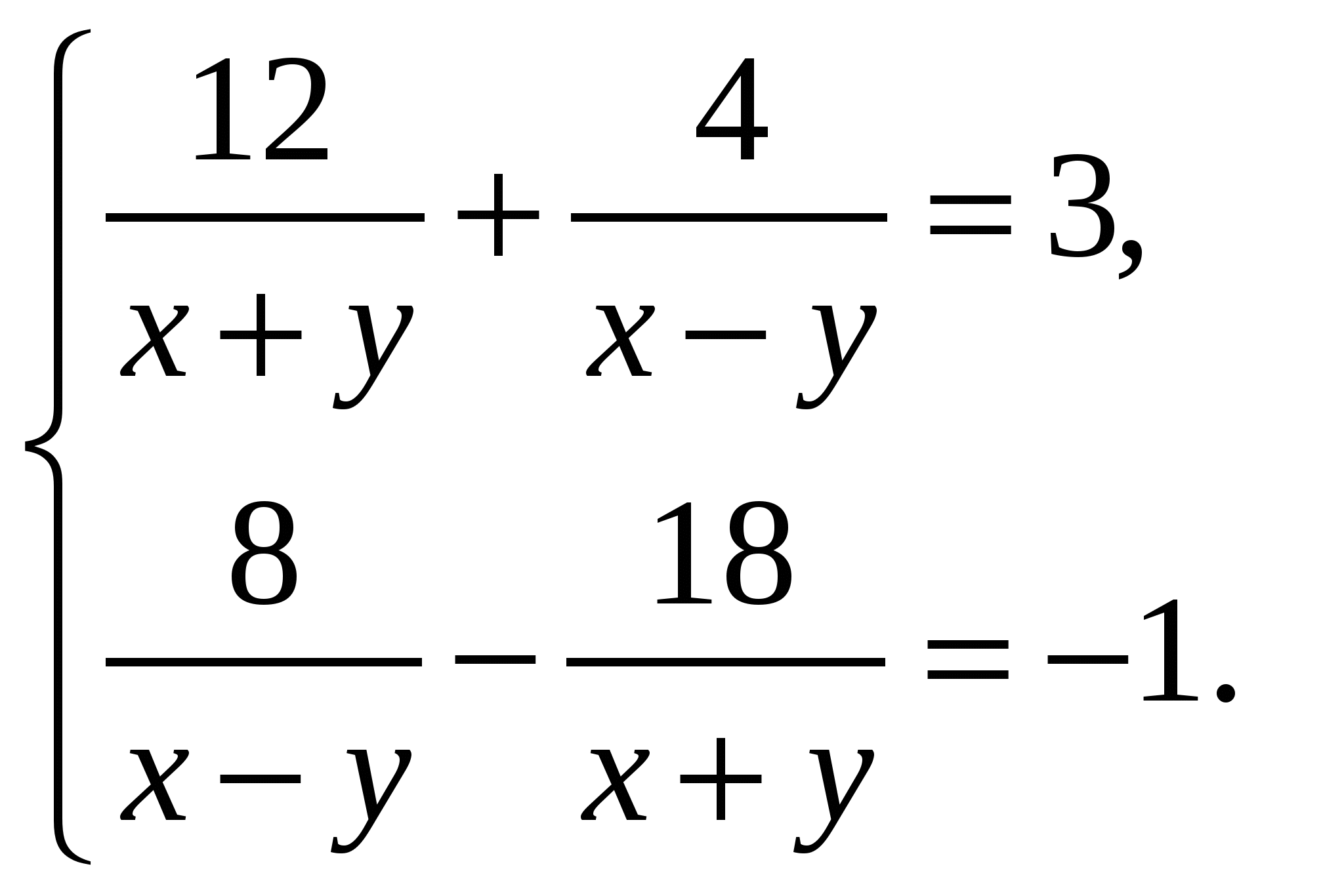 . .Вариант 2 А1. Решите уравнение: А2. Упростите выражение: 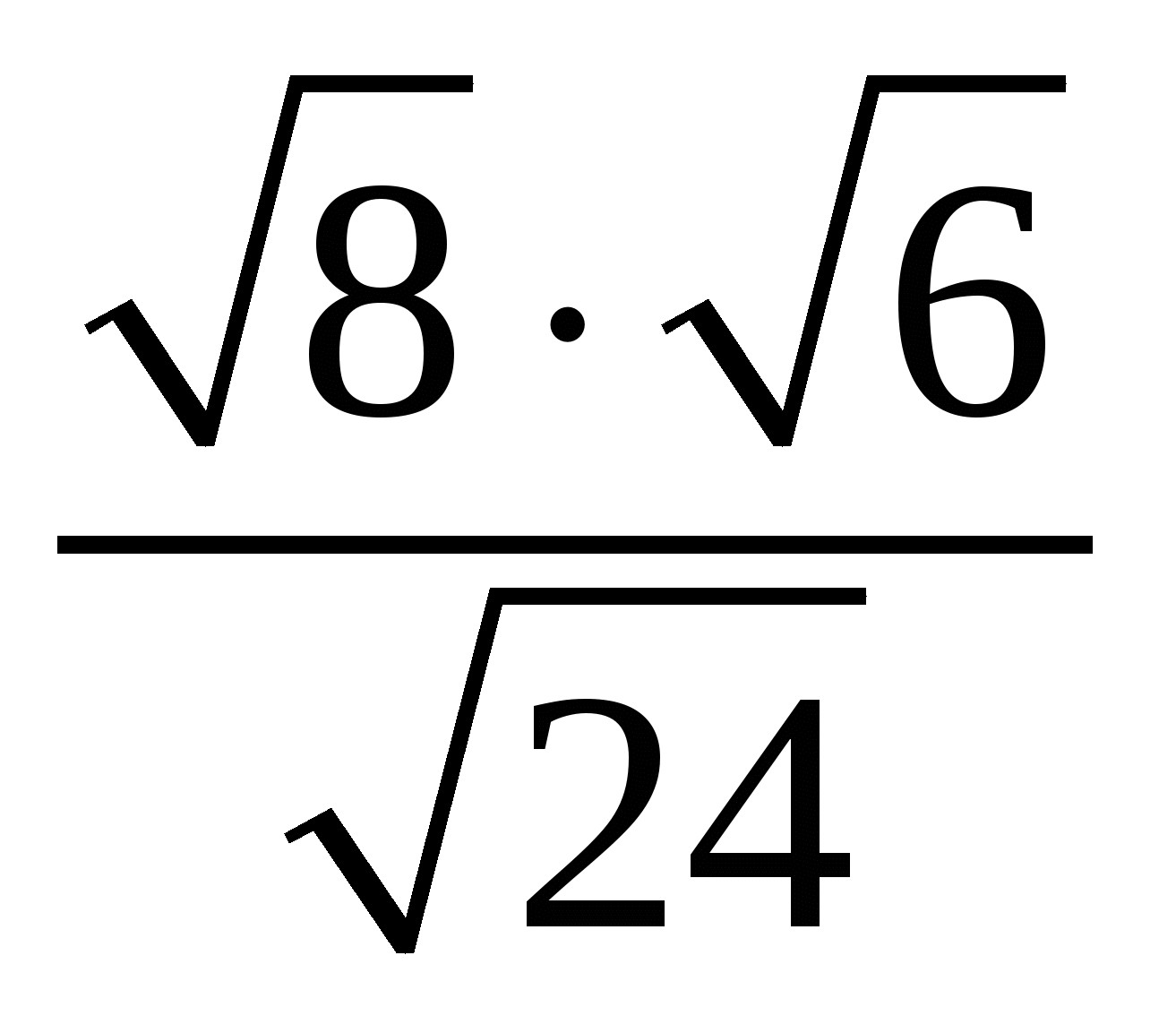 А3. Решите систему уравнений: 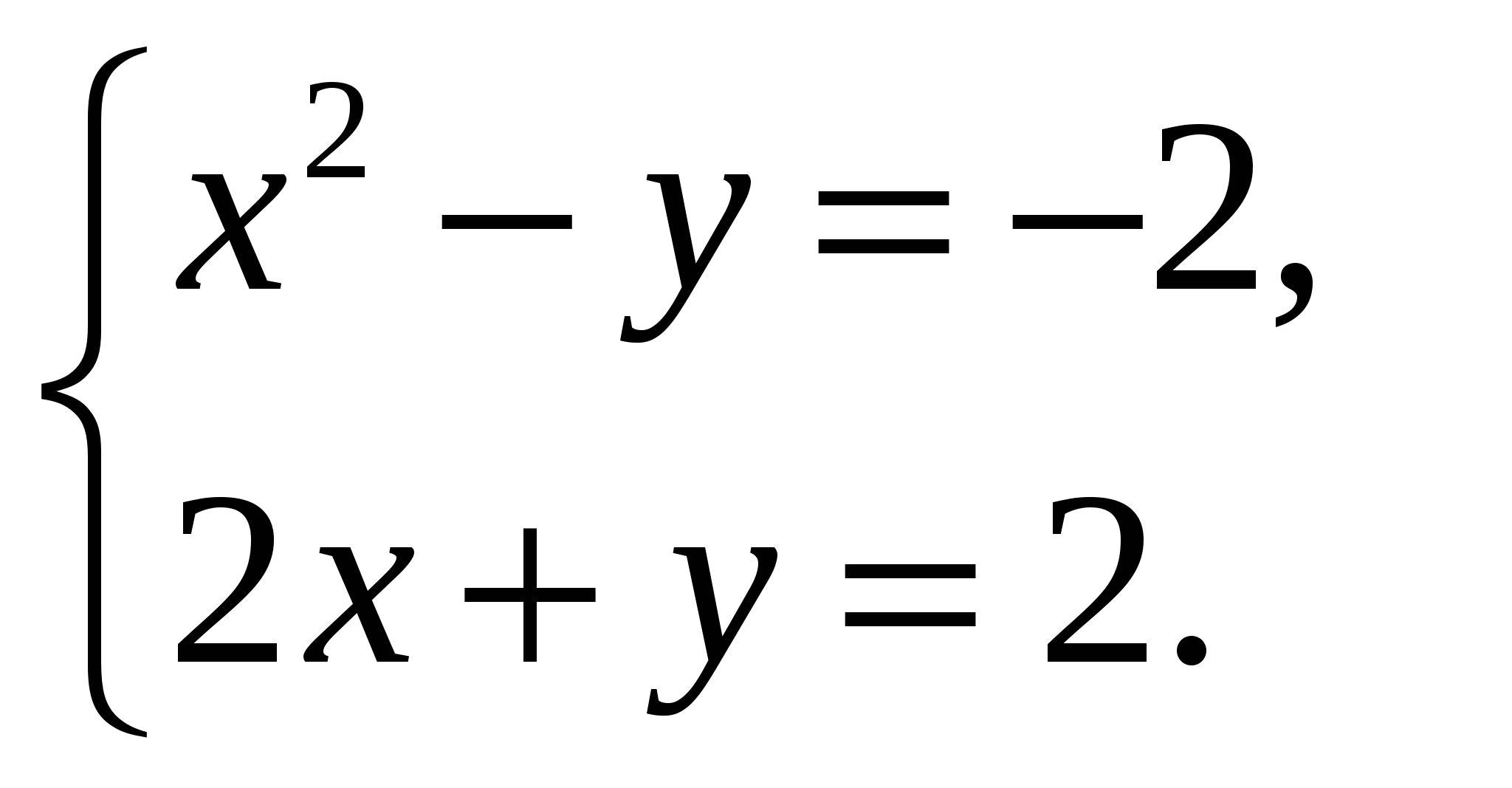 А4. Найдите область определения функции 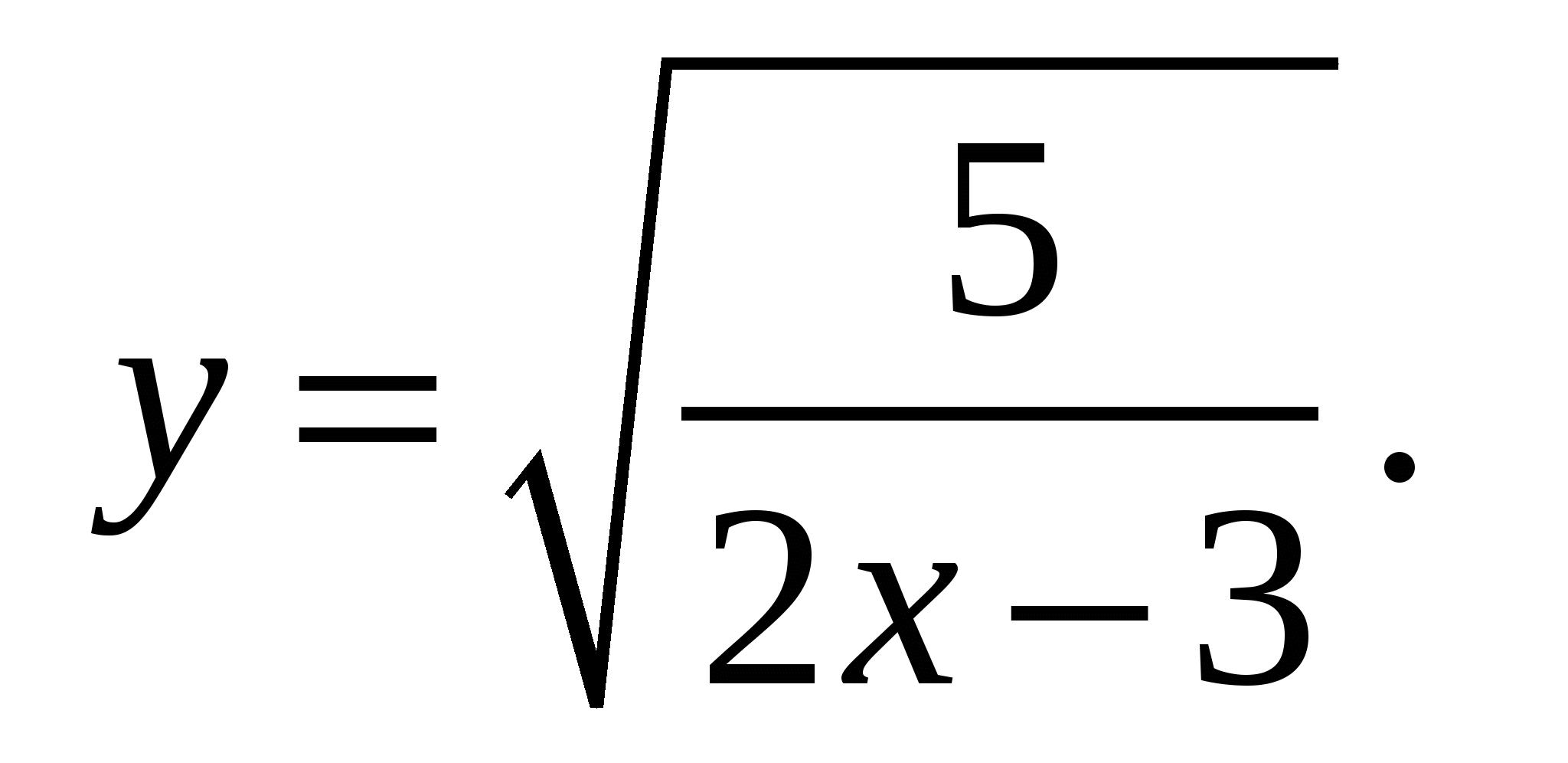 А5. Решите неравенство: В1. Решите уравнение C1. Решите систему уравнений: 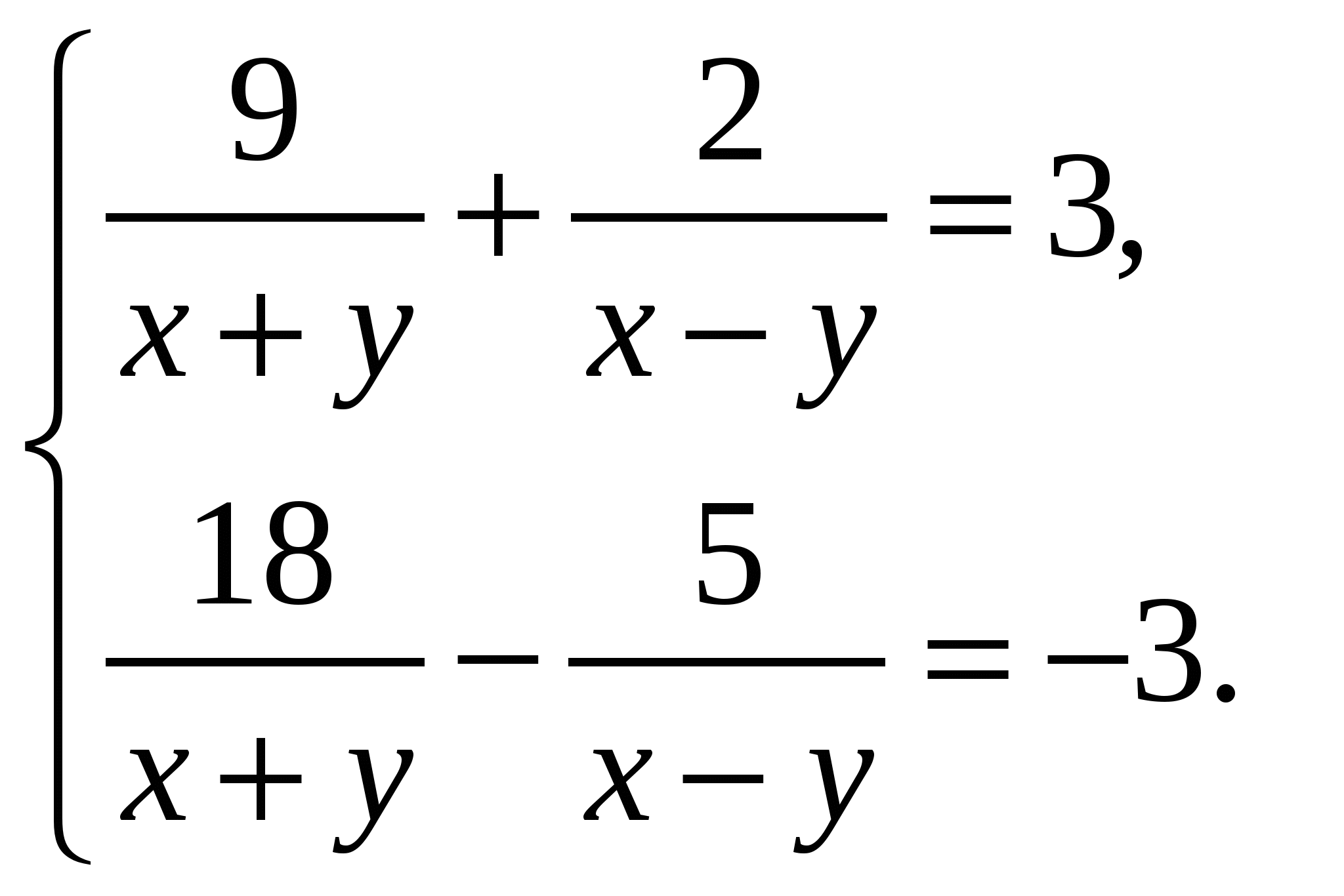 . .Нормы оценок: «3»- любые 3А, 4» - 3А + 1В, «5» - 5А + 1В или 3А + 1В + 1С. |