«Проблемное обучение на уроках и во внеурочной деятельности»
 Скачать 178.46 Kb.
|
| Использование современных образовательных технологий Тема: «Проблемное обучение на уроках и во внеурочной деятельности» Кызыл 2009 План
Дети учатся лучше и в тысячу раз успешнее, если им дают возможность самостоятельно исследовать основы изучаемого материала. Питер Клайн Актуальность темы Одним из важных направлений в психолого-педагогических исследованиях, посвященных методам обучения математике, является в настоящее время исследование сущности и приложений так называемого «проблемного обучения». Идея проблемного обучения во многом не нова. Но сравнительно недавно проблемное обучение начало проникать в практику обучения математике в средней школе. Существенным условием проявления проблемного обучения является исследовательский характер работы учащихся в процессе обучения. Сейчас уже общепризнано, что урок в школе не считается эффективным, если на этом уроке учащиеся не работают активно и самостоятельно, не решают задач, требующих не только определенных знаний, но и определенной сообразительности, догадки. Отметим, что в настоящее время проблемное обучение разрабатывается в плане его использования не только на уроках, математики, но и на уроках, посвященных изучению самых разнообразных учебных дисциплин (в частности, и дисциплин гуманитарного цикла). Можно указать на три основных способа постановки перед учащимися некоторой проблемной ситуации: а) путем четкой постановки проблемы учителем; б) путем создания ситуации, в которой от учащегося требуется самому понять и сформулировать имеющиеся в ней проблемы; в) путем создания ситуации с более или менее четко обозначенной проблемой, но по логике поиска решения которой ученик должен прийти к новой, дополнительной проблеме, им самим выявленной и предусмотренной при конструировании ситуации. Кроме того, особо выделяется такой случай в процессе обучения, когда, решая некоторую задачу, ученик самостоятельно обнаруживает новую проблему, не предусмотренную учителем при конструировании учебной ситуации. Постановка математической проблемы может осуществляться или созданием проблемной ситуации (постановка задачи с неизвестными элементами, отношениями, свойствами), или целевым заданием. Анализируя проблемную ситуацию, поставленную учителем, учащийся, как правило, должен не только найти способ решения заключенной в ней проблемы, но и привести определенное обобщение этой ситуации или сравнить с какой-либо другой ситуацией и т. д., иными словами, видеть за данной проблемой новую проблему, которую можно и целесообразно было бы изучить. Изучение нового материала в традиционном преподавании обычно сводилось к тому, что учитель сам объяснял сущность изучаемого вопроса и решал совместно с учащимися те задачи, которые закрепляли полученные только что знания. Проблемное обучение включает в себя не только постановку вводной задачи (вопроса), создание проблемной ситуации, но и самостоятельную творческую работу учащихся над данной ситуацией, открытие ими новых свойств, обоснование всех своих рассуждений. В проблемном обучении учебная ситуация, как правило, ставится перед школьниками в целостном виде, хотя некоторые ее компоненты могут сразу не проявляться (выявление этих компонентов может представлять собой специальные учебные задания). Предполагается, что разрешением поставленной перед ним проблемы учащийся занимается самостоятельно, учитель только направляет и организует работу и значительно реже «наводит на мысль». Отметим, что «проблемность» есть характеристика одной из новых форм обучения (проблемного обучения), а не характеристика метода, которым обучение осуществляется. Методом, которым осуществляется проблемное обучение, как правило, является эвристический метод, который выступает в весьма разнообразных формах, например в форме собственно эвристического метода и в форме так называемого метода «открытия», и в форме так называемого «метода активного обучения» и пр; Эвристический метод преподавания во многом отвечает тем требованиям, которые предъявляются к организации современного урока в школе с точки зрения проблемного характера обучения. Известный югославский педагог-математик С. Прванович пишет: «... учащийся получает математическое образование лишь в том случае, если учитель ведет его мысль так, чтобы он сам (в подлинном смысле этого слова) формировал математические понятия и выявлял математические факты, истины» Проблемное обучение на уроке математики Как же построить урок математики в форме проблемного обучения? Приведем примерную схему организации такого урока. 1) Создание учебной проблемной ситуации (реальной или формализованной) с целью возбудить у учащихся интерес к данной учебной проблеме и мотивировать целесообразность ее рассмотрения. 2) Постановка познавательной задачи (или задач), возникающей из данной проблемной ситуации, четкая ее формулировка. 3) Изучение различных условий, характеризующих поставленную задачу, обсуждение возможностей моделирования ее условия или замены имеющейся модели более простой и наглядной. 4) Процесс решения поставленной задачи (обсуждение задачи в целом и в деталях, выявление существенного и несущественного в ее условии; ориентация в возможных трудностях при её решении, вычленение подзадач и последовательности их решения, соотнесение данной задачи с имеющимися знаниями и опытом; разработка возможных направлений решения основной задачи; отбор, воспроизведение известных теоретических положений, могущих быть использованными в указанном направлении решения задачи, сравнительная оценка направлений решения и выбор одного из них; разработка плана решения задачи в выбранном направлении и его реализации в целом; детальная реализация плана решения задачи и обоснование правильности всех шагов возникающего решения задачи). 5) Исследование полученного решения задачи, обсуждение его результатов, выявление нового знания. 6) Применение нового знания посредством решения специально подобранных учебных задач для его усвоения. 7) Обсуждение возможных расширений и обобщений результатов решения задачи в рамках исходной проблемной ситуации. 8) Изучение полученного решения задачи и поиск других более экономичных или более изящных способов ее решения. 9) Подведение итогов проделанной работы, выявление существенного в содержании, способах решения, результатах; обсуждение возможных перспектив применения новых знания и опыта. Данный схематический план организации проблемного урока математики (как и любой другой) динамичен (в зависимости от конкретной характеристики той или иной учебной проблемы, он выполняется полностью или частично, отдельные пункты плана могут объединяться вместе и т. п.). Р 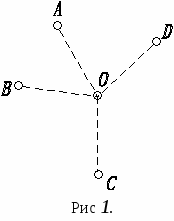 ассмотрим конкретизацию этого плана на примере краткого описания одного из уроков на тему «Вписанные четырехугольники».1) Учитель ставит перед учащимися следующую вводную задачу. «Где расположить центральный штаб игры «Зарница», чтобы он находился на равных расстояниях от заданных мест расположения четырех отрядов?» (Предлагается соответствующий рисунок.) На рисунке 1 точками А, В, С и D обозначены места расположения отрядов, а точкой О — предполагаемое место расположения штаба. 2 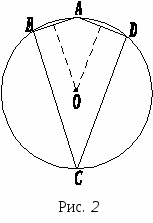 ) В процессе обсуждения этой проблемной ситуации устанавливается, что множество всех точек плоскости, удаленных от данной точки этой плоскости на данное расстояние, есть окружность, а потому в соответствии с условием задачи точки А, В, С, D принадлежат окружности, положение центра которой (точки О) неизвестно.3) Из данной проблемной ситуации возникает познавательная (и вместе с тем мыслительная) задача о возможности проведения окружности через 4 данные точки. 4) Приступив к решению задачи, учащиеся (с помощью учителя) устанавливают следующие известные им ранее факты, связанные с данной задачей: а) через одну данную точку А всегда можно провести любое число окружностей с центрами в любых (произвольно выбранных) точках; б) через две данные точки А и В можно провести бесконечное множество окружностей с центрами, расположенными на медиане отрезка АВ; в) для трех точек, не лежащих на одной прямой, существует единственная окружность, проходящая через эти три точки (теорема о вписанном треугольнике). Решение задачи сводится к отысканию условий, которым должны удовлетворять четыре точки, чтобы можно было, провести окружность, содержащую эти четыре точки. Соединив четыре данные, точки отрезками прямых, школьники получают четырехугольник ABCD, который должен быть вписанным в окружность. Начинается изучение свойств этого четырёхугольника. В ходе проводимого исследования обращается внимание на величины внутренних углов четырехугольника (рис. 2). Устанавливается, что величина угла А, как вписанного, измеряется  ; величина угла С, как вписанного, измеряется  . Следовательно, сумма величин углов А и С измеряется суммой величин дуг и , т. е. суммой Сумма величин дуг BCD и BAD равна угловой величине окружности (т. е. 4d), следовательно, сумма величин углов А и С равна 2d. Аналогично усматривается, что сумма величин углов В и D равна 2d. Выявляется, что углы А и С, В и D являются в четырехугольнике ABCD противоположными. 5) В ходе обсуждения результата решения этой задачи выявляется новое свойство вписанного четырехугольника: «Сумма величин противоположных углов вписанного четырехугольника равна 2d». Учитель отмечает, что данное утверждение представляет собой теорему, доказательство которой уже проведено в процессе решения задачи. 6) Учитель обращается к классу: «Верно ли утверждение, обратное данному? Сформулируйте, докажите или опровергните его». Учащиеся обосновывают справедливость и этой теоремы, устанавливая тем самым необходимое и достаточное условие того, чтобы любые четыре точки плоскости, из которых никакие три не лежат на одной прямой, принадлежали окружности. 7) Возвращаясь к поставленной конкретной задаче, учитель указывает на то, что остался нерешенным вопрос о том, как найти центр этой окружности. Учащиеся вспоминают, как находится центр окружности, проходящей через три заданные точки, и исследуют вопрос о том, применим ли тот же способ для нахождения центра окружности, проходящей через четыре заданные точки (будет ли четвертая точка D принадлежать окружности, центр которой нашли, используя только три точки А, В и С). Учащимся предлагается исследовать вопрос о возможных положениях точки D относительно окружности. 8) Учащимся предлагается установить, какие следствия (имеющие место для частных видов четырехугольников) можно усмотреть из этих двух теорем. (Сформулировать их.) Предлагается самостоятельно придумать задачу, где применяются изученные только что теоремы или их следствия, и объяснить ее решение. 9) Совместно с учителем изучается вопрос о том, могут ли эти теоремы оказаться полезными для решения задачи о возможности проведения окружности через 5, 6 и т. д. произвольных точек плоскости. 10) В качестве закрепления изученного учащимся предлагается самостоятельная работа следующего содержания: 1. Какая окружность называется описанной около данного четырехугольника? 2. Можно ли описать окружность около четырехугольника, величины углов которого, взятые в последовательном порядке, равны: 90°, 90°, 60°, 120°? (Ответ обосновать.) 3. Найти неизвестные величины углов вписанного в окружность четырехугольника, если известно, что величины двух его углов равны соответственно 32 и 105°. 11) Подводится общий итог работы и дается задание на дом: а) ознакомиться с изложением этой темы в учебнике; б) придумать задачу «на доказательство» (по изученной теме) и провести само доказательство; в) исследовать вопрос о том, можно ли вписать окружность в четырехугольник, каким условиям должен удовлетворять такой четырехугольник (по желанию). Понятно, что постановка уроков проблемного типа не может осуществляться повседневно прежде всего потому, что их проведение требует больших затрат учебного времени. Поэтому особенно важно отобрать тот учебный материал, который может служить основой для проблемного его изучения, не только эффективного, но и за ведомо интересного для учащихся, главное заключается здесь не в усвоении того или иного локального вопроса курса математики, а в приобщении школьников к работе творческого характера, в привитии им навыков самостоятельной работы. Приведенный выше и проиллюстрированный нами структурный план проблемного урока представляет лишь один из возможных вариантов такого урока. Проблемное обучение на уроке может осуществляться по следующему структурному плану: 1. Организация проблемной ситуации для того, чтобы: а) определить проблемы, которые потребуют у учащихся решения; б) заинтересовать учащихся проблемой, вызвать у них стремление к ее решению. 2. Ориентация в трудностях решения проблемы, выделение частных проблем и установление очередности их решения. 3. Коллективное, групповое, индивидуальное решение этих частных проблем, проверка результатов решения и исправление ошибок. 4. Объединение результатов, полученных при решении частных проблем, в решение главной проблемы. Задача первого этапа — определить проблему, требующую своего решения, и заинтересовать учащихся этой проблемой. Учебная проблема возникает либо в связи с отсутствием у учащихся определенных знаний (проблема познавательная), либо умений (проблема умений), либо в связи с отсутствием четкого отношения учащихся к познаваемому материалу (проблема оценки). Школьники осознают наличие пробелов в своих знаниях. У них появляется желание устранить эти пробелы. Такой эмоциональный момент вызывает у учащихся интерес к изучаемому материалу, концентрирует их энергию, необходимую для решения проблемы. Задача второго этапа — ознакомить учащихся с трудностями, возникающими в процессе решения проблемы. Под руководством учителя учащиеся обсуждают, что надо исследовать, что надо узнать, чтобы решить задачу. Предложения учащихся обсуждаются и классифицируются. В результате главная проблема уточняется посредством поэтапных задач — частных проблем. Учащиеся способны одновременно усвоить или открыть несколько частных проблей при условии, что эти частные проблемы логически связаны между собой. Обычно на уроке выделяется от двух до четырех частных проблем. На третьем этапе урока идет решение выделенных частных проблем. При этом возможны следующие виды работы с учащимися: а) фронтальная работа со всем классом; б) групповая работа; в) индивидуальная работа учащихся. Третий этап — это основная часть урока, и проходит она по-разному в зависимости от форм работы и способов решения проблем. Четвертый этап проблемного урока — подведение итогов решения частных проблем, их соединение и окончательное решение главной проблемы. Оно осуществляется в процессе коллективной работы, которой может предшествовать работа и групповая. Виды учебной работы школьников в условиях проблемного обучения. Групповая работа учащихся. Проблемное обучение позволяет эффективно сочетать как индивидуальную, так и групповую работу учащихся (небольшими коллективами) на уроке. В традиционном обучении групповая работа учащихся использовалась крайне: редко. Между тем групповая коллективная работа, учащихся также является эффективным способом активного приобретения ими знаний, не говоря уже о ее воспитательном значении. Как же сочетать групповую и индивидуальную работу учащихся в проблемном обучении? В примерной схеме проблемного урока основное место естественно занимает решение учебной математической проблемы. На этом этапе работа с учащимися может выступать в виде: 1) фронтальной работы со всем классом; 2) групповой работы; 3) индивидуальной работы. На выбор того или иного вида работы влияет характер работы, имеющиеся учебные средства (комплекты учебных пособий и других материалов), а также время, имеющееся в распоряжении учителя. Групповая работа предполагает деление класса на группы как примерно одинаковых (по уровню математического развития), так иногда и различных учащихся. Количественный состав группы может быть самым разнообразным. Можно указать на некоторые принципы организации групповой работы. 1. Наиболее целесообразно создавать учебные группы из 4—6 человек. 2. Состав ученических групп не следует часто менять, лучше если он является постоянным, но дифференцированным. Это способствует проявлению активности всех членов группы и ускорению темпа работы «слабых» учащихся. 3. Какой-либо из учащихся назначается руководителем группы. При этом на разных уроках работой группы руководят разные учащиеся. 4. Учебные группы ориентируются на работу примерно в одинаковом темпе, что дает возможность вести деловое обсуждение изучаемого материала. 5. Для отчета о работе всей группы учитель назначает одного из членов группы, ответ которого оценивается. Некоторые частные проблемы, входящие в данную учебную проблему, могут решаться индивидуально. При групповой работе учащихся необходимо предусмотреть и соответствующее расположение столов в классной комнате. Коллективная работа учащихся над решением какой-либо учебной проблемы никоим образом не исключает индивидуальной работы каждого из них, так как групповая работа по существу объединяет индивидуальную работу, каждого из членов коллектива. Кроме того, принцип индивидуализации обучения соблюдается посредством учета индивидуальных темпов работы каждого учащегося, уровня его знаний, возможностей и наклонностей к какому-либо виду математической деятельности (проведение рас-четов, выполнение рисунков и схем, высказывание идей и т. п.). Умелое сочетание групповой и индивидуальной формы занятий по математике обеспечивает всестороннее развитие активности и самостоятельности в обучении всех учащихся, дает возможность обсуждать изучаемую тему, оценивать результаты своих наблюдений и опыта, высказывать гипотезы. Контроль и оценка поисковой деятельности учащихся в условиях проблемного обучения. Проблемное обучение математике предусматривает строгий контроль и учет поисковой деятельности школьников, их творческой активности. Этот контроль осуществляется учителем в течение всего урока. Учитель задает вопросы по изучаемой теме классу (или группе) и тем самым контролирует работу учащихся. Контрольные вопросы могут задаваться и самими учащимися. Например, члены одной учебной группы могут задать вопросы по изучаемой теме всему классу (или другой группе). Одной из эффективных форм контроля и оценки групповой работы учащихся является их отчет. При индивидуальном решении частных проблем контроль осуществляется в самих группах или во время общей дискуссии. Учитель следит за тем, чтобы выдвинутые учащимися частные проблемы отвечали основной проблеме, являлись узловыми для ее решения, а также соответствовали очередности их рассмотрения. Оценка поисковой деятельности учащихся является стимулом для развития их познавательной активности. Возможно несколько вариантов оценки деятельности учеников. 1. Итоговая оценка за урок. 2. Оценка за решение какой-либо частной проблемы. 3. Оценка за самостоятельную работу всего коллектива. Оценку решений частной проблемы могут давать и сами учащиеся. Например, при межгрупповом обмене решений данной частной проблемы одна группа учащихся оценивает решение, данное другой группой. Но при этом учитель должен указать учащимся на основные требования к этой оценке. Сейчас в школьной практике при учете и оценке работы учащихся все более широко применяется зачетная система. Зачетную систему целесообразно применять и при проблемном обучении математике. Для проведения зачета можно составить специальные билеты из 2—3 вопросов по изучаемой теме и одной практической задачи. Формы проведения проблемных уроков. Проблемные уроки могут быть, представлены в разных формах: собственно урок, лекция, семинар, круглый стол, организационно-деятельностная игра, проектная деятельность и т.д. В заключение важно подчеркнуть значимость технологии проблемного обучения и воспитания, которая, без всяких сомнений, должна занимать одно из ведущих мест в педагогической деятельности. Во-первых, с точки зрения ценностного подхода, данную технологию следует охарактеризовать как:
Сказанное можно продемонстрировать при помощи матрицы соответствия технологии проблемного обучения и воспитания проявлениям трех вышеназванных ценностей образования. Матрица соответствия технологии проблемного обучения и воспитания
Во-вторых, данная технология активно «взаимодействует» со всеми основными образовательными технологиями:
Кстати, активно применяемая в последнее время технология проектной деятельности, как мне представляется, является разновидностью технологии проблемной деятельности. Ожидаемые результаты
Список использованной литературы
|