|
Пояснительная записка Планирование учебного материала Тематические тестовые работы
Методические рекомендации
к проведению итогового повторения в 9 классе за курс алгебры 7-9-х классов.
Содержание
1. Пояснительная записка
Планирование учебного материала
Тематические тестовые работы
Обобщающая тестовая работа
Пояснительная записка
В 9 -ом классе, дети начинают чувствовать тревожность перед экзаменами, пытаются как-то готовиться к ним, но самостоятельно повторять и систематизировать весь материал, пройденный в 7-9 классах, не каждому выпускнику под силу. На занятиях итогового повторения есть возможность устранить пробелы ученика по тем или иным темам. Ученик более осознанно подходит к материалу, который изучался в 7-9 классах, т.к. у него уже более большой опыт и богаче багаж знаний. Учитель помогает выявить слабые места ученика, оказывает помощь при систематизации материала, готовит правильно работать с контрольно – измерительными материалами.
Особенность принятого подхода итогового повторения состоит в том, что для занятий по математике предлагаются небольшие фрагменты, рассчитанные на 2-3 урока, относящиеся к различным разделам школьной математики.
Каждое занятие, а также все они в целом направлены на то, чтобы развить интерес школьников к предмету, познакомить их с новыми идеями и методами, расширить представление об изучаемом в основном курсе материале, а главное, порешать интересные задачи.
Если в изучении предметов естественнонаучного цикла очень важное место занимает эксперимент и именно в процессе эксперимента и обсуждения его организации и результатов формируются и развиваются интересы ученика к данному предмету, то в математике эквивалентом эксперимента является решение задач. Собственно вся итоговая подготовка по алгебре строится как правило на решении различных по степени важности и трудности задач. После каждого раздела проверочная тестовая работа.
В ходе итогового повторения необходимо оказать индивидуальную и систематическую помощь ученикам . Для этого необходимо выявить уровень усвоения знаний учащихся по отдельным темам, поэтому после каждого раздела проверочная тестовая работа.
Затем необходимо спланировать оставшееся время по устранению пробелов в знаниях отдельных категорий учащихся, так и продвижению более успешных выпускников.
Итоговое повторение учебного материала стоит проводить, используя блочно – модульное структурирование учебного материала, расставляя акценты на « западающие» модули. Выстраивать повторение необходимо от простых заданий ( типовых ) до заданий повышенного и высокого уровня сложности.
Полезно учить школьников использовать различные « хитрости» для получения ответа наиболее простым и быстрым способом, требовать самоконтроля полученных результатов.
Стоит искать оптимальные подходы к организации работы обучающихся. Подробный разбор отдельных заданий полезно сочетать с алгоритмом решения других задач, рассмотрением разных подходов к решению одной задачи.
Тренировочные тесты необходимо проводить с жестким ограничением во времени.
Домашние задания должны обязательно включать упражнения разного уровня сложности.
Конечно, можно продолжить перечень различных ресурсов для качественной подготовки учащихся к итоговой аттестации.
Однако главной задачей учителя становится создание условий, мотивирующих выпускника к успешной сдачи экзаменов.
Примерное планирование учебного времени
( итоговое повторение)
№ п/п
|
Наименование темы
|
Коли
чество часов
|
дата
|
Примечание
|
1
|
Числа и вычисления
|
1
|
04.04.14
|
Тестовая работа на 20 минут
|
2
|
Числа и вычисления
|
1
|
06.04.14
|
|
3
|
Алгебраические выражения
|
1
|
07.04.14
|
|
4
|
Алгебраические выражения
|
1
|
11.04.14
|
Тест № 2
(30 мин)
|
5
|
Уравнения и системы уравнений
|
1
|
13.04.14
|
|
6
|
Уравнения и системы уравнений
|
1
|
14.04.14
|
|
7
|
Уравнения и системы уравнений
|
1
|
18.04.14
|
|
8
|
Тест № 3 по теме «Уравнения и системы уравнений»
|
1
|
20.04.14
|
|
9
|
Неравенства, системы неравенств
|
1
|
21.04.14
|
|
10
|
Неравенства, системы неравенств
|
1
|
25.04.14
|
|
11
|
Неравенства, системы неравенств
|
1
|
27.04.14
|
|
12
|
Неравенства, системы неравенств
|
1
|
28.04.14
|
Тест № 4
(30 мин)
|
13
|
Последовательности и прогрессии
|
1
|
04.05.14
|
|
14
|
Последовательности и прогрессии
|
1
|
05.05.14
|
|
15
|
Последовательности и прогрессии
|
1
|
11.05.14
|
Тест № 5
(30 мин)
|
16
|
Функции
|
1
|
12.05.14
|
|
17
|
Функции
|
1
|
16.05.14
|
|
18
|
Тест № 6 по теме «Функции»
|
1
|
18.05.14
|
|
19
|
Урок - консультация
|
1
|
19.05.14
|
|
20-21
|
Обобщающая тестовая работа
|
2
|
16.05.14
|
Демонстрационный вариант
|
Числа и вычисления
Тест № 1
Из чисел 1, 130 ∙ 106; 5, 713 ∙ 105; 4, 011 ∙ 106; 2, 315 ∙ 106 выберите наибольшее
1, 130 ∙ 106; 2) 5, 713 ∙ 105; 3) 4, 011 ∙ 106; 4) 2, 315 ∙ 106
Коллекция состоит из почтовых марок «Флора» и почтовых марок «Фауна», собранных в отношении 4 : 5. Какой примерно процент в этой коллекции составляют почтовые марки «Фауна»?
80% 2) 0, 56% 3) 56% 4) 44%
На координатной прямой отмечены точки F, E, K, P. (см. рис.) Одна из них соответствует числу 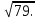 Какая это точка? Какая это точка?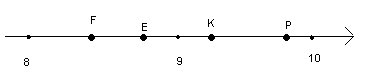
Точка F; 2) точка Е; 3) точка К; 4) точка Р
В таблице даны результаты забега мльчиков 9 класса на дистанцию 200 метров. Зачет выставляется при условии, что показан результат не хуже 35, 4с.
Номер дорожки
|
I
|
II
|
III
|
IV
|
Время (с)
|
35, 5
|
35, 3
|
35, 8
|
34, 9
|
Укажите номер дорожек, по которым бежали мальчики, получившие зачет.
I, II 2) только II 3) только III 4) II, IV
Какому из данных промежутков принадлежит числло 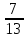 ? ?
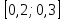 2) 2)  3) 3) 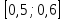 4) 4) 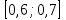
Каждое из чисел соотнесите с соответствующей ему точкой координатной прямой.

-
Ответ:
-
В социологическом опросе приняли участие 3 000 человек, из которых 563 – учащиеся. Сколько приблизительно процентов от общего количества опрошенных составляют учащиеся.
53% 2) 19% 3) 5,3% 4) 1,9%
Числа а и в отмечены точками на числовой оси. Расположите в порядке возрастание числа -  ; - ; - 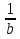 ; и – 1. ; и – 1.
– 1; -  ; - ; - 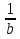 2) – 1; - 2) – 1; - 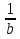 ; - ; -  3) - 3) - 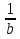 ; - 1; - ; - 1; -  ; 4) - ; 4) -  ; - 1; - ; - 1; - 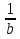

Запишите число 0, 0058 в стандартном виде.
5.8 ∙ 10- 6; 2) 5.8 ∙ 10- 5; 3) 5.8 ∙ 10- 4; 4) 5.8 ∙ 10- 3
Алгебраические выражения
Тест № 2
Найдите значение выражения 1,1x2 – 2 – 0.9x3 при х = - 1.
0 2) – 2,2 3) – 1,8 4) – 4
Какое из выражений не имеет смысла при х = - 2 и х = 3.
 2) 2) 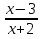 3) 3)  4) 4) 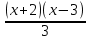
Из формулы S = 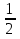 a ∙ b sin j выразите sin j. a ∙ b sin j выразите sin j.
sin j = 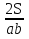 2) sin j = 2) sin j = 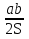 3) sin j = 3) sin j = 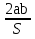 4) sin j = 4) sin j = 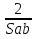
Какое из приведенных ниже выражений тождественно равно произведению (4 – х) (х – 6)?
(4 – x)(6 – x) 2) (x – 4)(x – 6) 3) - (x – 4)(x – 6) 4) – (x – 4)(6 – x)
Упростите выражение a - 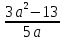 . .
 2) 2) 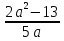 3) 3)  4) 4) 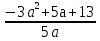
Какое из выражений не равно выражению  ? ?
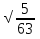 2) 2) 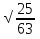 3) 3) 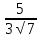 4) 4)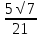
Длина шага человека x см. По какой формуле можно вычислить число шагов n, которые ему надо сделать, чтобы пройти S метров?
n = 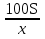 2) n = 2) n = 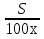 3) n = 3) n =  4) n = 100Sx 4) n = 100Sx
Найдите значение выражения a2 + 4a – 7 при a = 5 - 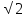
Решение:
Найдите область определения выражения 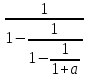
Решение:
Уравнения, системы уравнений
Тест № 3
Какое из чисел является корнем уравнения: x3 – 6x2 + 13x – 20 = 0
0 2) 1 3) – 1 4) 4
Решите уравнение: 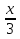 + + 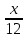 = - 5 = - 5
Ответ:
Для каждого уравнения из первой строки укажите множество его корней во второй строке.
А) 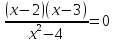 Б) Б) 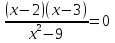 В) В) 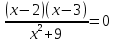
1) x = 2 2) x = 3 3) x1 = 2; x2 = 3
Вычислите координаты точек пересечения параболы у = х2 – 10 и прямой у = 4х + 11.
(39; 7) и ( -1; - 3) 2) (7; - 3) и (39; - 1)
3)( - 3; 7) и ( - 1; 39) 4) (7; 39) и ( - 3; - 1)
Прочитайте задачу: Сторона треугольника на 10 см больше высоты, опущенной на нее, а его площадь равна 40 см2. Найдите длину данной высоты. Составьте уравнение по условию задачи, обозначив длину искомой высоты за х.
Ответ:
Для каждой системы уравнений укажите соответствующие утверждения.
А) 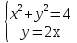 Б) Б) 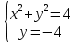 В) В) 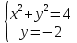
1) система не имеет решений.
2) система имеет одно решение.
3) система имеет два решения.
Ответ:
-
Решите уравнение х2 + 5х – 24 = 0. В ответ запишите произведение корней.
Ответ:
Первоначально футболка стоила 320 рублей. На распродаже ее цена снизилась на 15 %. Сколько стала стоить футболка после скидки?
Решите уравнение: (х2 – 3х)(х2 – 3х – 2) = 8
Вычислите координаты точек пересечения параболы у = х2 + 2х – 1 и гиперболы у = 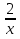 . .
Неравенства, системы неравенств
Тест № 4
Решите неравенство: 5х – 2(х – 4)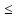 9х + 20 9х + 20
x ≤ 2 2) x ≥ 2 3) x ≤ - 2 4) x ≥ - 2
О числах a, b и c известно, что a > b > c. Какое из следующих чисел отрицательно?
a – b 2) b – c 3) a – c 4) c – b
На рисунке изображен график функции y = - x2 + 4x – 3. Используя рисунок, решите неравенство х2< 4х – 3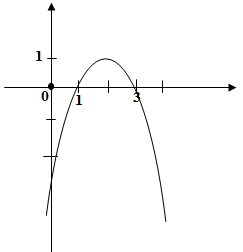
Какое из следующих неравенств не следует из неравенства х > y – z?
x + z > y 2) y < x + z 3) x – y + z > 0 4) y - z – x > 0
Укажите неравенство, решением которого является любое число.
x2 + 9 < 0 2) x2 – 9 < 0 3) x2 + 9 > 0 4) x2 – 9 > 0
Для каждой системы неравенств укажите номер рисунка, на котором изображено множество ее решений.
 
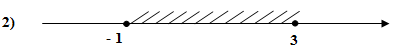
Б) 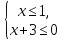 
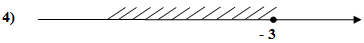
В) 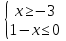
Ответ:
-
Найдите область определения выражения: 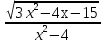
Решите неравенство: 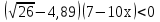
При каких значениях p система неравенств имеет значение?
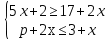
Последовательности и прогрессии
Тест № 5
Последовательность задана формулой an = ( - 1)n ∙n. Какое из следующих чисел не является членом этой последовательности?
2 2) 4 3) 5 4) 8
Последовательности заданы несколькими первыми членами. Одна из них – арифметическая прогрессия. Укажите ее.
1; 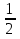 ; ; 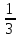 ; ; 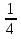 ; … 3) 1; 3; 5; 7; … ; … 3) 1; 3; 5; 7; …
1; 2; 4; 8; … 4) 1; 2; 3; 5; …
Записаны несколько последовательных членов геометрической прогрессии. Найдите член прогрессии, обозначенный буквой х.
…; 14; х; 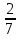 ; ; 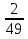 ; … ; …
Ответ:
Из арифметических прогрессий, заданных формулой n – го члена, выберите ту, для которой выполняется условие a40> 0
an = - 9n + 400 2) an = 9n – 400 3) an = 9n – 360 4) an = - 9n
Для каждой арифметической прогрессии, заданной формулой n – го члена, укажите ее разность d.
А) an = 4n + 3 Б) bn = 2n + 4 В) cn = 3n – 2
1) d = - 2 2) d = 4 3) d = 2 4) d = 3
Ответ:
-
Геометрическая прогрессия задана условиями: b1 = 2, bn+1 = 3 ∙ bn. Укажите формулу n – го члена этой прогрессии.
bn = 3 ∙ 2n-1 2) bn = 3 ∙ 2n 3) bn = 2 ∙ 3n-1 4) bn = 2 ∙ 3n
Начиная с какого номера члены арифметической прогрессии 8; 11; 14; … больше 150?
a48 2) a49 3) a51 4) a52
Сколько положительных членов в последовательности (Сn), заданной формулой Cn = 47 – 5n
9 2) 8 3) 10 4) 7
Арифметическая прогрессия задана формулой n – го члена an = 3n + 5. Найдите сумму членов арифметической прогрессии с 30 – го по 40 – й включительно.
1211 2) 1210 3) 1200 4) 1220
Функция
Тест № 6
Найдите значение функции y = 20x3 + 8x2 – 1 при значении аргумента, равном 0,1.
0 2) – 0,72 3) – 0,9 4) – 0,18
Найдите область определения функции y = 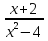
( - ∞; 2)  ( 2; + ∞) 3) ( - ∞; - 2) ( 2; + ∞) 3) ( - ∞; - 2)  (- 2; 2) (- 2; 2)  ( 2; + ∞) ( 2; + ∞)
( - ∞; - 2)  (- 2; + ∞) 4) ( - ∞; + ∞) (- 2; + ∞) 4) ( - ∞; + ∞)
График какой из перечисленных ниже функций изображен на рисунке?
y = x2 + 4 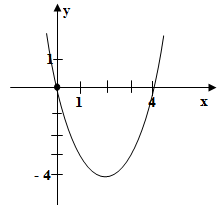
y = x2 + 4x
y = x2 – 4
y = x2 – 4x
Функции заданы формулами.
А) y = 5x + 1 Б) x = 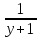 В) y = x2 – 2x Г) y = x3 – 3x2 + 3x В) y = x2 – 2x Г) y = x3 – 3x2 + 3x
Найдите в этом перечне функции, графики которых проходят через начало координат.
В, Г 2) А, Б 3) А, Г 4) В, А
Какая из данных парабол имеет с гиперболой y =  три общие точки? три общие точки?
y = - x2 2) y = x2 + 100 3) y = x2 – 1 4) y = x2 – 100
На рисунке изображен график функции y = kx + b. Определите знаки коэфициентов k и b.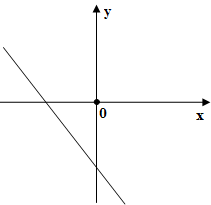
k > 0, b > 0
k > 0 , b < 0
k < 0, b > 0
k < 0, b < 0
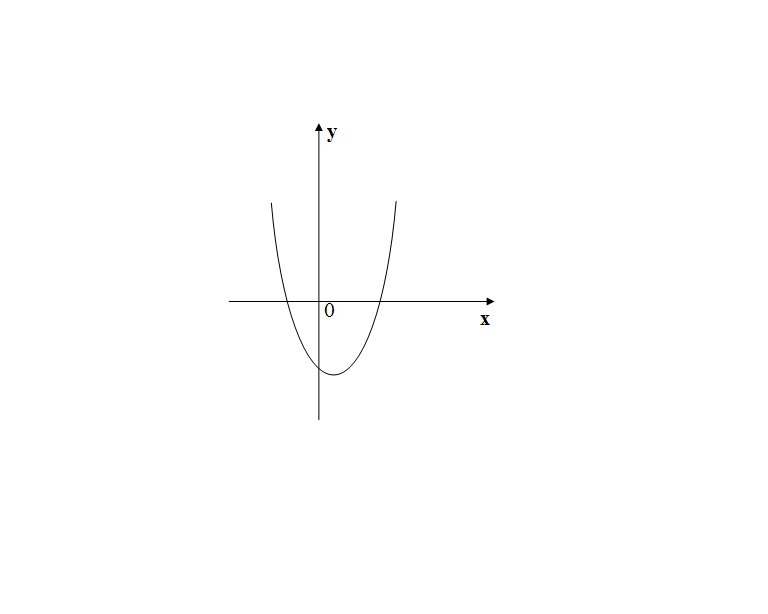
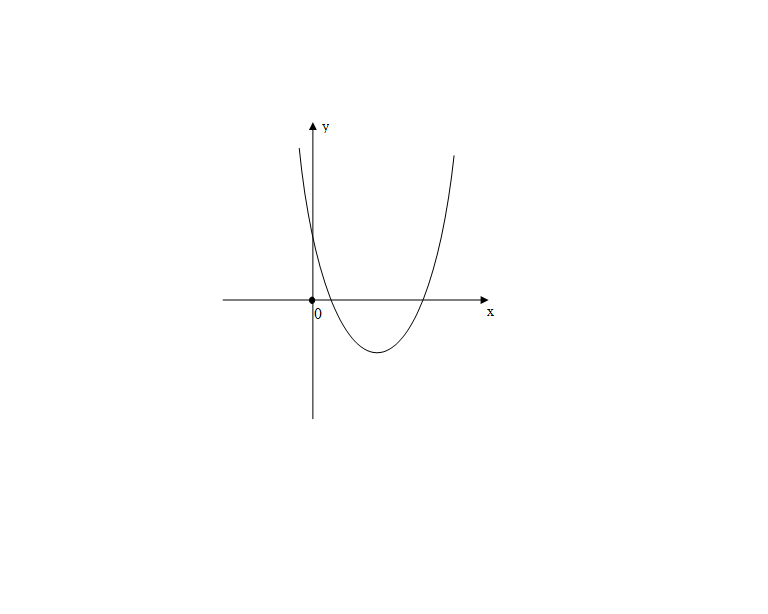
Дана функция y = ax2 + bx + c. На каком рисунке изображен график этой функции, если известно, что a > 0 и квадратный трехчлен ax2 + bx + c имеет два положительных корня?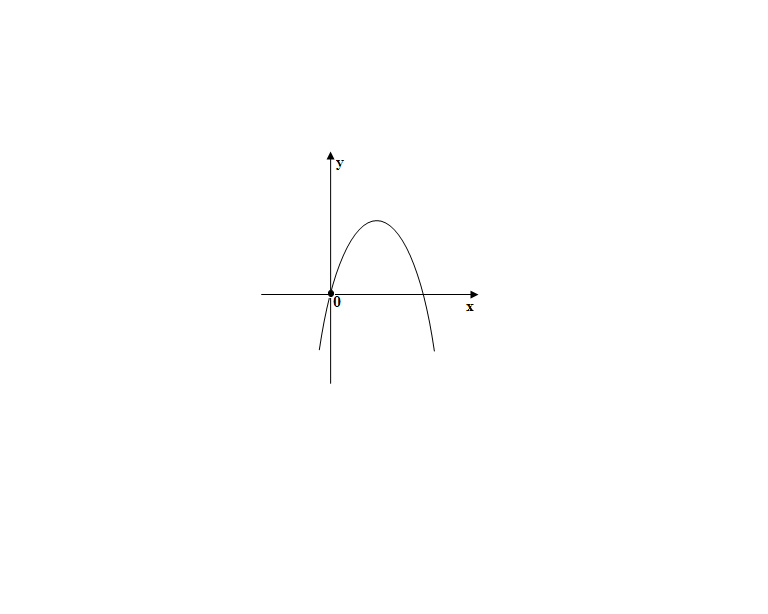
2)
 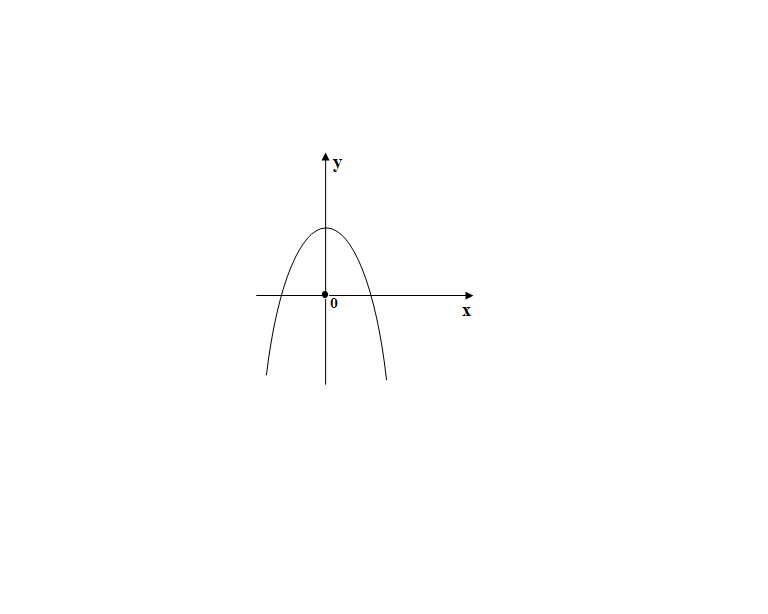
3)
4)
На рисунке изображен график функции y =f(x), областью определения которой является промежуток [ - 4; 4]. Используя рисунок, выясните, какое из утверждений неверно.
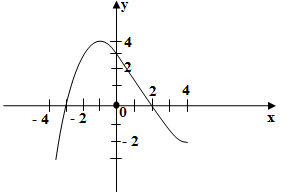
Если x = - 2, то f(x) = 3.
f (- 3) < f (3).
Наибольшее значение функции равно 4.
Функция возрастает на промежуток [ - 4; - 1].
Найдите множество значений функции: f(x) = - x2 – 4x + 5
( - ∞; + ∞) 2) ( - ∞; 9] 3) [ - 7; + ∞) 4) ( - ∞; 9)
Найдите значение d, при котором график функции f(x) = 3x2 – 6x + d имеет одну общую точку с осью абцисс.
3 2) – 3 3) 3; - 3 4) 0
Графиком квадратной функции служит парабола с вершиной в начале координат и проходящая через точку В ( - 1; 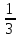 ). Задайте эту функцию формулой. ). Задайте эту функцию формулой.
y = - 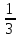 x2 2) y = x2 2) y = 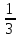 x2 3) y = 3x2 4) y = - 3x2 x2 3) y = 3x2 4) y = - 3x2
ОТВЕТЫ
Тест № 1 Числа и вычисления
№ п/п
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
ответ
|
3
|
3
|
2
|
4
|
3
|
341
|
2
|
4
|
4
|
Тест № 2 Алгебраические выражения
№ п/п
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
ответ
|
1
|
3
|
1
|
3
|
3
|
1
|
1
|
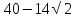
|
a ≠ 0
a ≠ 1
|
Тест № 3 Уравнения, системы уравнений
№ п/п
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
ответ
|
4
|
- 12
|
213
|
4
|
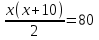
|
312
|
- 24
|
272
|
-1; 1;2;4.
|
Тест № 4 Неравенства, системы неравенств
№ п/п
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
ответ
|
4
|
4
|
(1;3 )
|
4
|
3
|
243
|
(-∞;-2)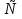 (-2;- (-2;- ] ]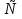 [3;+∞) [3;+∞)
|
(0,7; + ∞)
|
р ≤ -3
|
Тест № 5 Последовательности и прогрессии
№ п/п
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
ответ
|
3
|
3
|
2
|
1
|
234
|
3
|
2
|
1
|
2
|
Тест № 6 Функция
№ п/п
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
ответ
|
3
|
3
|
4
|
1
|
3
|
4
|
4
|
2
|
2
|
1
|
2
| |
|
|
 Скачать 188.27 Kb.
Скачать 188.27 Kb.

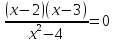 Б)
Б) 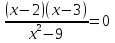 В)
В) 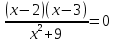
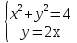 Б)
Б) 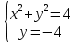 В)
В) 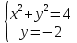
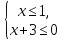
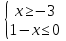
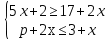
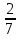 ;
; 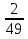 ; …
; … 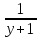 В) y = x2 – 2x Г) y = x3 – 3x2 + 3x
В) y = x2 – 2x Г) y = x3 – 3x2 + 3x

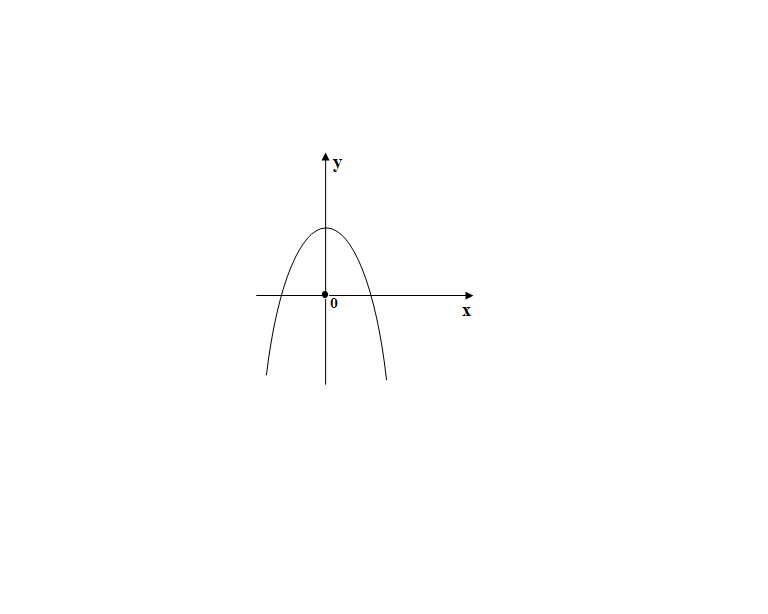
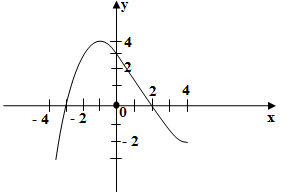
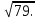 Какая это точка?
Какая это точка?
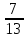 ?
?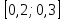 2)
2)  3)
3) 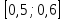 4)
4) 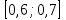
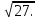

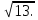
 ; -
; - 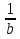 ; и – 1.
; и – 1. 2)
2) 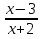 3)
3)  4)
4) 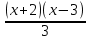
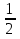 a ∙ b sin j выразите sin j.
a ∙ b sin j выразите sin j.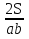 2) sin j =
2) sin j = 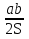 3) sin j =
3) sin j = 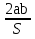 4) sin j =
4) sin j = 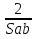
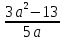 .
. 2)
2) 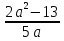 3)
3)  4)
4) 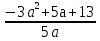
 ?
?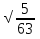 2)
2) 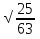 3)
3) 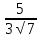 4)
4)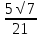
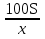 2) n =
2) n = 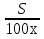 3) n =
3) n =  4) n = 100Sx
4) n = 100Sx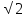
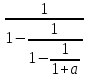
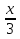 +
+ 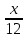 = - 5
= - 5 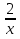 .
.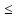 9х + 20
9х + 20

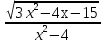
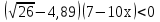
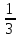 ;
; 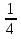 ; … 3) 1; 3; 5; 7; …
; … 3) 1; 3; 5; 7; …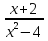
 ( 2; + ∞) 3) ( - ∞; - 2)
( 2; + ∞) 3) ( - ∞; - 2) 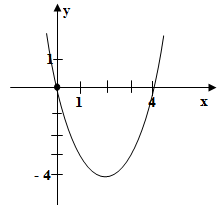
 три общие точки?
три общие точки?
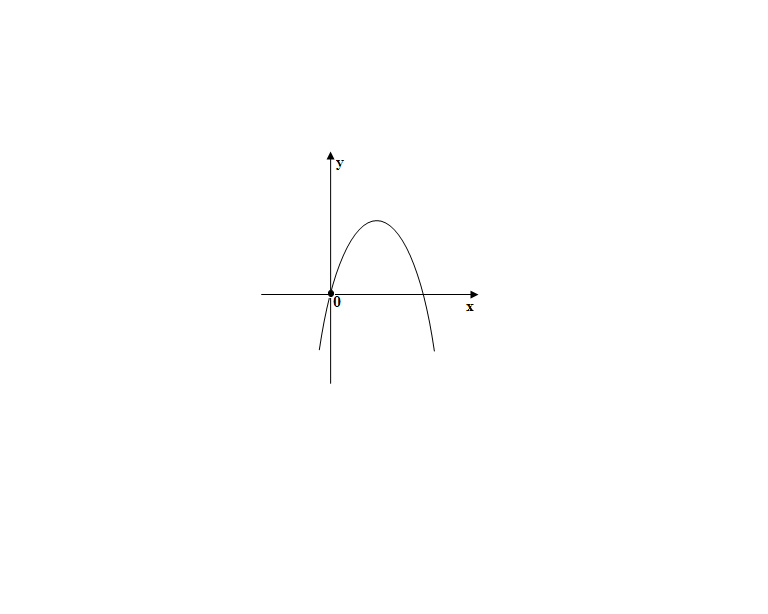
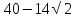
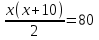
 ]
]