|
Пояснительная записка. Изучение алгебры в 10 классе на базовом уровне направлено на достижение следующих
Пояснительная записка.
Изучение алгебры в 10 классе на базовом уровне направлено на достижение следующих целей:
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики; развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для получения образования в областях, не требующих углубленной математической подготовки;
воспитание средствами математики культуры личности: отношения к математике как части общечеловеческой культуры: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.
Календарно-тематическое планирование составлено на основе нормативных документов:
Федеральный компонент государственного образовательного стандарта начального общего, основного общего и среднего (полного) общего образования - М.: Дрофа, 2004
Примерной программы основного общего образования и авторской программы линии И.И. Зубаревой, А. Г. Мордковича.
Федеральный базисный учебный план для среднего (полного) общего образования.
Место предмета в базисном учебном плане
Согласно Федеральному базисному учебному плану на изучение алгебры и начала анализа отводится 102 часа, из расчета 3 ч в неделю. В том числе контрольных работ-6 часов. Используется учебник Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (базовый уровень)/А.Г. Мордкович. – 11-е изд., стер. – М. : Мнемозина, 2010.
Формой промежуточной и итоговой аттестации являются:
контрольная работа;
самостоятельная работа;
С учетом возрастных особенностей учащихся 10 класса выстроена система учебных занятий, спроектированы цели, задачи, продуманы возможные формы контроля, сформулированы ожидаемые результаты обучения.
Учебный план
Разделы программы
|
Всего часов
|
Контрольная работа
|
Самостоятельная работа
|
Глава 1. Числовые функции.
|
5
|
-
|
|
Глава 2. Тригонометрические функции.
|
28
|
3
|
|
Глава 3. Тригонометрические уравнения.
|
15
|
1
|
|
Глава 4. Преобразование тригонометрических выражений.
|
14
|
1
|
|
Глава 5. Производная.
|
33
|
3
|
|
Повторение. Итоговая контрольная работа
|
6
|
1
|
|
Итого:
|
102
|
9
|
|
|
|
|
|
Учебно – тематический план
|
№ уч. нед. в теч. года
(дата)
|
Поурочное планирование
|
Ученик должен знать (основные понятия, термины)
|
Ученик должен уметь
(предметные умения)
|
Ключевые понятия, которые необходимо повторить
|
№ урока
|
Тема
|
|
|
Глава 1. Числовые функции
|
|
1
2
|
§ 1. Определение числовой функции и способы ее задания
|
|
|
функция
|
|
3
4
|
§2. Свойства функций
|
|
|
Свойства функций
|
|
5
|
§3. Обратные функции
|
|
|
Функция, область определения
|
|
|
Глава 2. Тригонометрические функции
|
|
6
7
|
§ 4. Числовая окружность
|
понятие числовой окружности.
|
записывать множество чисел, соответствующих на числовой окружности точке, находить на числовой окружности точку, соответствующую данному числу
|
окружность
|
|
8
9
10
|
§5. Числовая окружность на координатной плоскости
|
числовая окружность на координатной плоскости, таблица значений
|
находить на числовой окружности точки с конкретным значением абсциссы и ординаты, а также определять каким числам они соответствуют.
|
Окружность, система координат, координатная плоскость
|
|
11
|
Контрольная работа №1
|
проверить теоретические и практические знания по теме: «Числовая окружность».
|
|
12
13
14
|
§6. Синус и косинус, тангенс и котангенс
|
понятие синуса и косинуса, тангенса и котангенса, их свойств, таблица их значений, решение уравнений и неравенств вида 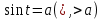 и и 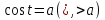 , формулы , формулы  и и 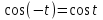
|
использовать свойства тригонометрических функций.
|
Геометрические определения тригонометрических функций
|
|
15
16
|
§ 7. Тригонометрические функции числового аргумента
|
тригонометрической функции числового аргумента, основные формулы тригонометрических функций одного аргумента.
|
упрощать выражения с применением основных формул тригонометрических функций одного аргумента
|
Тригонометрические функции
|
|
17
18
|
§ 8. Тригонометричес кие функции углового аргумента
|
понятие тригонометри ческой функции углового аргумента, понятие радианной меры угла.
|
умение переводить радианную меру угла в градусную и наоборот
|
Тригонометрические функции
|
|
19
20
|
§ 9. Формулы приведения
|
формулы приведения.
|
применение формул
|
Тригонометрические функции
|
|
21
|
Контрольная работа №2
|
проверить теоретические и практические знания по теме: «Тригонометрические функции числового и углового аргумента».
|
|
22
23
|
§10. Функция  , ее свойства и график , ее свойства и график
|
график функции  , свойства функции. , свойства функции.
|
строить графики функций  , , 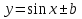 на основе графика на основе графика  . .
|
Свойства числовых функций
|
|
24
25
|
§11. Функция  , ее свойства и график , ее свойства и график
|
график функции  , свойства функции. , свойства функции.
|
строить графики функций  , , 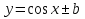 на основе графика на основе графика  . .
|
Свойства числовых функций
|
|
26
27
|
§12. Периодичность функций  , , 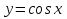
|
понятие основного периода.
|
находить основной период функции.
|
|
|
28
29
30
|
§13. Преобразование графиков тригонометрических функций
|
преобразование функции 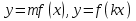 для различных значений коэффициентов для различных значений коэффициентов  . .
|
построения графика функции 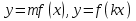 , если известен график функции , если известен график функции  . .
|
Преобразование числовых функций
|
|
31
32
|
§ 14. Функция  , ,  , их свойства и графики , их свойства и графики
|
графики функций 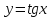 , ,  и их свойства и их свойства
|
|
Свойства числовых функций
|
|
33
|
Контрольная работа №3
|
проверить теоретические и практические знания по теме: «Тригонометрические функции».
|
|
|
|
Глава 3. Тригонометрические уравнения
|
|
34
35
36
|
§ 15. Арккосинус. Решение уравнения 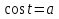
|
понятие  ; формула решения уравнения ; формула решения уравнения 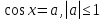
|
Решать уравнения и простейшие тригонометричес кие неравенства на применение этой формулы
|
Понятие косинуса
|
|
37
38
39
|
§ 16. Арксинус и решение уравнения 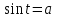
|
понятие  ; формула решения уравнения ; формула решения уравнения 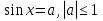
|
Решать уравнения и простейшие тригонометричес кие неравенства на применение этой формулы
|
Понятие синуса
|
|
40
41
|
§ 17. Арктангенс и решение уравнения 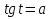 . .
Арккотангенс и решение уравнения 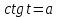 . .
|
понятие  и формулы решения уравнений и формулы решения уравнений  ; рассмотреть уравнения на применение этих формул. ; рассмотреть уравнения на применение этих формул.
|
Решать уравнения  и простейшие тригонометрические неравенства и простейшие тригонометрические неравенства
|
Понятие тангенса, котангенса
|
|
4243
4445
46
47
|
§ 18. Тригонометрические уравнения
|
Два основных метода решения тригонометрических уравнений, алгоритм решения однородных уравнений.
|
решать простейшие тригонометрические уравнения, уравнения со сложным аргументом.
|
|
|
48
|
Контрольная работа №4
|
проверить знания и умение учащихся по теме «Тригонометрические уравнения»
|
|
|
|
Глава 4. Преобразование тригонометрических выражений
|
|
49
50
51
|
§ 19. Синус и косинус суммы и разности аргументов
|
формулы синуса и косинуса суммы и разности аргументов
|
решать задания на применение формул синуса и косинуса суммы и разности аргументов.
|
Синус и косинус
|
|
52
|
§ 20. Тангенс суммы и разности аргументов
|
формулы тангенса суммы и разности аргументов
|
Решать задания на применение формул тангенса суммы и разности аргументов
|
Тангенс
|
|
53
54
55
|
§ 21. Формулы двойного угла
|
формулы двойного угла
|
решать задания на применение формул двойного угла
|
Синус и косинус, тангенс
|
|
56
57
58
59
|
§ 22. Преобразование суммы тригонометрических функций в произведение
|
формулы преобразования сумм тригонометрических функций в произведение
|
решать задания на применение формул преобразования сумм тригонометрических функций в произведение
|
Синус и косинус, тангенс
|
|
60
|
Контрольная работа №5
|
проверить знания и умение учащихся по теме «Преобразование тригонометрических выражений»
|
|
61
|
§ 23.1. Преобразование произведений тригонометрических функций в сумму
|
формулы преобразования произведений тригонометрических функций в сумму
|
Решать задания на применение этих формул.
|
Синус и косинус, тангенс
|
|
62
|
§ 23.2. Преобразование выражения  к виду к виду 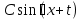
|
формулы преобразования выражения  к виду к виду 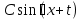
|
решать задания на применение формул преобразование выражения  к виду к виду 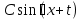 . .
|
Синус и косинус
|
|
|
Глава 5. Производная
|
|
63
|
§ 24. Числовые последовательности и их свойства. Предел последовательности
|
понятие числовой последовательности, способы ее задания, предела последовательности,
свойства сходящихся последовательностей.
|
вычислять пределы последовательностей, решать задания на применение свойств числовых последовательностей.
|
Способы задания функций
|
|
64
|
§ 25. Сумма бесконечной геометрической прогрессии
|
формула суммы бесконечной геометрической прогрессии.
|
|
Геометрическая прогрессия. Сумма 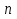
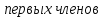
|
|
65
66
67
|
§ 26. Предел функции
|
понятие предела функции на бесконечности, предела функции в точке, понятия приращение аргумента, приращения функции.
|
решать задания на вычисление пределов
|
Функция, область определения
|
|
68
69
70
|
§ 27. Определение производной
|
задачи, приводящие к понятию производной; понятие производной, алгоритм отыскания производной, формулы дифференцирования.
|
Выводить формулы дифференцирования
|
|
|
71
72
73
74
|
§ 28. Вычисление производных
|
правила дифференцирования
|
решать задачи на применение формул и правил дифференцирования и вычисления производной сложного аргумента.
|
|
|
75
|
Контрольная работа №6
|
проверить знания и умение учащихся по теме «Определение производной»
|
|
76
77
|
§ 29. Уравнение касательной к графику функции
|
алгоритм составления уравнения касательной к графику функции 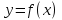 . .
|
решать задания на составление уравнения касательной к графику функции 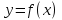 . .
|
|
|
78
79
80
81
|
§ 30. Применение производной для исследования функций на монотонность и экстремумы
|
исследование функции на монотонность и отыскание точек экстремума.
|
|
|
82
83
84
|
§ 31. Построение графиков функций
|
алгоритм исследования непрерывной функции 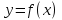 на монотонность и экстремумы. на монотонность и экстремумы.
|
построение графиков функции
|
|
|
85
|
Контрольная работа №7
|
проверить знания и умения учащихся по теме «Производная»
|
|
86
87
88
89
|
§ 32.1. Применение производной для отыскания наибольшего и наименьшего значений непрерывной функции на промежутке
|
отыскания наибольших и наименьших значений непрерывной функции на промежутке, алгоритм отыскания наименьшего и наибольшего значений.
|
решать задачи на отыскание наибольших и наименьших значений непрерывной функции на промежутке.
|
|
|
90
91
92
93
|
§ 32.2. Задачи на отыскание наибольшего и наименьшего значений величин
|
алгоритм отыскания наименьшего и наибольшего значений.
|
решать задачи на отыскание наибольших и наименьших значений величин.
|
|
|
94
95
|
Контрольная работа №8
|
проверить знания и умения учащихся по теме «Производная»
|
|
96
97
98
99
100
101
|
Итоговое повторение
|
|
|
|
|
102
|
Итоговая контрольная работа
|
проверить знания и умения, учащихся по курсу 10-го класса
|
Контрольно – измерительные материалы:
Л.А. Александрова Алгебра и начала анализа. Самостоятельные работы 10 класс. – М.: Мнемозина, 2006;
А.Г. Мордкович, Е.Е. Тульчинская. Алгебра и начала анализа, 10 – 11 класс. Контрольные работы. – М.: Мнемозина, 2005;
Л.О. Денищева, Т.А. Корешкова. Алгебра и начала анализа, 10 – 11 класс. Тематические тесты и зачеты. – М.: Мнемозина, 2006;
Ф. Ф. Лысенко Математика ЕГЭ – 2007, 2008 . Вступительные экзамены. – Ростов-на-Дону: Легион;
С. М. Саакян, А.М. Гольдман, Д.В. Денисов Задачи по алгебре и началам анализа 10-11 класс. – М.: Просвещение, 1990.
Литература:
А.Г. Мордкович Алгебра и начала анализа.10-11 класс. Учебник. – М.: Мнемозина, 2005;
А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская Алгебра и начала анализа.10-11 класс. Задачник. – М.: Мнемозина, 2005;
А.Г. Мордкович Алгебра и начала анализа.10-11.Методическое пособие для учителя. – М.: Мнемозина, 2005;
Башмаков М.И. Математика. Практикум по решению задач. Учебное пособие для 10 – 11 классов гуманитарного профиля. М., Просвещение, 2005;
Ивлев Б.И., Саакян С.И., Шварцбург С.И., Дидактические материалы по алгебре и началам анализа для 11 класса, М., 2000;
Лукин Р.Д., Лукина Т.К., Якунина И.С., Устные упражнения по алгебре и началам анализа, М.1989;
Шамшин В.М. Тематические тесты для подготовки к ЕГЭ по математике, Феникс, Ростов-на-Дону,2004;
Ковалёва Г.И. Учебно-тренировочные тематические тестовые задания с ответами по математике для подготовки к ЕГЭ, ч. I,II,III, Волгоград,2004;
Студенецкая В.Н. Математика: система подготовки учащихся к ЕГЭ, Волгоград,2004;
Математика. Еженедельное приложение к газете «Первое сентября»;
Математика в школе. Ежемесячный научно-методический журнал.
|
|
|
 Скачать 135.53 Kb.
Скачать 135.53 Kb.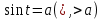 и
и 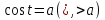 , формулы
, формулы  и
и 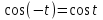
 , ее свойства и график
, ее свойства и график ,
, 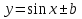 на основе графика
на основе графика  , ее свойства и график
, ее свойства и график ,
, 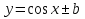 на основе графика
на основе графика 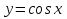
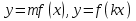 для различных значений коэффициентов
для различных значений коэффициентов  .
.  .
. ,
,  , их свойства и графики
, их свойства и графики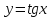 ,
,  и их свойства
и их свойства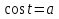
 ; формула решения уравнения
; формула решения уравнения 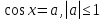
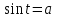
 ; формула решения уравнения
; формула решения уравнения 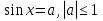
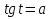 .
.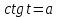 .
. и формулы решения уравнений
и формулы решения уравнений  ; рассмотреть уравнения на применение этих формул.
; рассмотреть уравнения на применение этих формул. и простейшие тригонометрические неравенства
и простейшие тригонометрические неравенства  к виду
к виду 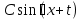
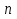
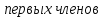
 .
.