Конспект урока алгебры и начал анализа в 10 классе по теме «Производные тригонометрических функций»

Скачать 85.16 Kb. Название Конспект урока алгебры и начал анализа в 10 классе по теме «Производные тригонометрических функций» Дата 05.03.2016 Размер 85.16 Kb. Тип Конспект

Конспект урока алгебры и начал анализа в 10 классе по теме «Производные тригонометрических функций» Цель и задачи урока: Создание на уроке условий для совершенствования знаний учащихся по нахождению производной тригонометрических функций. Дальнейшее развитие умений работать самостоятельно, анализировать, сравнивать, ориентироваться в выборе рациональных приемов и способов решения заданий. Продолжить работу по формированию приемов самоанализа и самооценки. Оборудование: тест, презентация, мультимедиапроектор, компьютер Ход урока 1 этап. Мотивационно-целевой Воспроизведение вместе с учащимися темы предыдущего урока, узловых моментов изучаемого материала. СЛАЙД 2 Эпиграфом к нашему уроку будут слова Конфуция: Скажи мне, и я забуду. Покажи мне, и я запомню. Дай мне действовать самому, И я научусь! На прошлых уроках мы познакомились с правилами вычисления производных, выучили формулы дифференцирования, научились находить производные сложных функций. 2 этап. Актуализация знаний Блиц-опрос (СЛАЙД 3) Тренажер (СЛАЙД 4) 3 этап. Организация деятельности по реализации поставленных задач - Производные каких функций мы уже умеем находить? ОТВЕТ: линейной, степенной, обратной пропорциональности. - Какие функции вы изучили в 10 классе? ОТВЕТ: тригонометрические. - Умеем ли мы находить их производные? ОТВЕТ: нет. - Значит, с чем мы должны сегодня познакомиться? ОТВЕТ: с производными тригонометрических функций. Задание (таблица) Продифференцировать: а) f (x) = sin2 x + cos2 x б) f (x) = tg 0 + x3 в) f (x) = sin 2x СЛАЙД 5 этап. Формирование новых знаний 1. Докажем, что функция sin x имеет производную в любой точке и (sin x)´= cos x Доказательство ведет ученик, пользуясь схемой вычисления производной функции f в точке хо. 2. Формулы дифференцирования косинуса, тангенса и котангенса: функции у= cos x, у= tg х, у= сtg х имеют производные в каждой точке области определения и справедливы формулы: 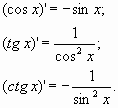а) Работа по учебнику с формулой (cos x)´= sin x б) Самостоятельный вывод формул производной тангенса и котангенса по вариантам СЛАЙД 6 5 этап. Применение новых знаний Выполнение №231 (а), 232 (а), 233(а) СЛАЙД 7 Самостоятельная работа: №231 (б), 232 (б), 233 (б) Проверка через слайд СЛАЙД 8 Проверь себя СЛАЙД 9 СЛАЙД 10 Готовимся к ЕГЭ СЛАЙД 11 Контроль усвоения: Вариант 1 Вариант 2 Y= sin2x 1. sin 2x 2. 2sin x 3. –sin 2x Y= cos2x 1.- sin 2x 2. sin 2x 3. 2sin x Y = 3cos 2 x 1. 6sin 4x 2.-3sin 2x 3. -6sin 2x Y= 3sin 2x 1.3cos 2x 2. 6cos 2x 3. -6cos 4x Y= 4tg 3x 1.4/cos2 3x 2. 4/cos2х 3. 12/cos2 3x Y= 3ctg2x 1. -3/sin2 2x 2. 6/sin2 2x 3.- 6/sin2 2x КОД: 1 вариант -133 2 вариант -123 6 этап. Домашнее задание - дифференцированное: СЛАЙД 12 П.17, №236(в,г), 237 (а,б), повторить формулы Найти производные данных в таблице функций. Ответы записать в таблицу. Проверка – через высказывание Паскаля y y' Буква № окошка cos²π– 4x2 + 7 – 8x А 15 1/tgπ/4  + 3x2 6x Б 25 1/x + 5 - В 1,12,16 x6 – 4sinx 6x5 – 4cosx Г 18 20x4  - cosx 80x3 + sinx Е 2,7,9,13,17 2sin4x+16 8cos4x И 4,6,30,35 sin²x + 13 sin2x К 14 cos² 2x sin4x Л 3,10,34 2x6 + (sinx)/2 12x5 + ½(cosx) М 31 - 5х 7x5 – 20x3 Н 26 x²sin2x 2xsin2x + 2x²cos2x О 11,19,12,24,27 - ctg3x + 3/(sin²3x) П 21 sinx+ tg6x 5xcosx+  Т 29,36 x+ 3sinx/3 1 + cosx С 20,23,28,33 2x3 – x2 + x 6x2 – 2x + 1 Ч 5,8 x/cosx Ы 32 sin6xcos3x+cos6xsin3x 9cos9x Ь 37 1 2 3 4 5 6 7   8 9 10 11 12 13 14 15   16   17 18 19                                             20 21 22 23 24 25 26 27 28 29 30   31 32 33 34 35 36 37                                                   Величие человека - в его способности мыслить. Блез Паскаль (1623-1662) 7 этап. Подведение итогов Продолжите фразу: - Сегодня на уроке я узнал … - Сегодня на уроке я научился … - Сегодня на уроке я познакомился … - Сегодня на уроке я повторил … - Сегодня на уроке я закрепил … № п/п Этап урока Деятельность учителя Деятельность ученика Время (мин.) Д.Гильберта: «Математическую теорию можно считать совершенной только тогда, когда ты сделал ее настолько ясной, что берешься изложить ее содержание первому встречному». Деятельность учителя Деятельность учащихся отвечает на вопросы учащихся; объясняет решение заданий, вызвавших затруднения;