Подготовка к егэ

Скачать 65.82 Kb. Название Подготовка к егэ Дата 10.02.2016 Размер 65.82 Kb. Тип Изложение

Разработка урока По математике в 11 классе Тема: Подготовка к ЕГЭ Задачи С6 на тему «Целочисленное решение» Учитель Москвина Л.Ю. МОБУ СОШ с.Амзя г.Нефтекамск 2011 год Разработка урока по математике в 11 классе Задачи С6 по теме «Целочисленное решение» Цели: Дидактическая: Научить способам и приемам решений целочисленных преобразований. Техническая: Формировать общие способы и приемы решения задач С6 на целочисленное преобразование. Воспитательная : воспитание интереса к решению и овладению приемам решений нестандартных заданий части С6 по ЕГЭ. a=5 b=3 a=-5 b=-3 Выравнивание знаний a2-b2=? 5*3  a*b=15 -5*(-3) n!=1*2*…*n произведение всех натуральных чисел от 1 до n например 5!= 1*2*3*4*5 если а-2b=1 2b –четное число, т.к. кратно 2, то a – нечетное  а=2n+1 (m+3)2=? m2+6m=y Искусственно получить или выделить квадрат Изложение нового материала Решить в натуральных числах уравнение n!+5n+13= k2 Решение Предположим, что n>=5, то n! делиться на 2 и на 5 (n!=1*2*3*4*5*…n), значит запись числа в левой части равенства оканчивается на 3 или 8 ,но правая часть квадратного числа не может оканчиваться на 3 и 8 если n€[1;4], то единственное решение n=2; k=5 (2!+5*2+13=52 1*2+10+13=25 – верно) Ответ : n=2; k=5. Решить в целых числах уравнение: m4-2n2=1 (*) Решение: т.к. 2n2 четно, а разность - нечетное число, то m4 – нечетное число; пусть m= 2t+1, т.к. квадрат числа число не отрицательное, то если (m;n) – решение уравнения, то (-m;n); (m;-n); (-m;-n) – тоже решения уравнения. Из (*) следует m4-1=2n2 m4-1=(m-1)(m+1)(m2=1)=(2t+1-1)(2t+1+1)(4t2+4t+2)= =2t(2t+2)(4t2+4t+2)=2n2 8t(n+1)(2t2+2t+1)=2n2 /:2 4t(n+1)(2t2+2t+1)=n2 (**) Левая часть четное число, то n – четное. Пусть n=2z 4t(n+1)(2t2+2t+1)=4z2 /:4 t(n+1)(2t2+2t+1)=z2 2t2+2t+1= 2t(t+1)+1 числа t; t+1; 2t(t+1)+1 - попарно взаимно простые, а их произведение – полный квадрат. Это возможно, если t=0, иначе t+1 не будет квадратом. 0*1*1=z2 z2=0 z=0, то n=0, m=±1 ответ: m=±1, n=0 Решить в целых числах – разбираем вместе. n2=9m2+7 n2-9m2=7 используем формулу разности квадратов. (n-3m)(n+3m)=7 7= 7*1=1*7=-1*(-7)= (-7)*(-1) - 4 варианта. n-3m=1 7 -7 -1 n+3m=7 1 -1 7 6m=6 m=1 n=1+3*1 m=1 n=4 аналогично другие варианты. Ответ: (4;1), (4;-1) ;(±3;-+2); (±5;-+2) Найти все пары натуральных чисел, разность квадратов которых равна 33. Решение: 1)Найдем все пары чисел (а,b), a,bЄN, что a2-b2=33 (a-b)(a+b)=33 33=1*33=33*1=11*3=3*11 т.к a+b>a-b, то возьмем 33=1*33 =3*11. a-b=1 a+b=33 a=1+b 2b=32 a=17 b=16 a-b=3 a+b=11 a-3+b 2b=8 a=7 b=4 Ответ: (17;16); (7;4) 5.Найти все целые значения при которых число 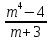является целым. Решение: 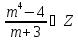То, 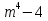должно делиться на m+3 Искусственно получим в числителе квадрат двучлена (m+3) m2-4=(m2+6m+9)-6m-9-4=(m+3)2-6m-13 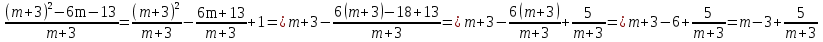Т.к. m-3∊Z, то ищем при каких m 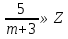Перебираем. Если m=-8, то 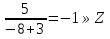Если m=-4, то 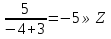Если m=-2, то 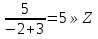Ответ: -8;-4;-2;2. 6.Найти все пары целых чисел х и у, при которых является верным равенство -3ху-10х+13у+35=0 Решение: -3ху-10х+13у+35=0 /*(-3) 9ху+30х-39у-130+130-105=0 3х(3у+10)-13(3у+10)+25=0 3х(3у+10)-13(3у+10)+25=0 (3у+10)*(3х-13)=-25 6 способов разложения: -25=-1*25=1*(-25)=25*(-1)=-25*1=-5*5=5*(-5) 1 3х-13=1 3у+10=-25 х=4/3 у=-35/3 Не удовлетворяет условию 2 3х-13=-1 3у+1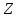0=25 х=4∊ у=5∊ 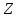3 3х-13=5 3у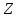+10=-5 х=6∊ у=-5∊ 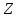4 3х-13=-5 3у+1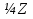0=5 х=8/3 у=-5/3 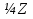Не удовлетворяет условию 5 3х-13=25 3у+10=-1 х=38/3 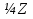у=-11/3 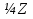Не удовлетворяет условию 6 3х-13=-25 3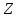у+10=1 х=-4∊ у=-3∊ 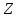Ответ: (4;5);(6;-5);(-4;-3) 6. Решить в натуральных числах уравнение: 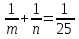Решение: уравнение тождественно 25m+25n=mn, где m>n При n=25 равенство неверно 25*25+25m=25m 625=0 - неверно. Выразим число m m(25-n)=-25n m(n-25)=25n m= 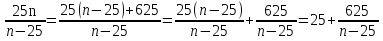выясним, при каких m 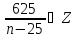натуральные делители 625: 1;5;25;125;625 n-25=1 n=26, то m=650 n-25=5 n=30, то m=150 n-25=125 n=150, то m=30 30>150 -неверно n-25=625 n=650, то m=26 26>650- неверно ответ: m=650; n=26 или m=150; n=30. 7.Решить в целых числах уравнение 4*3х-35=у2 Решение: 1)Если (х;у) – решение уравнения, то (х;-у) – тоже решение. Рассмотрим вначале решение где у≥0 2)Рассмотрим два случая Х- четное, т.е. х=2n, n∊N,то выражение можно разложить как разность квадратов. 4*32n-у2=(2*3n-у)(2*3n+у)=35 35=5*7=1*35 2*3n-у<2*3n+у ± 2*3n-у=5 2*3n+у=7 4*3n=12 2у=2 n=1 у=1 ± 2*3n-у=1 2*3n+у=35 4*3n=36 2у=34 n=2 у=17 2 случай если х – нечетное, х=2n+1, n∊N, 4*3х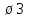, а у2не делится на 3, дает в остатке 1 или 0, а число 35:3 (ост 2) следовательно уравнение не имеет решений. Ответ: (2;1) и (2;-1); (4;17); (4;-17) Итог урока: применение формул ФСУ, искусственное получение выражений, кратных данным знаменателю, учет четности и нечетности слагаемых, способы разложения на числовые множители и др. дают нам способы решения целочисленных выражений. IV Домашнее задание: 1)повторение способов; 2)закрепление их при решении следующих заданий С6. а) Найти все пары натуральных чисел, разность квадратов которых равна 77 Ответ: (9;2); (39;38) б)Найти все натуральные значения n, при которых число 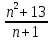является натуральным. Ответ:1;6;13 в) Решить в целых числах 2х-63=у2 Ответ: (6;1); (6;-1); (10;31);(10;-31)