План-конспект урока № Геометрия 11 класс. Система координат в пространстве. Простейшие задачи в координатах Цели урока

Скачать 22.88 Kb. Название План-конспект урока № Геометрия 11 класс. Система координат в пространстве. Простейшие задачи в координатах Цели урока Дата 05.04.2016 Размер 22.88 Kb. Тип План-конспект

План-конспект урока № 5. Геометрия 11 класс. Система координат в пространстве. Простейшие задачи в координатах Цели урока: - Изучить определение и свойства вектора системы координат в пространстве - Научить учащихся пользоваться этим определением на практике - Уметь находить координаты векторов, середина отрезка, сумму и разность векторов - Повторение ранее изученного материала. - Формирование умения решать задачи. - Реализация принципов связи теории и практики. - Развитие памяти, речи, любознательности, познавательного интереса. - Развитие аккуратности при выполнении чертежей. Ход урока. 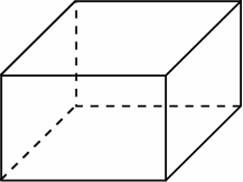Разобрать определение системы координат в пространстве. Дан прямоугольный параллелепипед AD = 4, DC = 3, CC1 = 6, M - середина AA1, Q середина DC, N середина BC. Найти: Середину отрезков AC, DC1, CB1, BC1, AN, NQ Длины векторов AC, A1C, BD1, BD, D1D1, NQ, ND,QB1 Вычислить сумму или разность векторов: B1C1 + DB, AC + BC1, BB1 – CA1, NA + ND1, BD - CN Поверить конспект параграфа «Простейшие задачи в координатах». Домашнее задание: Дан куб с ребром 4. M - середина AA1, K середина BC, N середина DB. Найти: Координаты векторов: KB1, D1K, CM, DN Длины векторов: DC, CN, AK, BM. Координаты середины отрезка: DA, BC1, MN, KA, KN.