«Основное свойство дроби»
 Скачать 59.53 Kb. Скачать 59.53 Kb.
|
| Тема: «Основное свойство дроби». Класс: 5 класс. Тип урока: изучение нового материала. Оборудование и материалы:
Цели:
План урока:
Ход урока: 1.Организационный момент. Здравствуйте, ребята! Садитесь! Сегодня на уроке мы с вами будем работать с обыкновенными дробями. Для этого мы вспомним, что мы знаем об обыкновенных дробях, а потом сами выведем новое свойство дроби. Научимся применять это свойство на практике. Слайд 1. Итак, запишем в тетрадях число и тему урока «Основное свойство дроби». (Дублируется на доске.) 2. Актуализация опорных знаний учащихся. Слайд 2.
Слайд 3.
Слайд 4.
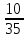 , , 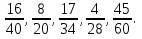 (5, 8, 4, 17, 4, 15). (5, 8, 4, 17, 4, 15).3.Изложение нового материала. Слайд 5. А сейчас используя модели кругов, проиллюстрируем дроби. Разделим круг на 4 части и 3 из них закрасим. Какая дробь получилась? Второй круг разделим на 8 частей и закрасим 6 из них. Какая дробь получилась? Третий круг разделим на 12 частей и закрасим 9? Какая это дробь? 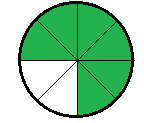 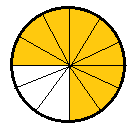 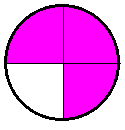 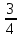 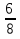 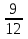 Что вы заметили? Какие дроби получились по величине? (Равные) Можно ли между этими дробями поставить знак равно? (Да) Слайд 6. Как из дроби 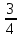 получить дробь получить дробь 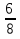 ? (Надо числитель и знаменатель умножить на ? (Надо числитель и знаменатель умножить на 2) Слайд 7. Как из дроби 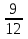 получить дробь получить дробь 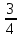 ? (Надо числитель и знаменатель разделить на 3) ? (Надо числитель и знаменатель разделить на 3)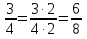 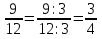 Слайд 8. Какие действия мы выполнили, чтобы получить дроби равные данным? (Для получения дроби равной данной, надо числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число) Слайд 9. Мыс вами сформулировали очень важное свойство дроби. Основное свойство дроби. Запишите в тетрадях. Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь. Слайд 10. Физкультминутка. Руки вверх вы поднимите, И ладошки покажите. И не раз, а раза три, Ну-ка дружно повтори. А теперь пожмём плечами, Покиваем головами. Улыбнёмся. Сядем прямо. Вы прекрасны, без изъяна! 4. Закрепление, отработка нового материала. Слайд 11. №1. (устно) Торт разрезали на 8 равных частей. Одну из них разрезали еще на 2 равные части. Какую часть пирога составляет одна маленькая часть? 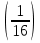 №2. Рисунок на доске. Объясните, почему равны дроби. (Мы круг разделили на 5 равных частей и закрасили 3 таких части. Затем каждую пятую часть круга мы разделили еще на 3 равные части. Тогда весь круг оказался разделенным на 5  3=15 частей, а в трех пятых круга будет 3 3=15 частей, а в трех пятых круга будет 3 3=9 таких частей, поэтому 3=9 таких частей, поэтому 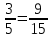 ). ). Слайд 12. Историческая справка. Интересная система дробей была в Древнем Риме. Она основывалась на делении на 12 долей единицы веса, которая называлась асс. Двенадцатую долю асса называли унцией. Например, римлянин мог сказать, что он прошел семь унций пути или прочел пять унций книги. При этом, конечно, речь шла не о взвешивании пути или книги. Имелось в виду, что пройдено 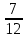 пути или прочтено пути или прочтено 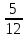 книги. А для дробей, получающихся сокращением дробей со знаменателем 12 или раздроблением двенадцатых долей на более мелкие, были особые названия. Для облегчения работы составлялись специальные таблицы, некоторые из которых дошли до нас. книги. А для дробей, получающихся сокращением дробей со знаменателем 12 или раздроблением двенадцатых долей на более мелкие, были особые названия. Для облегчения работы составлялись специальные таблицы, некоторые из которых дошли до нас.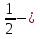 «семис» «семис»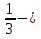 «триенс» «триенс»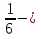 «секстанс» «секстанс»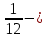 «унция» «унция»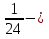 семиунция семиунция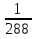 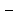 «скрупулус» «скрупулус»Слайд 13. 1. (устно) Выразите в унциях: половину, треть, четверть, пять шестых, три четверти. (Полвина 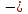 6 унций, треть 6 унций, треть 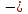 4 унции, четверть 4 унции, четверть 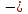 3 унции, пять шестых 3 унции, пять шестых 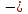 10 унций, три четверти 10 унций, три четверти 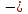 9 унций.) 9 унций.)2. (на доске и в тетрадях) 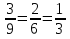 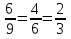 Какой вывод можно сделать? (Равные дроби на координатном луче изображаются одной и той же точкой). 3. Умножить числитель и знаменатель дроби на 5. (на доске и в тетрадях) 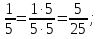 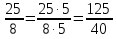 ; ;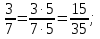 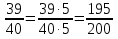 . .Что мы можем сказать о данных дробях? (Они равны) Как из данных дробей мы получили новые дроби? (Мы числитель и знаменатель умножали на одно и то же число) Чем мы пользовались? (Основным свойством дроби) 4. Сократить дроби. (с комментированием на месте) 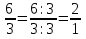 ; ; 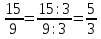 ; ;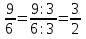 ; ; 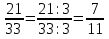 . .Что мы можем сказать о данных дробях? (Они равны) Как из данных дробей мы получили новые дроби? (Мы числитель и знаменатель делили на одно и то же число) Чем мы пользовались? (Основным свойством дроби) Слайд 14. № 3. (письменно в тетрадях). Выберите равные дроби и запишите в тетрадь. 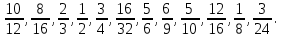 Поменяйтесь тетрадями и выполните проверку. Ответ 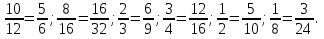 Слайд 15. № 770(после разбора решить самостоятельно) Для числителя и знаменателя каждой дроби найти НОД, разделить числитель и знаменатель дроби на найденное число. Слайд 16. 5. Постановка домашнего задания. Откроем дневники, запишем домашнее задание. Выучить правило п.4.2, стр. 169, решить № 763, 766(б, г), 769(б, в). Оценки за урок. Слайд 16. 6.Подведение итогов урока. Что нового вы узнали сегодня на уроке? Сформулируйте основное свойство дроби. А для тех, кто не точно запомнил это свойство, прочитаем его еще раз. Слайд 17. Спасибо за урок! |
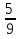 , 3
, 3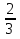 ,
, 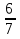 , 10
, 10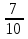 ,
, 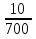 ,
, 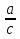 . (Дробь, числитель которой a, а знаменатель с).
. (Дробь, числитель которой a, а знаменатель с).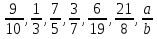 . (Целое разделили на b равных частей и взяли а таких частей).
. (Целое разделили на b равных частей и взяли а таких частей).