«Определение квадратного уравнения. Неполные квадратные уравнения»
 Скачать 75.72 Kb. Скачать 75.72 Kb.
|
| Конспект урока по алгебре. Тема: «Определение квадратного уравнения. Неполные квадратные уравнения». МОУ СОШ № 27 Выполнила: учитель математики и информатики МОУ СОШ №27 Карлышева Е. В. Сухие строки уравнений – В них сила разума влилась. В них объяснение явлений, Вещей разгаданная связь. Л.М.Фридман Тема урока: «Определение квадратного уравнения. Неполные квадратные уравнения». Цели урока:
- познакомиться с понятиями: квадратное уравнение и неполное квадратное уравнение; - научиться решать неполные квадратные уравнения.
- развитие мышления, анализа, синтеза, выделение общего.
- становление трудовых качеств, развитие интереса к предмету. - развитие коллективизма. Тип урока: изучение нового материала. Оборудование: проектор, экран, программное обеспечение, наглядный материал (презентация), раздаточный материал (карточки, таблица с методами решения неполных квадратных уравнений). Ход урока. 1. Организационный момент. Ребята! Квадратное уравнение – это фундамент, на котором построено огромное здание алгебры. Квадратные уравнения применяются начиная с 8-го класса и до окончания вуза. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных уравнений и неравенств. 2. Изучение нового материала. 1. Историческая справка. Простые уравнения люди научились решать более трех тысяч лет назад в Древнем Египте, Вавилоне и только 400 лет назад научились решать квадратные уравнения. Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардом Фибоначчи. Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из этой книги переходили почти во все европейские учебники XIV-XVII вв. Общее правило решения квадратных уравнений было сформулировано в Европе в 1544 г. М.Штифелем. Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид. Именно в XVI – XVII вв. происходит бурное развитие науки, прежде всего в области математики и естествознания, и на этой основе складывается новое представление о Вселенной. 2. Задача, приводящая к квадратному уравнению. Прежде, чем приступить к теме урока, я хочу предложить вам одну задачу. Эта задача пришла к нам из Древней Индии XII века и носит название задача Бхаскары. На две партии разбившись, Забавлялись обезьяны. Часть восьмая их в квадрате В роще весело резвилась. С криком радостным часть восьмая Воздух свежий оглашали. Вместе сколько ты скажи мне, Обезьян там в роще было? Решение задачи: Пусть х – количество обезьян в роще. 1 партия – (1/8х)² 2 партия – 1/8х Составим и решим уравнение: (1/8х)² + 1/8х = х, 1/64х² + 1/8х – х = 0, х² + 8х – 64х = 0, х² - 56х = 0. 3. Определение квадратного уравнения. Получили уравнение, которое нам ещё не знакомо и узнать пока сколько же было обезьян не сможем. Но к концу урока, вы сами мне уже сможете ответить на вопрос задачи. Так что же уравнение мы получили? Такое уравнение называется квадратным. Т. е. уравнение вида: ax² + bx + c = 0, (а ≠ 0), где х – переменная, a – первый коэффициент, b – второй коэффициент, c – свободный член. Как вы думаете, почему уравнение такого вида называются квадратными? Индивидуальная работа по карточкам №1. №1. Определите коэффициенты и свободные члены в уравнениях:
4. Определение неполного квадратного уравнения. Давайте попробуем определить коэффициенты в задаче Бхаскары. х² - 56х = 0, a = 1, b = -56, c = 0. Скажите, пожалуйста, чего не хватает в данном уравнении? Если в квадратном уравнении ax² + bx + c = 0, (а ≠ 0), хотя бы один из коэффициентов равен 0 (кроме а), то такое уравнение называется неполным квадратным уравнением. Неполные квадратные уравнения бывают 3 видов: (в каждом из примеров обсуждать вопрос о количестве корней).
Пример: 5х² - 125 = 0, 4х² + 64 = 0, 5х² = 125, 4х² = - 64, х² = 25, х² = - 64, х = ±5. корней нет. Ответ: ±5. Ответ: корней нет. 2) тип ax² + bx = 0 (b ≠ 0) Пример: 4х² + 9х = 0, х(4х + 9) = 0, Х = 0 или 4х + 9 = 0, 4х = -9, х = -2,5, Ответ: -2,5; 0.
5х² = 0, х = 0. Ответ: 0. А теперь решение неполных квадратных уравнений сведём в таблицу, которую я каждому из вас раздам.
Посмотрите на таблицу и ответьте на вопрос: Какое количество корней может иметь квадратное уравнение? 3. Закрепление. Групповая работа по карточкам №2. Делимся на две команды, каждой команде даётся по карточке с заданиями и координатная полуплоскость. Одна из двух координат дана, необходимо решить квадратное уравнение и записать второй координатой корень уравнения. №2. Отметить в координатных полуплоскостях точки, которые являются решениями неполных квадратных уравнений.
В результате у вас должна получиться звезда. 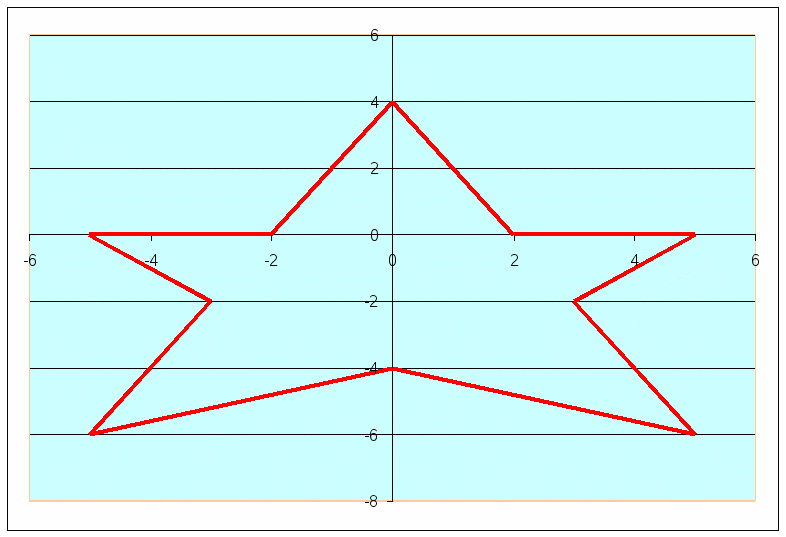 Парная работа по карточкам № 3. Ребята, предлагаю вам следующую игру. Каждому ряду я раздам задания. Первая парта в паре решает первое задание, передаёт карточку второй парте, вторая парта 2 – ое задание решает и передаёт 3 - ей и т. д. Какой ряд быстрее и правильнее решит, тот выиграл. №3. «Цепочка». Решите уравнения. 1 ряд. 2 ряд. 3 ряд.
Сверяют свои ответы с ответами, которые выданы на экране. Вернёмся к задаче, рассмотренной в начале урока, и попробуем ответить на поставленный вопрос. х² - 56х = 0, х(х – 56) = 0, х = 0 или х – 56 = 0, х = 56. Ответ 56 обезьян. 4. Итог урока. 1. С какими новыми уравнениями мы познакомились? 2. Какой вид имеют квадратные уравнения? 3. Какое уравнение называется неполным квадратным уравнением? Домашнее задание: придумать к каждому виду неполного квадратного уравнения примеры, а на следующем уроке мы их с вами будем решать. |