Опыт работы учителя математики Денисоваой Т. В. в реализации технологии укрупнения дидактических единиц на уроках математики на основе деятельностного подхода
 Скачать 235.19 Kb. Скачать 235.19 Kb. |
| Опыт работы учителя математики Денисоваой Т.В. в реализации технологии укрупнения дидактических единиц на уроках математики на основе деятельностного подхода. Преобразования, происходящие в системе образования России в целом, не могли не сказаться на математическом образовании. Каждый неравнодушный учитель задумывается над тем, как сделать процесс обучения эффективным, доступным, направленным на развитие индивидуальности ребенка наряду с воспитание нравственных и других качеств. Перед учителем встает проблема: как уменьшить время обучения, не уменьшая количества информации? Одним из таких эффективных подходов является построение обучения математике на основе уплотнения его содержания. Традиционно педагогический процесс структурировался таким образом, чтобы обеспечить, прежде всего, усвоение знаний, умений и сформировать навыки. Подобная направленность обучения не развивает личность, ориентированную на творчество, приводит к утрате первоначальной любознательности школьников, порождает равнодушие к учению, не обеспечивает формирование способности мыслить самостоятельно, а в некоторых случаях и разрушает способность к мыслительной деятельности, что особенно остро ощущается в среднем звене школы. Все согласны с тем, что нет «царского пути в математику». Много труда и терпения, настойчивости и внимания требуется от учителя и школьника, чтобы последний смог освоить программный минимум знаний по этому предмету. (Эрдниев) Сущность технологии УДЕ сводится к объединению знаний во времени или в пространстве. Элементы знания, разведены по традиции по разным разделам и годам обучения, объединяются и образуют целостный сплав структурно новых знаний. Технология УДЕ реализует системный подход в обучении. Многократный возврат к изучаемому материалу в связи с новыми знаниями, «движение по спирали» к более глубокому их усвоению может быть осуществлено лишь при системном подходе к обучению, когда вопрос о целесообразности и времени возврата к ранее изученному решается на основе анализа всей совокупности подлежащих усвоению единиц информации и взаимосвязей между ними. Переработка информации мозгом человека осуществляется на подсознательном и сознательном уровнях одновременно. Укрупнению единиц усвоения так же благоприятствует расположение записей структурно связанных упражнений в двух параллельных столбцах, друг против друга. То, что зрительно воспринимается рядом, легче противопоставить и связать логически, словесно. Ключевым упражнением по УДЕ является составление и решение обратных задач. В методике составления и решения взаимообратных задач наиболее цены не, сколько сами процессы решения задач как таковых, а переосмысление их содержания с возвратом к первоначальным рассуждениям, то есть составление новых фраз на базе известных слов и чисел. Обратная задача для школьника – это своего рода исследовательская задача. В математике слишком многие элементы изучаются порознь, вместо того чтобы в соответствии с логикой их связей изучать совместно, чтобы образовать систему знаний, которая, подобно живому кристаллу, была бы устойчива по отношению к разрушающему воздействию времени. Понятие укрупнения дидактических единиц достаточно обширно, оно вбирает следующие взаимосвязанные подходы к обучению:
Главнейшей особенностью укрупненной единицы усвоения является то, что она создаёт условия для постижения богатства связей и переходов между компонентами единого знания. При таком подходе учащиеся на уроках больше рассуждают, больше производят самостоятельно мыслительных операций. Это объяснимо дидактически: укрупнение единиц усвоения обязательно приводит к возрастанию информационного потока, проходящего в единицу времени через органы восприятия школьниками. Урок математики, построенный сознательно на необходимости укрупнения знаний, заботится об окружении основного понятия, о наращивании знаний вокруг логического ядра урока, о повторении материала через его развитие, преобразование. Обратные задачи уместно вводить, начиная с элементарных заданий, используемых для проверки сообразительности. Например, работая в 5-х классах, использую задания:
1, 2, 4, 8, 10, 20, 22, 44, 46 ….
Дописать ещё несколько членов ряда.
В ходе изучения геометрии я пришла к выводу, что некоторые темы усваиваются лучше, если их изучать с помощью технологии укрупнения дидактических единиц. Прямую и обратную теорему рассматриваю одновременно. Делим лист на две половины – слева записываем прямую теорему, доказывая вместе, а справа ученики формулируют, записывают обратную теорему и самостоятельно доказывают её. Так, изучение темы, в 7 классе, «Параллельные прямые» строю следующем образом:
При заполнении таблицы, учащиеся впервые встречаются с понятием прямая и обратная теорема, и они наглядно, с помощью таблицы видят, как составить обратную теорему.
На признаки параллельности прямых отводится 3 урока и на свойства параллельности прямых 4 урока. При таком подходе на рассмотрение теоретического материала уходит один урок, остальные уроки идут на решение задач. При изучении темы «Прямоугольные треугольники», свойства 20 и 30 доказываем с ребятами вместе, и записываем в виде таблицы:
При изучении темы «Параллелограмм, его свойства и признаки» в 8 классе, на первом уроке ввожу определение параллелограмма, и совместно изучаем свойства и признаки, оформляя в тетради и на доске таблицу свойства и признаки параллелограмма, а на последующих двух уроках идет отработка и контроль знаний, умений и навыков.
Точно так же поступаю при изучении темы «Прямоугольник. Ромб. Квадрат». На первом уроке вводится определение прямоугольника, рассматриваются его свойства и признаки (в таблице), вводится определение ромба и квадрата, рассматриваются их свойства.
Эффект укрупнения основан на том, что одни и те еж слова, входящие в состав как прямой, так и обратной теорем, фиксируются в памяти как бы однократно; преобразование же теоремы в обратную сводится к перестановке уже воспринятых слов. Поэтому формулирование и доказательство обратной теоремы осуществляется в несколько раз быстрее, чем прямой теоремы. Это дает возможность больше времени отводить решению задач. В программе обучения содержатся и другие группы взаимосвязанных вопросов, которые изучаются раздельно. По характеру мыслительных процессов они совершенно сходны, поэтому целесообразно изучать одновременно взаимно обратные действия и операции. Так при изучении распределительного закона умножения в пятом классе, рассматриваем две операции, которые выполняются с помощь этого метода: РАСКРЫТИЕ СКОБОК  С (А + В) = СА + СВ  ВЫНЕСЕНИЕ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ Раскрыть скобки Вынести общий множитель за скобки  4(х + 3) = 4х + 12 4х + 12 = 4(х + 3) 4(х + 3) = 4х + 12 4х + 12 = 4(х + 3)3(с + 5) = 3с + 15 3с + 15 = 3(с + 5) 2(у – 7) = …….. 2у – 14 = …….. При совместном изучении тем «Нахождение дроби от числа» и «Числа по его дроби» решение задач записываем в таблицу.
При изучении темы «Прямо пропорциональная зависимость» и «Обратно пропорциональная зависимость» рассматриваем сначала таблицу зависимости между тройками некоторых величин, с которыми неоднократно встречаемся при решении задач, а затем решение задач записываем в таблицу.
После отработки этой темы, переходим к рассмотрению задач с помощью пропорций. Сначала составляем алгоритм решения задач с помощью пропорций:
Затем записываем примеры в виде таблицы:
Так понятие пропорция и проценты лучше изучать вместе в 5 классе, причем решение любого вида задач на проценты сводится к единообразному алгоритму составления пропорции. Этот метод совместного изучения всех видов задач на проценты хорошо отражен в следующей таблице:
Важно подчеркнуть, что все три вида задач на проценты решаются единым алгоритмом, основанном на выполнении следующих последовательности шагов:
При такой методике укрупнённой подачи знаний исчезает необходимость изучения темы «Проценты» в трёх отдельных подтемах, т.е. становится ненужным ни запоминание названия вида задачи, ни запоминания словесных правил решения каждого вида задач в отдельности. Этот пример способствует существенному улучшению качества знаний при объединении в одном разделе логически родственных вопросов. В 9 классе изучаю совместно арифметическую и геометрическую прогрессии. На изучение арифметической прогрессии отводится 4 часа, а геометрической – 5 часов по плану, причем по одному часу от каждой темы берётся на изучение новой темы, а на отработку умений отводится 3 и 4 часа соответственно. Применяя технологию укрупнения дидактических единиц, мы на первом уроке знакомимся с основными понятиями и формулами, записывая их в таблицу, а на последующих 8 уроках идет отработка применения формул к решению задач, контроль знаний, умений и навыков. Приведу фрагмент первого урока изучения арифметической и геометрической прогрессий. Тема: Арифметическая и геометрическая прогрессии. Цели и задачи урока:
В ходе изучение темы «Степень и её свойства», заполняем следующую схему: Умножать Делить   Степень  а0 = 1 а1 = а  нулевая степень первая степень нулевая степень первая степень    Дробь Произведения (ab)n = an * an Степень (am)n = amn После заполнения схемы переходим к выполнению заданий:
23 22; b4 : b0; x10 : x; 5 25; (2ab)5. 23 : 22; c5 c0; 310 : 39; (xy)3; (23)2; x10 x; 25 25; (a2)7;
58 + 52 = 510; (32)3 = 36; 0,87 : 0,84 = 0,83; (у7)2 = у14; (2 5)2 = 4 25 = 100; х2 у2 = (ху)2; а6 : а4 = а2.
53 54 = 53 4 = 512; 71 = 7; 710 : 72 = 75 ; (- 0,5)14 : (- 0,5)7 = - 0,52 = -0,25; (-2)3 2 = 16; - 32 3 = 27; - 52 + 4 = 29; 5 5 5 5 = 45; 23 + 27 = 210.
(∆)5 = а25; (∆)2 = а10; (а3)2 ∆ = - а24; а6 (а а2)2 = ( а4) ∆; (∆)3 = а3n; (∆)n = a2n; ∆ a3 = a10; (a a4)2 : ∆ = a2; (a3)2 ∆ = a24; ∆ a = a2; a12 : ∆ = a6; ∆ : a5 = a6. При раздельном изучении таких понятий ученики длительное время решают однородные задачи на основе одного правила, и зачастую создается обманчивая видимость успешного усвоения материала. Но после того как «пройдены» порознь обе операции, ученик при решении любой задачи принуждён выбрать один из двух возможных вариантов рассуждения. Вот тут-то и обнаруживается неожиданно дефект обучения. Пока каждая тема изучалась в отдельности, дети не встречались с необходимостью выбора операции, и соответствующее умение у них не вырабатывалось. Отсюда возникают массовые ошибки. Каким оптимальным набором упражнений, возможно, достичь целостного и прочного усвоения знаний? Структура одних упражнений такова, что при их выполнении развиваются навыки лишь в прямолинейном применении правил; выполнение других неизбежно связано с осуществлением постоянного контроля, проверки ответа, причём последнее нередко ставится навыком и осуществляется неосознанно. Учащимся на уроке приходится решать один за другим множества примеров вида (3а – 2в) (3а + 2в) с постепенным усложнением многочленов левой части – это классическая форма упражнений. А если вместо данного примера предложить пример деформированного вида: ( то характер мыслительных процессов резко изменится. Решение таких примеров основывается на поисках недостающих звеньев замкнутого круга умозаключений путем анализа всей записи, что превращает мыслительный процесс в более сложный, более содержательный и поэтому лучше развивающий способности ученика. Такие задания естественным образом развивают навыки самоконтроля, совершающегося непроизвольно и даже подсознательно. У учащихся появляется активность при выполнении таких заданий. Знания учащихся будут прочными, если они приобретены не одной памятью, не заучены механически, а являются, продуктом собственных размышлений и проб, и закреплялись в результате его собственной творческой деятельности над учебным материалом. Обучение в школе нужно строить так, чтобы оно представлялось для учащегося серией маленьких открытий, по ступенькам которых ум ученика может подняться к высшим обобщениям. Обычное дело, когда ученик, выучил признаки деления и решает типичную задачу на прямолинейное применение правила: делится ли число 207 на 9? Но совсем другое дело, если предложено деформированное число 53*8, требуется добавить цифры, чтобы число делилось без остатка на 9. (Приложение 1). Идея и метод укрупнения дидактических единиц могут получить и получают развитие в преподавании математики в старших классах. При этом укрупнение дидактических единиц идет, как и в основной школе по принципу решения взаимообратных задач, совместному изучению логически связанных понятий и суждений, при этом широко используется прием обобщения по размерности; основным инструментом приёма служат аналогия сходства и аналогия свойств. Наиболее удобен этот прием при изучении стереометрии, позволяющий органически связать стереометрию (геометрию пространства R3) с планиметрией (геометрию пространства R2). В качестве примера рассмотрим изучение темы «Плоскость, касательная к сфере». Укрупнение дидактических единиц при этом выглядит так:
В старших классах естественно оформлять укрупненную дидактическую единицу знаковой моделью, используя в качестве модели блок-схему, граф-схему или, наконец, компакт-схему. Приведем пример оформления с помощью компакт-схемы. Понятие логарифма. Основное логарифмическое тождество. Свойства логарифма. 1.   ap = N ap = N aloqaN = N 2.
В этом примере работает аналогия свойств, которая избавляет от необходимости рассматривать три теоремы о свойствах. Материал становиться не большим по размеру, информационно ёмким и удобным для запоминания. Существует афоризм: «Образование есть то, что остается после того, как будет забыто всё, что было выучено». | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 . Если при пересечении двух
. Если при пересечении двух  в
в . Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны. с
с  . Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. с
. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. с . Если две параллельные прямые пересечены секущей, то соответствующие углы равны.
. Если две параллельные прямые пересечены секущей, то соответствующие углы равны. . Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны.
. Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны.
 В
В ВСД – равносторонний
ВСД – равносторонний 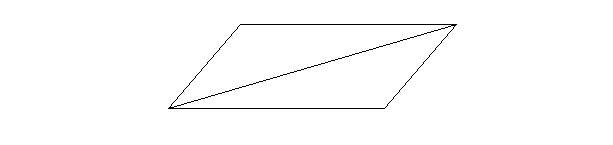 В С
В С

 АВ // СД АД // ВС
АВ // СД АД // ВС

 В
В 
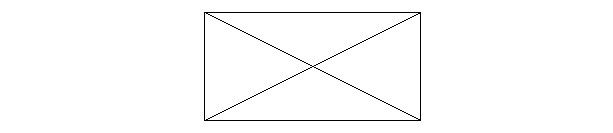
 . ∆ АВД = ∆ ДСА ( по трем сторонам)
. ∆ АВД = ∆ ДСА ( по трем сторонам) 
 Если время уменьшается, то и расстояние тоже уменьшается).
Если время уменьшается, то и расстояние тоже уменьшается). ешение: S = v
ешение: S = v 
 S = 24 км
S = 24 км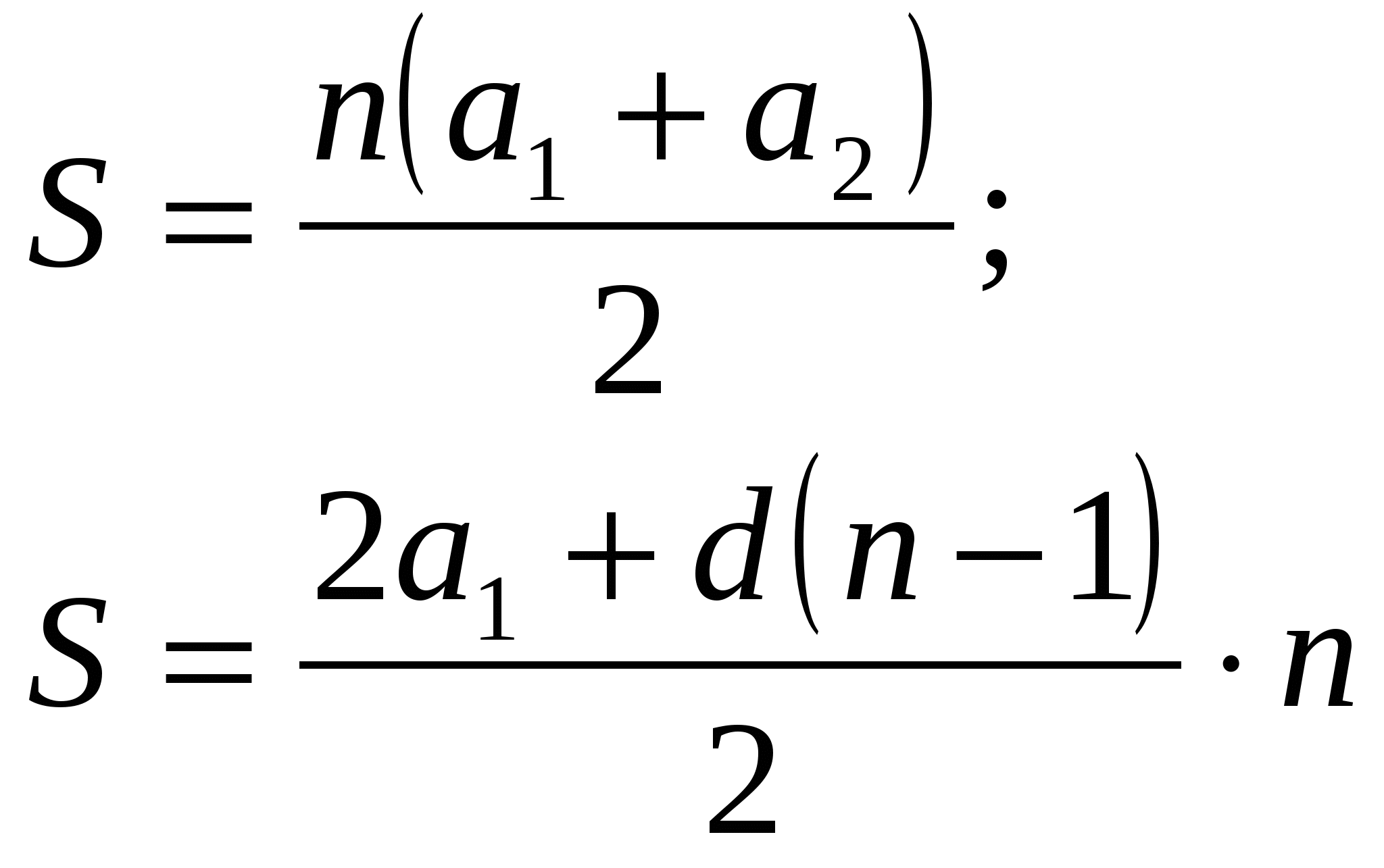
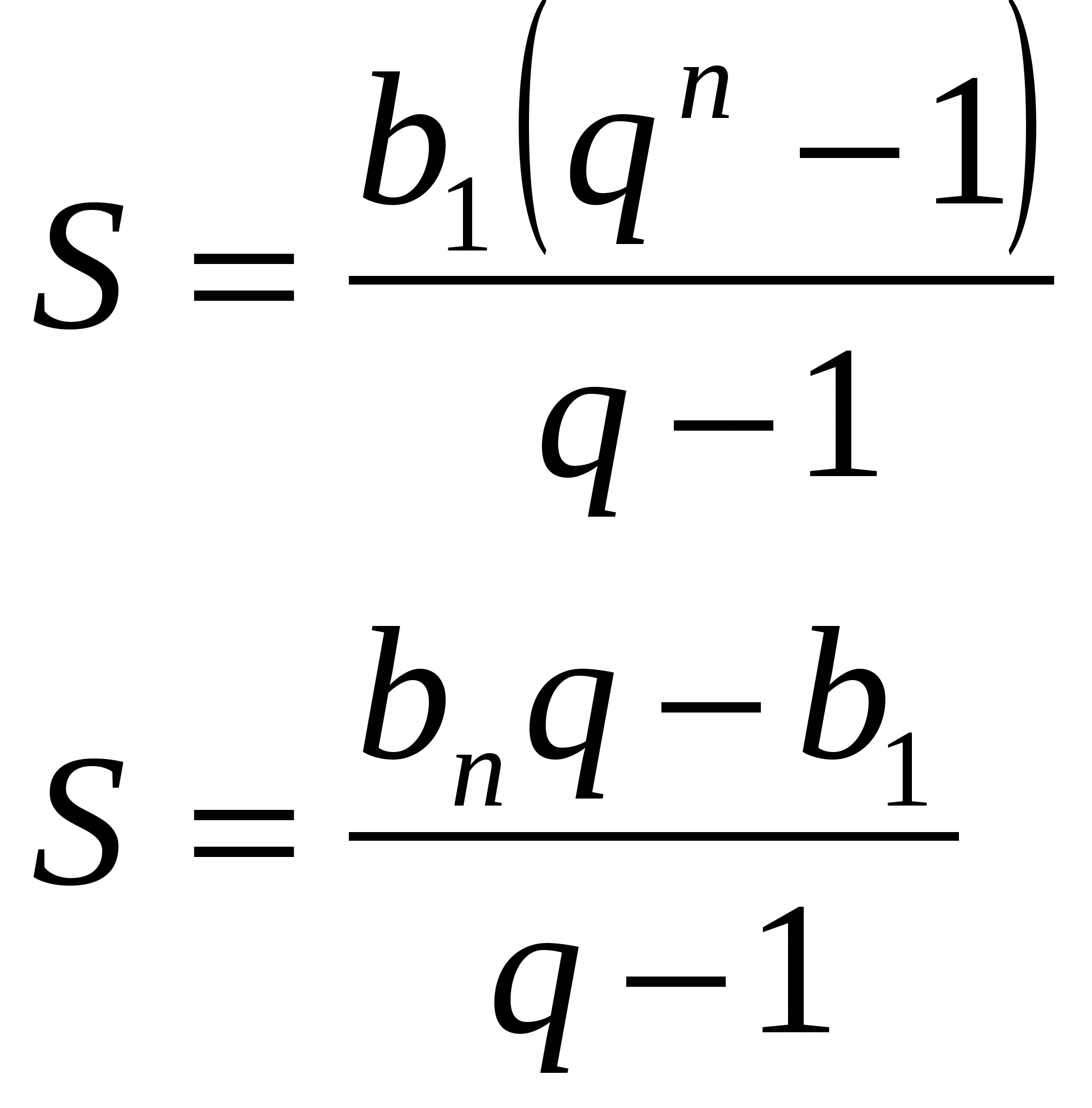 при q
при q