Конспект урока по геометрии в 9 классе по теме «Площадь трапеции» Учителя математики моу «сош c. Большая Осиновка»

Скачать 80.3 Kb. Название Конспект урока по геометрии в 9 классе по теме «Площадь трапеции» Учителя математики моу «сош c. Большая Осиновка» Дата 12.02.2016 Размер 80.3 Kb. Тип Конспект

Конспект урока по геометрии в 9 классе по теме «Площадь трапеции» Учителя математики МОУ «СОШ c. Большая Осиновка» Фоминой Екатерины Александровны I.Образовательные цели урока: 1.Ввести формулу площади трапеции; 2.Закрепить навыки её использования с помощью задач; II .Развивающие цели урока : 3.Развитие у детей умения обобщать, логически мыслить, применять в своих рассуждениях аналогию, наблюдение ,рационально применять свои знания; III.Воспитательные цели урока: 4.Воспитание интереса к математике с помощью элементов занимательности , знакомства с историей возникновения понятия «площадь» Наглядные пособия к уроку: демонстрационная таблица «Площадь трапеции», мел, циркуль , линейка, раздаточные карточки, слайды из презентации к уроку. Содержание урока: ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ Проверка домашнего задания проводится с помощью самостоятельной работы, содержащей задачи , подобные заданным на дом. Взаимопроверка по «ключу». 1 вариант 1.В треугольнике АВС АВ=5см; АС=10см;<А=45°Найдите площадь треугольника АВС. А)50см2 ; б) 25см2 ; в)2 2.В треугольнике АВС а=13см; в=14см ;с=15см. Найдите площадь треугольника АВС. А)42см2 ; б)162 см2 ; в)84см2 . 3.Найдите в прямоугольном треугольнике ( А)4,2см ; б)2,4 см ; в)1,2см 2 вариант 1.В треугольнике АВС АВ=10см; АС=12см;<А=60°Найдите площадь треугольника АВС. А)120см2 ; б) 30см2 ; в) 30см 2 2.В треугольнике АВС а=51см; в=52см ;с=53см. Найдите площадь треугольника АВС. А)234 см2 ; б)1170 см2 ; в)90см2 . 3.Найдите в прямоугольном треугольнике ( А)9,6см ; б)4,8 см ; в)2,4см Ответы : 1 вариант 2 вариант 1 2 3 1 2 3 в в б в б б II .ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА. Актуализация опорных знаний. Вопросы классу:1. Дайте определение трапеции; 2.В чём заключается свойство средней линии трапеции ?; 3.Что называют высотой трапеции? Проблемная ситуация: Найдите площадь трапеции ,представленной на рисунке: 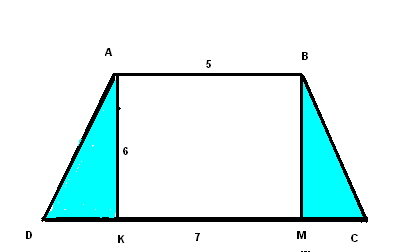Возможное предложение решения №1: №2: 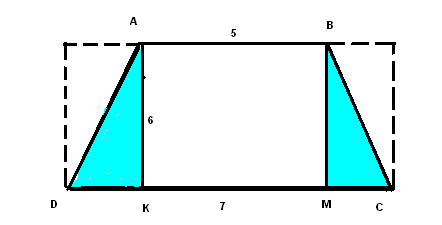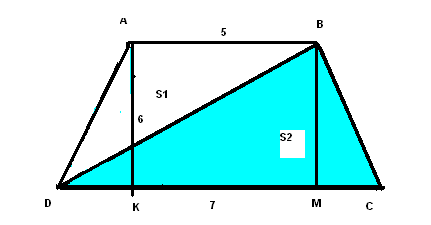Возможные предложения детей:1.S =S+SАКМВ+SВМД (найти не представляется возможным) 2.SАВДС =SАВС +SСВД= 6•7• +6•5• = •6. Затем появляется у учащихся в тетрадях запись темы урока: « Площадь трапеции» Теорема доказывается в соответствии с материалом учебника (площадь трапеции выражается через сумму площадей треугольников, аналогично способу, предложенному в задаче) М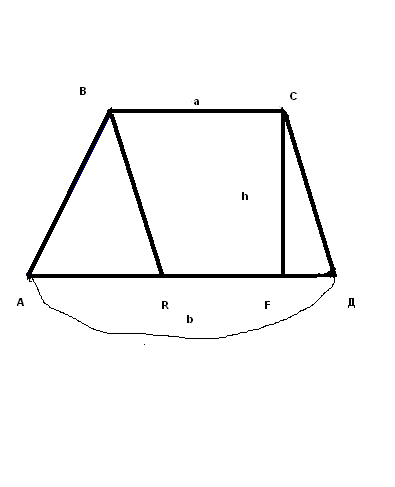ожно показать ещё один способ: В данном случае площадь трапеции разбивается на сумму площадей параллелограмма и треугольника с общей высотой SАВСД = SАВR+SDRВС = =(b-a)∙h +a·h =( bh-ah ) + a h = =· h Ш.ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО: 1.В трапеции АВСД (ВС║АД) ВС=10см ;АД= 2дм; Высота5см.Найдите площадь трапеции. ( Решают устно по готовому чертежу: Sтрап. =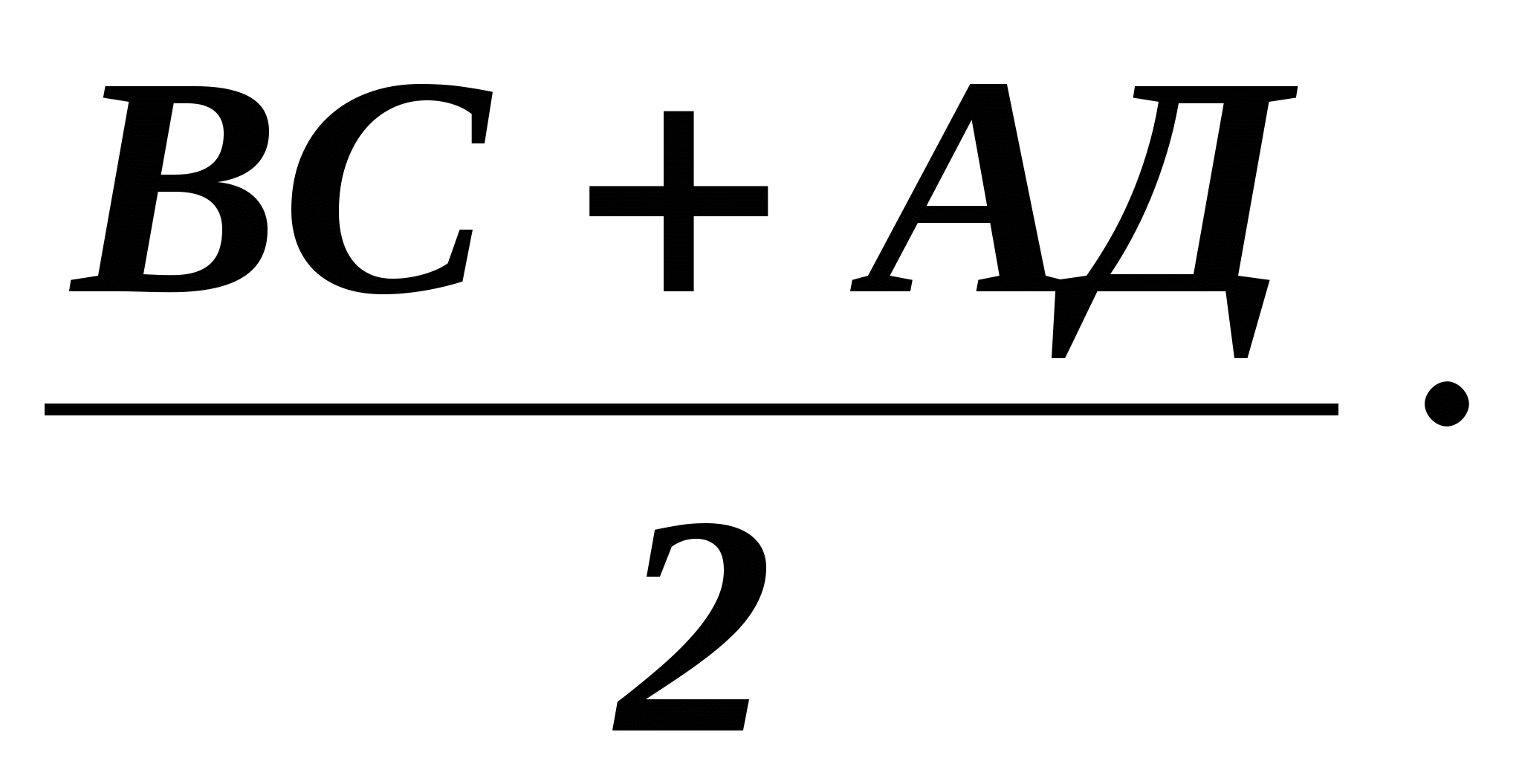h = =75см2) 2.Средняя линия трапеции равна 10 см , а высота 5см. Найдите площадь трапеции. ( Решение на доске: Sтрап. =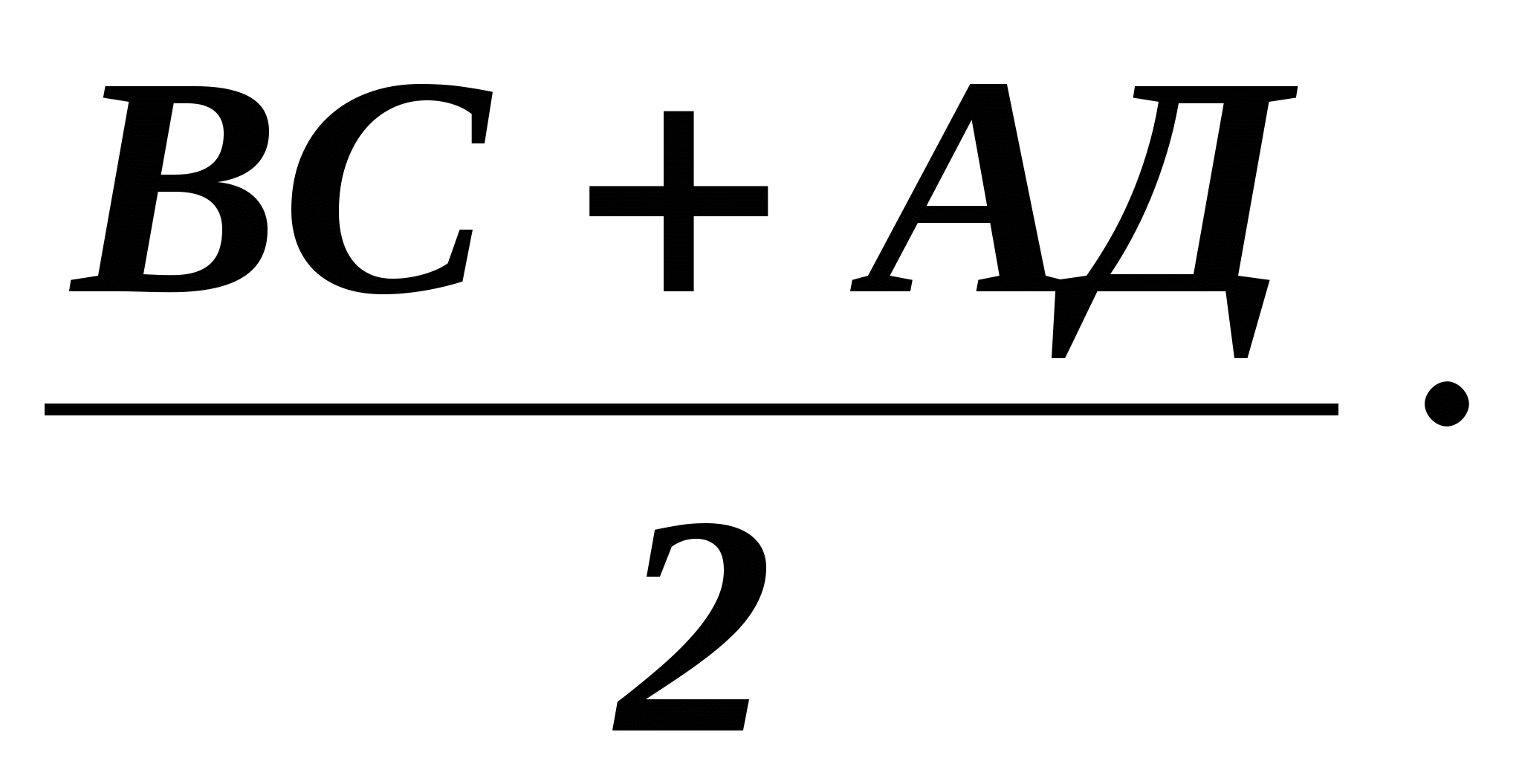h = 10∙5= 50см2 3.Решение задач по готовым чертежам: (решают устно в парах , записи проводят на черновиках) 1. 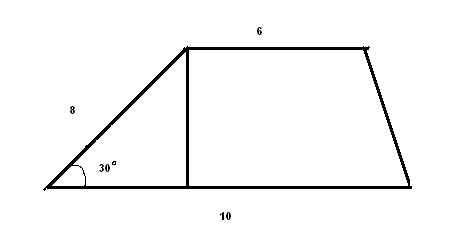2. 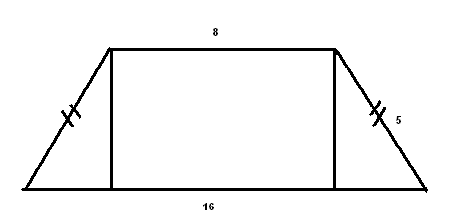3. 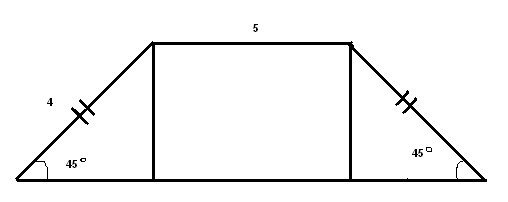Ответы к задачам по готовым чертежам: 1.Sтрап. =(10+6)∙4: 2 = 32(ед2)( высота равна половине гипотенузы из прямоугольного треугольника с углом 30) 2.найдём сначала высоту: противолежащий катет равен произведению гипотенузы и синуса угла в 45, т.е.4·=2, Sтрап.=(5+4)∙: 2=5(ед2) 3.Найдём высоту по теореме Пифагора из прямоугольного треугольника h = =; Sтрап.=(8+14) : 2·4=44(ед2) IV.Об истории понятия площади.(Сообщение делают ученики) 1.«Начальные геометрические сведения дошли до нас из глубокой древности. Первоначальные геометрические знания были получены опытным путём. А получение новых геометрических фактов при помощи рассуждений – доказательств началось с древнегреческого учёного Фалеса (6 век до нашей эры). Он установил свойства равнобедренного треугольника, свойства вертикальных углов, угла, опирающегося на диаметр окружности и т. д. Пифагор, соотечественник Фалеса и живший с ним в одном и том же веке, доказал знаменитое свойство гипотенузы прямоугольного треугольника. В 4 веке до н.э. жили и создавали геометрическую науку Евдокс и Теэтет.В 3 веке до н.э. древнегреческий учёный Евклид написал знаменитую книгу «Начала». В этой книге Евклид систематизировал накопленные к тому времени геометрические знания и попытался дать законченное аксиоматическое изложение этой науки. Написан этот труд был настолько замечательно , что в течение 2000 лет по всему миру преподавание велось либо по переводам , либо по незначительно переработанным книгам Евклида. О самом ученом сохранились очень скудные сведения. До наших времён дошли лишь сведения о том, что он преподавал в Александрии , столице царя Птолемея, который царствовал с 306 по 283 год до н.э. Формулы для вычисления площадей земельных участков, имеющих формы прямоугольников, треугольников , трапеций приведены в клинописных таблицах Древнего Вавилона , относящихся к 2000 году до н.э.. И , если вести хотя бы приближённый учёт времени возникновения понятия площади , то получится более 4000 лет. 2.Об измерении площадей в России. Рукописи, дошедшие до нас из глубины веков, говорят о том , что уровень знаний науки «геометрии» на Руси до начала 16 века был невысок. Так известно , что в 1551 году царь Иван IV решил впервые послать «смерить государство».Вероятно было известно по каким правилам надо было проводить измерения земельных угодий государства Российского и имелись люди , знающие геометрию. Но, первая книга , где излагаются правила измерения площадей , была книга «сошного письма», относящаяся к 1629 году. В те далёкие времена также , как и мы в настоящее время ,измеряемые участки сложной формы разбивали на более простые- на треугольники , прямоугольники, квадраты , трапеции. Площадь прямоугольника , квадрата измеряли верно, а вот площади треугольника , трапеции вычисляли с ошибками. Так , площадь треугольника измеряли как половину от произведения меньшей стороны на большую, а площадь равнобедренной трапеции принималась равной произведению полусуммы оснований на длину боковой стороны. В Старинных русских рукописях содержатся ошибки в способах измерения площадей, также там утверждалось , что фигуры с равными периметрами замыкают равные площади, что тоже неверно. А может быть в рукописях допущены ошибки переписчиками?. И всё же трудно верить в невысокий уровень знаний геометрии на Руси, когда в 1553-1560 годах при Иване Грозном выстроен собор Василия Блаженного «мастерами каменных дел Посником , Яковлевым и Бармой. Невозможно представить себе , что создание такого архитектурного шедевра могло обойтись без широких геометрических знаний. Конечно, трудно поверить , но до конца XVвека в России математические книги были запрещены как «богомерзостные» . И только в 1701 году Пётр I основал в Москве школу «Математических и навигатских наук» , где впервые были введены арифметика , алгебра , геометрия и тригонометрия, и вскоре были переведены на русский язык и изданы «начала» Евклида под редакцией англичанина Форварсьна. V.Формула Герона для равнобедренной трапеции.( сообщение делает либо учитель , либо хорошо подготовленный ученик) Для треугольника справедлива формула Герона: S=, где p –полупериметр треугольника, a,b,с – стороны треугольника. Интересна попытка индийского учёного Брамагупты (595-660г.г.)получить подобную формулу для измерения площади четырёхугольника. Если мы обозначим площадь четырёхугольника через S, p- его полупериметр ,a, b.с- стороны,то S трап.= Формула Брамагупты верна для прямоугольника . Тогда как b=d,a=c, то получим S=2 =(p-a) (p-b), но p-a=b,p-b=a, следовательно S=a. Формула Брамагупты остаётся верной и для равнобокой трапеции: В самом деле :S=так как a=c, то S==(p-a). Доказательство: S=(p-a) == =(p-a). По условию боковые стороны равны , следовательно , имеем из прямоугольного треугольника h=, а это означает , что S=(p-a)=== V.Практическая работа(выполняется в парах) 1. В тетради соседа по парте начертить трапецию, обменять тетради. 2.Выполнить необходимые измерения и по формуле найти площадь трапеции, 3. Выполнить взаимопроверку в парах. 4.По заранее заготовленным учителем моделям трапеции выполнить необходимые измерения и вычислить её площадь. VI.Работа с учебником Решение задач : №40 и №39 №40 Решение задачи полностью приведено в учебнике на странице221. Решить её удоски. №39.(решение выполняется учащимся у доски) 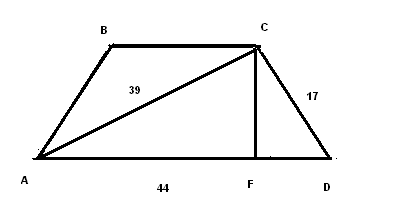Дано: АВСД- равнобокая трапеция , АД= 44см, СД=17см,АС=39см, АС-диагональ Найти: SABCD Решение: SABCD= Высоту CF найдём из площади треугольника АСД, SACD===330см2 h=CF===15см2 По условию трапеция равнобедренная ВС=АС-2FD=44-2=28см. FDнайдём из прямоугольного треугольникаCFD: FD== SABCD== Можно предложить вторым способом по формуле Брахмагупта: p=,S== =36=540cм2 VII.Подведение итога урока: 1.Как находится площадь трапеции? 2.Можно ли её применить для площади параллелограмма, для площади треугольника, для площади квадрата? VIII.Домашнее задание: Задачи №37, №38 , п.126. IX.Математический софизм :64=65!