Математическое моделирование. Имитационные модели
 Скачать 105.64 Kb. Скачать 105.64 Kb.
|
| Урок Тема: Математическое моделирование. Имитационные модели Цели:
Ход урока I. Организационный момент. Ход урока: II Актуализация знаний. В форме фронтального опроса: 1. Что такое деловая графика? 2. Какой вид имеет условная функция? Как она выполняется? 3. Как в электронной таблице реализуются логические операции при записи условных функций? 4. Что такое абсолютный адрес? III Теоретическая часть. Работа с учебником ( стр 125-131) с использованием демонстрационного материала Цор Математическая модель Что такое компьютерное математическое моделирование? Реальную систему, для которой создается математическая модель, принято называть объектом моделирования. Объектами математического моделирования могут быть некоторые конструкции, например, железнодорожный мост или корабль; природные объекты, например месторождение полезных ископаемых, водохранилище, а также процессы и явления, происходящие во времени, например взлет космической ракеты с космодрома, изменение погодных условий в определенной географической точке, изменение со временем численности определенных популяций. Для людей могут оказаться жизненно важными многие вопросы, связанные с этими объектами и процессами. Например: на какой высоте ракета достигнет первой космической скорости и выйдет на орбиту спутника Земли; до какой предельной температуры нагреется ее оболочка? Какой может быть максимальная нагрузка на железнодорожный мост, при которой не будет происходить его разрушение? Каким будет уровень воды в водохранилище в тех погодных условиях, которые предсказывают метеорологи? Не вымрет ли данная популяция животных через сто лет? На эти вопросы желательно получить ответы теоретическим путем, поскольку экспериментальный путь либо не-возможен, либо он возможен, но опасен. Например, при перегрузке моста можно его разрушить, при перегреве корпуса ракеты ее можно сжечь; а экспериментально проверить, что будет с популяцией животных через сто лет, невозможно. В подобных ситуациях на помощь человеку приходят математическое моделирование и вычислительный эксперимент. Этапы математического моделирования В математической модели используются количественные (числовые) характеристики объекта. Например, в математической модели полета ракеты учитываются масса и скорость ракеты, сила тяги двигателей, сопротивление атмосферного воздуха, теплоемкость обшивки ракеты, время полета, высота ракеты над поверхностью Земли, плотность атмосферы. Все эти величины связываются между собой через уравнения, отражающие физические законы движения тела в воздушной среде, нагревания тела в процессе трения. Из этих уравнений, зная одни величины — исходные данные, можно вычислить другие величины — результаты. Например, зная массу ракеты, силу тяги двигателей, скорость сгорания топлива, коэффициент трения воздуха о корпус, можно вычислить, какой будет высота и скорость ракеты в данный момент времени, а также температура обшивки ракеты. Часто такие расчеты бывает трудно осуществить вручную, и тогда используются компьютерные методы решения задачи. Реализованная на компьютере математическая модель называется компьютерной математической моделью, а проведение расчетов с помощью компьютерной модели с целью прогнозирования поведения моделируемой системы называется вычислительным экспериментом. Таким образом, этапы компьютерного математического моделирования следующие: 1) выделение количественных характеристик моделируемой системы, существенных для решаемой задачи; 2) получение математических соотношений (формул, уравнений, систем уравнений и пр.), связывающих эти характеристики; 3) определение способа решения полученной математической задачи и реализация ее на компьютере с помощью прикладных программных средств или на языках программирования; 4) решение поставленной задачи путем проведения вычислительного эксперимента. В результате вычислительного эксперимента можно получить прогноз поведения исследуемой системы; выяснить вопрос о том, как изменение одних характеристик системы отразится на других. Одним из видов прикладных программных средств, пригодных для реализации математической модели на компьютере, являются электронные таблицы.  Пример математического моделирования в ЭТ Чаще всего электронные таблицы используются в задачах для получения расчетных ведомостей, смет, справок, списков, т. е. в области делопроизводства. Однако электронные таблицы могут оказаться полезными и для научных целей. С их помощью можно строить компьютерные математические модели, проводить вычислительные эксперименты. Рассмотрим пример такого вычислительного эксперимента. Ученые установили, что прирост какого-либо вида живых организмов за счет рождаемости прямо пропорционален их количеству, а убыль за счет смертности прямо пропорциональна квадрату их количества. Этот закон известен под названием закона Мальтуса. Пусть в одном хозяйстве собираются разводить карпов. Прежде чем запускать мальков в пруд, решили провести расчеты. Согласно закону Мальтуса, изменение числа рыб за один год вычисляется по формуле N = kN – qN2 Здесь N — число карпов в начале года, k — коэффициент прироста, q — коэффициент смертности. Экспериментально установлено, что для данного вида рыб (карпы) и в данных условиях (состояние водоема, наличие корма) k = 1, q = 0,001. Если первоначально в пруд запущено N0 рыб, то из закона следует, что количество карпов через год будет таким: N1 = N0 + (kN0 – qN02) Через два года: N2 = N1 + (kN1 – qN12) и так далее. Можно написать общую формулу для вычисления количества рыб в 1-м году после их запуска: Ni = Ni-1 + (kNi-1 – qNi-12), i = 1, 2, 3… Эта формула является математической моделью процесса размножения рыб в водоеме. Заполним электронную таблицу для проведения по этой формуле расчета рыбного «поголовья» в пруду в течение нескольких лет:
Не надо думать, что всю таблицу приходится вводить посимвольно с клавиатуры. Строки, начиная с 7-й, формируются путем копирования предыдущей строки. При этом относительные адреса изменяются автоматически. Для получения результатов достаточно занести в ячейку F1 первоначальное число рыб. Теперь можно экспериментировать. Проследим, как за 10 лет будет меняться число карпов при разном количестве первоначально запущенных рыб. Вот несколько таблиц с результатами таких расчетов:
Из таблиц следует, что невозможно иметь в пруду 2000 карпов и более. Если начальное число рыб меньше 1000, то оно постепенно будет расти до 1000 штук и далее не будет меняться. Если сразу запустить 1000 рыб, то это количество останется неизменным и в последующие годы. Даже если запустить сначала 1500 рыб, то через год их численность в два раза сократится, а затем все равно дойдет до 1000. Если же запустить в пруд 2000 рыб, то через год все они вымрут. Из полученных результатов рыбоводы могут сделать практические выводы. Приведенные выше таблицы автоматически получались после изменений значения всего лишь в одной ячейке 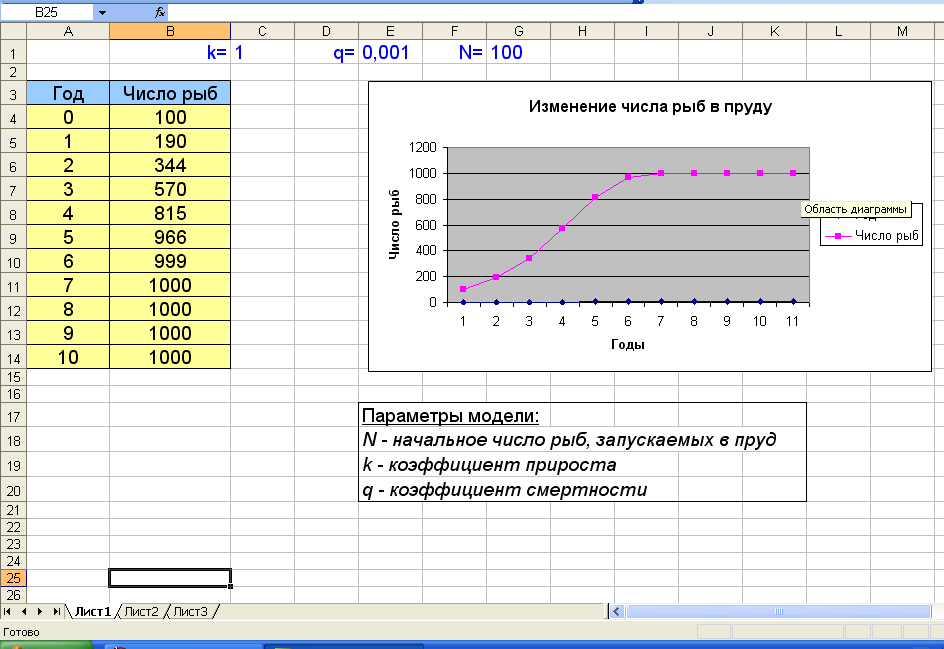 VI Практическая часть. (15 мин)
V Закрепление изученного материала. В форме фронтального опроса:
VI Домашнее задание. Изучить §23, 24. Кроссворд по теме «Электронные таблицы» . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||