|
Конспект урока по алгебре и началам математического анализа 10 класс тема урока «Преобразование графиков тригонометрических функций» Учитель математики: Ионова Е. В
Государственное бюджетное образовательное учреждение средняя общеобразовательная школа № 267
Конспект урока по алгебре и началам математического анализа
10 класс
тема урока «Преобразование графиков тригонометрических функций»
Учитель математики:
Ионова Е.В.
первая квалификационная категория
ГБОУ СОШ № 267,
СВАО, г. Москва.
Москва, 2013
Тема урока: Преобразование графиков тригонометрических функций.
Цель: Формирование представлений об изменении графиков тригонометрических функций в зависимости от изменения коэффициентов.
Задачи:
- рассмотреть влияние коэффициентов на поведение графика функции;
- актуализация знаний элементарных преобразований графиков функций;
- формирование навыка преобразования графиков тригонометрических функций;
- формирование умения строить графики тригонометрических функций путем сдвига, сжатия и растяжения шаблонного графика, относительно осей координат;
-развитие навыка построения графиков тригонометрических функций;
-формирование представления о связи между аккуратностью выполнения работы и результатом.
Тип урока: объяснение нового материала.
Место урока в теме: первый урок по теме.
Оборудование: интерактивный комплекс «PROMETHEAN», меловая доска, цветные карандаши.
ПО: GSP406_ru(живая геометрия).
Учебник: Алгебра и начала математического анализа. 10-11 классы: учеб. для общеобразоват. учреждений/ Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др.; под ред. А.Н.Колмогорова. – М.: Просвещение, 2010.
№
П.п.
|
Этапы урока, время
|
Деятельность учителя
|
Деятельность учащихся
|
Использование интерактивного комплекса, программ, ЭОР.
|
Использование меловой доски
|
1.
|
Организационный момент.
|
Приветствие. Проверка готовности к уроку. Наличие цветных карандашей, линейки, ластика.
|
Активизация комплекса. Открытие чистого листа в ЖГ(живая геометрия)
|
|
2.
|
Актуализация ранее изученного (фронтальный опрос).
|
- Что такое функция?
- Как задается функция?
- Что такое график функции?
-Какой график называется шаблонным?
- Приведите примеры функций. Назовите их.
- Какие из названных Вами функций являются периодическими? Что означает «периодическая функция»?
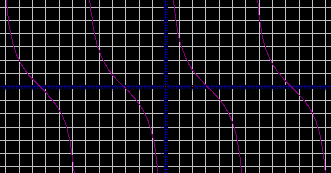
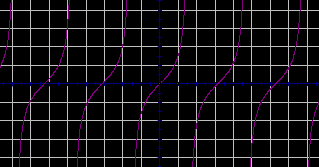
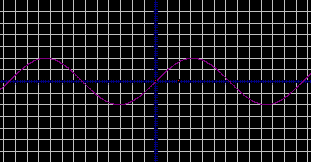
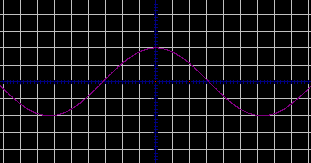
Посмотрите на доску и определите, график какой функции построен? Как называется соответствующая линия?
|
- функция, зависимость одной переменной от другой. Х-независимая переменная, У-зависимая переменная.
- функция задается уравнением, которое задает зависимость.
- график функции – это множество точек на координатной плоскости, подставив координаты которых в уравнение задающее функцию получится верное равенство.
- шаблонным называется график, который задается уравнением с коэффициентами равными 1 и 0(в зависимости от положения коэффициента в уравнении).
- у=3х+2 линейная функция
- у=5х2+3х+7 квадратичная функция
- у=sin x, y=cos x, y=tg x, y=ctg x – тригонометрические функции.
- тригонометрические функции являются периодическими. Период – это повторение значений функции «У» через определенный промежуток значений «Х».
- котангенс, график котангенсоида.
- тангенс, тангенсоида.
- синус, синусоида.
- косинус, косинусоида.
|
|
|
3.
|
Изучение нового материала.
|
В любом уравнении присутствуют коэффициенты, обозначить мы их можем разными буквами. Рассмотрим влияние коэффициентов на график функции.
Обратите внимание, что формула, которую мы составили в начале, внеся в нее коэффициенты, содержит в скобках «-». Значит если мы берем положительное значение, знак «-» сохраняется, если отрицательное, то знак меняется.
|
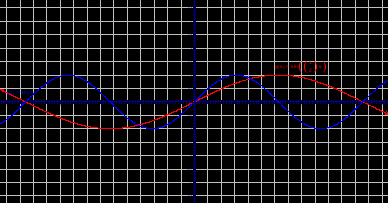
Записывают в тетрадь, при каком коэффициенте как меняется график функции.
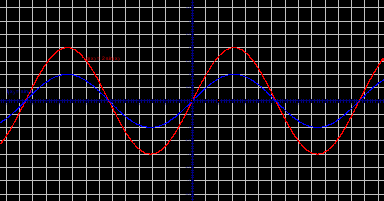
k>1, график вытягивается вдоль оси ОУ.
0
k<0, график переворачивается относительно оси ОХ.
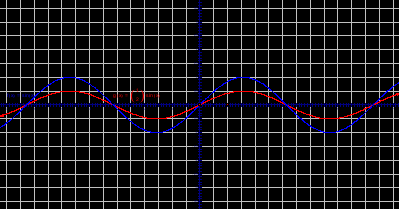
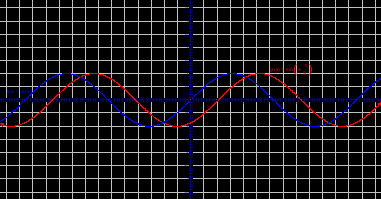
n>1, график сжимается вдоль оси ОХ. Меняется период функции.
0
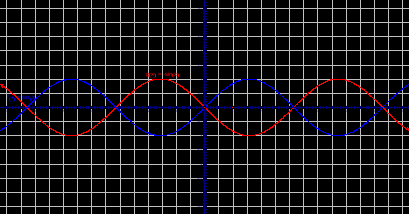
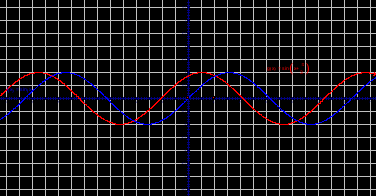
m>0, график сдвигается в положительном направлении по оси ОХ.
m<0, график функции сдвигается в отрицательном направлении по оси ОХ.
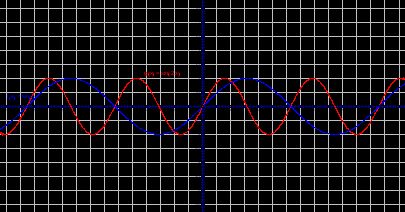
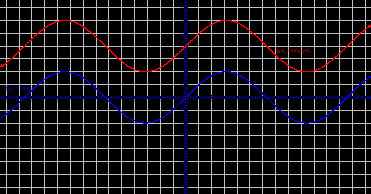
b>0, график функции сдвигается вверх по оси ОУ.
b<0, график функции сдвигается вниз по оси ОУ.
|
|
y=k sin (nx-m)+b
y=2sin x
y=1/2 sin x
y= - sin x
y=sin (2x)
y=sin( ½ x)
y=sin (x – π/3)
y=sin (x + π/3)
y=sin (x) + 2
y=sin (x) - 2
|
4.
|
Первичное закрепление
|
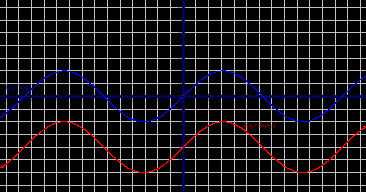
Самостоятельная работа. Определить по графику как изменились коэффициенты для y=cos x. (приложение №1)
|
|
|
|
Рефлексия.
|
Проверка самостоятельной работы при помощи программы ЖГ.
|
5.
|
Подведение итогов
|
Зависит ли воздействие коэффициентов на график функции от самой функции?
Влияет ли последовательность применения коэффициентов на график функции?
Как может изменяться график функции, и какой коэффициент за это отвечает?
|
Нет, коэффициенты ведут себя одинаково во всех случаях. Будь то квадратичная, линейная или тригонометрическая функция. Изменения графика относительно осей координат зависят только от соответствующих коэффициентов.
Нет. Действие каждого коэффициента не зависит от другого.
- k, растяжение и сжатие вдоль оси ОУ.
- n, растяжение и сжатие вдоль оси ОХ.
- m, перемещение влево или вправо по оси ОХ.
- b, перемещение вверх или вниз по оси ОУ.
|
|
y=k sin (nx-m)+b
|
6.
|
Домашнее задание
|
1.Попробуйте дома построить график данной функции путем сдвигов, сжатия и растяжения.
2. тест № 2 на Семинфо ФГОС.
Всего хорошего. Урок окончен.
|
|
|
y=1/2 cos (2x-π/2)+1
| |
|
|
 Скачать 73.69 Kb.
Скачать 73.69 Kb.











