Конкурсное задание «Методический семинар»
 Скачать 164.27 Kb. Скачать 164.27 Kb.
|
| «Учитель года города Ишима – 2015» Конкурсное задание «Методический семинар» Игровые технологии как средство формирования познавательного интереса на уроках математики в условиях ФГОС. Особенность федеральных государственных образовательных стандартов общего образования - их деятельностный характер, который ставит главной задачей развитие личности ученика. Современное образование отказывается от традиционного представления результатов обучения в виде знаний, умений и навыков; формулировки ФГОС указывают на реальные виды деятельности. Поставленная задача требует внедрение в современную школу системно-деятельностного подхода к организации образовательного процесса, который, в свою очередь, связан с принципиальными изменениями деятельности учителя, реализующего новый стандарт. Также изменяются и технологии обучения. Что же такое педагогическая технология? • Совокупность приёмов – область педагогического знания, отражающего характеристики глубинных процессов педагогической деятельности, особенности их взаимодействия, управление которыми обеспечивает необходимую эффективность учебно-воспитательного процесса; • Совокупность форм, методов, приёмов и средств передачи социального опыта, а также техническое оснащение этого процесса; • Совокупность способов организации учебно-познавательного процесса или последовательность определённых действий, операций, связанных с конкретной деятельностью учителя и направленных на достижение поставленных целей (технологическая цепочка). В этих условиях традиционная школа, реализующая классическую модель образования, стала непродуктивной. Передо мной, как и перед моими коллегами, возникла проблема – превратить традиционное обучение, направленное на накопление знаний, умений, навыков, в процесс развития личности ребенка. Уход от традиционного урока через использование в процессе обучения новых технологий позволяет устранить однообразие образовательной среды и монотонность учебного процесса, создаст условия для смены видов деятельности обучающихся, позволит реализовать принципы здоровьесбережения. Рекомендуется осуществлять выбор технологии в зависимости от предметного содержания, целей урока, уровня подготовленности обучающихся, возможности удовлетворения их образовательных запросов, возрастной категории обучающихся. В условиях реализации требований ФГОС одной из наиболее актуальных технологий становится игровая технология. Активность и интерес к деятельности зависит от характера деятельности и ее организации. Известно, что деятельность, в которой ставятся вопросы, проблемы, требующие самостоятельного решения, деятельность, в процессе которой рождаются положительные эмоции (радость успеха, удовлетворения и др.), чаще всего вызывают интерес, активную познавательную деятельность. И наоборот, деятельность однообразная, рассчитанная на механическое выполнение, запоминание, как правило, не может вызвать интереса, отсутствие положительных эмоций может привести к пассивности. Математические игры разнообразны, требуют самостоятельности и эмоционально насыщены. Использование их на внеклассных занятиях повышает активность учащихся, заряжает положительными эмоциями, способствует возникновению познавательного интереса к предмету. Математическая игра завлекает учащихся. Они с увлечением выполняют различные задания. Учащиеся не задумываются над тем, что во время игры они учатся, занимаются тем же умственным трудом, что и на уроках. Все это говорит о том, что математическую игру нужно использовать во внеклассной работе по математике для того чтобы воздействовать на пробуждение интеллектуальной активности школьников и формирование у них интереса к предмету. Цели, задачи, функции, требования математической игры Основная цель применения математической игры на внеклассных занятиях по математике – это развитие устойчивого познавательного интереса у учащихся к предмету через разнообразие используемых математических игр. Так же можно выделить и следующие цели применения математических игр:
Математические игры призваны решать следующие задачи.
Виды математических игр Одним из требований к математическим играм является их многообразие. Можно привести следующую классификацию математических игр по разным основаниям, но она не будет являться строгой, так как каждую игру можно отнести к нескольким видам из этой классификации. Итак, система математических игр включает следующие виды: По назначению различают обучающие, контролирующие, обобщающие и воспитывающие игры. Также можно выделить развивающие и занимательные. По массовости различают коллективные и индивидуальные игры. По реакции выделяют подвижные и тихие игры. По темпу выделяют скоростные и качественные игры. Некоторые математические игры должны принимать форму состязаний, соревнований между командами или на личное первенство, это обусловлено характерной чертой подростков, стремления к различным видам состязаний. Наконец, различают игры одиночные и универсальные. К одиночным играм относят те игры, правила которых не допускают изменения содержания игры, они разработаны с учетом особенностей конкретного материала. Универсальные игры же, наоборот, позволяют менять свое содержание. Они разрабатываются по широкому кругу вопросов школьной программы, могут использоваться в различных целях, на различных внеклассных мероприятиях, и поэтому являются очень ценными. Приведем еще одну классификацию игр по схожести правил и характера проведения. Данная классификация будет включать в себя следующие виды игр:
Выше перечисленные виды игр могут переплетаться, игра может сочетать в себе элементы разных игр. В связи с этим, на практике наблюдается многообразие математических игр. Проведение внеклассных занятий в форме математических игр позволит их разнообразить, привлечь к ним разные группы учащихся: интересующихся математикой, не проявляющих явного интереса, слабых, сильных и т.п. Правильно выбранный вид математической игры с учетом возраста и типа учащихся способствует привлечению большего числа школьников к внеклассной работе по математике, возникновения у них интереса к предмету. Структура математической игры Математическая игра имеет устойчивую структуру, которая отличает ее от всякой другой деятельности. Основными структурными компонентами математической игры являются: игровой замысел, правила, игровые действия, содержание, оборудование, результат игры. Сочетание всех элементов игры и их взаимодействие повышают организованность игры, ее эффективность, приводит к желаемому результату. Такая игра способствует возникновению желания участвовать в ней, пробуждает положительное отношение к ней, повышает познавательную активность и интерес. Организационные этапы математической игры Для того чтобы провести математическую игру, и ее результаты были бы положительными, необходимо провести ряд последовательных действий по ее организации. К организации математической игры относят ряд этапов. Каждый этап как часть единого целого включает определенную логику действий педагога и учащихся. Первый этап – это предварительная работа. На этом этапе происходит выбор самой игры, постановка цели, разработка программы ее проведения. Второй этап – подготовительный. В зависимости от того или иного вида игры этот этап может отличаться по времени и содержанию. Но все-таки у них есть общие черты. Во время подготовительного этапа учащиеся знакомятся с правилами игры, происходит психологический настрой на игру. Учитель организует детей. Подготовительный этап игры может проходить как непосредственно перед самой игрой, так и начаться заблаговременно до проведения самой игры. Третий этап – это непосредственно сама игра, воплощение программы в деятельности, реализация функций каждым участником игры. Содержание данного этапа зависит от того, какая игра проводиться. Четвертый этап – это заключительный этап или этап подведения итогов игры. Данный этап является обязательным, так как без него игра будет не полной, не законченной, потеряет смысл. Как правило, на этом этапе определяются победители, происходит их награждение. Так же на нем подводятся общие итоги игры: как прошла игра, понравилась ли она учащимся, нужно ли еще проводить подобные игры и т.п. Наличие всех этих этапов, их четкая продуманность делают игру целостной, завершенной, игра производит наибольший положительный эффект на учащихся, достигается цель – заинтересовать школьников математикой. Требования к подбору задач Любая математическая игра предполагает наличие задач, которые должны решить школьники, участвующие в игре. А каковы требования к их подбору? У разных видов игр они различны. Если взять математические мини-игры, то задачи входящие в них могут быть как по какой-нибудь теме школьной программы, так и необычные задачи, оригинальные, с увлекательной формулировкой. Чаще всего они бывают однотипные, на применение формул, правил, теорем, отличающиеся лишь по уровню сложности. Задачи для викторины должны быть с легко обозримым содержанием, не громоздкие, не требующие сколько-нибудь значительных выкладок или записей, в большинстве своем доступные для решения в уме. В играх по станциям, задачи на каждой станции должны быть однотипными, возможно использование задач не только на знание материала предмета математики, но и задания, не требующие глубоких математических знаний (например, спеть как можно больше песен, в тексте которых присутствуют числа). К задачам математических конкурсов и КВНов предъявляются следующие требования: они должны быть оригинальными, с простой и увлекательной формулировкой; решение задач не должно быть громоздким, требующим долгих вычислений, могут предполагать несколько решений; должны быть разными по уровню сложности и содержать материал не только школьной программы по математике. Для игр-путешествий отбираются легкие задачи, доступные для решения учащимися, в основном по программному материалу, не требующие больших вычислений. Можно использовать задачи занимательного характера. Если игра планируется проводиться для слабых учеников, не проявляющих интереса к математике, то лучше всего подобрать такие задачи, которые не требуют хороших знаний по предмету. Так же в игры можно включать задачи исторического характера, на знание каких-нибудь необычных фактов из истории математике, практического значения. В лабиринтах обычно используются задания на знание материала любого из разделов курса школьной математики. Трудность таких задач увеличивается по мере продвижения по лабиринту: чем ближе к концу, тем сложнее задача. В «математической карусели» и математических боях обычно используются задачи повышенной трудности, на глубокое знание материала, нестандартность мышления, так как для их решения отводится достаточно много времени и в таких играх участвуют в основном только сильные ученики. Учитывая все требования, возраст и тип учеников можно разработать такую игру, что она будет интересна всем участника. На уроках дети решают достаточно много задач, все они одинаковые и не интересные. Придя на математическую игру, они увидят, что решать задачи совсем не скучно, они бывают не такие сложные или наоборот однообразные, что у задач могут быть необычные и занятные формулировки, и не менее занятные решения. Решая задачи практического значения, они осознают всю значимость математики как науки. В свою очередь игровая форма, в которой будет проходить решение задач, придаст всему мероприятию совсем не учебный, а занимательный характер и дети не заметят, что они учатся. Требования к проведению математической игры Соблюдение всех требований к проведению математической игры способствует тому, что внеклассное мероприятие по математике пройдет на высоком уровне, оно понравится детям, будут достигнуты все поставленные цели. Учителю во время игры должна принадлежать ведущая роль в ее проведении. Учитель должен следить за порядком на игре. Отступление от правил, терпимость к мелким шалостям или дисциплины, в конечном счете, могут привести к срыву занятия. Математическая игра будет не только не полезной, она принесет вред. Учитель является еще и организатором игры. Игра должна быть четко организована, выделены все ее этапы, от этого зависит успех игры. Данному требованию следует придавать самое серьезное значение и иметь его в виду при проведении игры, особенно массовой. При проведении математической игры важно следить за сохранением интереса школьников к игре. При отсутствии интереса или угасании его ни в коем случае не следует принудительно навязывать игру детям, так как в этом случае она теряет свою добровольность, обучающее и развивающее значение, из игровой деятельности выпадает самое ценное – ее эмоциональное начало. При потере интереса к игре учителю следует принять действия, ведущие к изменению обстановки. Этому могут служить эмоциональная речь, приветливая обстановка, поддержка отстающих. Учитель сам должен в определенной степени включаться в игру, являться ее участником, иначе руководство и влияние его будут недостаточно естественными. Он должен положить начало творческой работе учащихся, умело ввести их в игру. Учащиеся должны понимать смысл и содержание всей игры, что сейчас происходит и что делать дальше. Все правила игры должны быть разъяснены участникам. Это происходит в основном на подготовительном этапе. Математическое содержание должно быть доступно пониманию школьников. Все препятствия должны быть преодолены, предлагаемые задания должны быть решены самими учащимися, а не учителем или его помощником. В противном случае игра не вызовет интереса и будет проводиться формально. Все участники игры должны активно участвовать в ней, заняты делом. Длительное ожидание своей очереди для включения в игру снижает интерес у детей к этой игре. Легкие и сложные конкурсы должны чередоваться. По содержанию она должна быть педагогична, зависеть от возраста и кругозора участников. В процессе игры учащиеся должны математически грамотно проводить свои рассуждения, математическая речь должна быть правильной. Во время проведения игры должен быть обеспечен контроль за результатами, со стороны всего коллектива учеников или выбранных лиц. Учет результатов должен быть открытым, ясным и справедливым. Ошибки в учете неясности в самой организации учета приводят к несправедливым выводам о победителях, а, следовательно, и к недовольству участников игры. Любая игра должна быть результативна. Результатом может быть победа, проигрыш, ничья. Только законченная игра, с подведенным итогом может сыграть положительную роль, произвести на учащихся благоприятное впечатление. Интересная игра, доставившая детям удовольствие, оказывает положительное влияние на проведение последующих математических игр, их посещение. При проведении математических игр забавность и обучение надо сочетать так, чтобы они не мешали, а наоборот помогали друг другу. Математическая сторона содержания игры всегда должна отчетливо выдвигаться на первый план. Только тогда игра будет выполнять свою роль в математическом развитии детей и воспитание интереса к математике. Это все основные требования, предъявляемые к проведению математической игры. Из всего сказанного выше можно сделать вывод, что математическую игру целесообразно применять на внеклассных занятиях по математике. Она вносит необычность во внеклассную работу по математике, многообразие ее видов позволяет разнообразить внеклассные занятия по математике, каждый раз удивлять учащихся новой формой и содержанием игры. Это все вызывает интерес у школьников. А чтобы математическая игра как можно больше способствовала развитию познавательного интереса, нужно при ее подготовке учитывать все требования к подбору задач и проведению самой игры, правильно выбрать тип игры и ее содержание. ВЫВОД Существуют различные подходы к определению понятия игры, но все они сходятся в одном, что игра является способом развития личности, обогащения ее жизненного опыта. Из всего многообразия игр можно выделить математическую игру, как средство развития познавательного интереса учащихся к математике. Использование математической игры во внеклассной работе по математике наиболее эффективно способствует возникновению интереса у учащихся к математике. Анкетирование учеников Для того, чтобы показать эффективность использования математической игры для развития познавательного интереса одного теоретического обоснования недостаточно. Любая теория должна быть подтверждена практикой. В связи с этим в школе № 7 города Ишима был проведен опрос среди учеников 5-11 классов. Всего в опросе участвовало 340 человек. Анкета включала в себя следующие вопросы:
Результаты анкетирования учащихся были следующими. На первый вопрос: «Проводились ли у вас когда-нибудь игры по математике?», все учащиеся ответили положительно. Это значит, что и в школе используется такая форма внеклассной работы как математическая игра, и дети в большинстве своем посещают такие мероприятия. Н  а второй же вопрос: «Нравится ли вам посещать такие мероприятия?», большинство учащихся ответили: «Да», а именно, 307 человека, что составляет 91% от всего количества опрашиваемых. Отрицательно ответили 12 человек, что составляет 4% от всех опрошенных. Остальные же 21 человек ответили: «Не знаю» (5 человек – 1%) и «В зависимости от того, какая игра» (16 человек – 5%). а второй же вопрос: «Нравится ли вам посещать такие мероприятия?», большинство учащихся ответили: «Да», а именно, 307 человека, что составляет 91% от всего количества опрашиваемых. Отрицательно ответили 12 человек, что составляет 4% от всех опрошенных. Остальные же 21 человек ответили: «Не знаю» (5 человек – 1%) и «В зависимости от того, какая игра» (16 человек – 5%).Следует заметить, что основной причиной отрицательного отношения к математическим играм является отрицательное отношение к самому предмету математике и к учебе в целом. Но таких учеников значительно меньше, по сравнению с остальными. Большинству учащихся в математической игре, проводимой для них, нравится все. Учащимся, которые, судя по всему, любят математику, нравится в математической игре то, что в ней по мере того, что весело и забавно, надо еще и думать. Наиболее значимым недостатком математической игры является дисциплина, шум и возможно плохая организация. Так же есть такие ответы как – несложные задания и трудные задачи. Поэтому при разработке математической игры учителю нужно продумывать задания, как для сильных, так и для слабых учащихся. И вообще, математическая игра должна быть продумана «до мелочей», чтобы во время ее проведения не возникало споров. Вопросы 4 и 5 являются наиболее значимыми. Учащиеся на них ответили следующим образом:  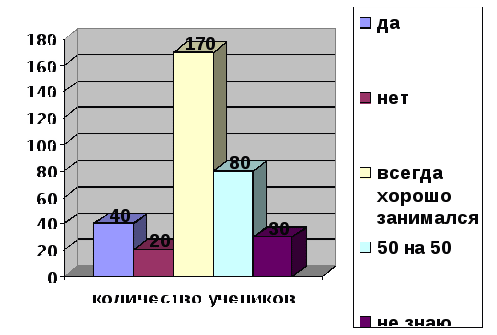 Как видно на диаграмме большинство учащихся после математической игры заинтересовались математикой, стали охотнее заниматься на уроках по этому предмету. На 6 вопрос: «Хотели бы вы еще поучаствовать в математической игре?» только 12 учеников ответили отрицательно из 340, 8 ответили, что не знают, 25 человека считают, что наверно и 295 человек с удовольствием бы посетили такое мероприятие еще раз. Это говорит о том, что внеклассные занятия, проводимые в форме математической игры, привлекают многих школьников. Учащиеся с удовольствием принимают в них участие, многие из них осознают и то, что таким необычным способом они узнают много нового, учатся. Благодаря таким мероприятиям в школе как математическая игра, математика открывается детям с другой стороны – оказывается, это не такой уж скучный предмет как им казалось. Ученики охотнее посещают не только внеклассные занятия, но и активнее работают на уроках математики. Итак, математическая игра отличается от других форм работы тем, что может дополнять другие формы работы по математике. А самое главное математическая игра дает возможность ученикам проявить себя, свои способности, проверить имеющиеся у них знания, приобрести новые знания, и все это в необычной занимательной форме. Систематическое использование математической игры в работе влечет за собой формирование и развития познавательного интереса у учащихся. Подводя итоги всего выше сказанного, считаю, что математическая игра, как эффективное средство развития познавательного интереса, должна использоваться во внеклассной работе и на уроках как можно чаще. Список литературы
|