Комбинаторика

Для успешной подготовки учащихся по этой теме, следует учитывать несколько факторов. Во-первых, на изучение программирования по базовому уровню отводится незначительное количество учебного времени. За это время они должны познакомиться с языком программирования, изучить основные операторы, научиться самостоятельно записывать несложные программы с использованием трех основных типов алгоритмических конструкций (линейных, ветвления и циклических) и уметь проводить их отладку. Во-вторых, невозможно одновременно учить комбинаторике и изучать один из языков программирования – это занимает много времени и не позволяет учащимся «видеть» задачу и пути ее решения.

Комбинаторика

• один из разделов дискретной математики, который приобрёл важное значение в связи с использованием его в теории вероятностей, математической логике, теории чисел, вычислительной технике и кибернетике, а также решений заданий ЕГЭ по математике и информатике

Принцип Дирихле

• Дирихле принцип (по имени П. Дирихле), принцип ящиков — предложение, утверждающее, что в случае m > n при отнесении каждого из m предметов к одному из n классов хотя бы в один класс попадёт не менее двух предметов. Это чрезвычайно простое предложение применяется при доказательстве многих важных теорем теории чисел, относящихся к приближению иррациональных чисел рациональными, в доказательствах трансцендентности чисел и других вопросах.

Решения 5 класс

• Можно!

• Т.к. сорта три, а ящиков 25, то возможны сочетания:

• 9+15+1,

• 9+14+2

• 9+13+3 и т.д.

План действия

• Для решения третьей задачи целесообразно записывать план действия, именно на ее примере следует вводить это понятие

• 8,0,0 →3,5,0→3,2,3→6,2,0→6,0,2→

• 1,5,2→1,4,3→4,4,0

• Вариант №2: 8,0,0→5,0,3→5,3,0→

• 2,3,3→2,5,1→7,0,1→7,1,0→4,1,3→4,4,0

Задача Люка

• Шашки расставлены в виде схемы. Требуется белые шашки поменять местами с черными, причем белые можно двигать только вправо, а черные – влево и любая шашка передвигатся либо на соседнюю пустую клетку, либо на пустую клетку, находящуюся непосредственно за ближайшей шашкой другого цвета

Принцип Дирихле ( 7или 8 класс)

• Шестеро друзей решили в один день побывать в 7 кинотеатрах, начало сеансов в которых в 9, 10…..18,19 часов. На каждый сеанс двое шли в один кинотеатр, остальные – в другой. Доказать, что в каждом из 7 кинотеатров хотя бы на одном сеансе в этот день не был ни один из друзей.

• Решение. 7-1= 6 друзей *на 11 сеансов (через каждый час по 1-му)=22 сеанса всего посетили. Если в 1-м из 7 кинотеатров они посетили все 11 сеансов, то в 6 остальных тоже посетили 11 сеансов, значит в каждом хотя бы на одном сеансе. Друзей всего 7, следовательно если брать по максимуму

• На 1-м сеансе – 2 друга,

• На втором – 2,

• (На третьем – 2), то в сумме получаем 6, т.е. кто-то их них в этом кинотетре не был.

Множества (8-9 класс)

• Определение множеств

• Сложение множеств (коммуникативный и ассоциативный закон)

• Пересечение множеств (дистрибутивный закон)

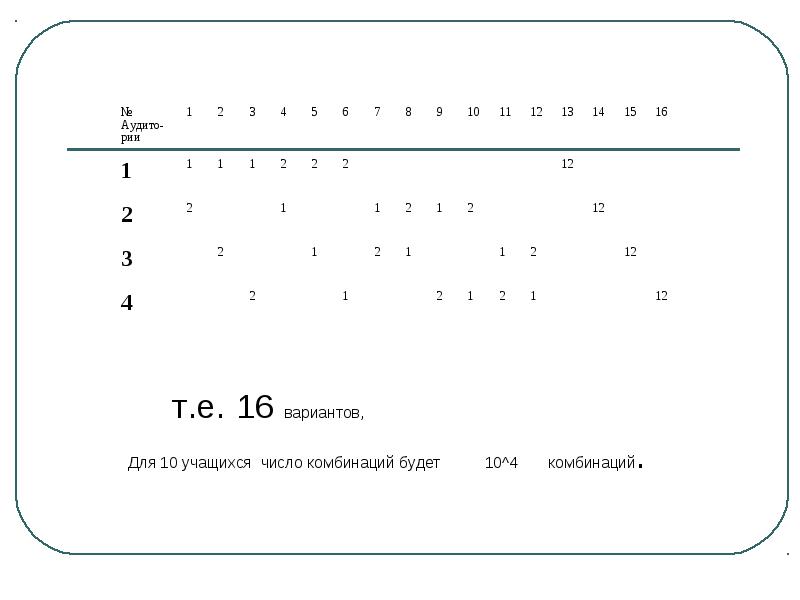
Комбинаторика

• Задачи дискретной математики, к которым относится большинство комбинаторных задач по информатике, часто сводятся к перебору различных комбинаторных конфигураций объектов и выбору среди них наилучшего, с точки зрения условия той или иной задачи. Поэтому знание алгоритмов генерации наиболее распространенных комбинаторных конфигураций является необходимым условием успешного решения таких задач в целом. Важно также знать количество различных вариантов для каждого типа комбинаторных конфигураций, так как это позволяет реально оценить вычислительную трудоемкость выбранного алгоритма решения той или иной задачи на перебор вариантов и, соответственно, его приемлемость для решения рассматриваемой задачи, с учетом ее размерности. Кроме того, при решении задач полезным оказывается умение для каждой из комбинаторных конфигураций выполнять следующие операции: по имеющейся конфигурации получать следующую за ней в лексикографическом порядке; определять номер данной конфигурации в лексикографической нумерации всех конфигураций; и, наоборот, по порядковому номеру выписывать соответствующую ему конфигурацию.