Из опыта работы учителя математики: «Как я учу детей решать уравнения с модулем»
 Скачать 137.81 Kb. Скачать 137.81 Kb.
|
       Из опыта работы учителя математики: Из опыта работы учителя математики:«Как я учу детей решать уравнения с модулем» Не секрет, что в настоящее время для успешной сдачи экзамена по математике недостаточно освоить программу в объеме общеобразовательной средней школы. Сложность задач, предлагаемых на экзаменах, постоянно возрастает. Для их решения требуется применять методы и приемы, знания которым в процессе обучения на уроках уделяется мало внимания. Существенной характеристикой числа, как в действительной, так и в комплексной области является понятие его абсолютной величины (модуля). Это понятие имеет широкое распространение в различных отделах физико-математических наук. Так, в математическом анализе одно из первых и фундаментальных понятий – понятие предела – в своем определении содержит понятие абсолютной величины числа. В теории приближенных вычислений первым, важнейшим понятием, является понятие абсолютной погрешности приближенного числа. В механике основным первоначальным понятием является понятие вектора, важнейшей характеристикой которого служит его абсолютная величина (модуль). Практически каждый учитель знает, какие проблемы вызывают у учащихся задания, содержащие модуль. Это один из самых трудных материалов, с которыми школьники сталкиваются на экзаменах. Несмотря на то, что тема «Модуль числа» проходит «красной нитью» через весь курс школьной и высшей математики, для ее изучения по программе отводится очень мало времени (в 6 классе -2 часа, в 8 классе - 4 часа). В то же время на ЕГЭ задачи с модулем предлагаются все чаще и чаще. Задачи, связанные с абсолютной величиной, часто встречаются и на математических олимпиадах. Несмотря на кажущуюся простоту определения модуля числа, решение уравнений и неравенств, содержащих неизвестные под знаком модуля, вызывает у учащихся определенные трудности. По-видимому, они связаны с тем, что решение задач подобного рода предполагает элементарные навыки исследования, логического мышления, заключающиеся в переборе различных возможных случаев, так как в подавляющем большинстве задач одно уравнение или неравенство с модулем равносильно совокупности или системе нескольких уравнений и неравенств, освобожденных от знака модуля. Исходя из всего вышесказанного, учителю необходимо использовать различные подходы и методы в обучении решению задач с модулем. Разнообразие методов будет способствовать сознательному усвоению математических знаний, вовлечению учащихся в творческую деятельность, а также решению ряда методических задач, встающих перед учителем в процессе обучения, в частности, реализации внутрипредметных связей (алгебра-геометрия), расширению области использования графиков, повышению графической культуры учеников. Наша задача – научить детей основным приемам решения задач с модулем. Учитывая свой опыт подготовки учащихся к экзаменам, осмелюсь утверждать, что обучать учеников решению уравнений с модулем можно и нужно уже в 7 классе при изучении таких тем, как «Линейное уравнение с одной переменной», «Линейная функция и её график», хотя еще раз отмечу, что, модули — трудная тема для учеников. Приступая к работе с ней, учитель должен понимать, что основные сложности учащиеся испытывают не при вычислении модуля, а при проведении алгебраических преобразований с ним. Я предлагаю Вашему вниманию наработанный материал и свою методику объяснения основного способа снятия модуля: разбора случаев по подмодульному выражению, которые я применяю на факультативных занятиях в 7 классе. Итак. Понятие модуля вводится в 6 классе. учащиеся уже знают: -положительные и отрицательные числа; -умеют отмечать эти числа на координатной прямой; -умеют находить числа, противоположные данным; -Понятие «модуль» водится как расстояние от начала координат до данной точки (геометрический смысл модуля). Модулем числа a называется расстояние в единичных отрезках от начала координат до точки А(а). Модуль числа не может быть отрицательным (расстояние не может быть отрицательным). Для положительного числа и нуля он равен самому числу, а для отрицательного – противоположному числу. Противоположные числа имеют равные модули: | -а | = а. Определение модуля как расстояние позволяет сформулировать следующее правило нахождения модуля действительного числа: -модуль положительного числа равен самому этому числу, -модуль нуля равен 0; -модуль отрицательного числа равен числу, противоположному данному, т.е. 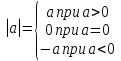 Это правило является классическим определением модуля действительного числа. В учебнике 7 класса (Алгебра 7 класс, Ю.Н.Макарычев, Н.Г. Миндюк и др.) задания с использование абсолютной величины встречаются нечасто, в основном, это задания повышенной сложности. № 219 Верно ли что для любых чисел a и b 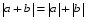 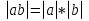 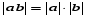 №220 Известно, что 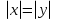 , верно ли, что х = у? , верно ли, что х = у? №221 Известно, что 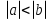 , верно ли, что а , верно ли, что а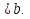 №222 Известно, что 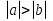 . Возможно ли, чтобы было а . Возможно ли, чтобы было а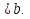 №225 Объясните, почему равенство является тождеством: 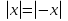 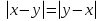 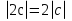 №226 Является ли тождеством равенство: 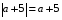 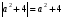 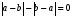 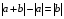 Мне такие задания позволяют углубить понимание абсолютной величины, а также дают возможность познакомить детей с некоторыми свойствами модуля: Модуль суммы двух чисел не больше суммы модулей этих чисел 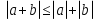 Модуль разности двух чисел не меньше разности модулей этих чисел 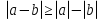 Модуль произведения двух чисел равен произведению модулей этих чисел 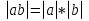 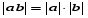 Модуль частного двух чисел равен частному модулей этих чисел 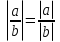 , b , b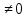 Модуль разности двух чисел равен расстоянию между точками числовой прямой, изображающими эти числа 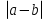  Из этого свойства следует важное равенство 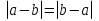 В частности, 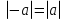 . .Покажу, в каких темах 7 класса я обучаю детей решению задач с модулем. В теме «Сравнение выражений» они знакомятся со строгими и нестрогими неравенствами, учатся работать с двойными неравенствами, поэтому я ввожу задания 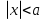 и и 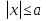 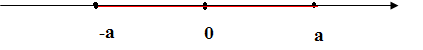 - а < х < а и 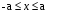 И, конечно, вспоминаем неравенства вида 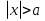 и и 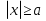 . .Покажу, как я учу детей раскрывать понятие модуля в выражении: например, 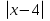 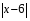 . .Выражение х - 6 обращается в 0 при х = 6. Разобьем числовую прямую на 2 луча х < 6 и х > 6 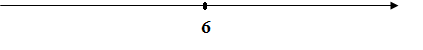 При 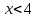 х < 6 выражение х – 6< 0 х < 6 выражение х – 6< 0 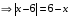 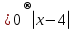 При x 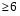 выражение х – 6 выражение х – 6 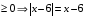 . .Обычно это записывают так: 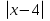 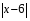 = = 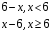 В дальнейшем я учу детей раскрывать модуль в выражении, содержащем несколько модулей например, 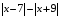 . .Решение: Выражения х - 7 и х + 9 обращаются в 0 при х = 7 и х = - 9 соответственно. Разобьем числовую прямую точками - 9 и 7 на три промежутка:  Чтобы было удобнее раскрывать модуль, знаки выражений х - 7 и х + 9 запишем в таблицу:
В первой строке таблицы указываем числовые промежутки, на которые точки х = 7 и х = - 9 разбивают числовую прямую. Расставляем знаки в строках таблицы. Выбираем произвольное значение х из рассматриваемого промежутка, подставляем его в выражение и определяем знак выражения. Если меньше 0, то ставим знак « », если больше 0, то знак «». Значения х из соответствующих промежутков выбираем произвольно, но так, чтобы было удобно вычислять. Полезно показать учащимся и другой способ записи данного этапа решения - когда знаки подмодульных выражений заносятся не в таблицу, а сразу непосредственно наносятся на числовую прямую (соответственно). В дальнейшем это упростит процесс решения уравнений такого вида, даст наглядное представление о выполняемой ими процедуре и научит контролировать несколько числовых потоков одновременно, хотя этот контроль и имеет многоэтапный, даже виртуальный характер, без участия в нем самих чисел. 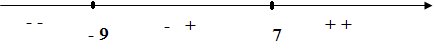 После того, как знаки в таблице (на числовой прямой) расставлены, пользуемся классическим определением модуля: при х < -9 получаем: - ( х – 7)+( х + 9) = - х + 7 + х + 9 = 16 при 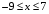 получаем: получаем:- ( х – 7)-( х + 9) = - х + 7 - х – 9 = -2 х – 2 при х > 7получаем: ( х – 7)-( х + 9) = х - 7 - х – 9 = -16 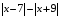 = = 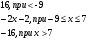 Такой метод раскрытия модулей носит название «метод интервалов». В теме «Линейные уравнения с одной переменной» я приступаю к решению уравнений. Вспомним основные понятия, используемые в данной теме. Уравнением с одной переменной называют равенство, содержащее переменную. Корнями уравнения называются значения переменной, при которых уравнение обращается в верное равенство. Решить уравнение – значит, найти все его корни или доказать, что корней нет. Уравнением с модулем называют равенство, содержащее переменную под знаком модуля. В учебнике математики есть задания с которых целесообразно начать первое занятие по данной теме: № 236 Почему не имеет корней уравнение: а) 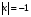 б) б) 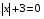 ? ?№237 Решите уравнение: а) 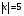 б) б) 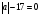 . .Задания такого уровня мы обычно разбираем устно. Далее переходим к более сложным уравнениям. При решении уравнений, содержащих знак абсолютной величины, мы будем основываться на определении модуля числа и свойствах абсолютной величины числа. Существует несколько способов решения уравнений с модулем. Рассмотрим подробнее некоторые из них. |а|=а, если а ≥ 0; |а|=-а, если а < 0. Метод последовательного раскрытия модуля. Опорная информация: Пример 1: Решим уравнение |х-5|=4. Исходя из определения модуля, произведем следующие рассуждения.
Решая полученные уравнения, находим: х1=9, х2=1. Ответ: 9; 1. Решим этим же способом уравнение, содержащее «модуль в модуле». Пример 2: Решим уравнение ||2х-1|-4|=6. Рассуждая аналогично, рассмотрим два случая. 1). |2х-1|-4=6, |2х-1|=10. Используя еще раз определение модуля, получим: 2х-1=10 либо 2х-1= -10. Откуда х1=5,5, х2= -4,5. 2). |2х-1|-4= -6, |2х-1|= -2. Понятно, что в этом случае уравнение не имеет решений, так как по определению модуль всегда неотрицателен. Ответ: 5,5; -4,5. Метод интервалов. |а| = а, если а ≥ 0; |а| = -а, если а < 0. Опорная информация: Метод интервалов – это метод разбиения числовой прямой на промежутки, в которых по определению модуля знак абсолютной величины можно будет снять. Для каждого из промежутков необходимо решить уравнение и сделать вывод относительно получившихся корней. Корни, удовлетворяющие промежуткам, и дадут окончательный ответ. Пример 3. Решим уравнение |х+3|+|х-1|=6. Найдем корни (нули) каждого выражения, содержащегося под знаком модуля: х+3=0, х= -3; х-1=0, х=1. Эти значения х разбивают числовую прямую на три промежутка: - - -3 + - 1 ++ Решим уравнение отдельно в каждом из получившихся промежутков. В первом промежутке (х < -3) оба выражения, стоящие под знаком модуля отрицательны, поэтому при записи уравнения без абсолютной величины знаки этих выражений меняем на противоположные. Получим уравнение: -х-3-х+1=6. Откуда х= -4. Число -4 является решением данного уравнения, так как оно принадлежит рассматриваемому промежутку. Во втором промежутке (-3 ≤ х < 1) первое выражение положительно, а второе отрицательно. Рассуждая аналогично, получим уравнение: х+1-х+1=6, откуда получаем неверное числовое равенство, то есть в рассматриваемом промежутке уравнение корней не имеет. В последнем промежутке (х ≥ 1) оба выражения положительны, поэтому уравнение записывается так: х+3+х-1=6. Откуда х=2. Это значение удовлетворяет неравенству х ≥ 1. Ответ: -4; 2. Пример 4. Решим уравнение |2-х|=2х+1. Прежде всего, следует установить область допустимых значений. Возникает естественный вопрос, почему в предыдущих примерах не было необходимости этого делать. В этом уравнении в правой части стоит выражение с переменной, которое может быть отрицательным. Таким образом, область допустимых значений – это промежуток [-½; +∞). Найдем нуль выражения, стоящего под знаком модуля: 2-х=0, х=2. + 2 - В первом промежутке: 2-х=2х+1, х=⅓. Это значение принадлежит ОДЗ, значит, является корнем уравнения. Во втором промежутке: -2+х=2х+1, х= -3. -3 не принадлежит ОДЗ, а следовательно не является корнем уравнения. Ответ: ⅓. 3 способ. Графический метод. Знакомство с графиком линейной функции дает мне возможность ввести построение графиков линейных функций, содержащих модули, и изучить влияние модуля на поведение графиков функции. Я начинаю с графика функции y 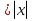 . . Т.к. 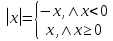 то графиком данной функции являются биссектрисы первой и второй координатных четвертей. то графиком данной функции являются биссектрисы первой и второй координатных четвертей.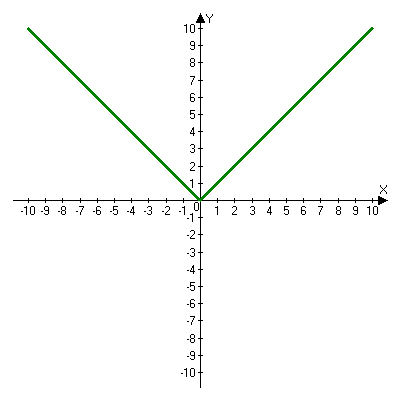 Построим графики функций: а) у=4x-2; б) у= 4 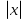 -2; -2;в) у= 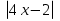 и выведем алгоритм построения графиков функций у = f и выведем алгоритм построения графиков функций у = f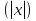 и у = и у =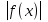 . .Дети знают, какая функция является линейной, умеют строить ее график по двум точкам, находить пересечение графика функции с осями координат. а) у = 4х-2 - линейная функция. График – прямая. Для ее построения отметим точки пересечения графика функции с осями координат: (0;-2) и (0,5;0) 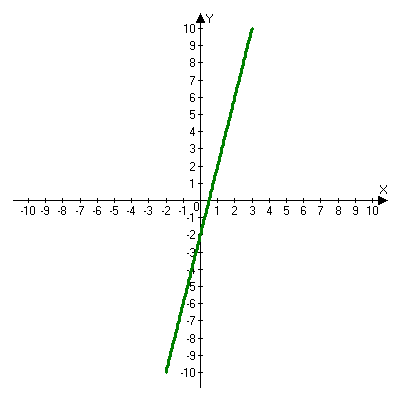 б) у=4 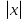 -2. -2.Вспоминаем определение модуля: . 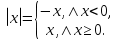 Смена знака выражения, стоящего под модулем, происходит при х = 0, т.е. у (х) = 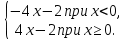 На каждом из интервалов построим графики соответствующих функций и получим 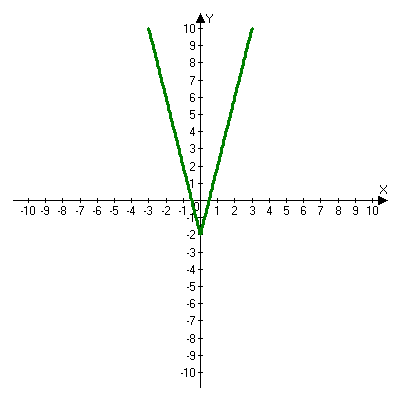 Анализируя полученный график, можно заметить, что он может быть получен путем симметричного отображения относительно оси Оy графика функции у = 2х-1, расположенного справа от оси Оу. 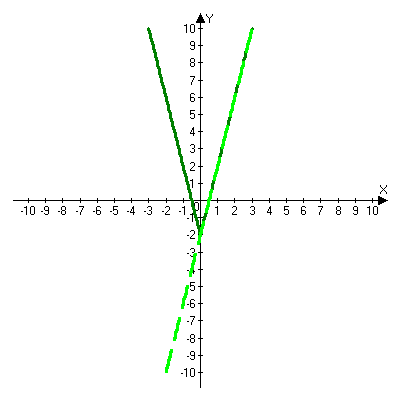 После построения нескольких графиков такого типа можно сделать вывод: для построения графика функции у=f 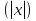 достаточно построить график функции у=f достаточно построить график функции у=f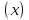 при при 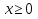 и отобразить его симметрично относительно оси ординат. и отобразить его симметрично относительно оси ординат.в) у= 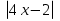 Раскроем модуль. Для этого приравняем к 0 выражение, стоящее под знаком модуля, и узнаем, при каком значении х оно меняет знак: 4х - 2 = 0, х = 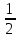 . .При х 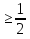 , у = 4х - 2, при х , у = 4х - 2, при х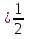 , у = - 4х+2. , у = - 4х+2.Это значит, что при х 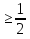 мы будем строить график функции у=4х - 2, а при х мы будем строить график функции у=4х - 2, а при х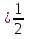 - график функции у = - 4х+2. - график функции у = - 4х+2.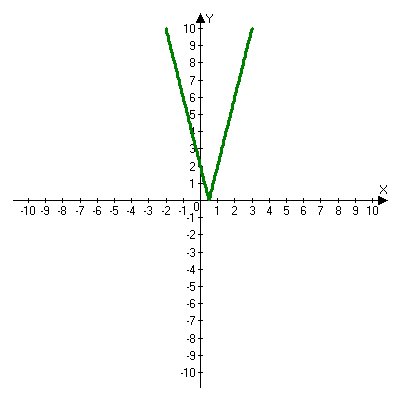 Анализируя полученный график, можно заметить, что он может быть получен путем симметричного отражения относительно оси абсцисс графика функции у = 4х - 2, расположенного ниже оси Ох. После построения нескольких графиков такого типа можно сделать вывод: для построения графика функции у= 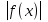 достаточно построить график функции у=f достаточно построить график функции у=f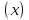 и его часть, расположенную в нижней полуплоскости, отобразить симметрично относительно оси Ох. и его часть, расположенную в нижней полуплоскости, отобразить симметрично относительно оси Ох. 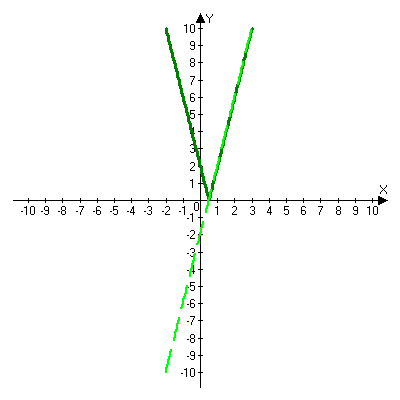 После того как учащиеся освоят построения графиков такого вида, можно перейти к построению более сложных примеров: График функции у= 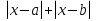 , b > a, имеет вид «корыта», поставленного на квадрат со стороной b-a. Технология построения таких графиков схожа с решением уравнения методом интервалов: , b > a, имеет вид «корыта», поставленного на квадрат со стороной b-a. Технология построения таких графиков схожа с решением уравнения методом интервалов:- необходимо найти корни (нули) каждого выражения, содержащегося под знаком модуля. Эти значения х разбивают числовую прямую на промежутки. На каждом из данных промежутков определяем знаки подмодульных выражений, раскрываем модули и определяем функцию. Таким образом для каждого промежутка строится свой график. Например: у=|х+3|+|х-1| Найдем корни (нули) каждого выражения, содержащегося под знаком модуля: х+3=0, х= -3; х-1=0, х=1. Эти значения х разбивают числовую прямую на три промежутка: - - -3 + - 1 ++ При х< -3 у=-х-3-х+1, у= -2х -2 При -3≤ х ≤ 1 у=х+3-х+1, у= 4 При х> 1 у= х+3+х-1, у= 2х +2. Получаем график: 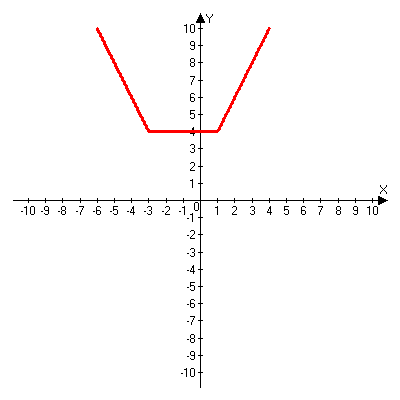 Аналогично строим график функции вида у= 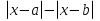 , который похож на «ступеньки»: , который похож на «ступеньки»:Например, у=|х+3|-|х-1| 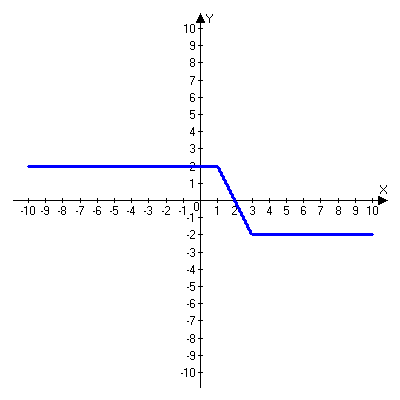 Или график функции у= 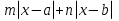 , m, n > 0 имеет вид «косого корыта» - перекос происходит из-за различия коэффициентов m и n. , m, n > 0 имеет вид «косого корыта» - перекос происходит из-за различия коэффициентов m и n.у=3|х-3|+2|х-1| 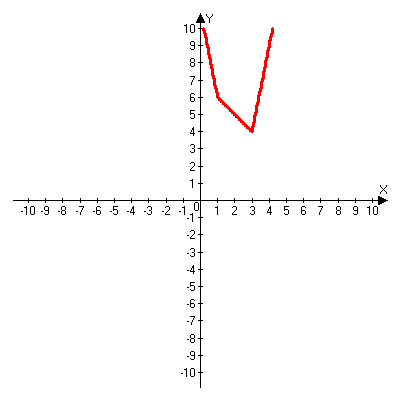 Если учащиеся освоили построение графиков функций с модулем, то можно переходить к графическому способу решения уравнений. Суть данного метода заключается в использовании графиков функций для нахождения корней уравнения. Этот метод реже других применяют для решения уравнений, содержащих модуль, так как, во-первых, он занимает достаточно много времени и не всегда рационален, а, во-вторых, результаты, полученные при построении графиков, не всегда являются точными. Пример 5. Решим уравнение |х+1|=2. Построим графики функций у=|х+1| и у=2. 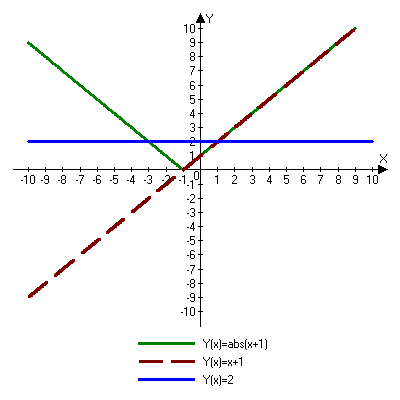 Для построения графика у=|х+1|, построим график функции у=х+1, а затем отразим часть прямой, лежащую ниже оси ОХ. Абсциссы точек пересечения графиков и есть корни уравнения: х1=1, х2= -3. Ответ: 1; -3. Рассмотрим еще один пример: |х-7|-|х-8|=1. Решим это уравнение двумя способами. а) метод интервалов: Найдем концы интервалов: х=7 и х=8. Отметим эти числа на координатной прямой, а затем решим уравнение в каждом из получившихся промежутков: -х+7+х-8=1, х-7+х-8=1, х-7-х+8=1, -1≠1, 2х=16, 1=1, 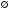 х=8 х – любое число х=8 х – любое число Ответ: [8;+∞). б) графический метод: для решения уравнения построим в одной системе координат графики функций у = |х-7|-|х-8| и у=1 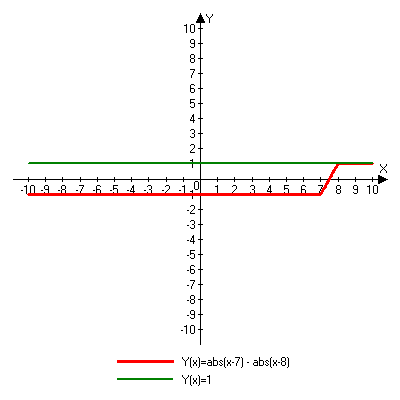 Завершая рассмотрение различных способов решения уравнений, содержащих знак модуля, еще раз отметим тот важный факт, что ни один из них не является универсальным и для получения наилучших результатов необходимо добиваться того, чтобы ученик овладел возможно большим количеством методов решения, оставляя право выбора решения за собой. Над проблемой применения различных способов для решения уравнений с модулем я работаю четвертый год. За это время мною разработана и внедрена в практику методика обучения учащихся решению уравнений с модулем, которую я применяю на факультативных занятиях. Цель внедрения данной методики заключается в стремлении повысить качество умения решать уравнения, содержащие абсолютную величину. За это время я убедилась, что решение уравнений, содержащих знак абсолютной величины, составляет большую трудность для учащихся. В начале обучения использованию различных методов для решения уравнений ученики относились к ним настороженно, стараясь, как можно чаще использовать один метод для решения всех уравнений, что иногда приводило к затруднениям. Однако, со временем, поняв, что к каждому уравнению можно подобрать наиболее эффективный метод решения, дети стали использовать для решения все способы в зависимости от уравнения. Таким образом, можно сделать следующий вывод: систематическое использование различных способов для решения уравнений, содержащих абсолютную величину, приводит не только к повышению интереса к математике, повышению творческой активности школьников, но и повышает уверенность детей в собственных силах, так как у них имеется возможность выбора того способа решения, который наиболее эффективен в каждом конкретном случае. Приложение Зачетная работа по теме: «Решение уравнений с модулем» Решите уравнение с модулем: Вариант 1 1) 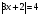 2) 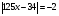 3) 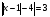 4) 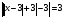 5) 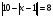 6) 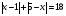 7) 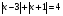 8) 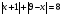 9) 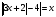 10) 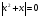 Вариант 2 1) 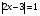 2) 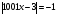 3) 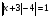 4) 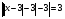 5) 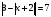 6) 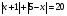 7) 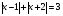 8) 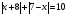 9) 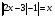 10) 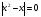 |