Gérard Desargues ) (1591-1661) известный французский геометр
 Скачать 37.25 Kb.
|
 Жерар Дезарг (фр. Gérard Desargues) (1591—1661) — известный французский геометр. Принадлежал к аристократической фамилии и начал службу в рядах армии. При осаде Ла-Рошели познакомился и подружился с Декартом. Оставив службу, поселился в Париже, где вошел в кружок Шатеро-Лефевра, у которого встречал Гассенди, Буйо, Роберваля, Паскаля и других математиков того времени. Основатель проективной геометрии. После него остались следующие сочинения:
Теорема Дезарга: Если прямые проходящие через соответствующие вершины двух трехвершинников пересекаются в одной точке, то точки пересечения соответствующих сторон этих трехвершинников лежат на одной прямой. ABA'B'=P, ACA'C'=Q, BCB'C'=R, AA'BB'CC'=O, Доказать: P, Q, R лежат в одной прямой Доказательство: Р 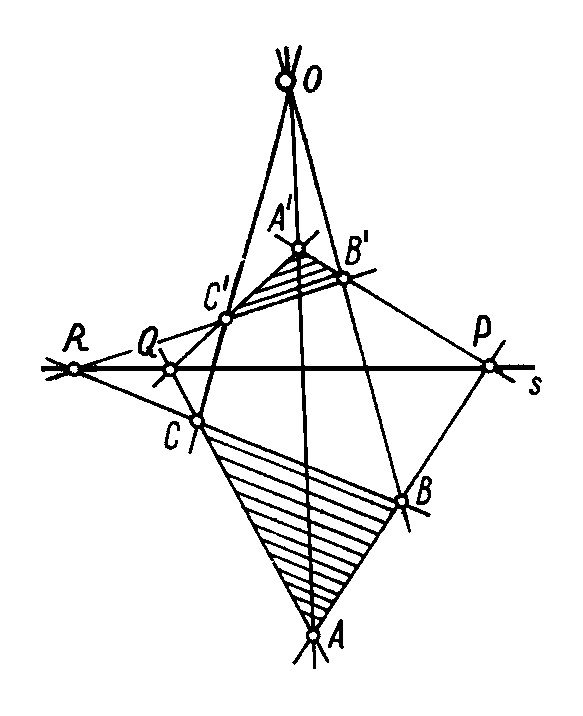 ассмотрим векторы  порождающие соответствующие точки, так как А,А',О лежат на одной прямой, то векторы порождающие их линейно зависимы, т.е.  =  . Из того, что В', В, О - лежат на одной прямой  , , - линейно зависимы =  Точки С, С', О - лежат на одной прямой = γ +   = = γ +   ,, - линейно зависимы точки А, В, Р одной прямой,  ,, - линейно зависимы точки А', В', Р' одной прямой.P=ABA'B'  -  = -  = (2), , - линейно зависимы точки А, С, Q одной прямой. - линейно зависимы точки А', С', Q' одной прямой.Следовательно, Q=АСА'С'  - = -  =  (3),, –линейно зависимы точки В, С, R одной прямой.,', ' –линейно зависимы точки В', С', R' одной прямойСледовательно, R=ВСВ'С'. Составим выражение:  =--++-=  - векторы , , линейно зависимы точки P, Q, R лежат на одной прямой.Теорема доказана. История Теорема Дезарга была открыта французским геометром Дезаргом: она, вместе с двумя другими, из которых одна есть её обратная, была помещена в конце сочинения Traité de perspective, составленного Боссом согласно началам и методу Дезарга и появившегося в 1636 году. В этом сочинении было отмечено, что это утверждение очевидно, когда треугольники находятся в двух разных плоскостях; рассмотрение же случая, когда они лежат в одной плоскости, доставляет один из первых примеров употребления теореме Менелая у новых геометров. Известность теорема Дезарга получила в начале XIX века благодаря её употреблению в работах Брианшона и Понселе. О доказательстве Одно из самых распространённых доказательств основывается на переходе в трёхмерное пространство — достаточно представить оба треугольника двумя сечениями трёхгранной пирамиды. Вся картина при этом рассматривается как проекция на плоскость пространственной структуры. Возможно также доказательство через теорему Менелая. Конфигурация Дезарга Точки и прямые в теореме Дезарга образуют так называемую конфигурацию Дезарга. Здесь через каждую из 10 точек проходят 3 прямые и на каждой из 10 прямых лежат 3 точки. При этом любая из 10 точек может быть принята за «вершину трёхгранной пирамиды» («дезаргову точку») в приведённом выше доказательстве. Любая прямая, может быть взята как «дезаргова прямая». Фиксирование дезарговой точки или дезарговой прямой полностью определяет всю конфигурацию. Теорема Дезарга и аксиоматика проективной геометрии При построении проективной геометрии плоскости, без выхода в трёхмерное пространство, теорема Дезарга не выводится из основных аксиом проективной плоскости. Это означает, что возможно построить проективную плоскость, где теорема Дезарга не верна (см. недезаргова геометрия). При построении дезарговой проективной плоскости утверждение теоремы Дезарга добавляют к системе аксиом проективной плоскости в качестве ещё одной аксиомы. Вариации и обобщения Понселе основал на ней свою изящную теорию гомологических фигур. Он называл два треугольника, о которых идет речь в теореме Дезарга, гомологическими, точку пересечения прямых, соединяющих попарно их вершины, центром гомологии, и прямую, на которой попарно пересекаются их стороны, — осью гомологии. |