№
|
Задание
|
Ответ
|
1
|
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
|
|
2
|
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен  , а высота равна 2.
|
|
3
|
Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна 2.
|
|
4
|
Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
|
|
5
|
Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
|
|
6
|
Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
|
|
7
|
Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
|
|
8
|
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
|
|
9
|
Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны .
|
|
10
|
Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.
|
|
11
|
Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна .
|
|
12
|
Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен .
|
|
13
|
Диагональ куба равна  . Найдите его объем.
|
|
14
|
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
|
|
15
|
Одна из граней прямоугольного параллелепипеда — квадрат. Диагональ параллелепипеда равна  и образует с плоскостью этой грани угол 45 . Найдите объем параллелепипеда
|
|
16
|
Гранью параллелепипеда является ромб со стороной 1 и острым углом 600. Одно из ребер параллелепипеда составляет с плоскостью этой грани угол 600 и равно 2. Найдите объем параллелепипеда.
|
|
17
|
Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны  и наклонены к плоскости основания под углом 300.
|
|
18
|
В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
|
|
19
|
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60. Высота пирамиды равна 6. Найдите объем пирамиды.
|
|
20
|
Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
|
|
21
|
Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1 : 2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.
|
|
22
|
Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.
|
|
23
|
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.
|
|
24
|
Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.
|
|
25
|
Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
|
|
26
|
Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен , а высота равна 2.
|
|
27
|
Найдите площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой равна 6 и высота равна 4.
|
|
28
|
Найдите объем пирамиды, высота которой равна 6, а основание — прямоугольник со сторонами 3 и 4.
|
|
29
|
В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро пирамиды.
|
|
30
|
Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.
|
|
31
|
Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.
|
|
32
|
Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 450. Найдите объем пирамиды.
|
|
33
|
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.
|
|
34
|
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.
|
|
35
|
Куб вписан в шар радиуса . Найдите объем куба.
|
|
36
|
Найдите угол ABD1 прямоугольного параллелепипеда, для которого  ,  ,  . Ответ дайте в градусах.
|
|
37
|
Найдите угол  прямоугольного параллелепипеда, для которого  ,  ,  . Ответ дайте в градусах.
|
|
38
|
В правильной шестиугольной призме  все ребра равны 1. Найдите расстояние между точками  и  .
|
|
39
|
В правильной шестиугольной призме все ребра равны  . Найдите расстояние между точками  и .
|
|
40
|
В правильной шестиугольной призме все ребра равны 1. Найдите тангенс угла  .
|
|
41
|
В правильной шестиугольной призме все ребра равны 1. Найдите угол  . Ответ дайте в градусах.
|
|
42
|
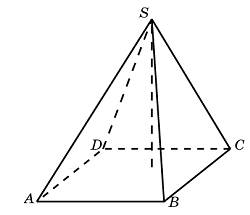
В правильной четырехугольной пирамиде  точка  — центр основания,  вершина,  ,  . Найдите боковое ребро  .
|
|
43
|
В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина,  , . Найдите длину отрезка  .
|
|
44
|
В правильной четырехугольной пирамиде SABCD точка O — центр основания, S — вершина, , . Найдите длину отрезка  .
|
|
45
|
В прямоугольном параллелепипеде  известно, что  ,  ,  . Найдите длину ребра  .
|
|
46
|
В прямоугольном параллелепипеде ребро  , ребро  , ребро  . Точка K — середина ребра  . Найдите площадь сечения, проходящего через точки  ,  и  .
|
|
47
|
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер:  ,  ,  . Найдите площадь сечения, проходящего через вершины , A1 и  .
|
|
48
|
В правильной четырёхугольной пирамиде SABCD с основанием  боковое ребро  равно 5, сторона основания равна  . Найдите объём пирамиды.
|
|
Скачать 83.81 Kb.