№
|
Задание
|
ответ
|
1
|
В ABC C = 900, CH — высота, AB = 13, 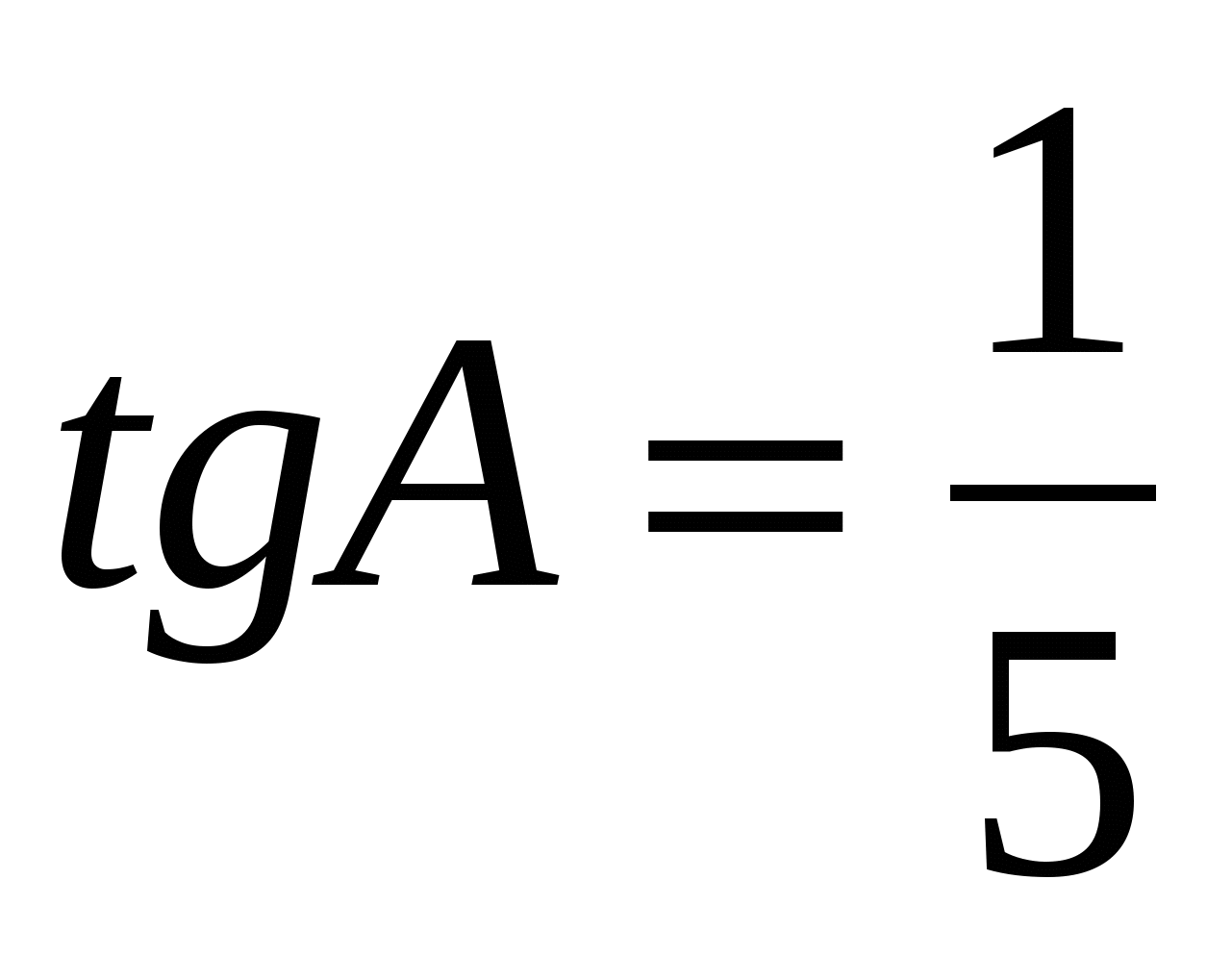 . Найдите AH. . Найдите AH.
|
12,5
|
2
|
В ABC C = 900, CH — высота, AB = 13, 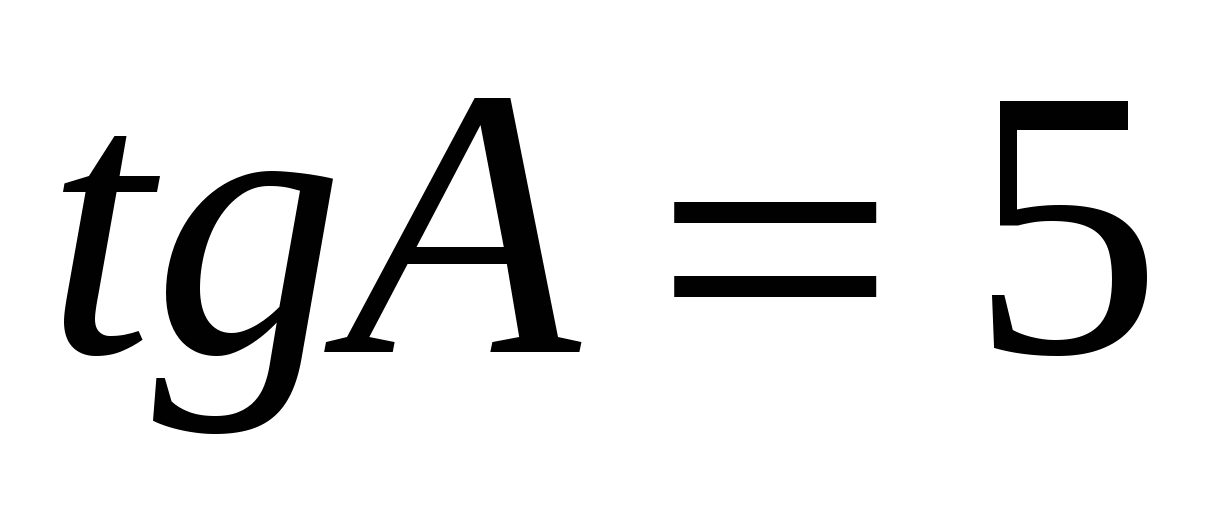 . Найдите BH. . Найдите BH.
|
12,5
|
3
|
В ABC C = 900, AB = 13, 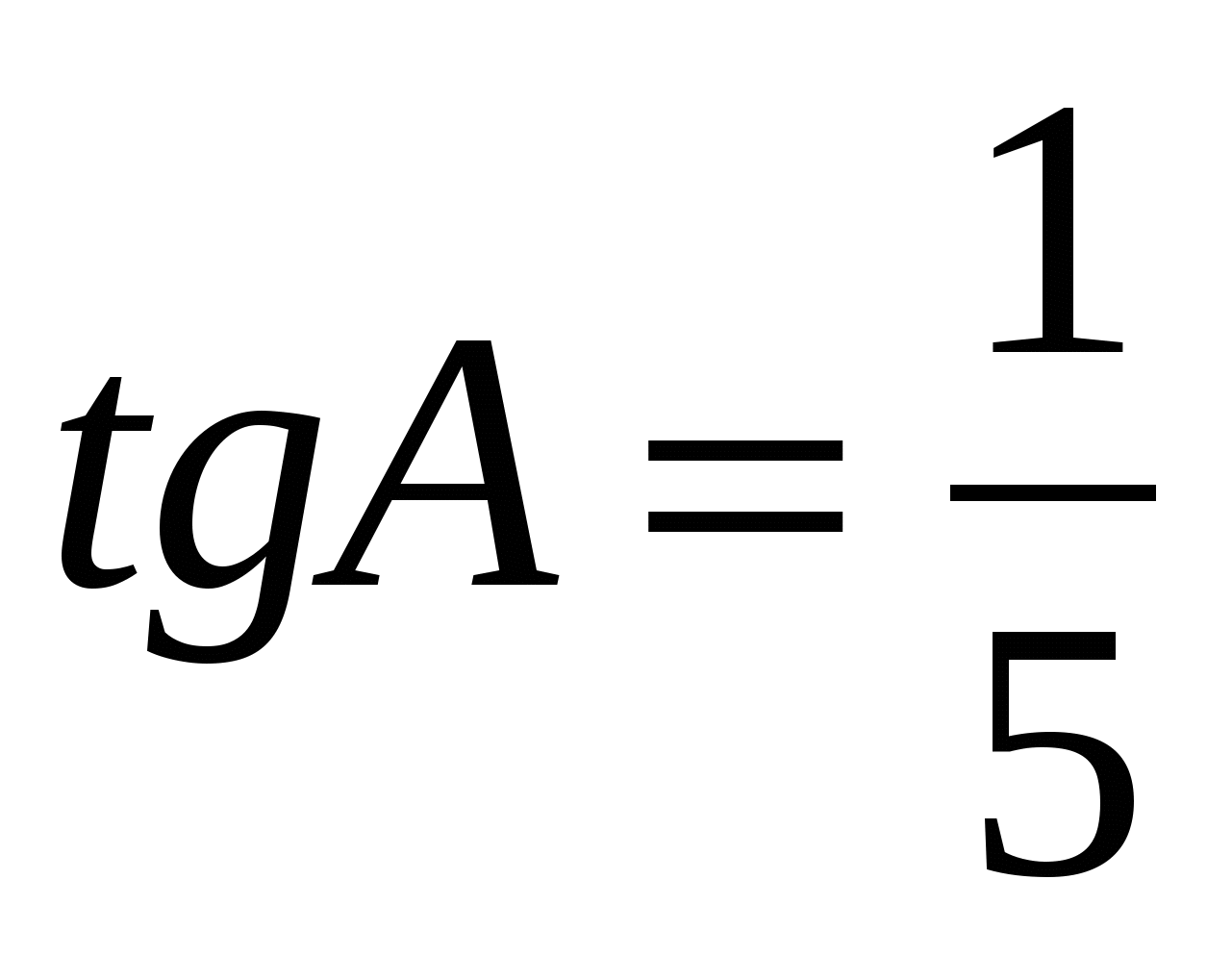 . Найдите высоту CH. . Найдите высоту CH.
|
2,5
|
4
|
В ABC C = 900, CH — высота, BC = 3, 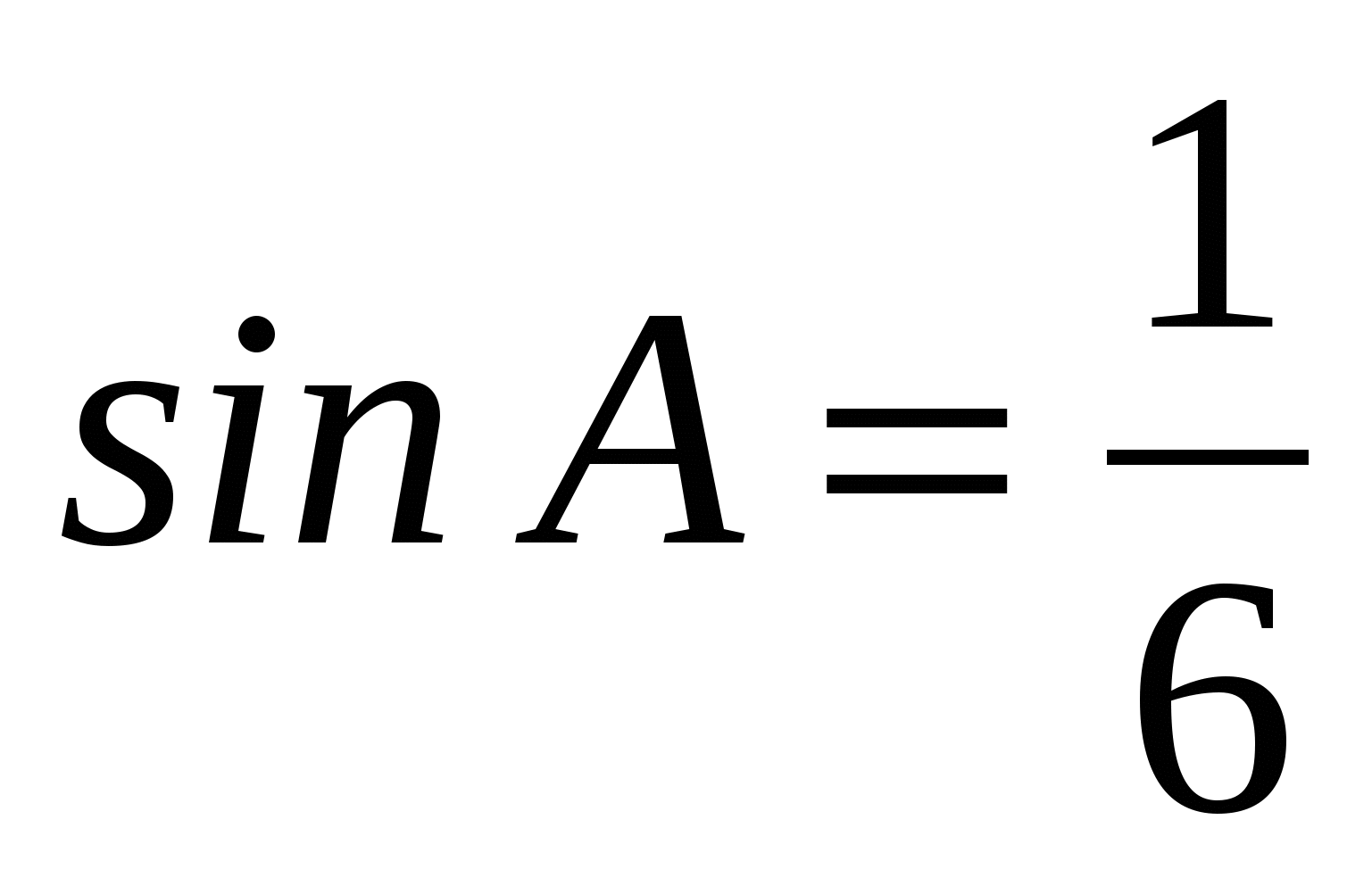 . Найдите AH. . Найдите AH.
|
17,5
|
5
|
В ABC C = 900, CH — высота, BC = 8,  . Найдите BH. . Найдите BH.
|
4
|
6
|
В ABC C = 900, BC = 5, 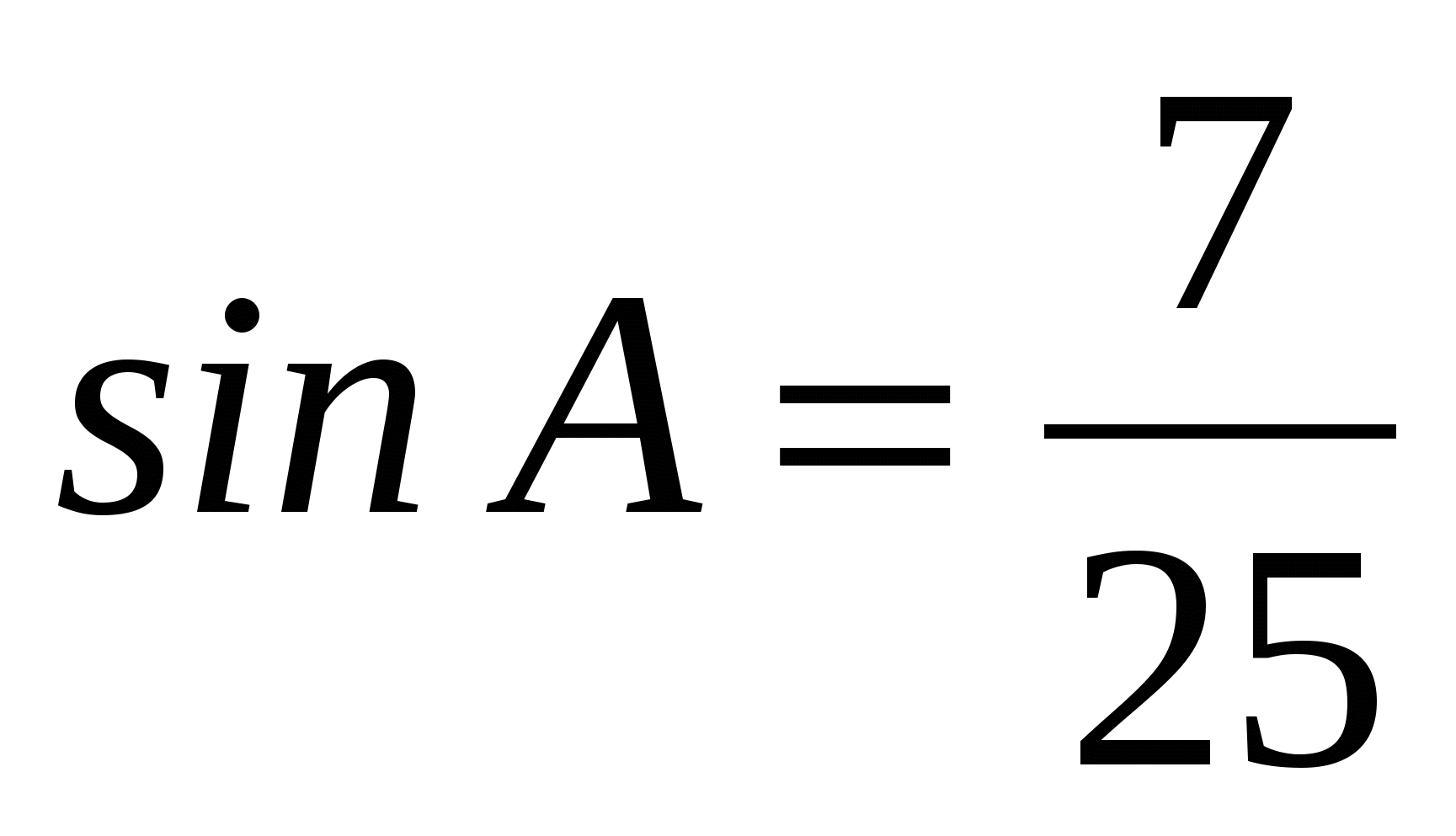 . Найдите высоту CH. . Найдите высоту CH.
|
4,8
|
7
|
В ABC C = 900, CH — высота, BC = 3,  . Найдите AH. . Найдите AH.
|
17,5
|
8
|
В ABC C = 900, CH — высота, BC = 5, 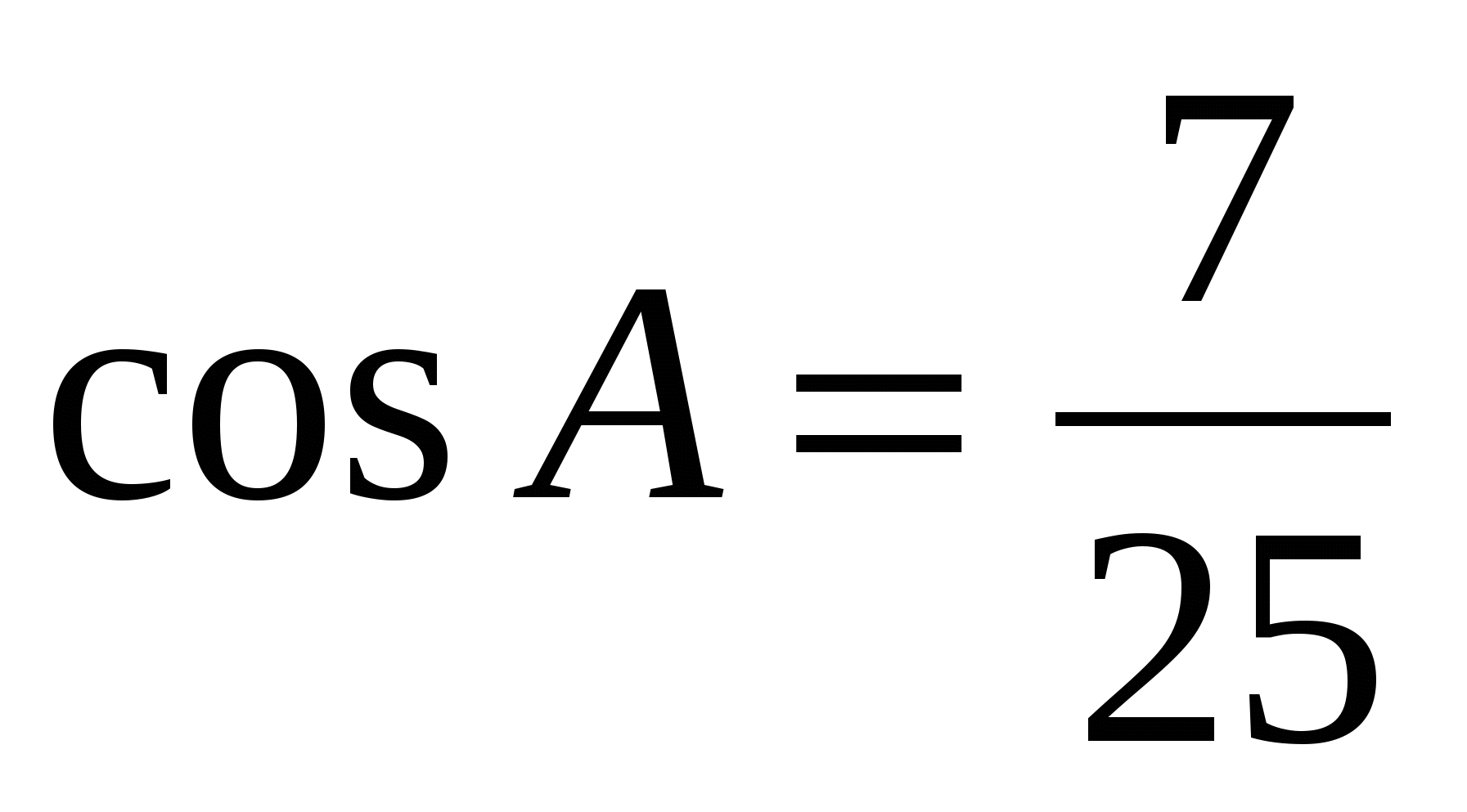 . Найдите BH. . Найдите BH.
|
4,8
|
9
|
В ABC C = 900, BC = 8, 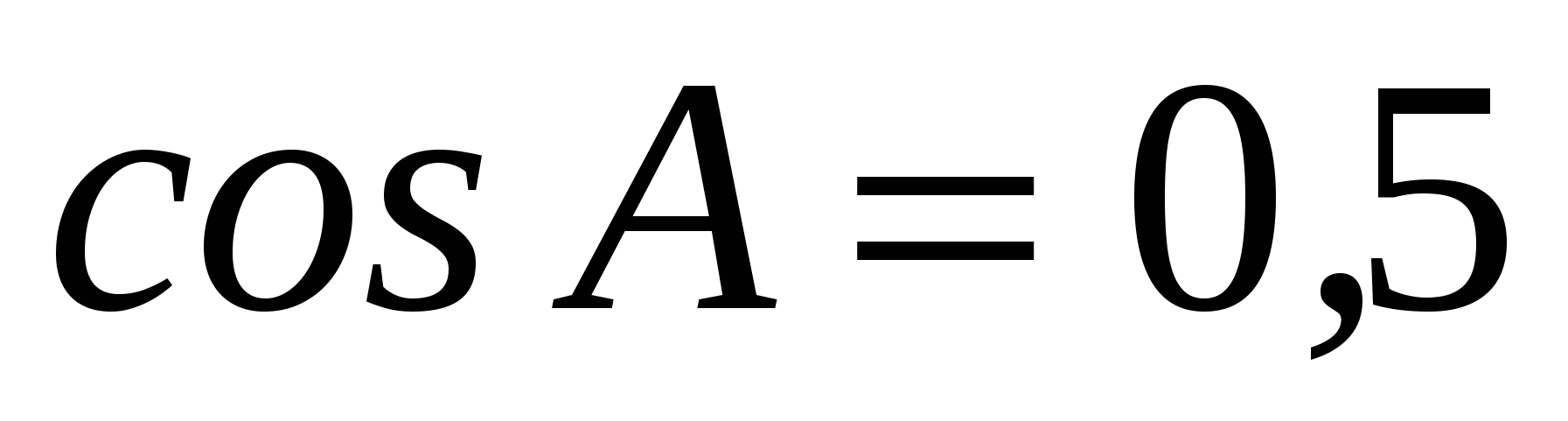 . Найдите высоту CH. . Найдите высоту CH.
|
4
|
10
|
В ABC C = 900, CH — высота, AC = 3,  . Найдите BH. . Найдите BH.
|
17,5
|
11
|
В ABC C = 900, CH — высота, AC = 3,  . Найдите BH. . Найдите BH.
|
17,5
|
12
|
В ABC AC = BC = 5, 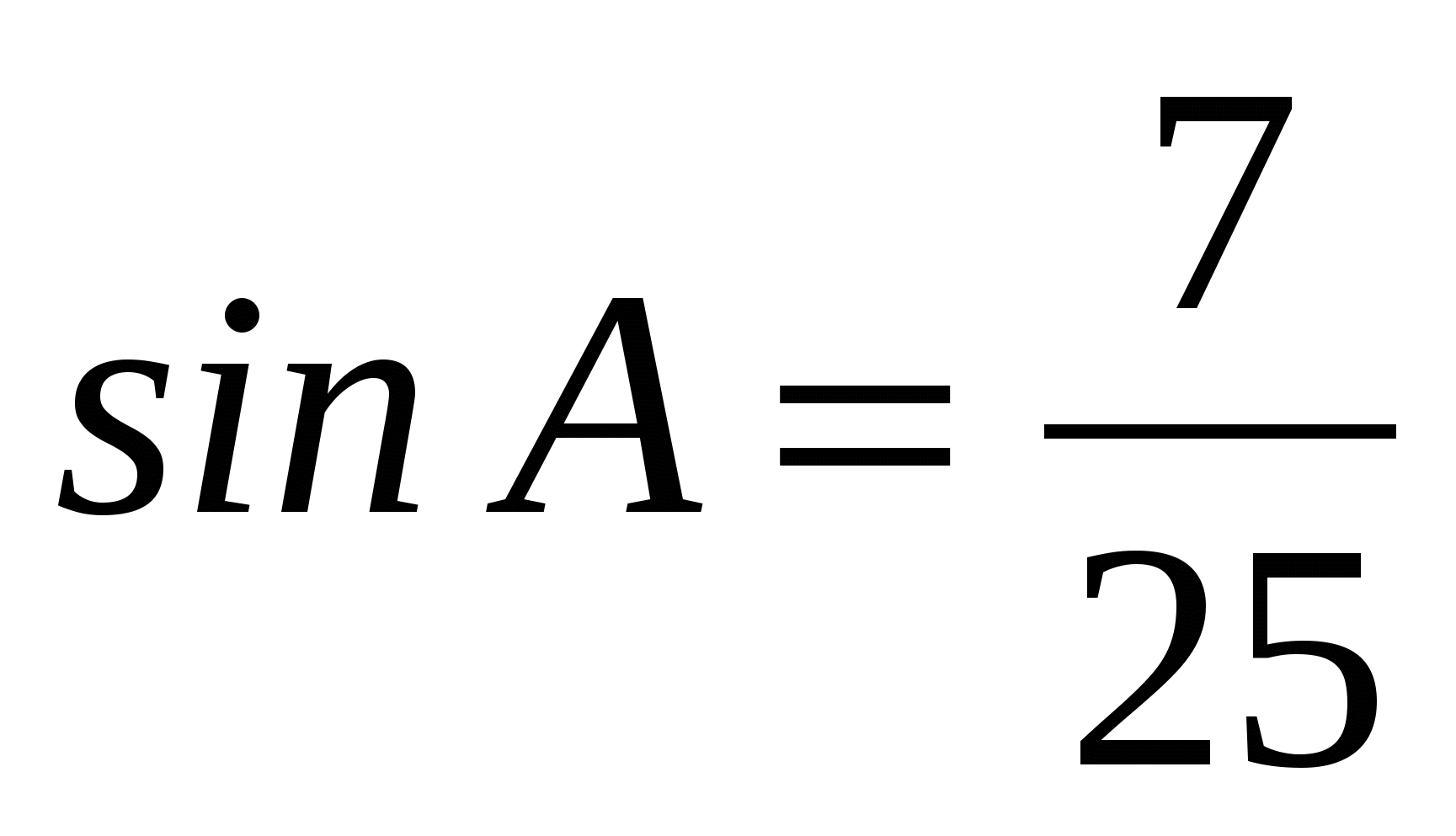 . Найдите AB. . Найдите AB.
|
9,6
|
13
|
В ABC AC = BC, AB = 9,6, 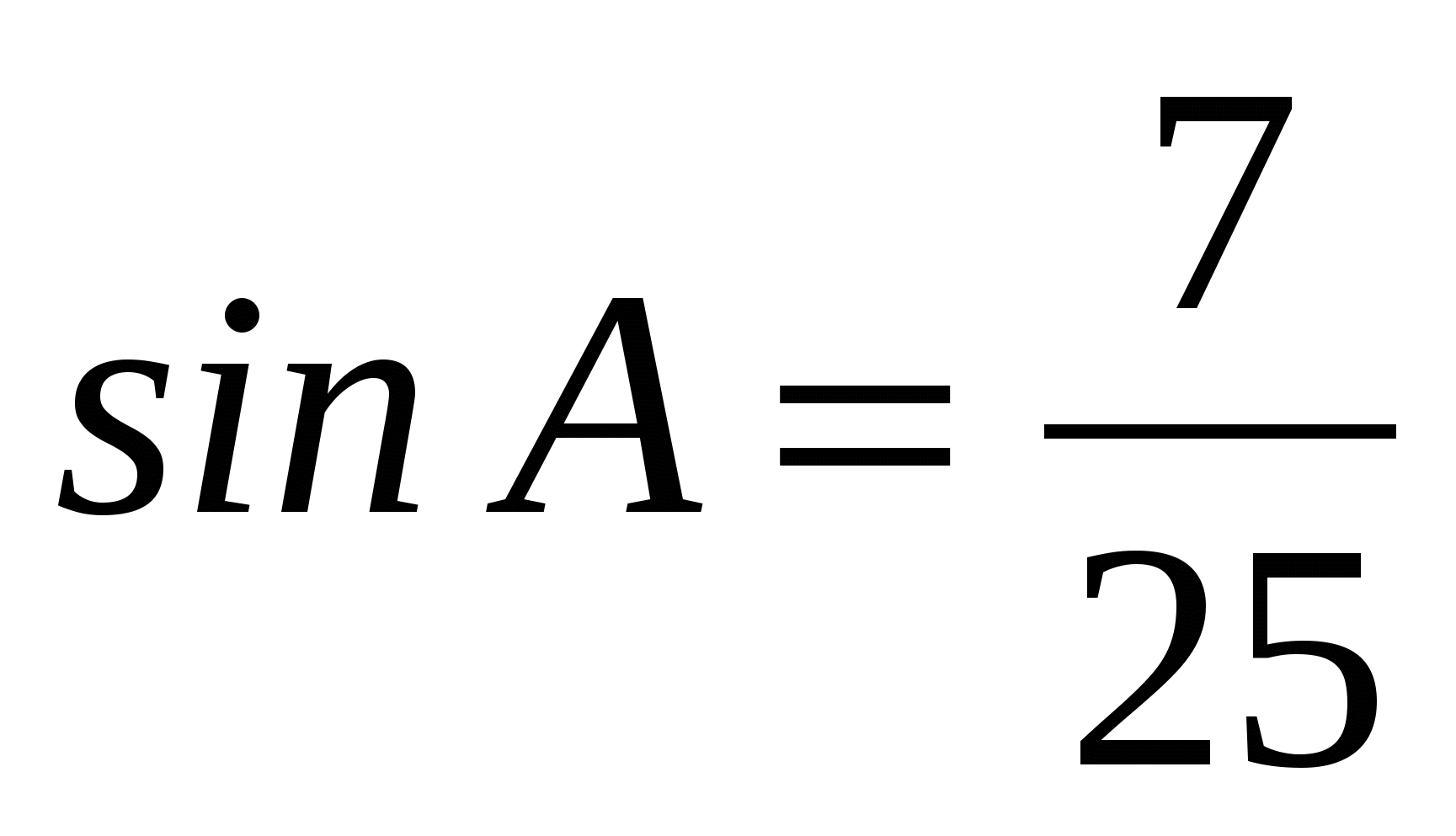 . Найдите AC. . Найдите AC.
|
5
|
14
|
В ABC AC = BC = 8, 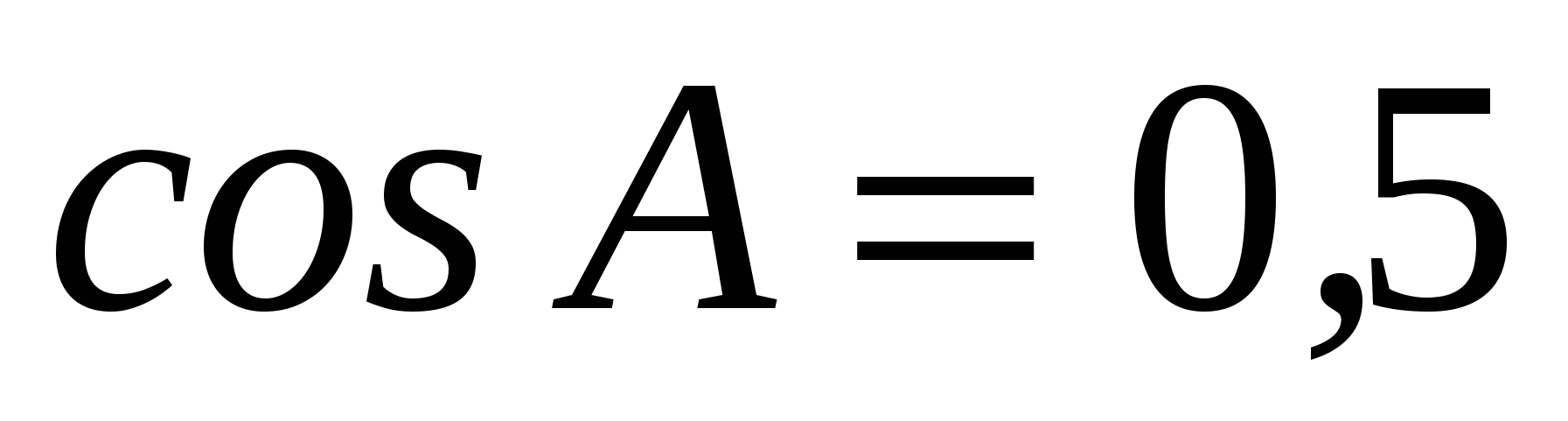 . Найдите AB. . Найдите AB.
|
8
|
15
|
В ABC AC = BC, AB = 8, 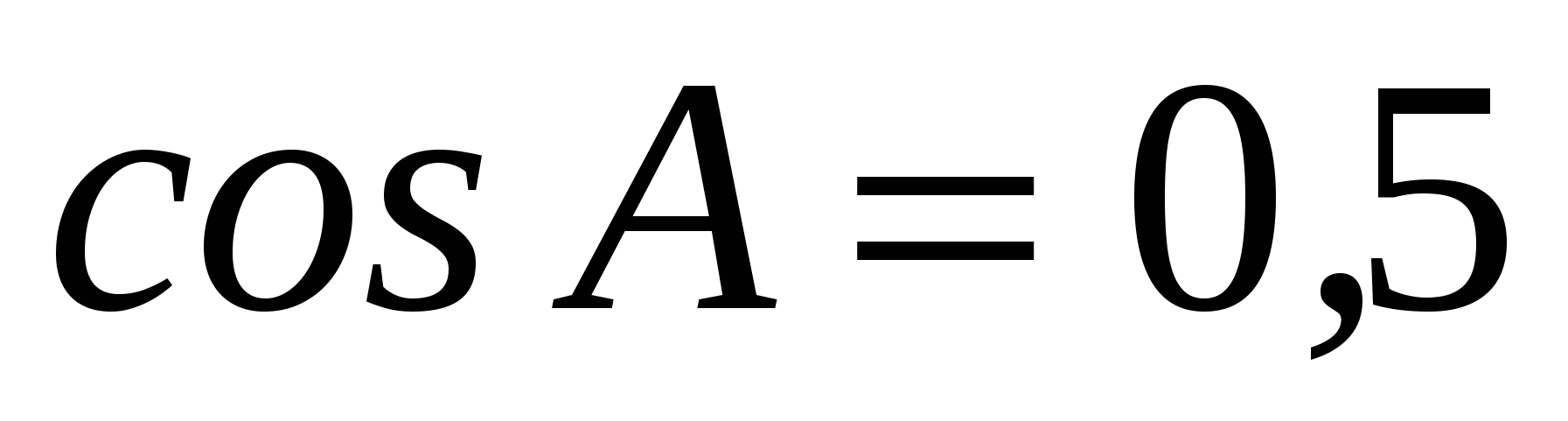 . Найдите AC. . Найдите AC.
|
8
|
16
|
В ABC AC = BC = 7, 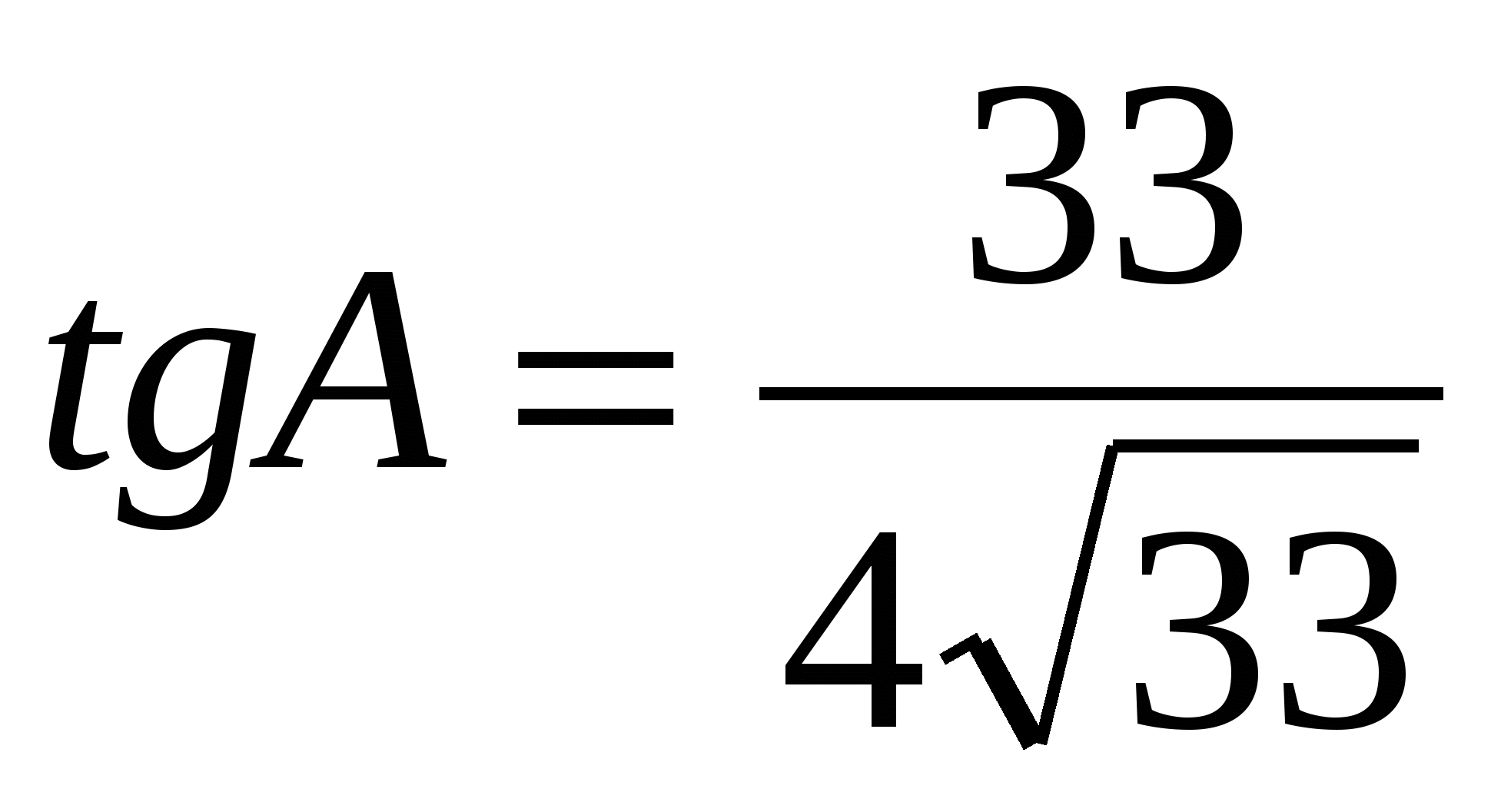 . Найдите AB. . Найдите AB.
|
8
|
17
|
В ABC AC = BC, AB = 8, 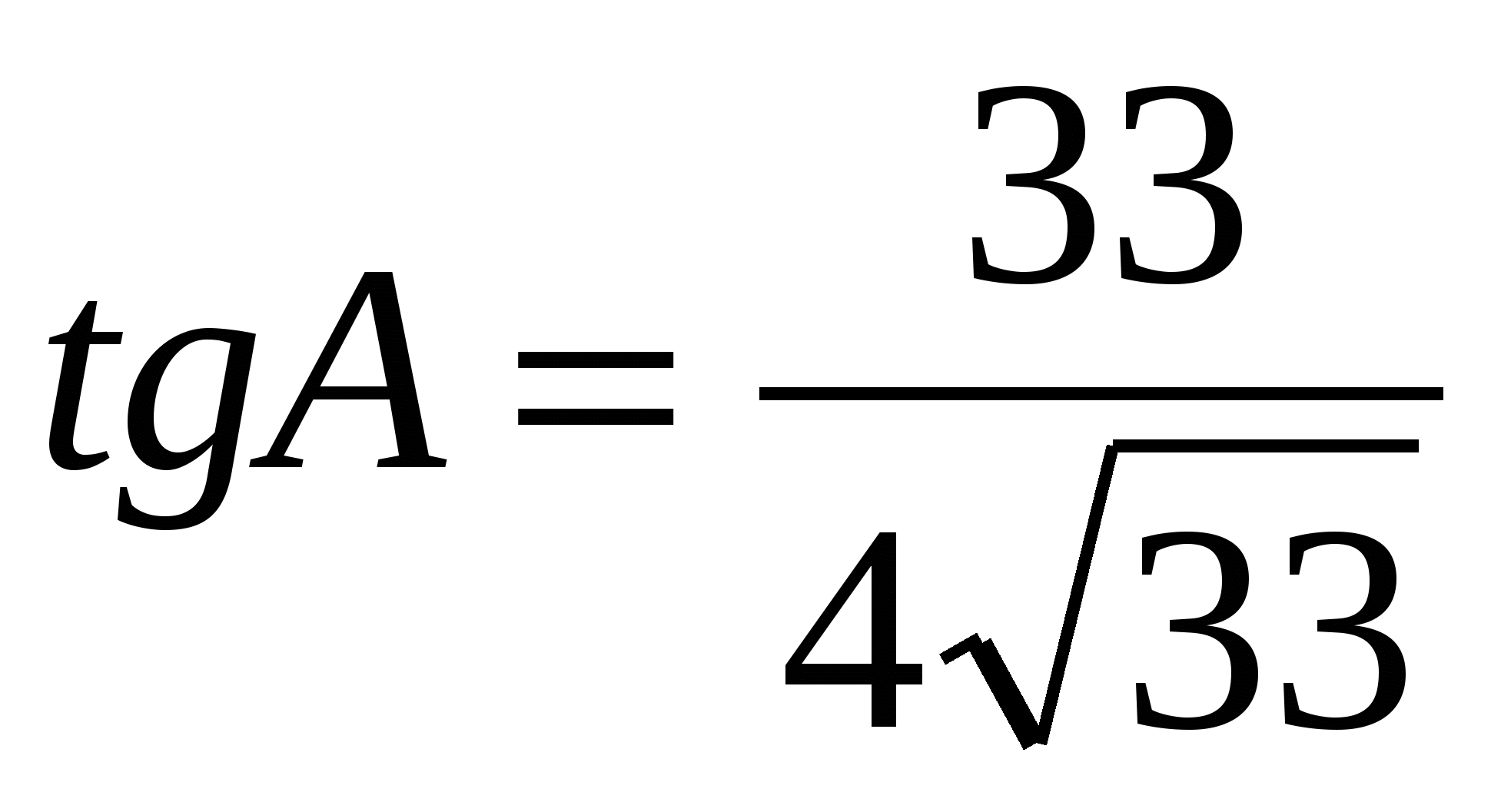 . Найдите AC. . Найдите AC.
|
7
|
18
|
В ABC AC = BC, AB = 8, 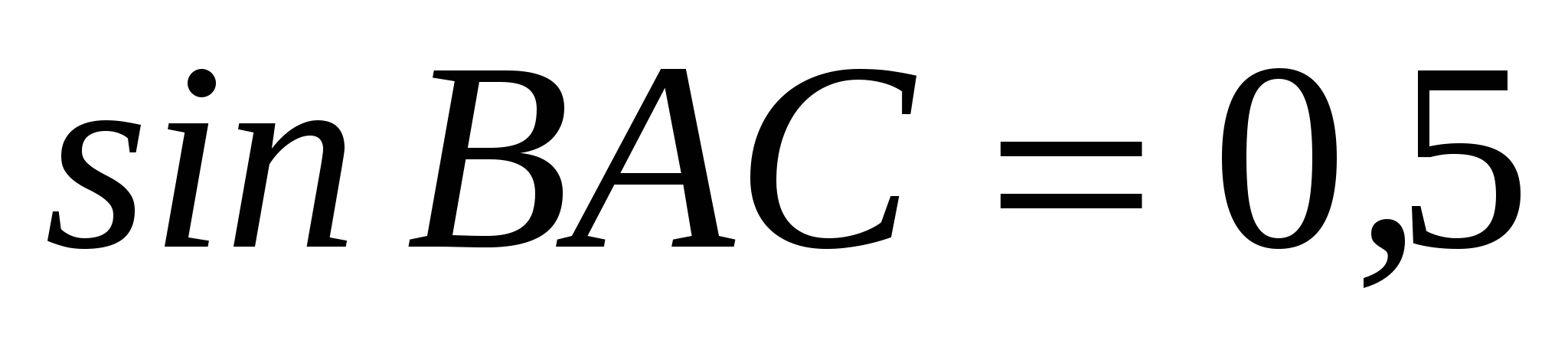 . Найдите высоту AH. . Найдите высоту AH.
|
4
|
19
|
В ABC AC = BC, AH — высота, AB = 5, 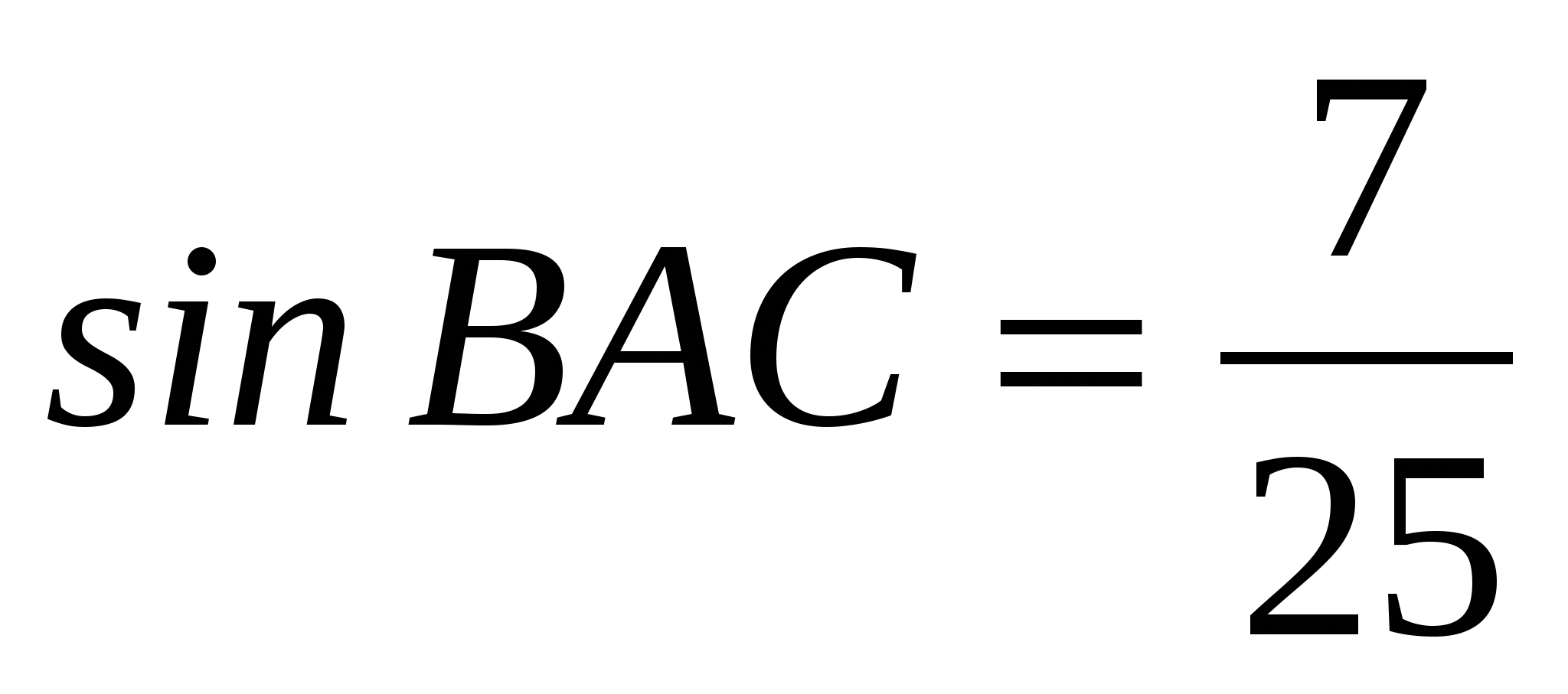 . Найдите BH. . Найдите BH.
|
4,8
|
20
|
В ABC AC = BC, AB = 5, . Найдите высоту AH. . Найдите высоту AH.
|
4,8
|
21
|
В ABC AC = BC, AH — высота, AB = 8, . Найдите BH. . Найдите BH.
|
4
|
22
|
В ABC AC = BC, AB = 7, 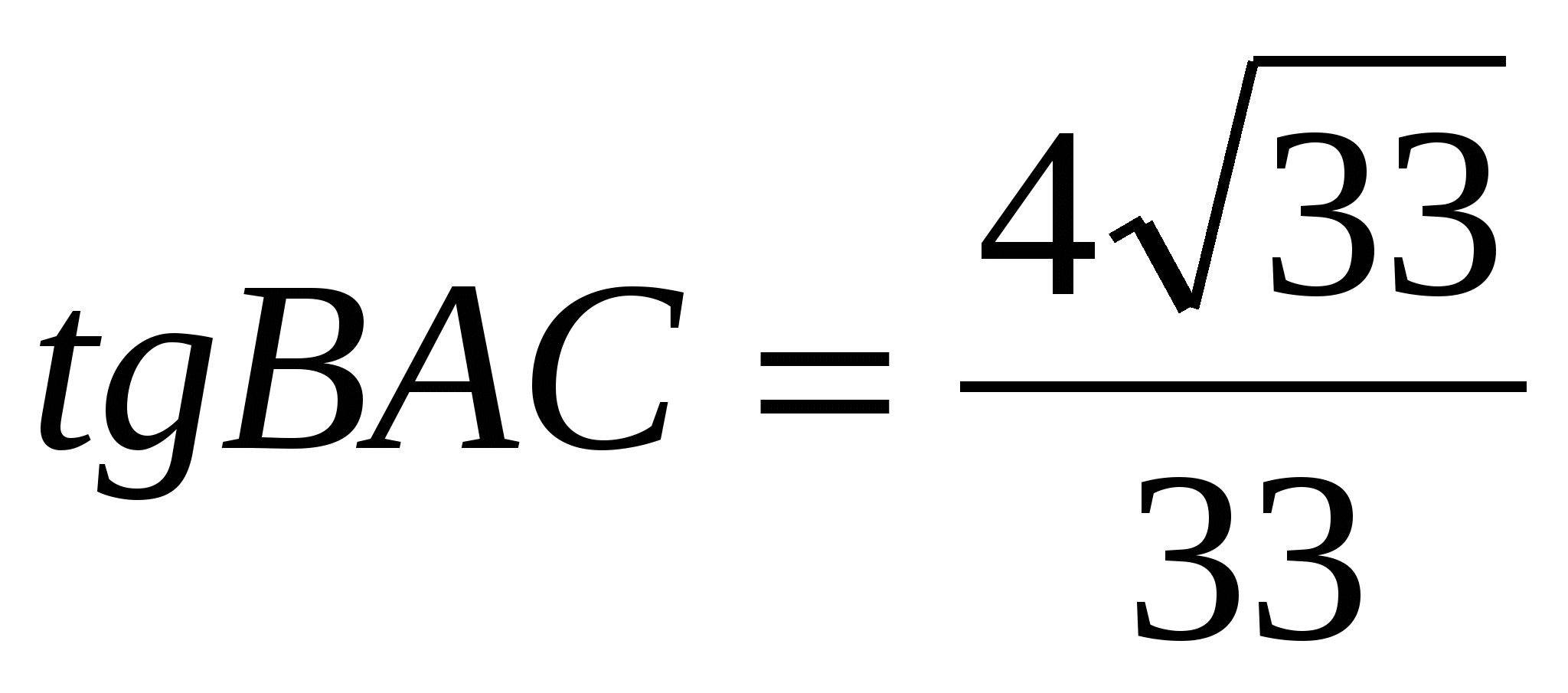 . Найдите высоту AH. . Найдите высоту AH.
|
4
|
23
|
В ABC AC = BC, AH — высота, AВ = 7, 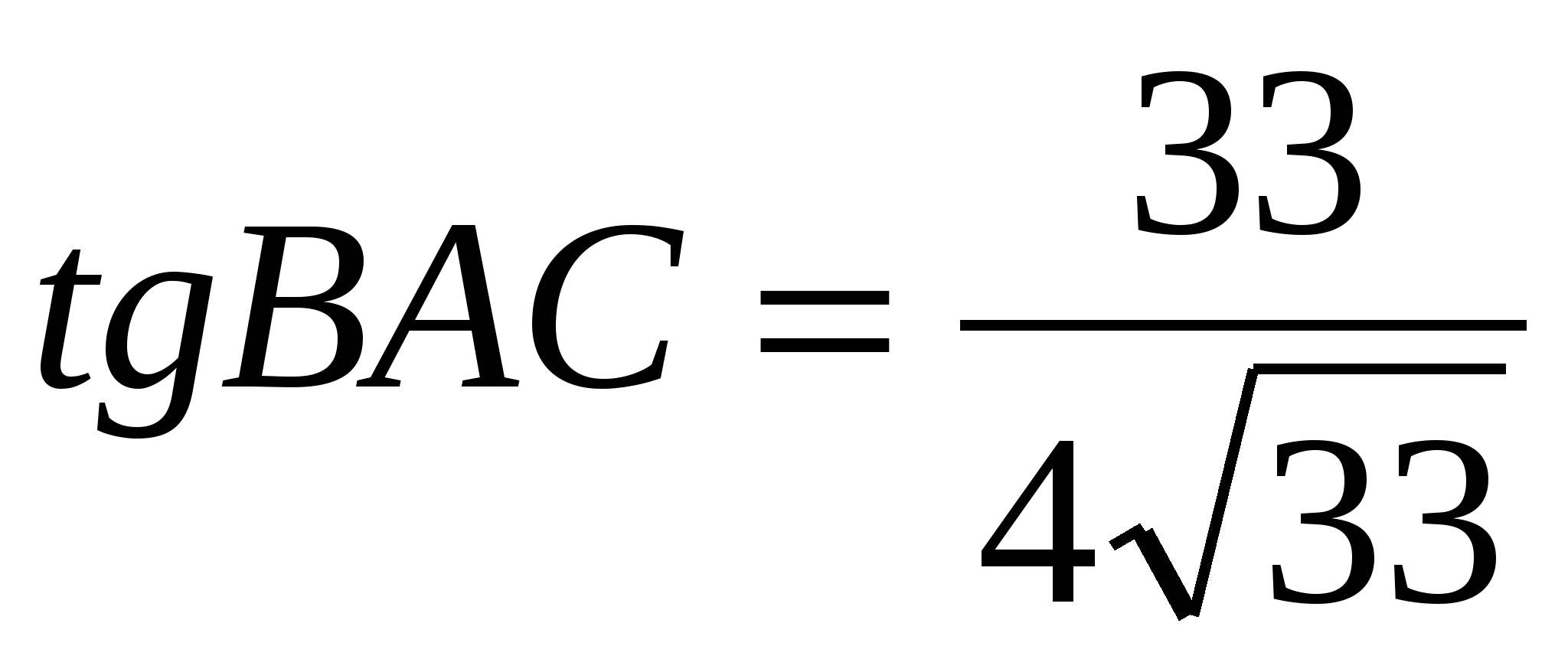 . Найдите BH. . Найдите BH.
|
4
|
24
|
В ABC 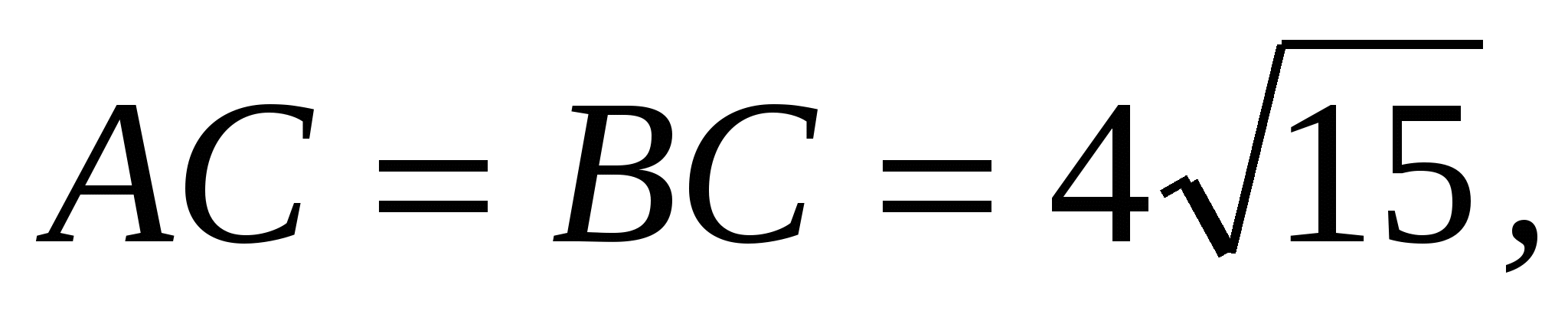  . Найдите высоту AH. . Найдите высоту AH.
|
7,5
|
25
|
В ABC АС = ВС =27, AH — высота, 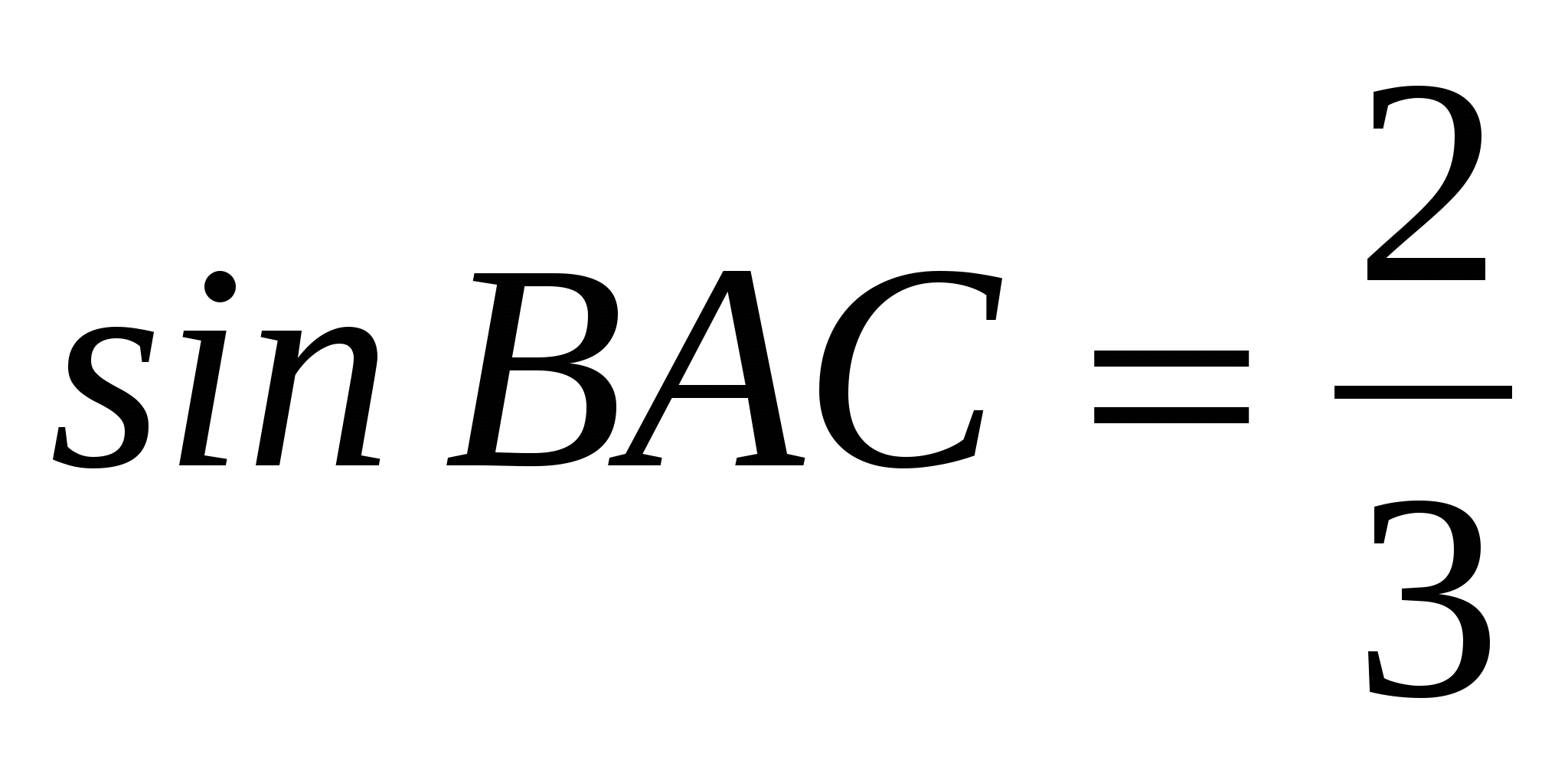 . Найдите BH. . Найдите BH.
|
30
|
26
|
В ABC 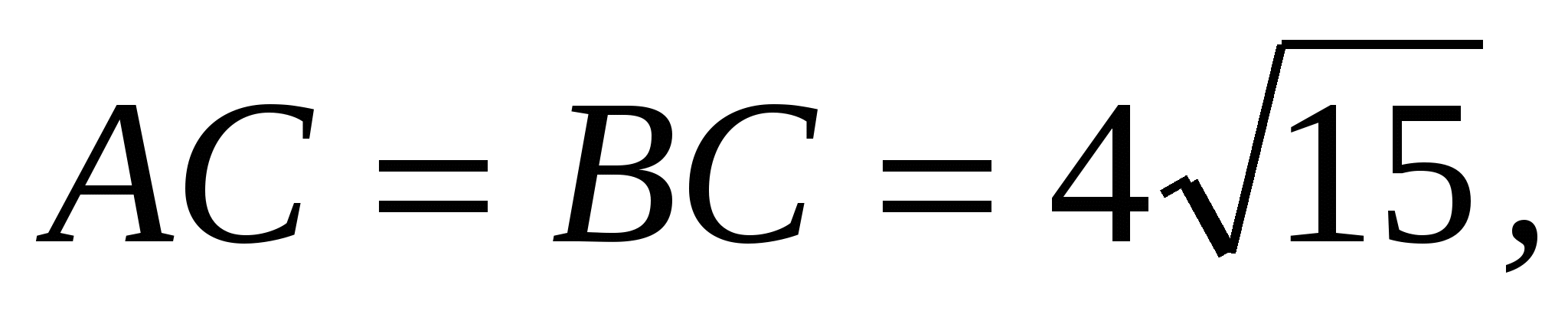 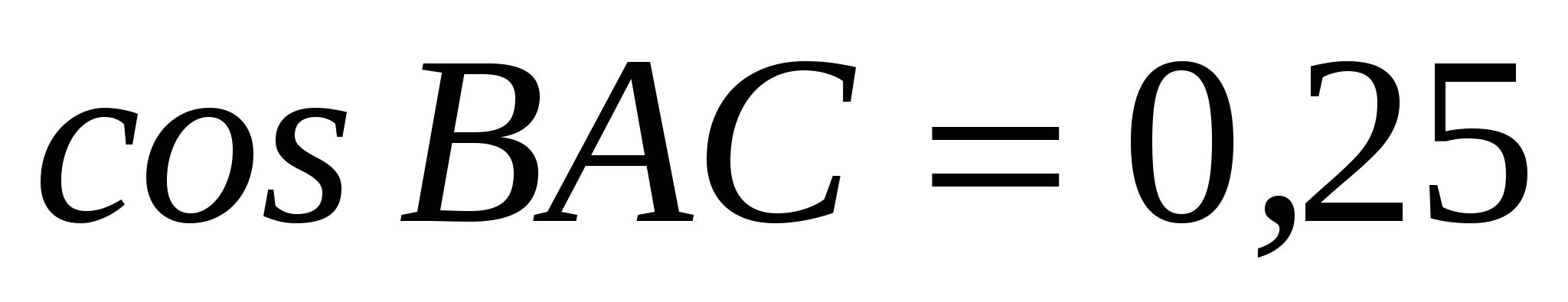 . Найдите высоту AH. . Найдите высоту AH.
|
7,5
|
27
|
В ABC AC = BC = 27, AH — высота,  . Найдите BH. . Найдите BH.
|
24
|
28
|
В ABC C = 900, CH — высота, BC= 8, BH = 4. Найдите 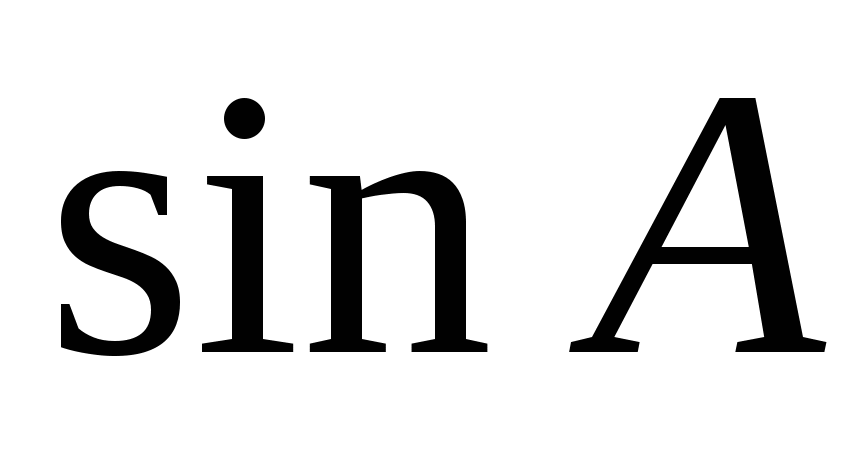 . .
|
0,5
|
29
|
В ABC C = 900, CH — высота, BC=25, BH=20. Найдите  . .
|
0,6
|
30
|
В ABC C = 900, CH — высота, 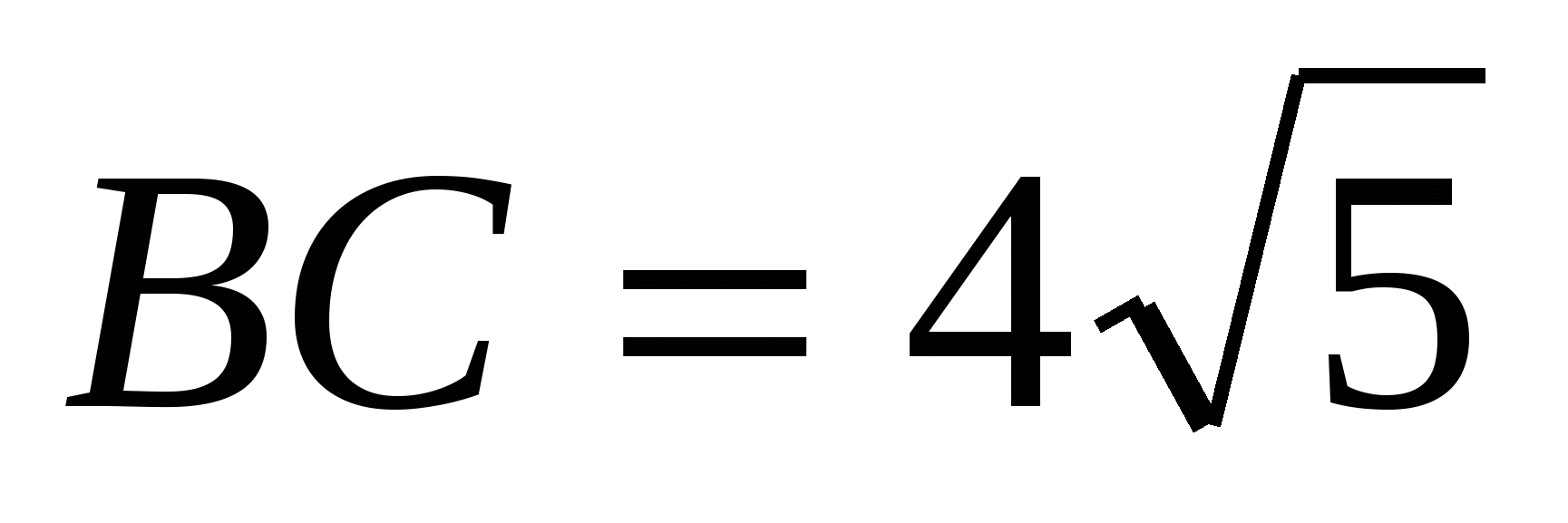 , BH = 4. Найдите , BH = 4. Найдите  . .
|
0,5
|
31
|
В ABC C = 900, высота CH равна 20, BC = 25. Найдите 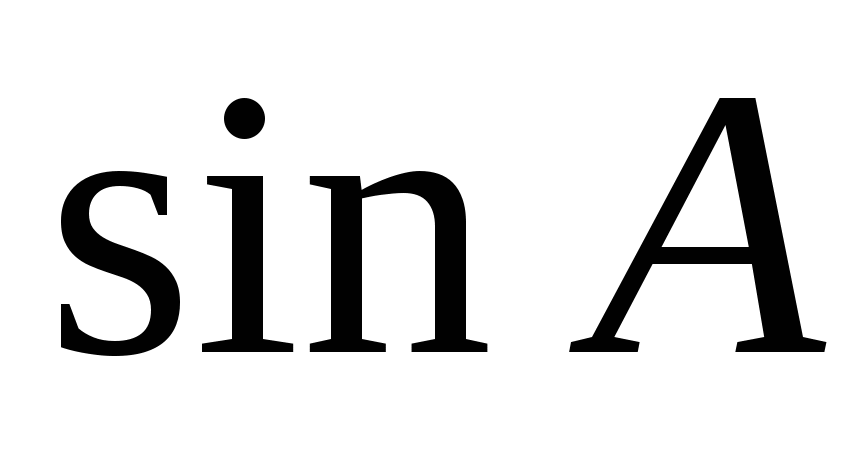 . .
|
0,6
|
32
|
В ABC C = 900, высота CH равна 4, BC = 8. Найдите  . .
|
0,5
|
33
|
В ABC C = 900, высота CH равна 4, 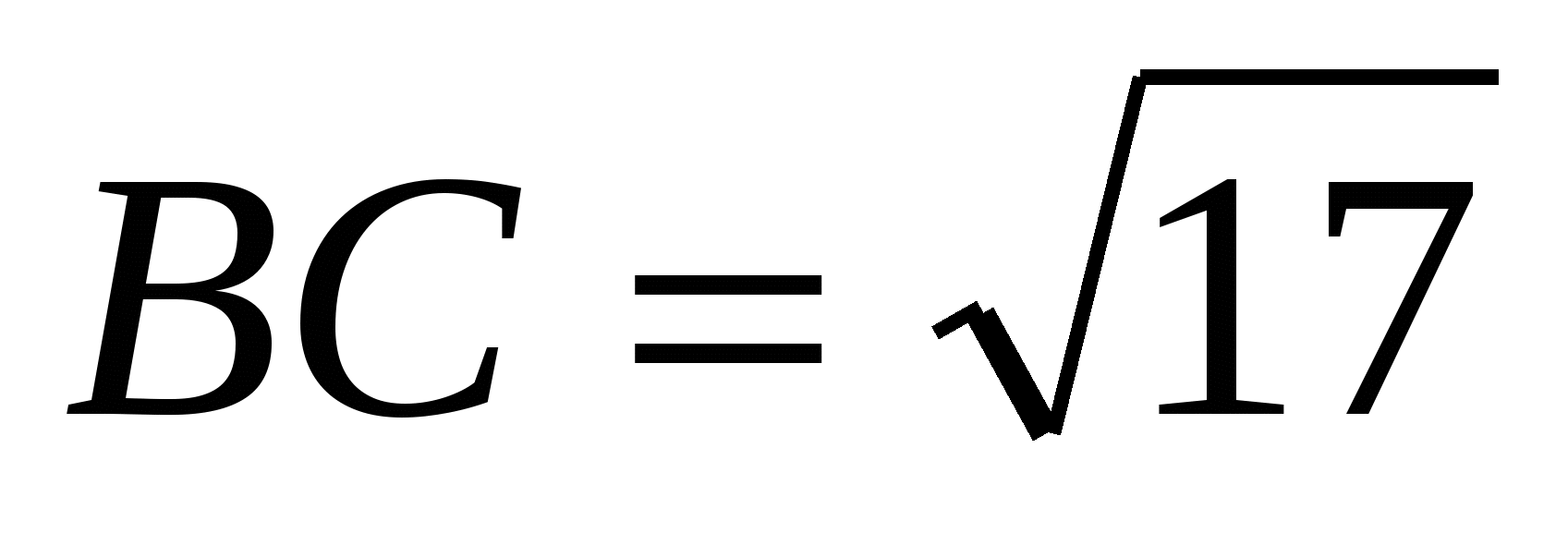 . Найдите . Найдите  . .
|
0,25
|
34
|
В ABC C = 900, высота CH равна 24, BH = 7. Найдите 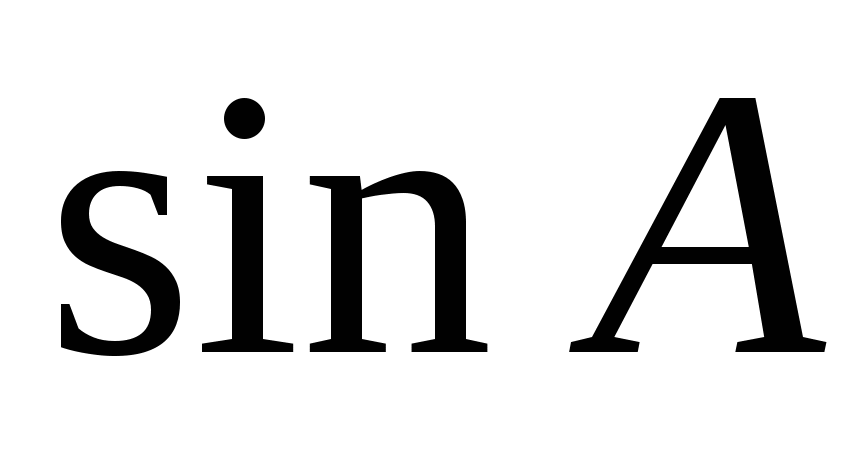
|
0,28
|
35
|
В ABC C = 900, высота CH равна 7, BH = 24. Найдите  . .
|
0,28
|
36
|
В ABC C = 900, высота CH равна 8, BH = 4. Найдите  . .
|
0,5
|
37
|
В тупоугольном ABC AC = BC = 8, высота AH равна 4. Найдите 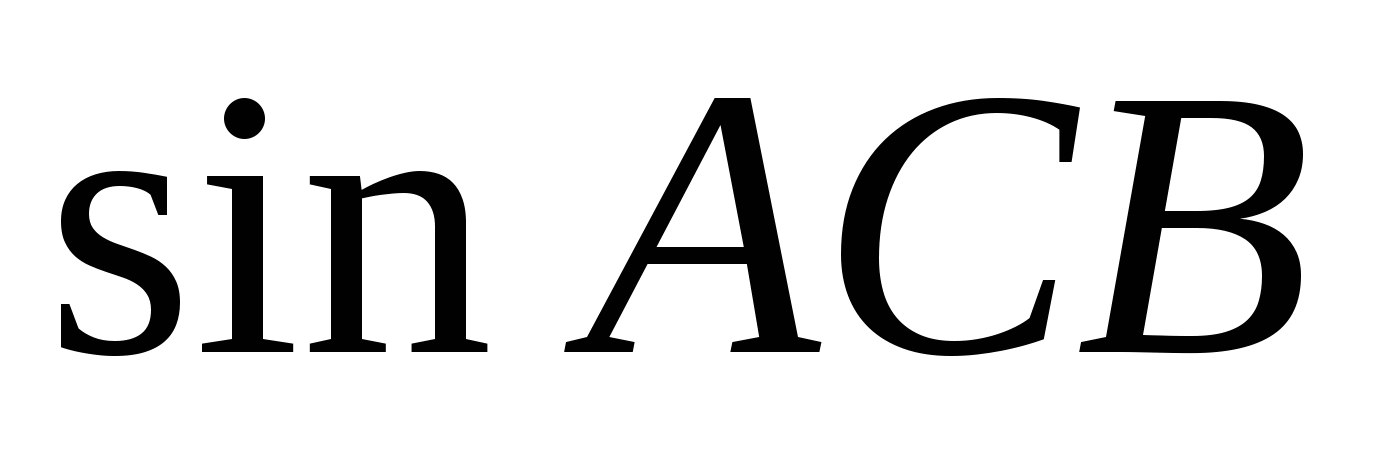 . .
|
0,5
|
38
|
В тупоугольном ABC AC = BC = 25, высота AH равна 20. Найдите 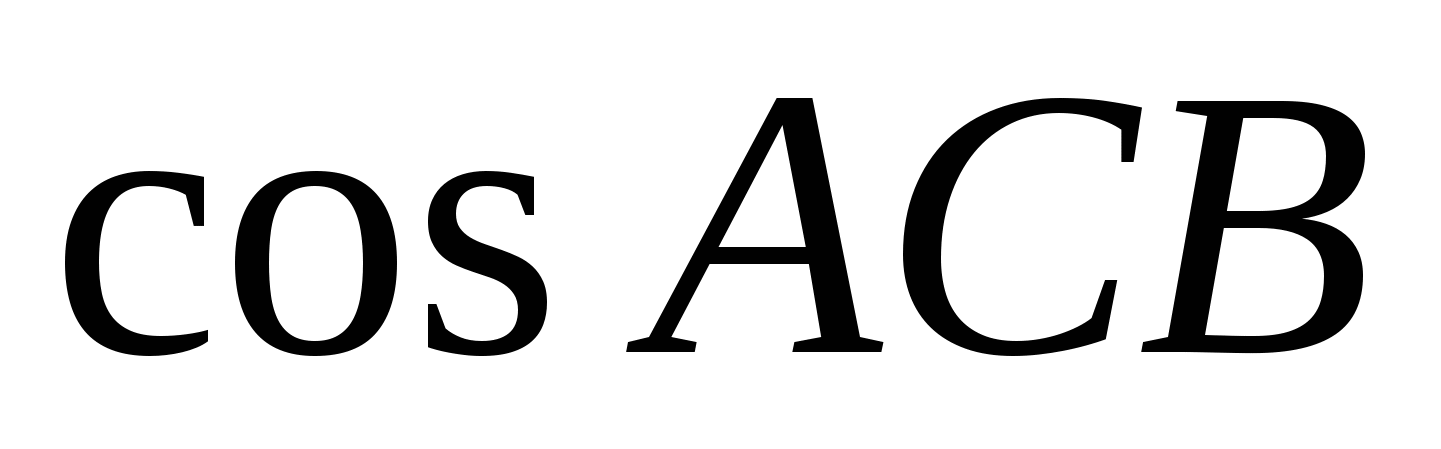 . .
|
-0,6
|
39
|
В тупоугольном ABC  , высота AH равна 4. Найдите , высота AH равна 4. Найдите 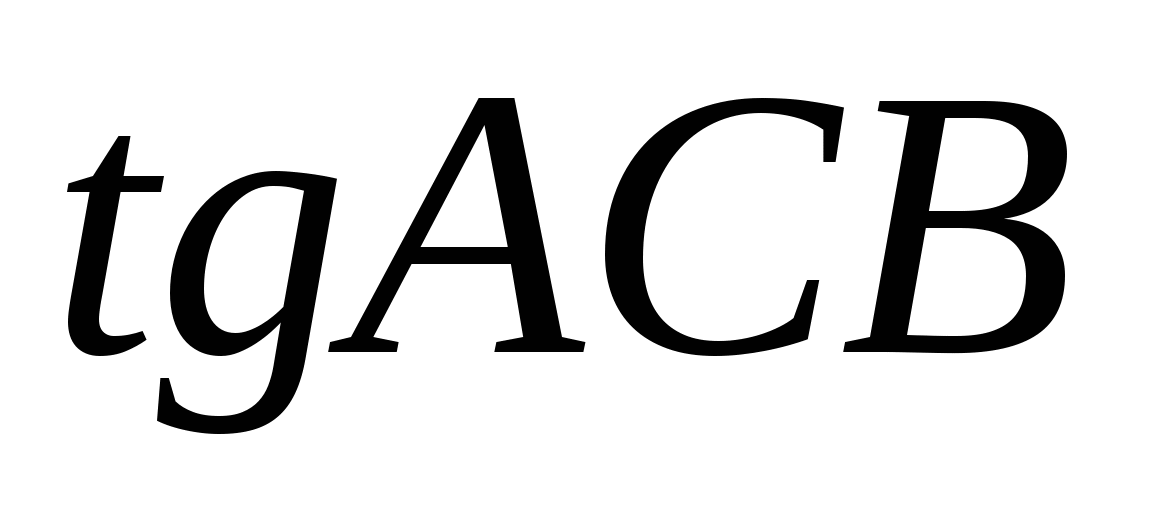 . .
|
-0,5
|
40
|
В тупоугольном ABC AC = BC = 8, AH — высота, CH = 4. Найдите 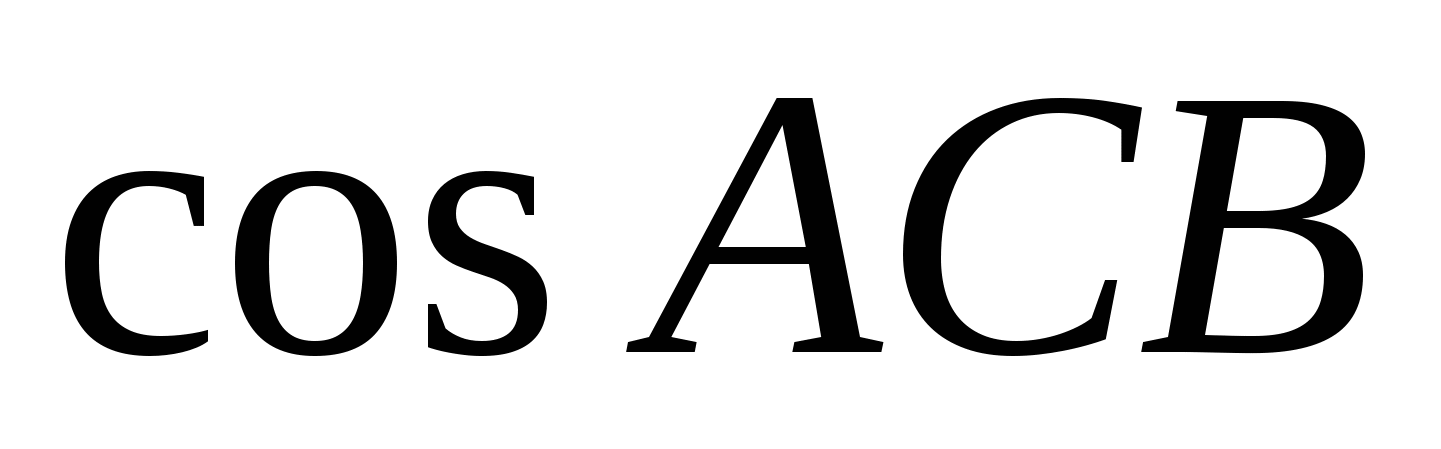 . .
|
-0,5
|
41
|
В тупоугольном ABC 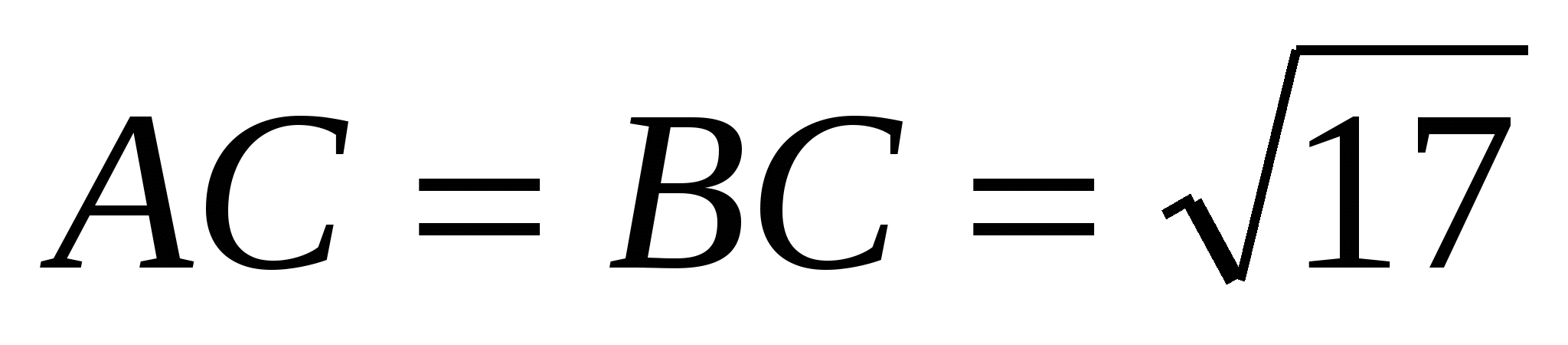 , AH — высота, CH = 4. Найдите , AH — высота, CH = 4. Найдите 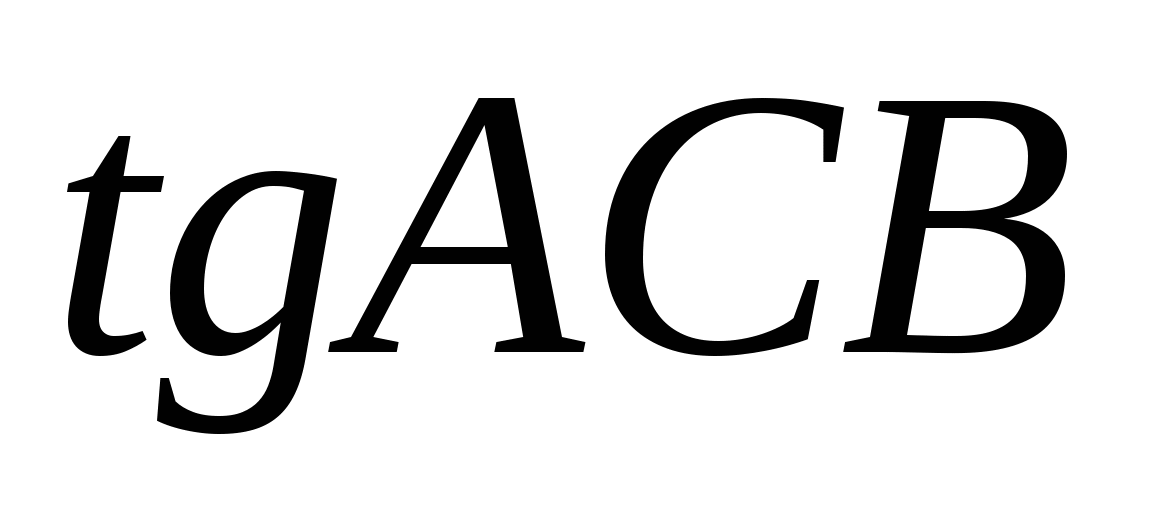 . .
|
-0,25
|
42
|
В тупоугольном ABC AC = BC, высота AH равна 7, CH = 24. Найдите 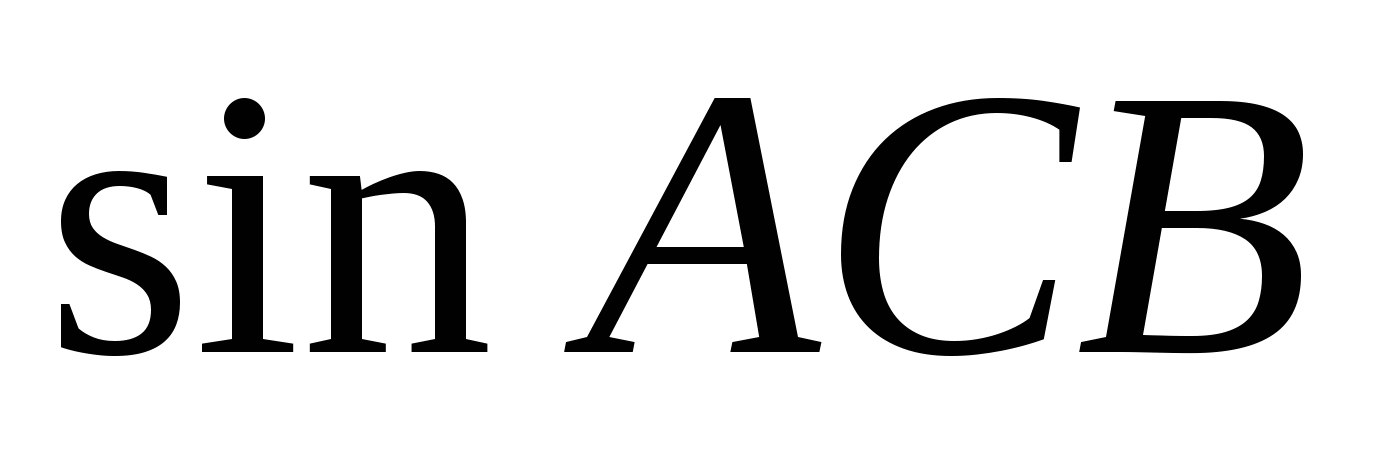 . .
|
0,28
|
43
|
В тупоугольном ABC AC = BC, высота AH равна 24, CH = 7. Найдите 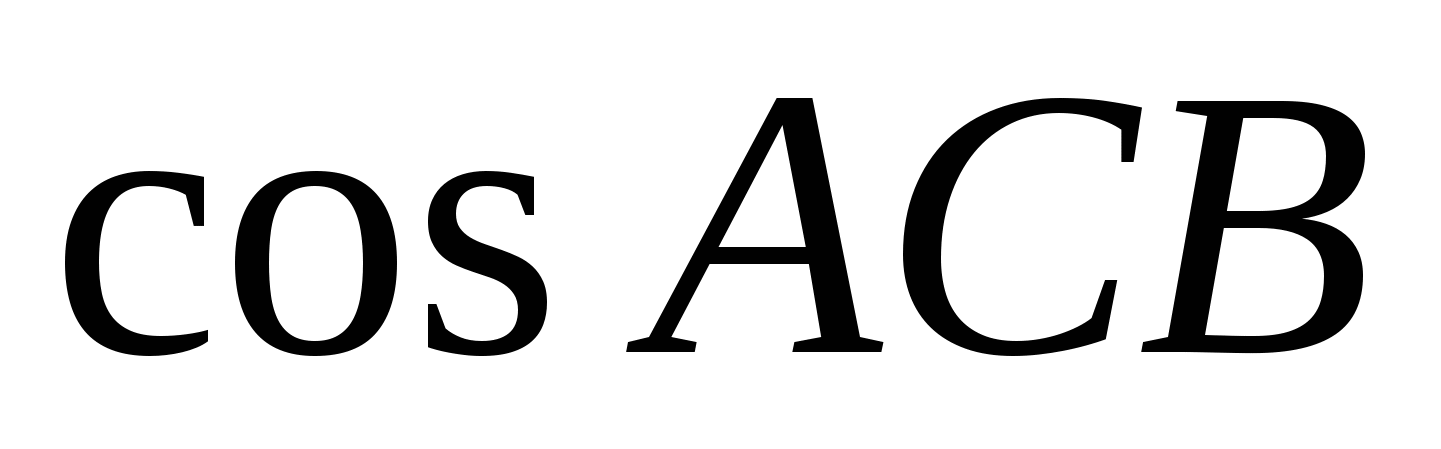 . .
|
-0,28
|
44
|
В тупоугольном ABC AC = BC, высота AH равна 4, CH = 8. Найдите 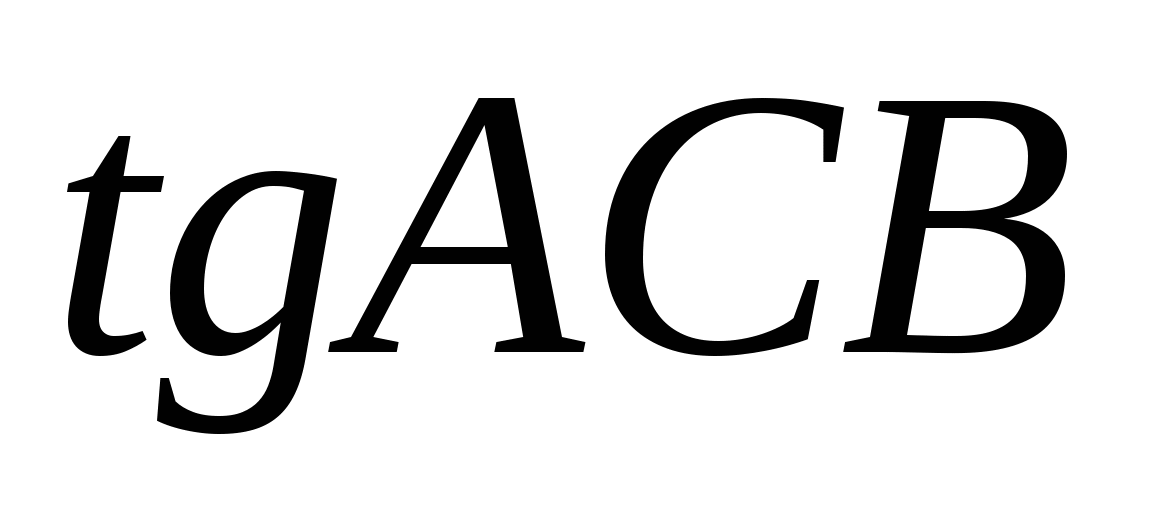 . .
|
-0,5
|
45
|
В ABC C = 900, CH — высота, AH = 27, 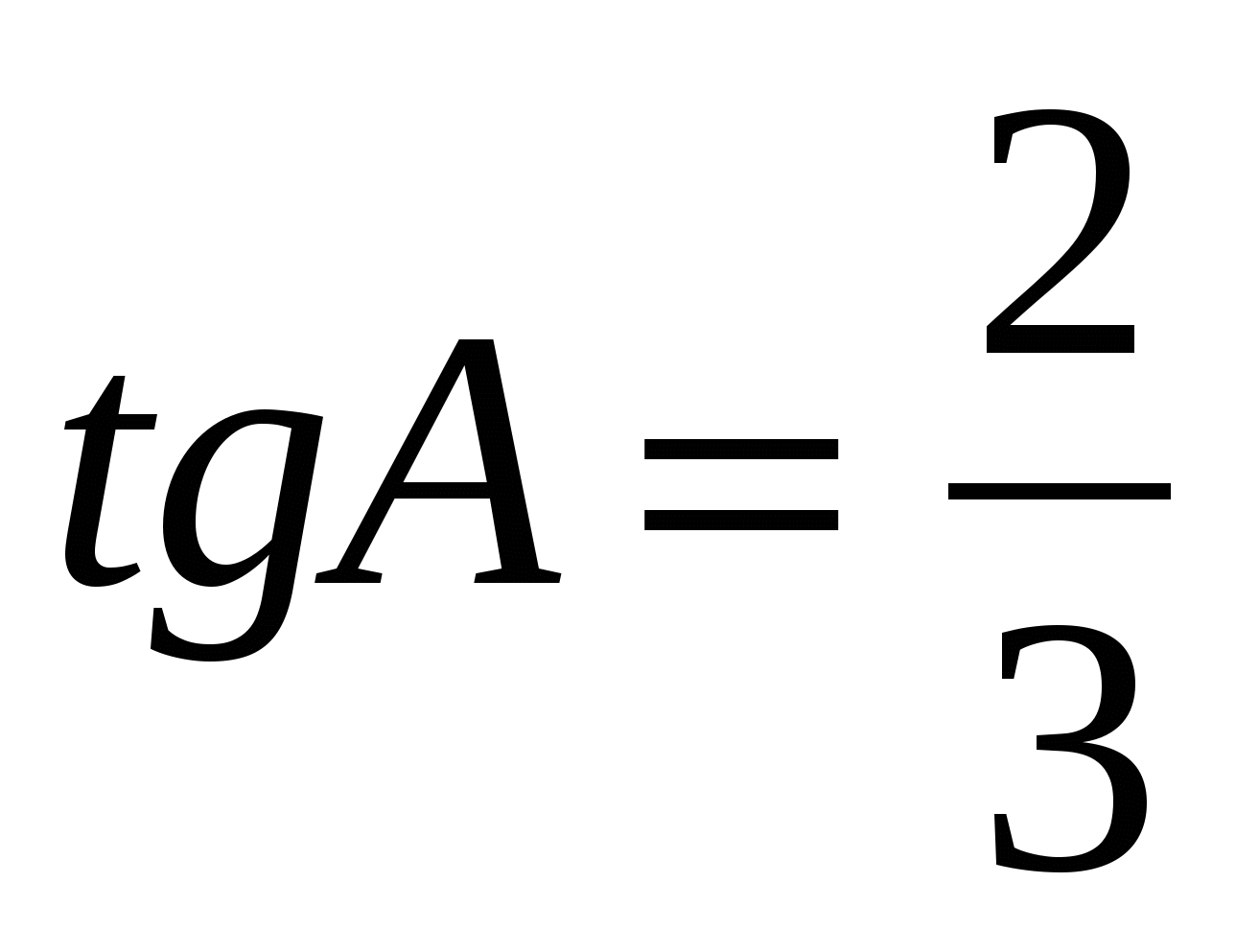 . Найдите BH. . Найдите BH.
|
12
|
46
|
В ABC C = 900, CH — высота, BH = 12, 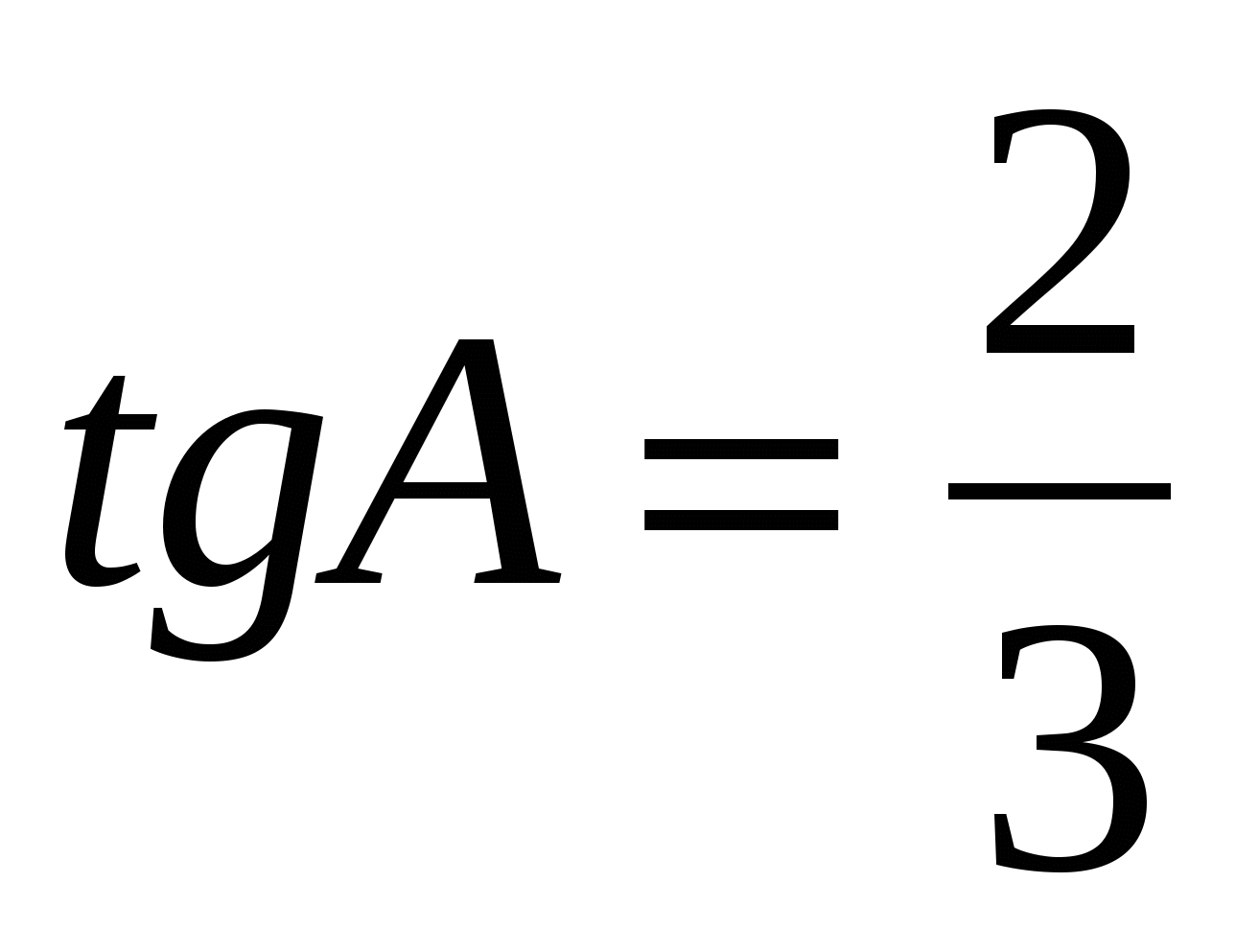 . Найдите AH. . Найдите AH.
|
27
|
47
|
В ABC C = 900, CH — высота, BH = 12, 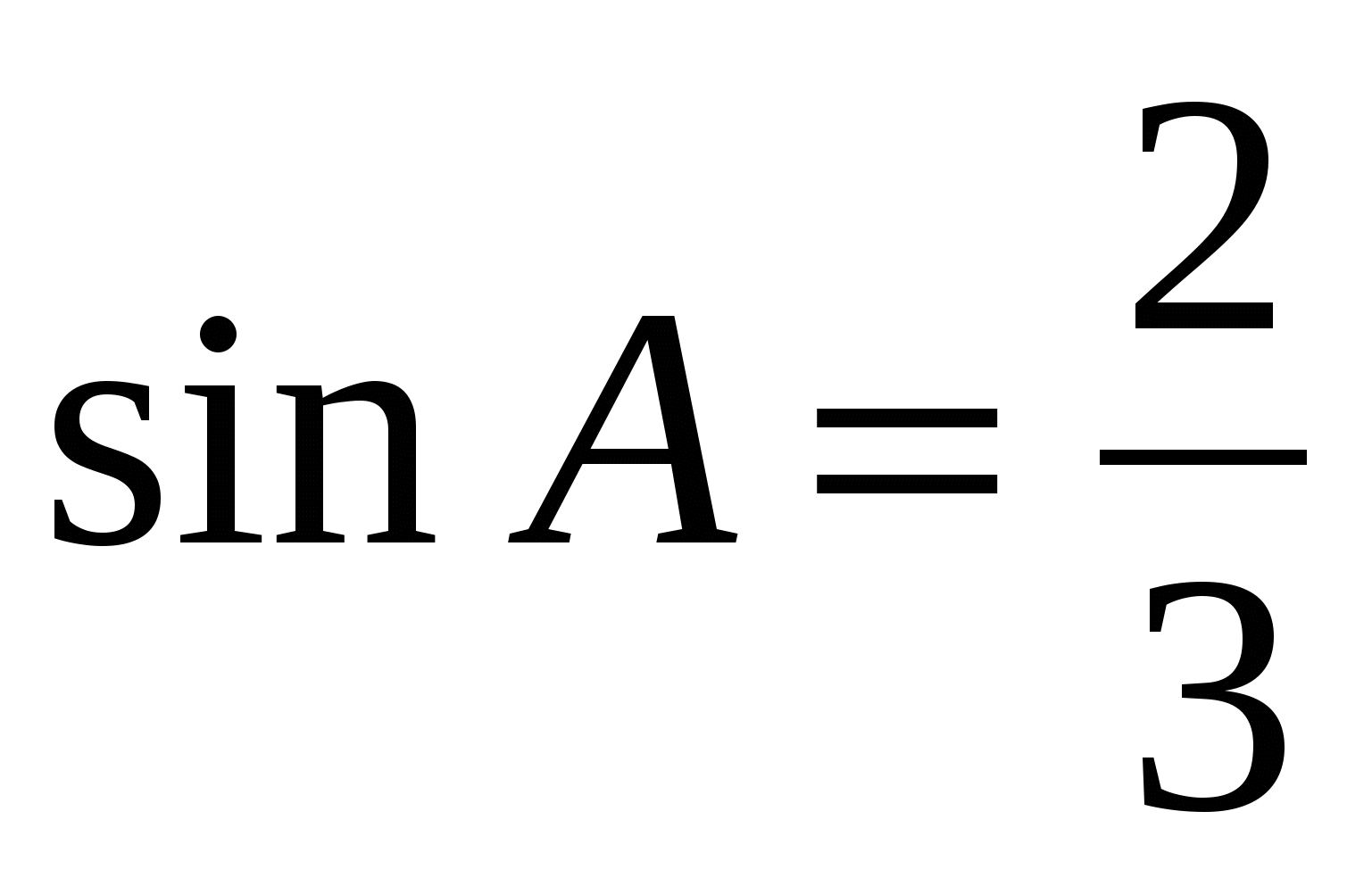 . Найдите AB. . Найдите AB.
|
27
|
48
|
В ABC C = 900, CH — высота, AH = 12, 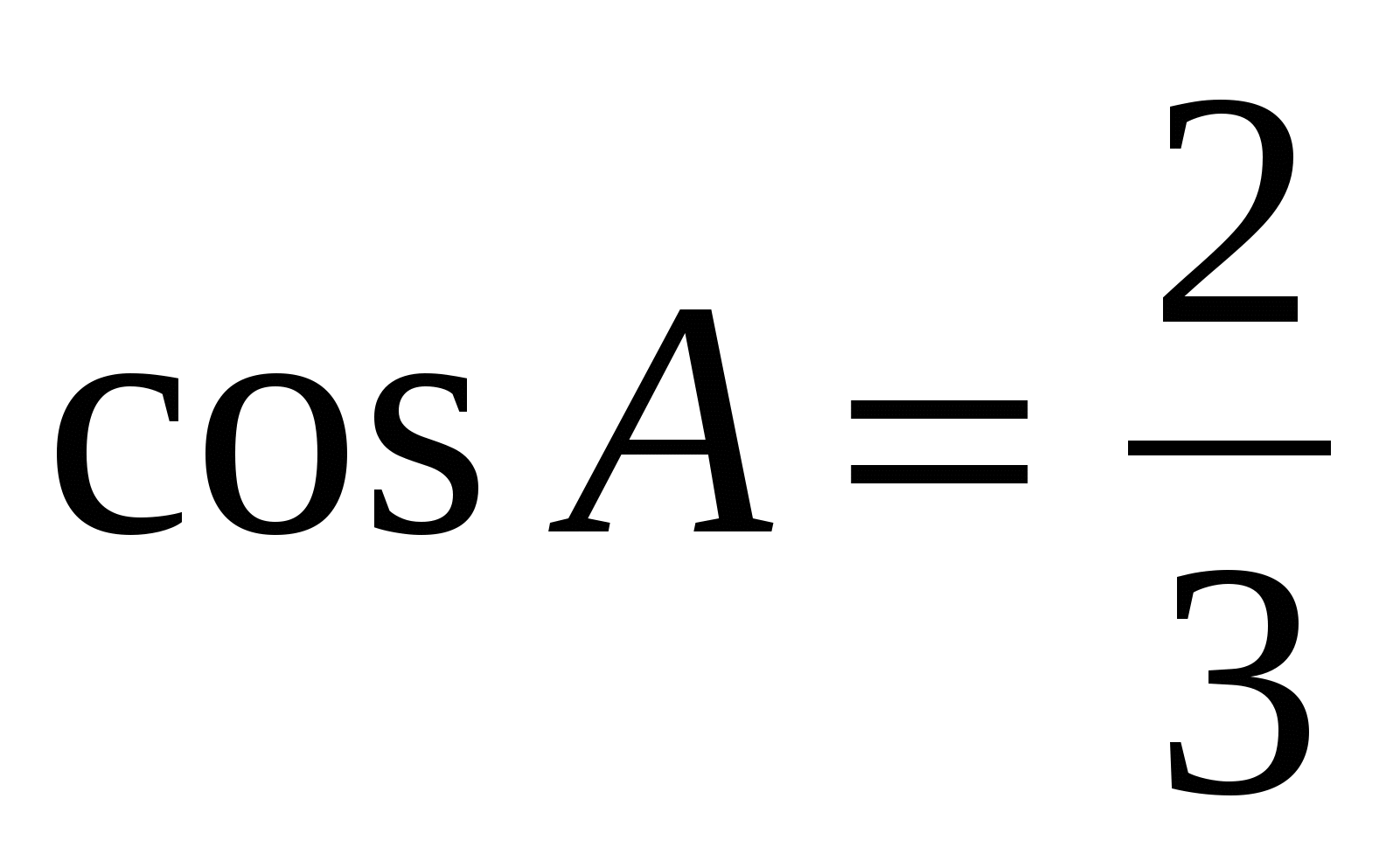 . Найдите AB. . Найдите AB.
|
27
|
49
|
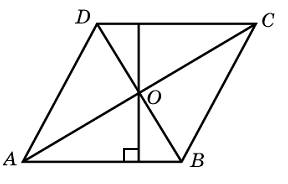
В параллелограмме ABCD AB = 3, AD = 21, 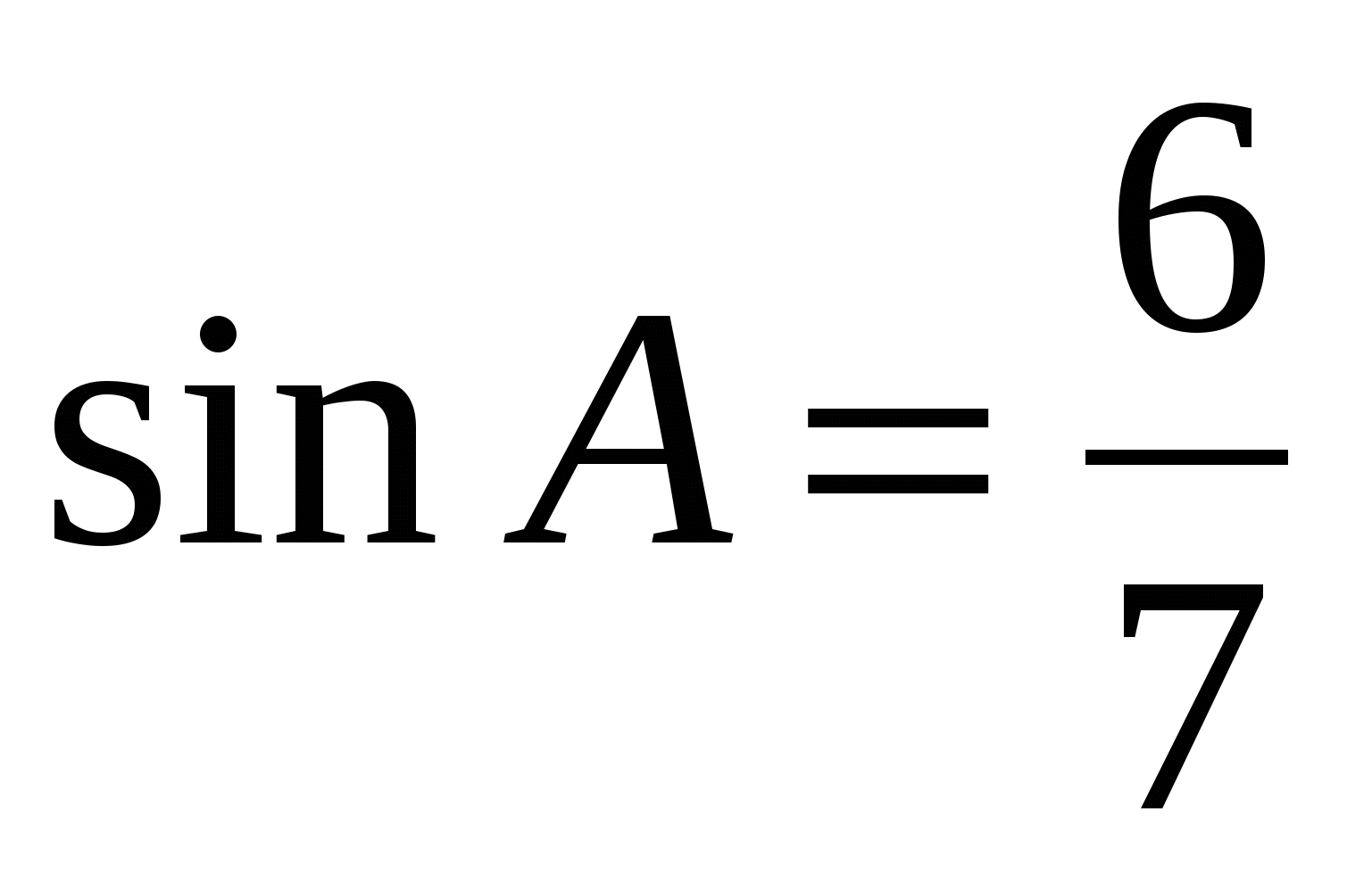 . Найдите большую высоту параллелограмма. . Найдите большую высоту параллелограмма.
|
18
|
50
|
Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.
|
0,96
|
51
|
Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен 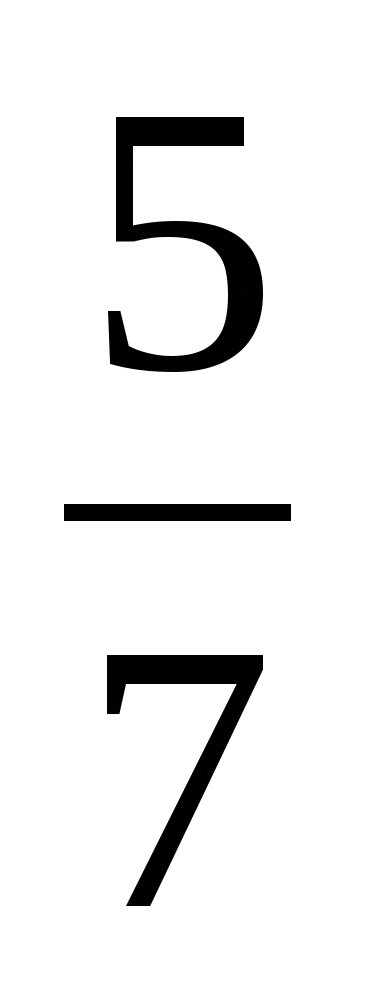 . Найдите боковую сторону. . Найдите боковую сторону.
|
21
|
52
|
Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен 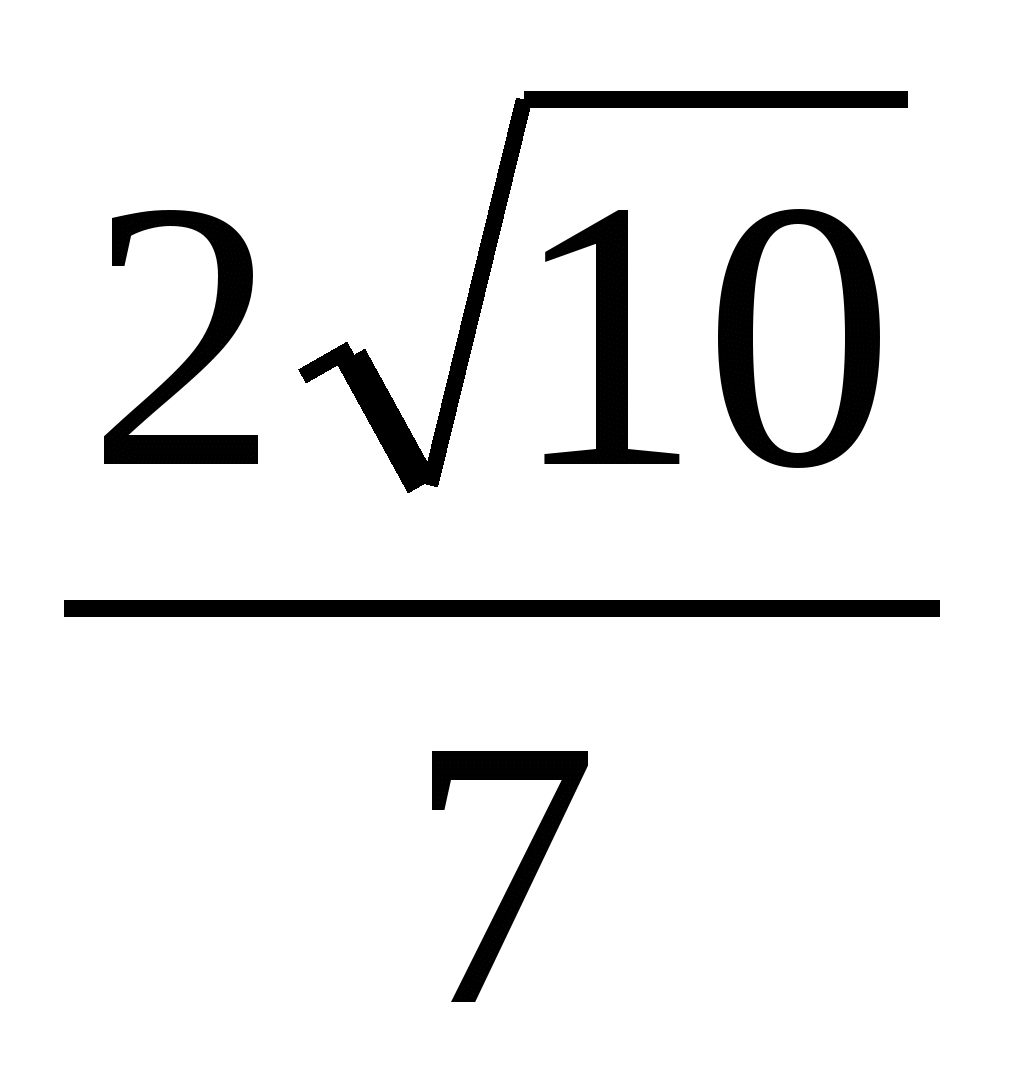 . Найдите меньшее основание. . Найдите меньшее основание.
|
22
|
53
|
Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен  . Найдите высоту трапеции. . Найдите высоту трапеции.
|
10
|
54
|
Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 39. Тангенс острого угла равен  . Найдите большее основание. . Найдите большее основание.
|
71
|
55
|
Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.
|
0,4
|
56
|
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 300. Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.
|
25
|
57
|
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 1500. Боковая сторона треугольника равна 20. Найдите площадь этого треугольника.
|
100
|
58
|
Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 300.
|
24
|
59
|
Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
|
30
|
60
|
Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.
|
6
|
61
|
Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
|
8
|
62
|
Найдите площадь ромба, если его высота равна 2, а острый угол 300.
|
8
|
63
|
Найдите площадь ромба, если его диагонали равны 4 и 12.
|
24
|
64
|
Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
|
3
|
65
|
Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.
|
2
|
66
|
Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.
|
12
|
67
|
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 300. Найдите боковую сторону треугольника, если его площадь равна 25.
|
10
|
68
|
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 1500. Найдите боковую сторону треугольника, если его площадь равна 100.
|
40
|
69
|
У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?

|
6
|
70
|
Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.

|
6
|
71
|
Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
|
160
|
72
|
Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.
|
30
|
73
|
Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 450.
|
16
|
74
|
Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах.
|
45
|
75
|
Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.
|
160
|
76
|
Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.
|
5
|
77
|
Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 1500. Найдите площадь трапеции.
|
98
|
78
|
Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.
|
30
|
79
|
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.
|
30
|
80
|
Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны 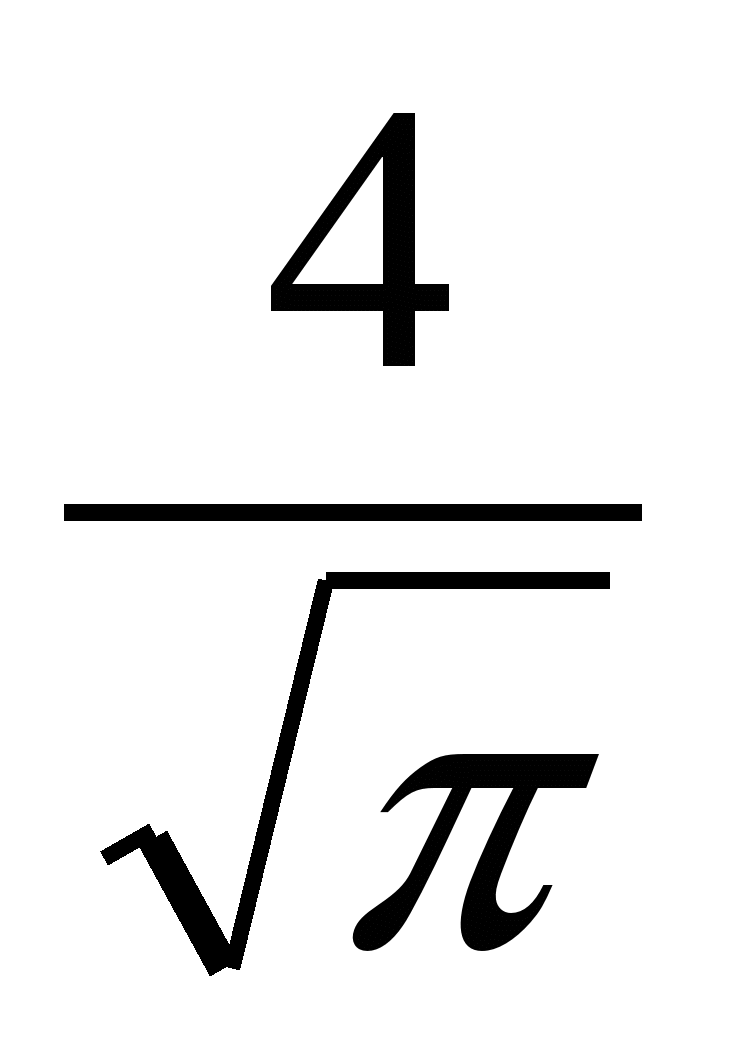 и и 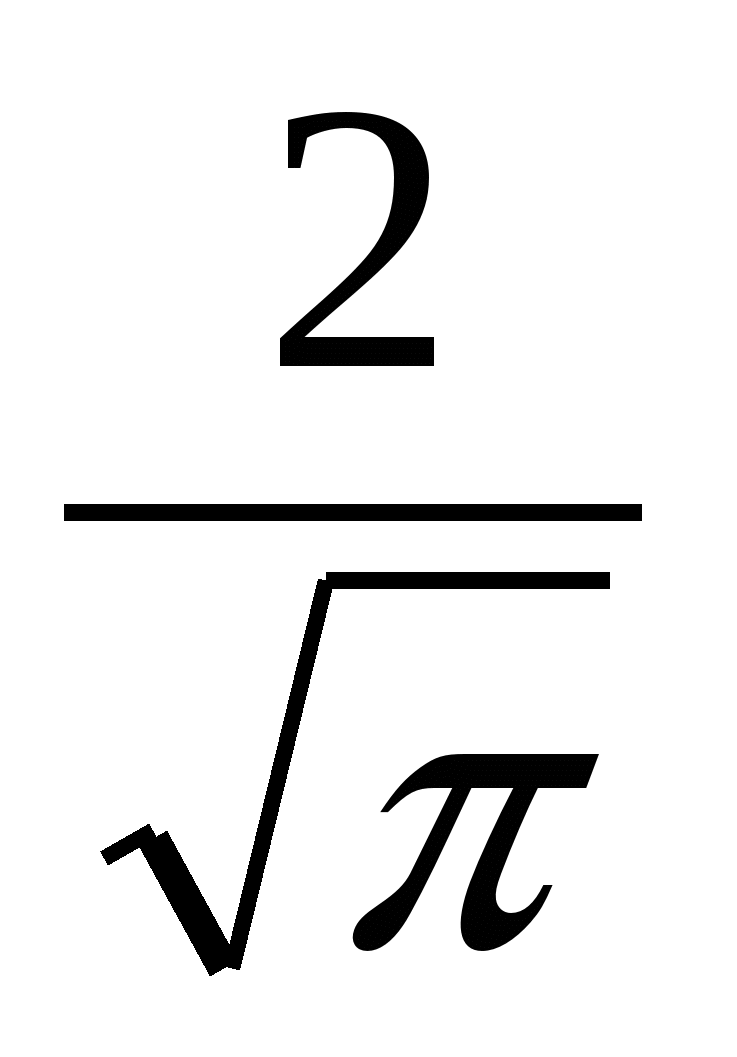 . .

|
12
|
81
|
В ABC C = 900, A = 300, 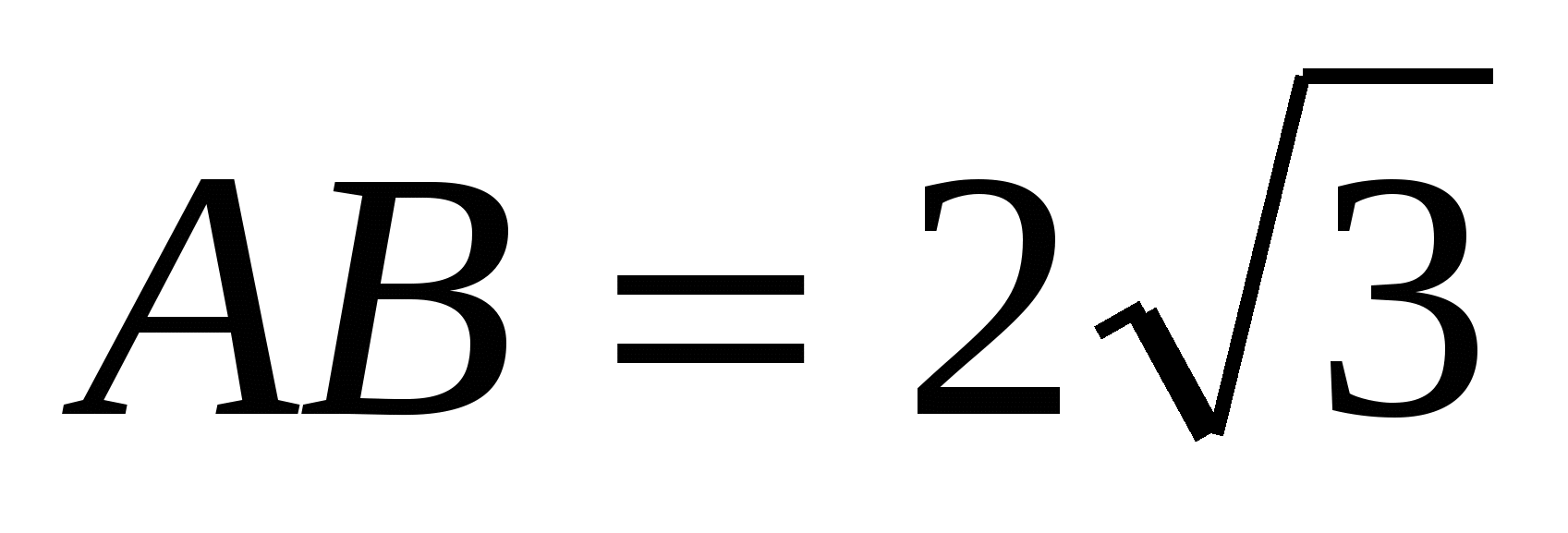 . Найдите высоту CH. . Найдите высоту CH.

|
1,5
|
82
|
В ABC C = 900, CH — высота, A = 300, AB = 2. Найдите AH. (по рис. Задачи 81)
|
1,5
|
83
|
В ABC C = 900, CH — высота, A = 300, AB = 4. Найдите BH. (по рис. Задачи 81)
|
1
|
84
|
В ABC  . Найдите высоту CH. . Найдите высоту CH.

|
3
|
85
|
В правильном ABC высота  . Найдите AB. . Найдите AB.
|
4
|
86
|
В ABC AC = BC = 4, C = 300. Найдите высоту AH.

|
2
|
87
|
В ABC AC = BC, высота AH равна 4, C =300. Найдите AC. (по рис. Задачи 87)
|
8
|
88
|
В ABC 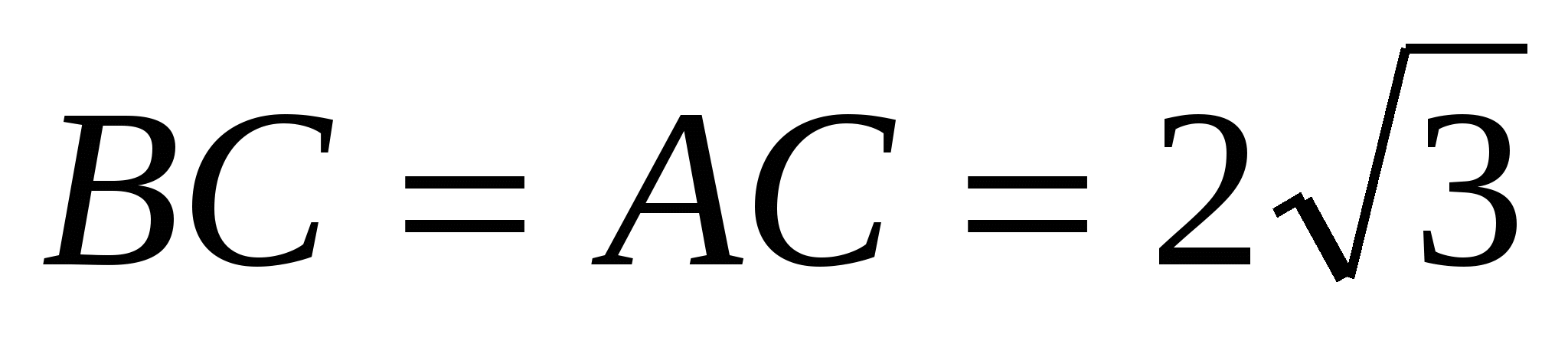 , C = 1200. Найдите высоту AH. , C = 1200. Найдите высоту AH.
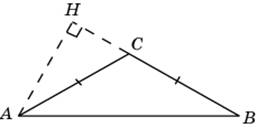
|
3
|
89
|
В ABC AC = BC, C = 1200, 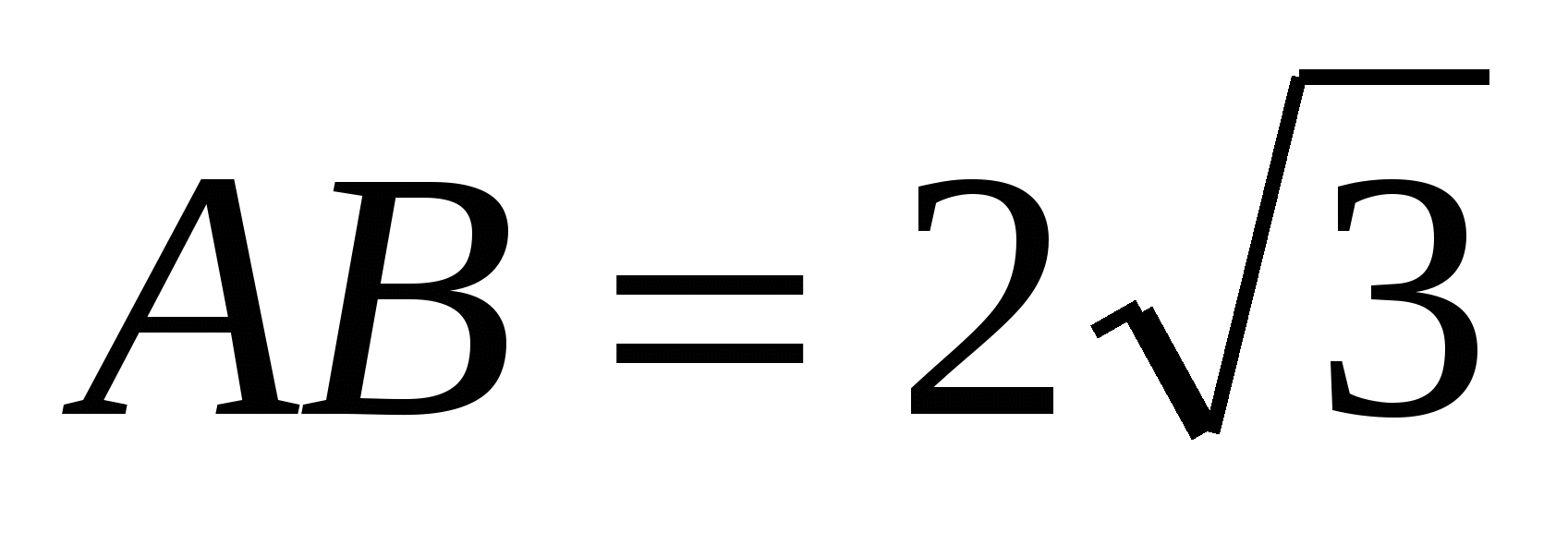 . Найдите AC. . Найдите AC.
|
2
|
90
|
В ABC AC = BC, C = 1200,  . Найдите AB. . Найдите AB.
|
6
|
91
|
Найдите высоту ромба, сторона которого равна  , а острый угол равен 600. , а острый угол равен 600.
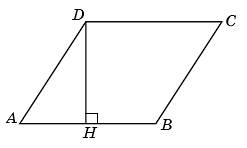
|
1,5
|
92
|
Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.
|
90
|
93
|
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4 : 3, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.

|
28
|
94
|
Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.

|
10
|
95
|
Найдите большую диагональ ромба, сторона которого равна 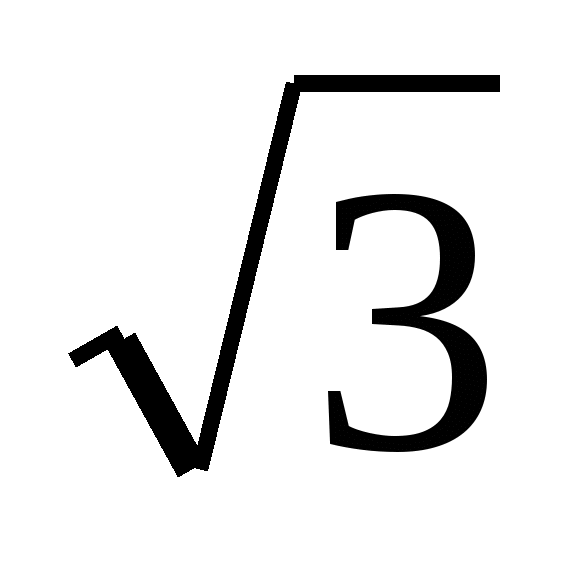 , а острый угол равен 600. , а острый угол равен 600.
|
3
|
96
|
Диагонали ромба относятся как 3 : 4. Периметр ромба равен 200. Найдите высоту ромба.
|
48
|
97
|
В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними 600. Найдите меньшее основание.
|
15
|
98
|
В равнобедренной трапеции основания равны 12 и 27, острый угол равен 600. Найдите ее периметр.
|
69
|
99
|
Основания равнобедренной трапеции равны 15 и 9, один из углов равен 450. Найдите высоту трапеции.
|
3
|
100
|
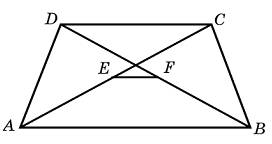
Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
|
0,5
|
101
|
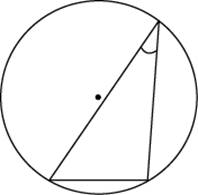
Найдите величину острого вписанного угла, опирающегося на хорду, равную радиусу окружности. Ответ дайте в градусах.
|
30
|
102
|
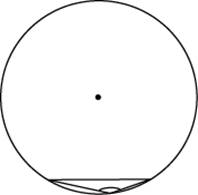
Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.
|
150
|
103
|
Найдите хорду, на которую опирается угол 1200, вписанный в окружность радиуса  . .
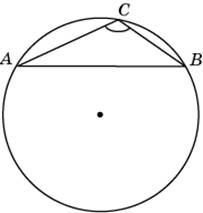
|
3
|
104
|
Найдите вписанный угол, опирающийся на дугу, длина которой равна 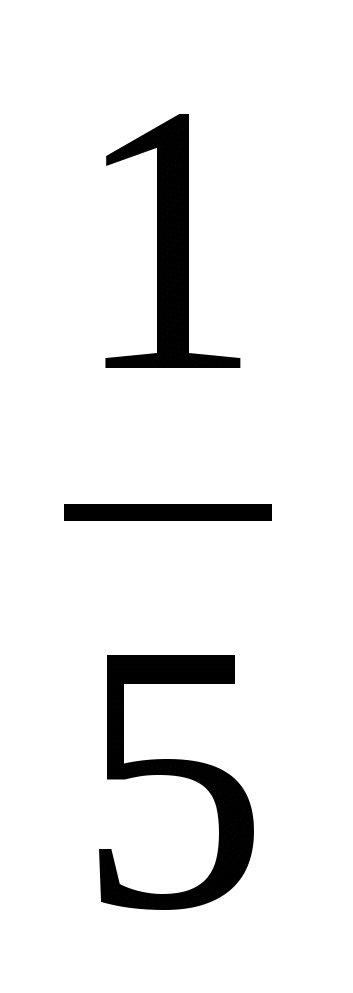 длины окружности. Ответ дайте в градусах. длины окружности. Ответ дайте в градусах.

|
36
|
105
|
Дуга окружности AC, не содержащая точки B, имеет градусную меру 2000, а дуга окружности BC, не содержащая точки A, имеет градусную меру 800. Найдите вписанный угол ACB. Ответ дайте в градусах.
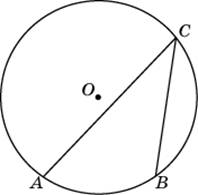
|
40
|
106
|
Хорда AB делит окружность на две дуги, градусные меры которых относятся как 5 : 7. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
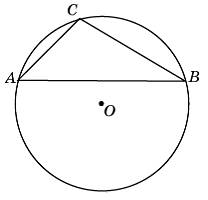
|
105
|
107
|
Точки A, B, C, расположенные на окружности, делят ее на три дуги, градусные меры которых относятся как 1 : 3 : 5. Найдите больший угол треугольника ABC. Ответ дайте в градусах.

|
100
|
108
|
AC и BD — диаметры окружности с центром O. ACB = 380. Найдите AOD. Ответ дайте в градусах.
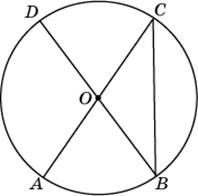
|
76
|
109
|
В окружности с центром O AC и BD — диаметры. Центральный AOD = 1100. Найдите вписанный ACB. Ответ дайте в градусах.

|
35
|
110
|
A четырехугольника ABCD, вписанного в окружность, равен 580. Найдите C этого четырехугольника. Ответ дайте в градусах.

|
122
|
111
|
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 950, 490, 710, 1450. Найдите B этого четырехугольника. Ответ дайте в градусах.

|
108
|
112
|
Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как 4 : 2 : 3 : 6. Найдите A четырехугольника ABCD. Ответ дайте в градусах.

|
60
|
113
|
Четырехугольник ABCD вписан в окружность. ABC = 1050, CAD = 350. Найдите ABD. Ответ дайте в градусах.
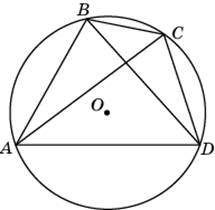
|
70
|
114
|
Четырехугольник ABCD вписан в окружность. ABD = 750, CAD = 350. Найдите ABC. Ответ дайте в градусах.
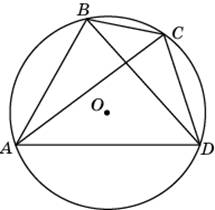
|
110
|
115
|
Четырехугольник ABCD вписан в окружность. ABC = 1100, ABD = 700. Найдите CAD. Ответ дайте в градусах.

|
40
|
116
|
Хорда AB стягивает дугу окружности в 920. Найдите ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.

|
46
|
117
|
Угол между хордой AB и касательной BC к окружности равен 320. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.
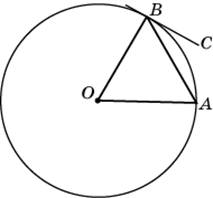
|
66
|
118
|
Через концы A, B дуги окружности в 620 проведены касательные AC и BC. Найдите ACB. Ответ дайте в градусах.
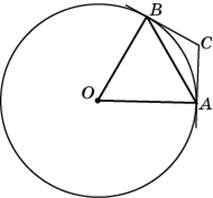
|
118
|
119
|
ACO = 240. Его сторона CA касается окружности с центром в точке O. Найдите градусную меру большей дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах.

|
114
|
120
|
Найдите ACB, если вписанные углы ADB и DAE опираются на дуги окружности, градусные меры которых равны соответственно 1180 и 380. Ответ дайте в градусах.
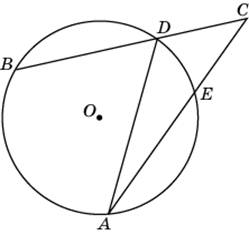
|
40
|
121
|
ACB = 420. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 1240. Найдите DAE. Ответ дайте в градусах.
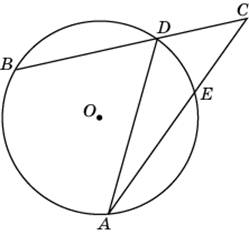
|
20
|
122
|
Найдите ABC. Ответ дайте в градусах.
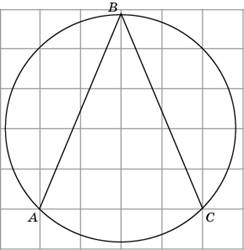
|
45
|
123
|
Найдите градусную меру дуги AC окружности, на которую опирается ABC. Ответ дайте в градусах.
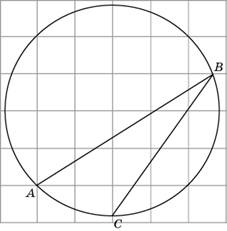
|
22,5
|
124
|
Сторона правильного треугольника равна  . Найдите радиус окружности, описанной около этого треугольника. . Найдите радиус окружности, описанной около этого треугольника.

|
1
|
125
|
Радиус окружности, описанной около правильного треугольника, равен  . Найдите сторону этого треугольника. . Найдите сторону этого треугольника.

|
3
|
126
|
Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 1200. Найдите диаметр описанной окружности этого треугольника.

|
1
|
127
|
Сторона правильного треугольника равна  . Найдите радиус окружности, вписанной в этот треугольник. . Найдите радиус окружности, вписанной в этот треугольник.

|
0,5
|
128
|
Радиус окружности, вписанной в правильный треугольник, равен 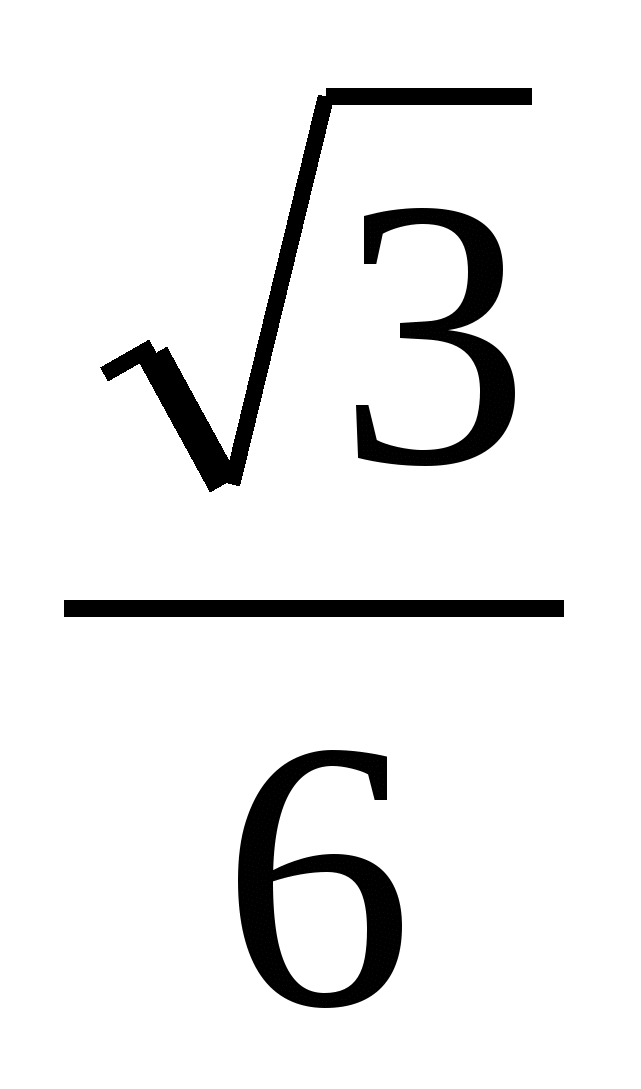 . Найдите сторону этого треугольника. . Найдите сторону этого треугольника.
|
1
|
129
|
Сторона ромба равна 1, острый угол равен 300. Найдите радиус вписанной окружности этого ромба.
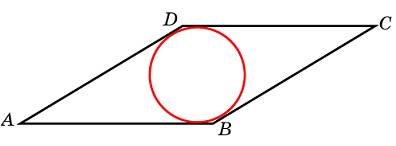
|
0,25
|
130
|
Острый угол ромба равен 300. Радиус вписанной в этот ромб окружности равен 2. Найдите сторону ромба.
|
8
|
131
|
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен  . .
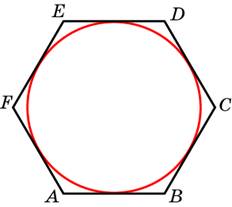
|
2
|
132
|
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной  . .
|
1,5
|
133
|
Сторона AB ABC равна 1. Противолежащий ей угол C равен 300. Найдите радиус окружности, описанной около этого треугольника.
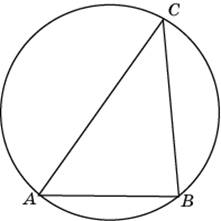
|
1
|
134
|
Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах.
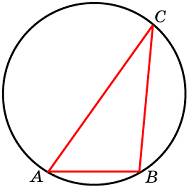
|
30
|
135
|
Угол C ABC, вписанного в окружность радиуса 3, равен 300. Найдите сторону AB этого треугольника.
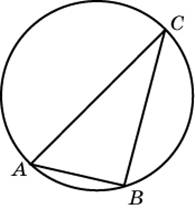
|
3
|
136
|
Сторона AB ABC равна 1. Противолежащий ей C = 1500. Найдите радиус окружности, описанной около этого треугольника.
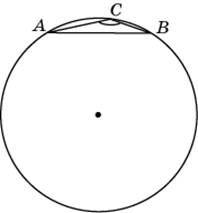
|
1
|
137
|
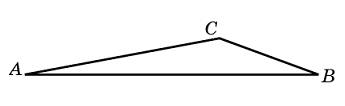
Сторона AB тупоугольного ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.
|
150
|
138
|
Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности этого треугольника.
|
25
|
139
|
Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5.
|
7
|
140
|
Два угла вписанного в окружность четырехугольника равны 820 и 580. Найдите больший из оставшихся углов. Ответ дайте в градусах.

|
122
|
141
|
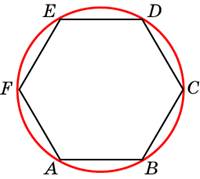
Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.
|
24
|
142
|
Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 1080. Найдите число вершин многоугольника.
|
5
|
143
|
Катеты равнобедренного прямоугольного треугольника равны 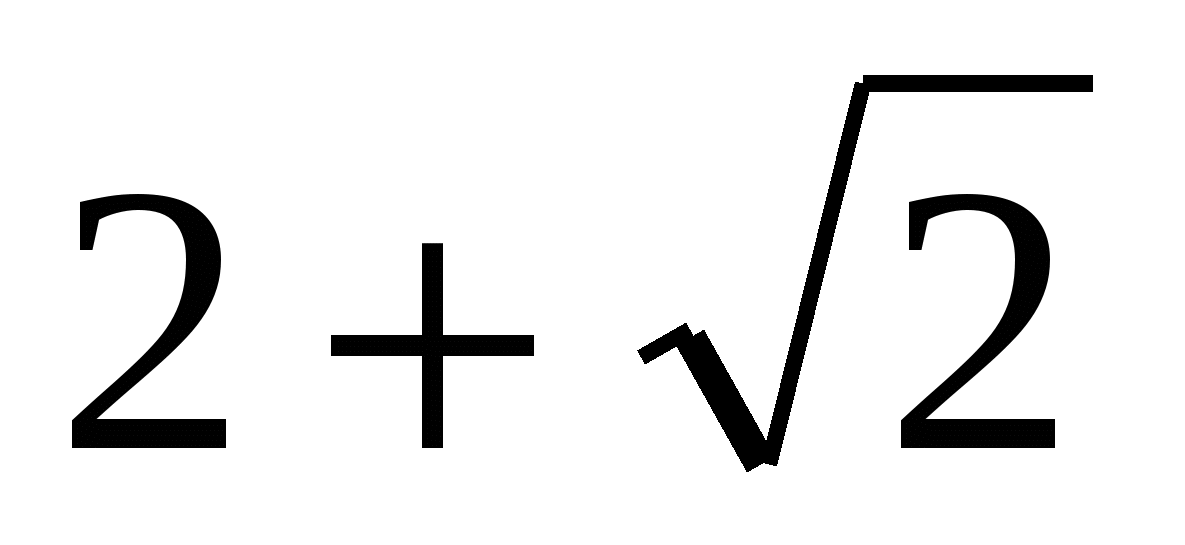 . Найдите радиус окружности, вписанной в этот треугольник. . Найдите радиус окружности, вписанной в этот треугольник.
|
1
|
144
|
В ABC AC = 4, BC = 3, C = 900. Найдите радиус вписанной окружности.
|
1
|
145
|
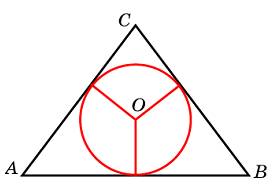
Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.
|
1,5
|
146
|
Найдите радиус окружности, вписанной в ABC, считая стороны квадратных клеток равными 1.

|
1
|
 Скачать 210.75 Kb.
Скачать 210.75 Kb.