Инструкция по выполнению работы На выполнение репетиционной экзаменационной работы по математике дается 3 часа (180 мин.). Работа состоит из двух частей и содержит 17 заданий
 Скачать 54.51 Kb. |
Математика 11 класс Вариант 4 Инструкция по выполнению работы На выполнение репетиционной экзаменационной работы по математике дается 3 часа (180 мин.). Работа состоит из двух частей и содержит 17 заданий. Часть 1 содержит 10 заданий (В1-В10) базового уровня сложности, проверяющих наличие практических математических знаний и умений. Часть 2 содержит 7 заданий (задания В11-В15 и С1-С2) повышенного и высокого уровней по материалу курса математики средней школы. Ответом к каждому из заданий В1-В15 является целое число или конечная десятичная дробь. При выполнении заданий С1-С2 требуется писать полное решение и ответ. Все бланки ЕГЭ заполняются яркими черными чернилами. Допускается использование гелевой, капиллярной или перьевой ручки. При выполнении заданий Вы можете пользоваться черновиком. Обращаем Ваше внимание, что записи в черновике не будут учитываться при оценивании работы. Советуем для экономии времени пропускать задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время. Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов. Желаем успеха!  Часть 1 Ответом на задания В1-В10 должно быть целое число или конечная десятичная дробь. Ответ следует записывать в бланк ответов №1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведенными в бланке образцами. Единицы измерений писать не нужно. В1. Спидометр автомобиля показывает скорость в милях в час. Какую скорость (в милях в час) показывает спидометр, если автомобиль движется со скоростью 56 км в час? (Считайте, что 1 миля равна 1,6 км.) Ответ:____________________ В2. При оплате услуг через платежный терминал взымается комиссия 5%. Терминал принимает суммы кратные 10 рублям. Аня хочет положить на счет своего мобильного телефона не меньше 300 рублей. Какую минимальную сумму она должна положить в приемное устройство данного терминала? 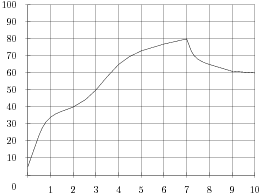 Ответ:____________________В3. На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат – температура двигателя в градусах Цельсия. Определите по графику, на сколько градусов нагреется двигатель с третьей по седьмую минуту разогрева. Ответ:_____________________ В4. В таблице даны тарифы на услуги трех фирм такси. Предполагается поездка длительностью 70 минут. Нужно выбрать фирму, в которой заказ будет стоить дешевле всего. Сколько рублей будет стоить этот заказ?
*Если поездка продолжается меньше указанного времени, она оплачивается по стоимости минимальной поездки. Ответ:______________________ В5. На клетчатой бумаге размером 1 см x 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.  Ответ:_______________________ В6. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу D. Ответ:______________________ 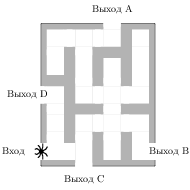 В7. Найдите корень уравнения:  .В ответе запишите наименьший положительный корень. Ответ:______________________ В 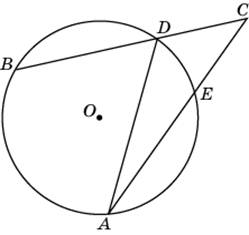 8. Найдите угол ACB, если вписанные углы ADB и DAE опираются на дуги окружности, градусные величины которых равны соответственно 118o и 38o. Ответ дайте в градусах.Ответ:______________________ В9. На рисунке изображен график производной функции f (x), определенной на интервале (- 2; 18). Найдите количество точек минимума функции f (x) на отрезке [0; 15]. 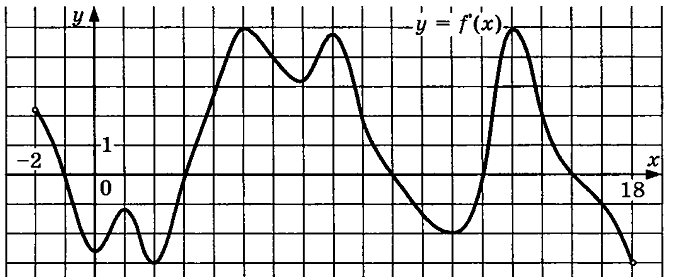 Ответ:_______________________ В10. В сосуде, имеющем форму конуса, уровень жидкости достигает 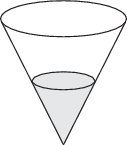 высоты.  Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?Ответ:_______________________ Не забудьте перенести все ответы в бланк ответов № 1. Часть 2 Ответом на задания В11-В15 должно быть целое число или конечная десятичная дробь. Ответ следует записывать в бланк ответов №1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно.  В11. Найдите значение выражения Ответ:______________________ В12. Трактор тащит сани с силой F=100 кН, направленной под острым углом  к гориз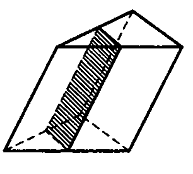онту. Работа трактора (в килоджоулях) на участке длиной S=60м вычисляется по формуле  . При каком максимальном угле (в градусах) совершенная работа будет не менее 3000 кДж?Ответ:______________________ В  13. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 12. Найдите площадь боковой поверхности исходной призмы.Ответ:_____________________ В14. Заказ на 224 детали первый рабочий выполняет на 2 часа быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 2 детали больше? Ответ:____________________ В15. Найдите точку максимума функции  Ответ:_____________________ Не забудьте перенести все ответы в бланк ответов № 1. Для записи решений и ответов на задания С1 и С2 используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем полное обоснованное решение и ответ.  С1. а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие отрезку  .С2. В основании прямой треугольной призмы  лежит прямоугольный треугольник с катетами АС = 3 и ВС = 4. Через вершину  и ребро АВ нижнего основания проведена плоскость. Найдите расстояние от вершины С до этой плоскости, если высота призмы равна 12. |