Инструкция по выполнению работы На выполнение репетиционной экзаменационной работы по математике дается 3 часа (180 мин.). Работа состоит из двух частей и содержит 17 заданий
 Скачать 56.42 Kb. |
Математика 11 класс Вариант 2 Инструкция по выполнению работы На выполнение репетиционной экзаменационной работы по математике дается 3 часа (180 мин.). Работа состоит из двух частей и содержит 17 заданий. Часть 1 содержит 10 заданий (В1-В10) базового уровня сложности, проверяющих наличие практических математических знаний и умений. Часть 2 содержит 7 заданий (задания В11-В15 и С1-С2) повышенного и высокого уровней по материалу курса математики средней школы. Ответом к каждому из заданий В1-В15 является целое число или конечная десятичная дробь. При выполнении заданий С1-С2 требуется писать полное решение и ответ. Все бланки ЕГЭ заполняются яркими черными чернилами. Допускается использование гелевой, капиллярной или перьевой ручки. При выполнении заданий Вы можете пользоваться черновиком. Обращаем Ваше внимание, что записи в черновике не будут учитываться при оценивании работы. Советуем для экономии времени пропускать задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время. Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов. Желаем успеха!  Часть 1 Ответом на задания В1-В10 должно быть целое число или конечная десятичная дробь. Ответ следует записывать в бланк ответов №1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведенными в бланке образцами. Единицы измерений писать не нужно. В1. Установка двух счётчиков воды (холодной и горячей) стоит 3700 рублей. До установки счётчиков Александр платил за воду (холодную и горячую) ежемесячно 1200 рублей. После установки счётчиков оказалось, что в среднем за месяц он расходует воды на 1000 рублей при тех же тарифах на воду. За какое наименьшее количество месяцев при тех же тарифах на воду установка счётчиков окупится? Ответ:________________________ В2. Среди 40000 жителей города 60% не интересуется футболом. Среди футбольных болельщиков 80% смотрело по телевизору финал Лиги чемпионов. Сколько жителей города смотрело этот матч? Ответ:________________________ 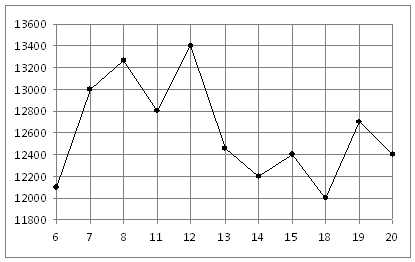 В3. На рисунке жирными точками показана цена никеля на момент закрытия биржевых торгов во все рабочие дни с 6 по 20 мая 2009 года. По горизонтали указываются числа месяца, по вертикали – цена тонны никеля в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наименьшую цену никеля на момент закрытия торгов в период с 7 по 15 мая (в долларах США за тонну).Ответ:____________________  В4. Независимая экспертная лаборатория определяет рейтинг  бытовых приборов на основе коэффициента ценности, равного 0,01 средней цены  , показателей функциональности  , качества  и дизайна  . Каждый из показателей оценивается целым числом от 0 до 4. Итоговый рейтинг вычисляется по формуле В таблице даны средняя цена и оценки каждого показателя для нескольких моделей электрических мясорубок. Определите наивысший рейтинг представленных в таблице моделей электрических мясорубок.
Ответ:______________________ В5. На клетчатой бумаге размером 1 см x 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. 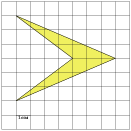 Ответ:______________________ В6. В сборнике билетов по математике всего 20 билетов, в 11 из них встречается вопрос по логарифмам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по логарифмам. Ответ:_______________________ 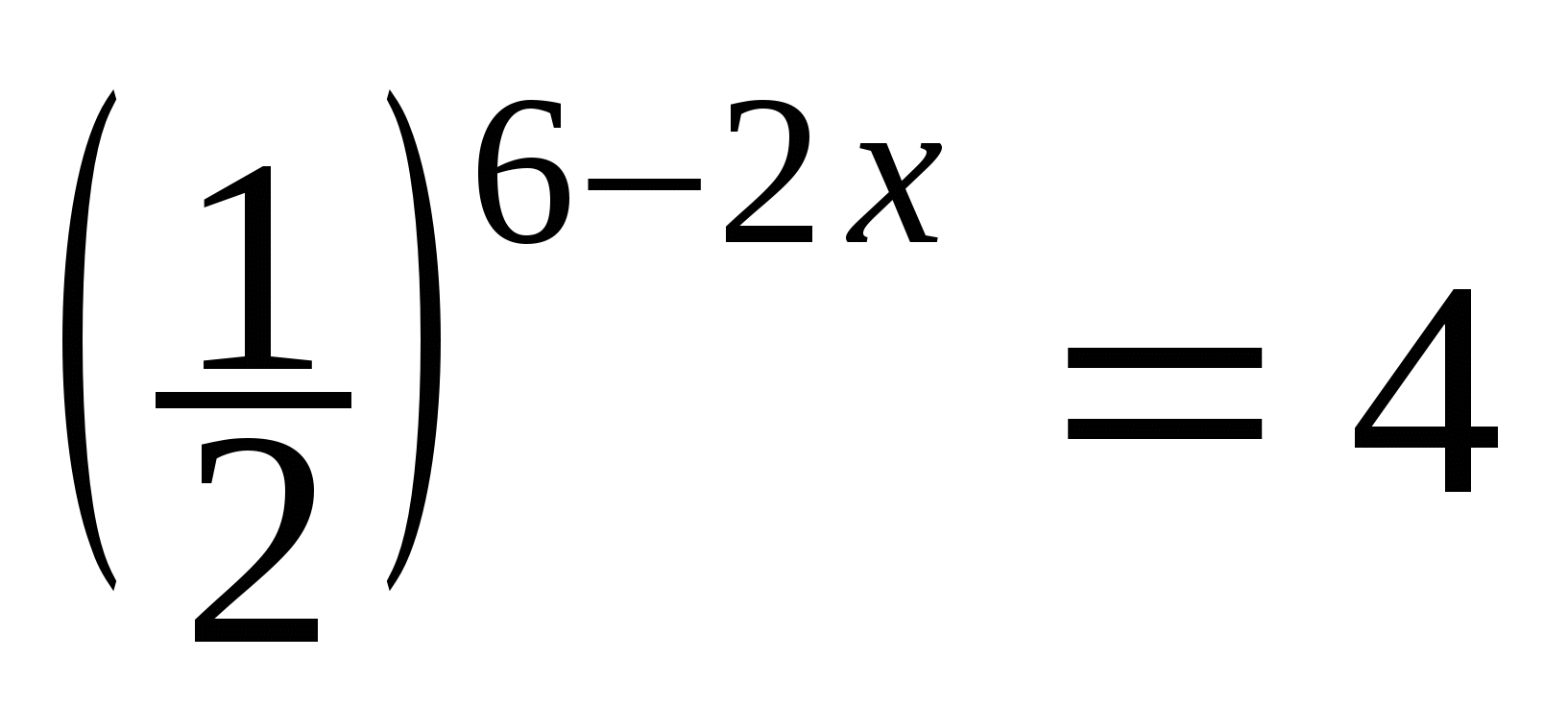 В7. Найдите корень уравнения Ответ:__________________ В8. В тупоугольном треугольнике ABC AC = BC = 25, AH – высота, CH = 20. Найдите sinACB. Ответ:___________________ В9. На рисунке изображён график функции у = f(х) и десять точек на оси абсцисс: х1, х2, х3, …, х10. В скольких из этих точек производная функции f(х) отрицательна? 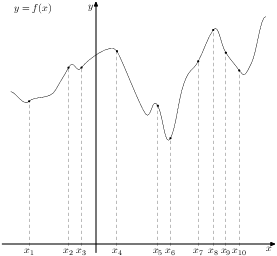 Ответ:______________________ В 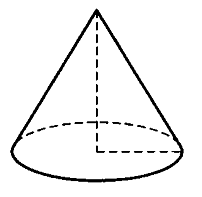 10. Во сколько раз увеличится объем конуса, если радиус его основания увеличить в 1,5 раза?Ответ:_______________________ Не забудьте перенести все ответы в бланк ответов № 1. Часть 2 Ответом на задания В11-В15 должно быть целое число или конечная десятичная дробь. Ответ следует записывать в бланк ответов №1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно.  В11. Найдите значение выражения Ответ____________________________ В12. Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной  км с постоянным ускорением  км/ч², вычисляется по формуле  . Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав 0,4 километра, приобрести скорость не менее 160 км/ч. Ответ выразите в км/ч². Ответ:_________________________ В 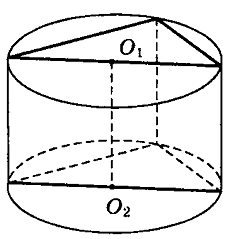 13. В основании прямой призмы лежит прямоугольный треугольник с катетами 10 и 9. Боковые ребра равны  . Найдите объем цилиндра, описанного около этой призмы.Ответ:____________________ В14. Теплоход проходит по течению реки до пункта назначения 352 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 3 км/ч, стоянка длится 6 часов, а в пункт отправления теплоход возвращается через 44 часа после отплытия из него. Ответ дайте в км/ч. Ответ:___________________  В15. Найдите точку минимума функции Ответ:___________________ Не забудьте перенести все ответы в бланк ответов № 1. Для записи решений и ответов на задания С1 и С2 используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем полное обоснованное решение и ответ.  С1. а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие отрезку  С2. В прямоугольном параллелепипеде  ребра  ,  . Найдите расстояние от вершины А до диагонали  боковой грани. |