|
Денисова Оксана Александровна 2011-2012 учебный год пояснительная записка
Муниципальное общеобразовательное учреждение «Лицей №5» г. Губкин Белгородской области
Рассмотрено Согласовано: Утверждаю:
на заседании МО учителей заместитель директора по УВР директор МОУ «Лицей №5»
математики, физики, информатики МОУ «Лицей №5» г. Губкин г. Губкин
МОУ «Лицей №5» г. Губкин __________ Просветова Ж.А. _______________ Сергеев Н.И.
Руководитель МО «____» ____________ 2011г. Приказ № «_____» от
__________ Шевцова Т.В. «____» _____________ 2011г.
Протокол № ____ от
«____» ___________ 2011 г.
Рабочая программа по алгебре
для 8 а класса
(углубленное изучение)
Автор - составитель Рабочей программы: учитель математики Денисова Оксана Александровна
2011-2012 учебный год
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Настоящая программа по алгебре для основной общеобразовательной школы 8 класса составлена на основе федерального компонента государственного стандарта основного общего образования (приказ МОиН РФ от 05.03.2004г. № 1089), примерных программ по математике (письмо Департамента государственной политики в образовании Минобрнауки России от 07.07.2005г. № 03-1263), «Временных требований к минимуму содержания основного общего образования» (приказ МО РФ от 19.05.98. № 1236), программы для общеобразовательных учреждений. Планирование учебного материала. Алгебра 7–9 классы. Автор составитель И.Е. Феоктистов. – М.: Мнемозина, 2010г. с. 20. При составлении рабочей программы учтены рекомендации инструктивно-методического письма «О преподавании математики в 2011-2012 учебном году в общеобразовательных учреждениях Белгородской области»
Цели и задачи:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;
развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов (физика, химия, основы информатики и вычислительной техники), усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач, осуществление функциональной подготовки школьников. В ходе изучения курса учащиеся овладевают приёмами вычислений на калькуляторе.
Рабочая программа обеспечена учебно – методическим комплексом, учрежденным приказом Минобрнауки РФ, используемого для достижения поставленной цели в соответствии с образовательной программой учреждения.
Перечень учебно – методических средств обучения:
1. Алгебра. 8 класс : учеб. для общеобразоват. учреждений /Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов. – 7-е изд., испр. и доп. – М.Мнемозина, 2008.-384с.
2. Алгебра. 8 класс. Дидактические материалы. Методические рекомендации / И.Е. Феоктистов.- М.:Мнемозина, 2011.-173с.
Рабочая программа рассчитана на 175часов (5 часов в неделю), в т.ч. 7 часов отведено на проведение контрольных работ и 24 часа на проведение самостоятельных работ, согласно инструктивно – методическому письму «О преподавании математики в 2011-2012 учебном году в общеобразовательных учреждениях Белгородской области»
Авторская программа рассчитана на 34 учебные недели (170 часов), а в нашей рабочей программе 35 учебных недель (175 часов), 5 часов добавлены на повторение.
Требования к уровню подготовки обучающихся в 8 классе
В ходе преподавания алгебры в 8 классе, работы над формированием у обучающихся перечисленных в программе знаний и умений следует обращать внимание на то, чтобы они овладевали овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
В результате изучения курса алгебры 8 класса обучающиеся должны:
знать/понимать1
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
Арифметика
уметь
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты — в виде дроби и дробь — в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;
округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;
Алгебра
уметь
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций (у=кх, где к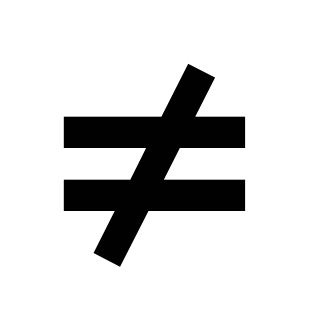 0, у=кх+b, у=х2, у=х3, у = 0, у=кх+b, у=х2, у=х3, у =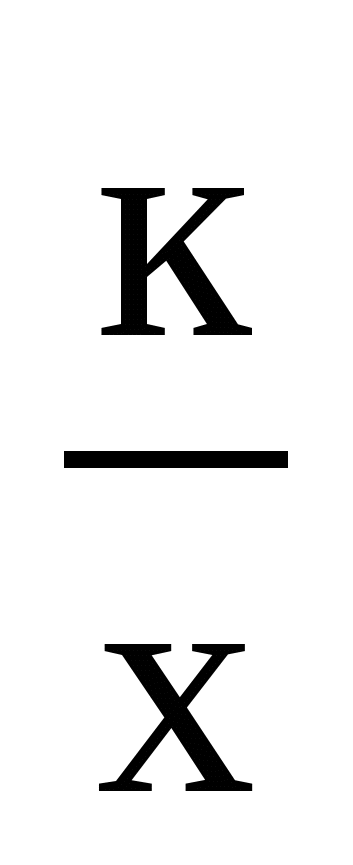 , у= , у=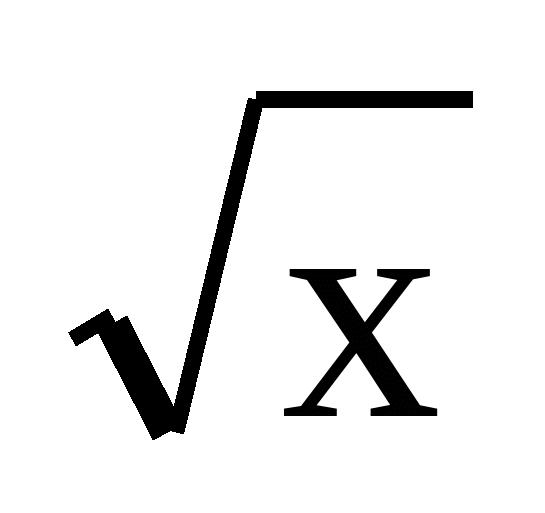 ), строить их графики; ), строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами.
Элементы логики, комбинаторики, статистики и теории вероятностей
уметь
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов, вычислять средние значения результатов измерений;
находить частоту события, используя собственные наблюдения и готовые статистические данные;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выстраивания аргументации при доказательстве (в форме монолога и диалога);
распознавания логически некорректных рассуждений;
записи математических утверждений, доказательств;
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
решения учебных и практических задач, требующих систематического перебора вариантов;
понимания статистических утверждений.
Содержание учебного курса
Арифметика
Натуральные числа. Делимость натуральных чисел. Признаки делимости на 2, 3, 4, 5, 9, 10, 11. Простые и составные числа. Бесконечность множества простых чисел. Основная теорема арифметики. Разложение натурального числа на простые множители.
Наибольший общий делитель и наименьшее общее кратное. Алгоритм Евклида.
Целые числа. Деление с остатком.
Рациональные числа. Степень с целым показателем.
Задача измерения величин. Единица измерения. Измерение отрезков: единичный отрезок, процесс измерения. Общая мера двух отрезков. Соизмеримость и несоизмеримость отрезков. Связь между соизмеримостью отрезков и отношением их длин. Несоизмеримость диагонали квадрата с его стороной.
Представление рационального числа в виде бесконечной периодической десятичной дроби. Представление бесконечной периодической десятичной дроби в виде обыкновенной.
Действительные числа. Бесконечная десятичная дробь как результат измерения отрезка. Действительные числа как бесконечные десятичные дроби. Периодические десятичные дроби. Примеры бесконечных непериодических десятичных дробей. Свойства множества действительных чисел.
Решение уравнения х2 = 2 во множестве рациональных чисел и во множестве действительных чисел.
Квадратный корень из числа. Условие существования квадратного корня и число квадратных корней из действительного числа. Арифметический квадратный корень.
Понятие об иррациональном числе. Иррациональность числа  . Десятичные приближения иррациональных чисел. Нахождение приближенного значения корня с помощью калькулятора. . Десятичные приближения иррациональных чисел. Нахождение приближенного значения корня с помощью калькулятора.
Стандартный вид числа.
Измерения, Приближения, оценки.
Алгебра
Алгебраические выражения. Свойства степеней с целым показателем. Теорема Виета. Разложение квадратного трехчлена на линейные множители.
Алгебраическая дробь. Сокращение дробей. Действия с алгебраическими дробями. Представление дроби в виде суммы дробей с использованием метода неопределенных коэффициентов.
Рациональные выражения и их преобразование. Свойства квадратных корней и их применение в вычислениях.
Уравнения и неравенства. Квадратное уравнение: формула корней квадратного уравнения. Решение рациональных уравнений. Примеры решения уравнений высших степеней; методы замены переменной, разложение на множители.
Уравнения с двумя переменными. Примеры решения нелинейных систем. Примеры решения нелинейных уравнений в целых числах.
Неравенство с одной переменной. Решение неравенств. Линейные неравенства с одной переменной и их системы. Квадратные неравенства. Дробно – рациональные неравенства. Неравенства, содержащие переменную под знаком модуля.
Переход от словесной формулировки соотношений между величинами к алгебраической и обратно. Решение текстовых задач алгебраическим способом.
Числовые функции. Область определения и область значений функции. Чтение графиков функций. Преобразование графиков функций: растяжение, сжатие, параллельный перенос вдоль осей координат.
График функции у = 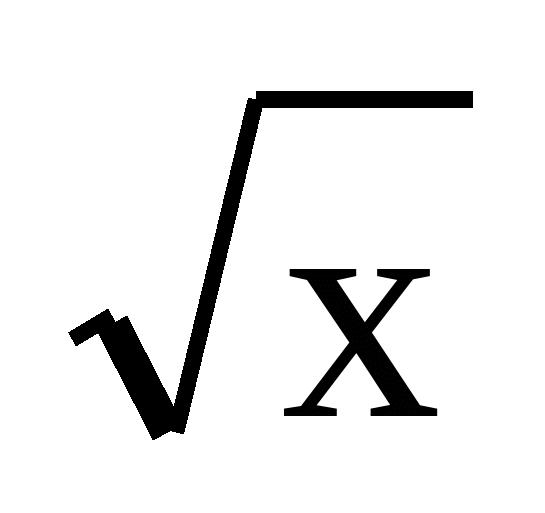 . Дробно – линейная функция и ее график. Использование графиков функций для решения уравнений и систем. . Дробно – линейная функция и ее график. Использование графиков функций для решения уравнений и систем.
Координаты. Числовые промежутки: Интервал, отрезок, луч. Графическая интерпретация уравнений с двумя переменными и их систем.
Элементы логики, комбинаторики, статики и теории вероятностей.
Множества и комбинаторика. Объединение и пересечение множеств. Взаимно однозначное соответствие. Замкнутость множества относительно операции сложения (умножения, деления, вычитания). Число элементов объединения и пересечения двух конечных множеств. Понятие о мощности множеств. Принцип Дирихле.
Статистические данные. Интервальный ряд данных. Относительная частота варианты.
Формы и средства контроля
Основными методами проверки знаний и умений учащихся по математике являются устный опрос и письменные работы. К письменным формам контроля относятся: математические диктанты, самостоятельные и контрольные работы, тесты. Основные виды проверки знаний – текущая и итоговая. Текущая проверка проводится систематически из урока в урок, а итоговая – по завершении темы (раздела), школьного курса. Для проведения контрольных и самостоятельных работ, тестов используется «Алгебра. 8 класс. Дидактические материалы. Методические рекомендации / И.Е. Феоктистов.- М.: Мнемозина, 2011.-173с.».
Календарно-тематическое планирование
-
№
|
Содержание
|
Пункт учебника
|
Тип учебного занятия
|
Примерные сроки
|
Подготовка к ГИА
|
Повторение материала 7-х классов (6 часов)
|
1
|
Повторение. Многочлены, действия с многочленами, формулы сокращенного умножения.
|
|
ПМ
|
02.09
|
2.1.7
|
2
|
Повторение. Разложение на множители: вынесение за скобку, группировка.
|
|
ПМ
|
02.09
|
2.1.8
|
3
|
Повторение. Уравнения, решение уравнений разложением на множители.
|
|
ПМ
|
06.09
|
2.2.5
|
4
|
Повторение. Функции и их графики. Уравнения с двумя переменными и их графики.
|
|
ПМ
|
07.09
|
2.2.4
|
5
|
Повторение. Системы линейных уравнений и методы их решения.
|
|
ПМ
|
07.09
|
2.2.8
|
6
|
Входное тестирование.
|
|
КЗ
|
09.09
|
|
Глава I. Дроби (23 ч.).
|
§ 1. Дроби и их свойства.(5 ч.)
|
7
|
Числовые дроби и дроби, содержащие переменные.
|
П.1
|
ИНМ
|
09.09
|
1.2.1
|
8
|
Числовые дроби и дроби, содержащие переменные.
|
П.1
|
УКПЗ
|
13.09
|
1.2.1
|
9
|
Свойства дробей.
|
П.2
|
ИНМ
|
14.09
|
1.2.2
|
10
|
Свойства дробей.
|
П.2
|
УКПЗ
|
14.09
|
1.2.2
|
11
|
Самостоятельная работа « Дроби и их свойства».
|
|
КЗ
|
16.09
|
1.2.2
|
§2.Сумма и разность дробей. (6 часов)
|
12
|
Сложение и вычитание дробей.
|
П. 3
|
ИНМ
|
16.09
|
1.2.3
|
13
|
Сложение и вычитание дробей.
|
П. 3
|
ЗПЗ
|
20.09
|
1.2.3
|
14
|
Сложение и вычитание дробей.
|
П. 3
|
УКПЗ
|
21.09
|
1.2.4
|
15
|
Представление дроби в виде суммы дробей.
|
П. 4
|
ИНМ
|
21.09
|
1.2.4
|
16
|
Представление дроби в виде суммы дробей.
|
П. 4
|
УКПЗ
|
23.09
|
1.2.5
|
17
|
Самостоятельная работа «Сложение и вычитание дробей».
|
|
КЗ
|
23.09
|
2.1.11
|
§3. Произведение и частное дробей.(12 часов)
|
18
|
Умножение дробей. Возведение дроби в степень.
|
П.5
|
ИНМ
|
27.09
|
1.3.1
|
19
|
Умножение дробей. Возведение дроби в степень.
|
П.5
|
УКПЗ
|
28.09
|
1.3.1
|
20
|
Деление дробей.
|
П.6
|
ИНМ
|
28.09
|
1.3.2
|
21
|
Деление дробей.
|
П.6
|
ЗПЗ
|
30.09
|
1.3.2
|
22
|
Самостоятельная работа «Умножение, возведение в степень и деление дробей».
|
П.6
|
УКПЗ
|
30.09
|
2.1.11
|
23
|
Преобразование рациональных выражений.
|
П.7
|
ИНМ
|
04.10
|
1.3.3.
|
24
|
Преобразование рациональных выражений.
|
П.7
|
ЗПЗ
|
05.10
|
1.3.4
|
25
|
Преобразование рациональных выражений.
|
П.7
|
УКПЗ
|
05.10
|
1.3.4
|
26
|
Самостоятельная работа «Преобразование рациональных выражений».
|
П.7
|
КЗ
|
07.10
|
2.1.12
|
27
|
Решение дополнительных упражнений к главе 1.
|
П. 1-7
|
УОСМ
|
07.10
|
2.1.12
|
28
|
Решение дополнительных упражнений к главе 1.
|
П. 1-7
|
УОСМ
|
11.10
|
2.1.12
|
29
|
Контрольная работа №1 «Дроби».
|
П. 1-7
|
КЗ
|
12.10
|
|
Глава II. Целые числа. Делимость чисел.(19 ч.)
|
§4. Множество натуральных и множество целых чисел. (5ч.)
|
30
|
Пересечение и объединение множеств.
|
П. 8
|
ИНМ
|
12.10
|
1.3.5
|
31
|
Пересечение и объединение множеств.
|
П. 8
|
УКПЗ
|
14.10
|
1.3.6
|
32
|
Взаимно однозначное соответствие.
|
П. 9
|
ИНМ
|
14.10
|
1.6.1
|
33
|
Натуральные числа. Целые числа.
|
П.10
|
ИНМ
|
18.10
|
1.6.2
|
34
|
Самостоятельная работа «Множество натуральных и множество целых чисел».
|
П. 8-10
|
КЗ
|
19.10
|
|
§5. Делимость чисел. (14 ч.)
|
35
|
Свойства делимости.
|
П. 11
|
ИНМ
|
19.10
|
1.6.2
|
36
|
Делимость суммы и произведения.
|
П. 12
|
ИНМ
|
21.10
|
1.6.3.
|
37
|
Делимость суммы и произведения.
|
П. 12
|
УКПЗ
|
21.10
|
1.6.3.
|
38
|
Самостоятельная работа «Свойства делимости, делимость суммы и произведения».
|
П. 11-12
|
КЗ
|
25.10
|
1.6.4.
|
39
|
Деление с остатком.
|
П.13
|
ИНМ
|
26.10
|
1.6.5
|
40
|
Деление с остатком.
|
П.13
|
УКПЗ
|
26.10
|
1.6.6.
|
41
|
Признаки делимости.
|
П.14
|
ИНМ
|
28.10
|
1.6.6.
|
42
|
Признаки делимости.
|
П.14
|
УКПЗ
|
28.10
|
1.6.7.
|
43
|
Простые и составные числа.
|
П.15
|
ИНМ
|
08.11
|
1.5.1
|
44
|
Простые и составные числа.
|
П.15
|
УКПЗ
|
09.11
|
1.5.1
|
45
|
Самостоятельная работа «Признаки делимости».
|
П. 13-15
|
КЗ
|
09.11
|
2.1.1
|
46
|
Решение дополнительных упражнений к главе 2.
|
П. 11-15
|
УОСМ
|
11.11
|
2.1.1
|
47
|
Решение дополнительных упражнений к главе 2.
|
П. 11-15
|
УОСМ
|
11.11
|
2.1.2
|
48
|
Контрольная работа №2 «Делимость чисел».
|
П. 11-15
|
КЗ
|
15.11
|
|
Глава III. Действительные числа. Квадратный корень(29ч.)
|
§6. Множество рациональных и действительных чисел (10 ч.)
|
49
|
Рациональные числа.
|
П.16
|
ИНМ
|
16.11
|
2.1.2
|
50
|
Рациональные числа.
|
П.16
|
УКПЗ
|
16.11
|
2.1.3
|
51
|
Действительные числа.
|
П.17
|
ИНМ
|
18.11
|
2.1.4
|
52
|
Действительные числа. Тест.
|
П.17
|
УКПЗ
|
18.11
|
2.1.6
|
53
|
Числовые промежутки.
|
П.18
|
ИНМ
|
22.11
|
2.1.7
|
54
|
Числовые промежутки.
|
П.18
|
УКПЗ
|
23.11
|
|
55
|
Интервальный ряд данных.
|
П.19
|
ИНМ
|
23.11
|
2.1.8
|
56
|
Абсолютная и относительная погрешность.
|
П.20
|
ИНМ
|
25.11
|
2.1.8
|
57
|
Абсолютная и относительная погрешность.
|
П.20
|
ИНМ
|
25.11
|
2.1.10
|
58
|
Самостоятельная работа. «Приближённые вычисления».
|
П. 16-20
|
КЗ
|
29.11
|
|
§7.Арифметический квадратный корень(6 ч.)
|
59
|
Арифметический квадратный корень.
|
П.21
|
ИНМ
|
30.11
|
2.1.11
|
60
|
Арифметический квадратный корень. Тест.
|
П.21
|
УКПЗ
|
30.11
|
2.1.12
|
61
|
Вычисление и оценка значений квадратных корней.
|
П.22
|
ИНМ
|
02.12
|
2.2.1
|
62
|
Вычисление и оценка значений квадратных корней.
|
П.22
|
УКПЗ
|
02.12
|
2.2.2
|
63
|
Функция 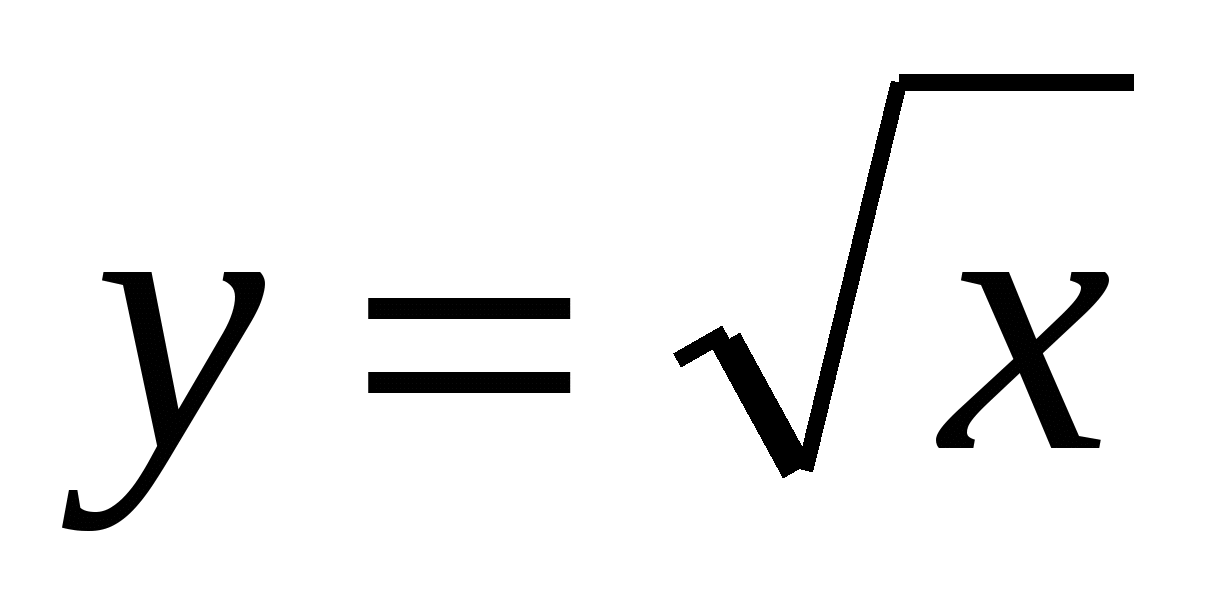 и её график. и её график.
|
П.23
|
ИНМ
|
06.12
|
2.2.7
|
64
|
Самостоятельная работа. «Арифметический квадратный корень».
|
П 39-.41
|
КЗ
|
07.12
|
|
§8. Свойства арифметического квадратного корня (13 ч.)
|
65
|
Квадратный корень из произведения, дроби и степени.
|
П.24
|
ИНМ
|
07.12
|
1.4.1
|
66
|
Квадратный корень из произведения, дроби и степени.
|
П.24
|
зпз
|
09.12
|
1.4.1
|
67
|
Квадратный корень из произведения, дроби и степени. Тест.
|
П.24
|
УКПЗ
|
09.12
|
1.4.3
|
68
|
Преобразование выражений, содержащих квадратные корни.
|
П.25
|
ИНМ
|
13.12
|
1.4.3
|
69
|
Преобразование выражений, содержащих квадратные корни.
|
П.25
|
ЗПЗ
|
14.12
|
1.4.4
|
70
|
Преобразование выражений, содержащих квадратные корни.
|
П.25
|
УКПЗ
|
14.12
|
1.4.4
|
71
|
Самостоятельная работа «Свойства арифметического квадратного корня».
|
П. 24-25
|
КЗ
|
16.12
|
|
72
|
Преобразование двойных радикалов.
|
П.26
|
ИНМ
|
16.12
|
1.4.5
|
73
|
Преобразование двойных радикалов.
|
П.26
|
УКПЗ
|
20.12
|
1.4.5
|
74
|
Самостоятельная работа «Преобразование двойных радикалов».
|
П. 26
|
КЗ
|
21.12
|
| |
|
|
 Скачать 0.51 Mb.
Скачать 0.51 Mb.