Активизация самостоятельной деятельности на уроках математики как условие для развития личности школьника
 Скачать 245.48 Kb. Скачать 245.48 Kb.
|
| Активизация самостоятельной деятельности на уроках математики как условие для развития личности школьника Автор опыта: Стороженко Эммы Петровны учитель математики МОУ Божковской ООШ Алексеевского района Белгородской области Содержание: 1. Информация об опыте………………………………........ ………………………3 2. Технология опыта……………………………………...... ………………………. 9 3. Результативность опыта…………………………………………………………16 4. Библиографический список……………………………………………………...17 5. Приложения к опыту……………………………………………………………..18 Раздел I. Информация об опыте Условия возникновения и становления опыта «Дорогу осилит идущий, а математику – мыслящий» Д. Пойа Школа, в которой я работаю, МОУ Божковская ООШ, маленькая. В ней обучается 33 человека, количество учащихся в классе - 3-5 человек. В школе обучаются представители разных национальностей. В школе имеется компьютерный класс, копировальная техника, сканеры, медиатека, есть выход в интернет. Кабинеты оснащены компьютерами, мультимедийными проекторами. Это позволяет проводить уроки с использованием информационно-коммуникативных технологий. Я работаю учителем математики 26 лет. У многих школьников отмечается равнодушие к знаниям, нежелание учиться, низкий уровень развития познавательных интересов. Поэтому я считаю, что главная задача педагога в этих условиях заключается в поиске более эффективных форм, моделей, способов и условий обучения. Таким образом, на первый план выходит проблема активизации деятельности учащихся в процессе обучения. Проблема активности личности в обучении – это ведущий фактор достижения целей обучения, общего развития личности, её профессиональной подготовки. Н.А.Половникова называет три уровня развития познавательной самостоятельности учащихся, положив в основу степень владения методами самостоятельной познавательной деятельности. На первом уровне – копирующая самостоятельность – школьник овладевает образцами всех типичных для его класса форм познавательной деятельности по предмету. В основном, здесь подразумевается овладение алгоритмическими действиями (по аналогии, по заранее представленному плану и т.п.), ведущими всех учащихся при одинаковых исходных данных к определенному, одинаковому результату. Второй уровень – воспроизводяще-выборочная (репродуцирующая) самостоятельность – характеризуется самостоятельным воспроизведением основных методов, соответствующих ступени обучения школьника, способностью к выбору и использованию нужного метода. Третий уровень познавательной самостоятельности – творческая самостоятельность школьников – состоит прежде всего в уяснении конструктивного подхода к творчеству, в создании новых методов познавательной самостоятельности на основе уже усвоенных. Началом работы по теме стало проведение диагностики пятиклассников по определению уровня самостоятельности.
Психофизиологические особенности учащихся, разные уровни их умственных способностей, закономерно требуют для обеспечения эффективного учебного процесса каждого ребенка или группы детей неодинаковых условий обучения. Поэтому встал вопрос, как организовать обучение, чтобы оно осуществлялось на оптимальном уровне трудности и способствовало развитию всех учащихся, в том числе и самых слабых, и самых сильных. Важность этой проблемы побудила начать работу по изучению теоретических и практических аспектов организации самостоятельной работы, как залога успешного саморазвития личности школьника. Актуальность опыта Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не памятью. Л.Н.Толстой Развитие активности, самостоятельности, инициативы, творческого отношения к делу – это требования самой жизни, определяющие во многом то направление, в котором следует совершенствовать учебно-воспитательный процесс. Процессы развития общества неразрывно связаны с активизацией человеческого фактора, развитием творческой активности людей во всех сферах общественной и производственной деятельности. Поэтому развитие общеобразовательной школы предполагает ориентацию образования не только на усвоение знаний, умений и навыков, но и на развитие личности, её познавательных способностей. Без развития познавательной активности, умения самостоятельно пополнять свои знания, нельзя решить задачи по формированию нового человека. Общеизвестно, что учащиеся прочно усваивают только то, что прошло через их индивидуальное усилие. Проблема самостоятельности учащихся при обучении не является новой. Этому вопросу отводили исключительную роль ученые всех времен. Особенно четкие концепции о роли самостоятельности в приобретении знаний имеются в трудах К.Д.Ушинского, Н.Г.Чернышевского, Д.И.Писарева и др. Эта проблема является актуальной и сейчас. Математика объективно является одной из самых сложных школьных дисциплин и вызывает субъективные трудности у многих учащихся. В то же время имеются дети с явно выраженными способностями к этому предмету. Поэтому надо строить работу так, чтобы на уроках было интересно каждому учащемуся. Математика относится к числу школьных предметов с наиболее ярко выраженными межпредметными связями. Развитие логического мышления, которое осуществляется на уроках, оказывает серьёзное влияние на изучение многих предметов в школьном расписании. Обучение математике способствует умственному развитию, в процессе которого у учащихся вырабатываются умения обобщать и конкретизировать, систематизировать и классифицировать, проводить анализ. Формируются также личные качества: точность, сосредоточенность, внимание, настойчивость, ясность словесного выражения мысли. А как понять предмет, если он кажется ученику скучным, уроки однообразными? У определенной части учащихся наблюдается довольно низкий уровень интереса к учению, негативное отношение к знаниям. Из-за низкого уровня мыслительной деятельности учащиеся размышляют шаблонно, стремятся действовать знакомым способом. Проявление интереса к предмету можно добиться путём применения новых современных или как их сейчас называют инновационных технологий в обучении. Важное место в комплексе задач обучения математике занимает проблема активизации мыслительной деятельности обучаемых. Современная концепция обучения сегодня состоит в том, что учащийся должен учиться сам, а учитель – осуществлять мотивационное управление его учением, т.е. мотивировать, организовывать, координировать, консультировать его деятельность. Вопросы активизации учения учащихся относятся к числу наиболее актуальных проблем современной педагогической науки и практики. Реализация принципа активности в обучении имеет определенное значение, т.к. обучение и развитие носят деятельностный характер, и от качества учения как деятельности зависит результат обучения, развития и воспитания учащихся. Ключевой проблемой в решении задачи повышения эффективности и качества учебного процесса является активизация учения учащихся. Ее особая значимость состоит в том, что учение, являясь отражательно преобразующей деятельностью, направлено не только на восприятие учебного материала, но и на формирование отношения учащихся к самой познавательной деятельности. Деятельность протекает более эффективно и дает более качественные результаты, если у учащихся имеются сильные, яркие и глубокие мотивы, вызывающие желание действовать активно, преодолевать неизбежные затруднения, настойчиво продвигаясь к намеченной цели. Учебная деятельность идет более успешно, если у учеников сформировано положительное отношение к учению, есть познавательный интерес и потребность в познавательной деятельности, а также, если у них воспитаны чувства ответственности и обязательности. Очень важно, чтобы вступая в сложный взрослый мир ученик имел такие качества личности, как умение анализировать, решать проблемы, умение самостоятельно принимать решения, применять знания в своей практике, творить. И моя задача в том, чтобы развивать у учащихся познавательный интерес, творческое отношение к делу, стремление к самостоятельному добыванию знаний и умений, применения их в своей практической деятельности. Ведущая педагогическая идея опыта Ведущая педагогическая идея опыта – заключается в развитии познавательной активности учащихся, при изучении математики на основе самостоятельной работы. Не учитель теперь призван обучать математике школьников, а сами ученики в созданных учителем обучающих ситуациях, самостоятельно или в сотрудничестве друг с другом (или с учителем)овладевают системой математических знаний, умений и навыков. Длительность работы над опытом Учебно-воспитательный процесс, в классах с 2011 года по 2014 год, стал процессом целенаправленного, планомерного, педагогически организованного развития познавательной активности учащихся, осуществляемого на основе включения в практику инновационных форм организации учебно-воспитательного процесса, новых средств обучения, информационных методов обучения, стимулирующих активное добывание знаний и овладение учащимися способами познавательной деятельности. Диапазон опыта Диапазон данного опыта работы представлен системой работы учителя при организации уроков математики. Теоретическая база опыта В своей работе опираюсь на учение об активности, основы которого заложены Л.С. Выготским, согласно которому активность - это практическая предметно-чувственная деятельность, направленная не только на преобразование окружающего мира, но и на преобразование самой личности - важнейшее условие и фактор ее психического развития. В основу разработки данной проблемы положено понимание сущности познавательной активности учащихся Т. И. Шамовой, которая рассматривает познавательную активность «как качество деятельности личности, которое проявляется в отношении ученика к содержанию и процессу деятельности, в стремлении его к эффективному овладению знаниями и способами деятельности за оптимальное время, в мобилизации нравственно-волевых усилий на достижение учебно-познавательных целей». Одним из инструментов развития мышления, ведущего к формированию творческой деятельности, является самостоятельная работа. Самостоятельная работа учащихся - это форма организации их учебной деятельности, осуществляемая под прямым или косвенным руководством преподавателя, в ходе которой учащиеся преимущественно или полностью самостоятельно выполняют различного вида здания с целью развития знаний, умений, навыков и личных качеств. Самостоятельная работа, на мой взгляд, наиболее полно определяется А.И. Зимней. По её определению самостоятельная работа представляется как целенаправленная, внутренне мотивированная структурированная самим объектом в совокупности выполняемых действий и корригируемая им по процессу и результату деятельности. Её выполнение требует достаточно высокого уровня самосознания, рефлективности, самодисциплины, личной ответственности, доставляет ученику удовлетворение как процесс самосовершенствования и самопознания. Во-первых, в данном определении принимаются во внимание психологические детерминанты самостоятельной работы: саморегуляция, самоактивация, самоорганизация, самоконтроль и т.д. Во-вторых, А.И. Зимняя подчёркивает, что самостоятельная работа школьника есть следствие правильно организованной его учебной деятельности на уроке, что мотивирует самостоятельное её расширение, углубление и продолжение в свободное время. Для учителя это означает чёткое осознание не только своего плана учебных действий, но и осознанное его формирование у школьников как некоторой схемы освоения учебного предмета в ходе решения новых учебных задач. Но в целом это параллельно существующая занятость школьника по выбранной им из готовых программ или им самим выработанной программе усвоения какого-либо материала. В-третьих, самостоятельная работа рассматривается как высший тип учебной деятельности, требующий от учащегося достаточно высокого уровня самосознания, рефлексивности, самодисциплины, ответственности, и доставляющий ученику удовлетворение, как процесс самосовершенствования и самосознания. Разделяя точку зрения П. Н. Груздева, Ш. Н. Ганелина, Р. Г. Ламберга, автор опыта предпринял попытку проанализировать влияние самостоятельной работы учащихся на развитие познавательной активности и пришел к выводу, что эффект от самостоятельной работы учащегося можно получить только тогда, когда она организуется и реализуется в учебно-воспитательном процессе в качестве целостной системы, пронизывающей все этапы обучения учащегося в школе. При проектировании системы развития познавательной активности учащихся на основе самостоятельной работы автор опыта использует идеи профессора Т.И. Шамовой, профессора Т.М. Давыденко, Ю.А. Конаржевского, И.С.Якиманской. Согласно их идеям условиями развития познавательной активности являются: максимальная опора на активную мыслительную деятельность учащихся; ведение учебного процесса на оптимальном уровне развития учащихся; эмоциональная атмосфера обучения, положительный эмоциональный тонус учебного процесса. Эффективность учебного процесса познания определяется качеством преподавания и самостоятельной познавательной деятельностью учеников. И.Я.Лернер выделяет четыре уровня познавательной самостоятельности на основе умения познавать в процессе целенаправленного творческого поиска, описывая их следующим образом: 1-й уровень. Учащиеся самостоятельно и доказательно строят один или несколько непосредственных выводов из одного исходного. 2-й уровень. Умение доказательно прийти к нескольким параллельным и изолированным друг от друга непосредственным выводам на основе нескольких различных данных. 3-й уровень. Умение сделать доказательно один или несколько опосредованных выводов из одного или нескольких данных условия, при этом все выводы должны быть изолированы друг от друга. 4-й уровень. Умение делать опосредованные выводы на основе выявления связи между различными данными условия. Новизна опыта Новизна опыта моей работы заключается в комбинировании элементов известных методик и технологий, способствующих развитию самостоятельности на уроках математики. Новизна опыта проявляется в отборе разноуровневых задач по математике, широком использовании методов работы с любыми источниками информации (учебника, интернета, справочной литературой), оригинальной компоновке учебного материала. Раздел II Технология опыта Целью педагогической деятельности является обеспечение положительной динамики творческой самореализации учащихся на уроках математики, раскрытие индивидуальности ребёнка, что создаёт благоприятные условия для формирования учебно-интеллектуальных умений и навыков, для развития самостоятельной познавательной активности, профессиональной направленности личности. Для достижения поставленной цели сформулирую следующие задачи: - введение в педагогическую практику такой организации образовательного процесса, которая предполагает создание учителем условий для позитивного изменения уровня познавательной активности учащихся и предоставляет возможность для самореализации каждого ученика в учебной деятельности; -включение в учебный процесс групповых и индивидуальных форм его организации, стимулирующих активное овладение учащимися способами познавательной деятельности; -использование методов и приемов, педагогических техник и средств, способствующих самостоятельности учащихся в познавательной деятельности. Организация учебно-воспитательного процесса Организация образовательного процесса строится на основе базисного учебного плана, индивидуального учебного плана школы, разработанного с учетом соблюдения норм максимально допустимой нагрузки обучающихся. Учебные планы и программы утверждаются на заседаниях МО и решением педагогического совета школы. Организация учебно–воспитательного процесса основана на использовании следующих этапов:
Изучение нового учебного материала. Сопровождается осуществлением мер по широкому использованию в учебном процессе коммуникативно– деятельностного, индивидуально-личностного и проблемного подходов. Закрепление и комплексное применение знаний и способов действий. Использование практикумов, учебных проектов и других видов самостоятельной работы учащихся по применению полученных знаний. Применяются групповые и индивидуальные формы работы, постепенно увеличивается уровень сложности решаемых задач, используются творческие задания для повышения креативности мышления. Задания подбираются так, чтобы ученики могли справиться с предложенной работой (самостоятельно или с помощью учителя), чтобы каждый школьник в ходе учебных занятий оказался в ситуации успеха в соответствии с уровнем его способностей, имея возможность получить необходимую своевременную помощь. Учебный труд, как и всякий другой, интересен тогда, когда он разнообразен. Однообразная информация и однообразные способы действия очень быстро вызывают скуку. Работа учителя по активизации познавательной деятельности учащихся наиболее эффективна, а качество знаний учащихся выше, если при проведении уроков используются приемы и средства, активизирующие их познавательный интерес. В урок включаются:
Для саморазвития школьников разного возраста целесообразно использование специфических форм организации работы:
Например: «Ромашка» 
Например: «Пирамида» 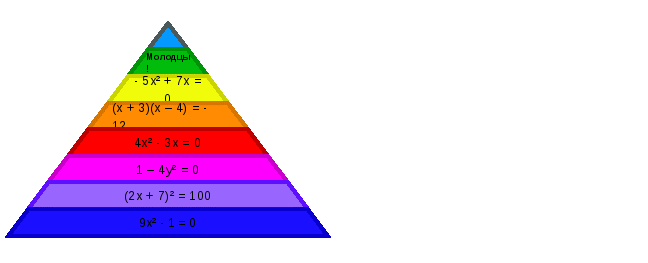
Самостоятельная работа важнейшее условие саморегуляции личности, ее творческих возможностей. Самостоятельная работа ученика - главный путь воспитания самостоятельности. Но самостоятельная работа, привлекая современных школьников, вызывает в тоже время у многих серьезные затруднения. Она требует эмоционального и умственного напряжения, порождает массу неожиданных вопросов и ошибок, сомнения и переживания. В своей работе я хочу осветить вопросы о правильности организации самостоятельной работы, так как я считаю, что самостоятельная работа служит эффективным средством формирования личности, побуждает умственную самостоятельность у детей. Она дисциплинирует мысль, рождает у школьников веру в себя, в свои силы и возможности. В процессе обучения математике задача учителя состоит не только в том, чтобы обеспечивать прочные знания, предусмотренные программой, но и в том, чтобы развивать самостоятельность и активность мышления учащихся. В соответствии с поставленными целями и задачами педагогической деятельности в рамках представляемого опыта используются разнообразные формы, методы и средства учебно-воспитательной работы. В теории и практике обучения наиболее распространены следующие подходы к классификации самостоятельных работ: по дидактическим целям (обучающие, контролирующие, развивающие); по уровню самостоятельности учащихся (по образцу, реконструктивно-вариативные, частично-поисковые (эвристические), исследовательские (творческие)); по степени индивидуализации (классные, групповые и индивидуальные); по источнику и методу приобретения знаний (работа с книгой, решение и составление задач, лабораторные и практические работы, подготовка докладов, рефератов и т.д.) по форме выполнения (устные и письменные самостоятельные работы); по месту выполнения (классные и домашние). Рассмотрим некоторые виды самостоятельных работ и их сочетание более подробно. Классификация по степени индивидуализации включает общеклассные, групповые и индивидуальные самостоятельные работы. Их проводят, в той или иной мере учитывая индивидуальные особенности каждого ученика, в условиях органического соединения индивидуальной и коллективной деятельности учащихся. Самостоятельные работы по дидактическому назначению можно разделить на обучающие, контролирующие и развивающие. Обучающие работы предназначены для организации самостоятельной деятельности учащихся, ориентированной на усвоение знаний и выработку умений применять их. Они часто носят индивидуальный характер и предназначены для ребят, по тем или иным причинам, не усвоившим материал вместе с остальной частью класса. Обучающие самостоятельные работы в свою очередь подразделяют на работы по формированию знаний и работы по формированию умений. Во всех случаях надо стремиться проводить обучающие работы в непринужденной, деловой обстановке, чтобы ребята не боялись задавать любые вопросы, были бы уверены, что за ошибки их не накажут, а там, где требуется, помогут, покажут, повторно разъяснят. (Приложение 3) Развивающие самостоятельные работы даются либо индивидуально каждому ученику, либо всему классу сразу с целью привлечения внимания к нестандартным заданиям, которые способствуют развитию логического мышления. Такие задания полезно давать ученикам в качестве домашней работы. На уроках развивающим задачам обычно отводят немного времени и предлагают ученикам в конце урока, если остается время после изучения запланированного материала, либо в начале, в качестве разминки. Если систематически уделять 5-10 минут урока таким задачам результаты не заставят себя ждать. Например: 1. Найти сходство (общие признаки, свойства, характеристики) у разных геометрических объектов (у ромба и прямоугольника; треугольника и трапеции; окружности и сферы; смежных углов и вертикальных углов и т. д.). 2. а) Перечислить как можно больше геометрических объектов с данным свойством (имеет прямой угол; содержит 4 отрезка; диагонали точкой пересечения делятся пополам; можно вписать окружность). б) Перечислить как можно больше предметов, обладающих несколькими заданными свойствами (имеет прямой угол и острый; имеет два равных угла). Развивающими являются самостоятельные работы с переадресацией цели. Например, задания с кодами. На урок задаются примеры, решая которые ученик получает ответ. Все ответы и посторонние значения заносятся в таблицу, где напротив значения указана буква или слог. Из полученных ответов-букв (слогов) складываются слова или предложения. Контролирующие самостоятельные работы призваны проверить степень усвоения материала учениками для своевременной коррекции знаний и накопления оценок. Нередко со всеми учащимися класса проводятся двух и более вариантные самостоятельные работы, идентичные по содержанию. Ныне же все большее применение получают дифференцированные самостоятельные работы, соответствующие разному уровню подготовленности учащихся одного и того же класса. Обычно в практике обучения используются до восьми вариантов разноуровневых заданий. В практике для развития самостоятельности мышления, учитель использует самостоятельные и контрольные работы не менее чем в четырех вариантах. В зависимости от степени сложности темы, работы дифференцируются по уровням сложности. Обычно применяет 2 уровня сложности, реже три. К первому, более легкому уровню, часто прилагается справочный материал, опорные формулы. (Приложение 4) Одним из видов самостоятельных ра6от, являются работы в которых дифференцирована лишь помощь, оказываемая учащимся. Основу такой работы составляют одни и те же задания. Варьируется только система указаний для групп учащихся с различным уровнем подготовленности. Такие работы Г.И. Саранцев называет многовариативными. Степень подсказок может быть разной, вплоть до заполнения пропусков необходимыми вычислениями. (Приложение 5) При выполнении самостоятельных работ по образцу учащиеся не выходят за рамки воспроизводящей деятельности, которая направлена на овладение основными знаниями, умениями, способами работы. Предлагаемые при этом задания выполняются по образцам и алгоритмам, показанным учителем или подробно описанным в учебнике. Они играют важную роль при первичном закреплении изученного, ибо способствуют созданию условий для перехода учащихся к выполнению заданий, требующих более высокого уровня самостоятельности. Поэтому учитель должен уметь отбирать, вовремя предъявлять и требовать от учащихся их точного воспроизведения. Самостоятельные работы реконструктивно-вариативного вида обычно содержат в себе задачи, по условиям которых учащимся приходится анализировать новые для них ситуации, переформулировать их, выбирать из известных способов наиболее рациональные. Они отличаются от работ по образцу тем, что при их выполнении необходимо преобразовать исходные данные, т.е. проявить более высокий уровень самостоятельности. (Приложение 6) Еще более высокий уровень самостоятельности учащиеся проявляют при выполнении частично-поисковых (эвристических) работ, требующих переноса знаний и умений в необычные, нестандартные ситуации. Высшая степень самостоятельности учащихся проявляется при выполнении исследовательских (творческих) самостоятельных работ. Здесь, пользуясь накопленными знаниями и умениями, выдвигая и проверяя собственные гипотезы и суждения, они учатся открывать для себя новые сведения об изучаемых объектах. Такие задачи обладают наибольшим развивающим потенциалом. Полезно сначала задавать подобные самостоятельные работы на дом, чтобы ребенок мог попробовать решить задачу без помощи учителя, вникнуть в суть, предложить свой способ решения, а уже затем обсудить решение всем коллективом. Обычно эвристические задачи используются при проведении олимпиад, турниров, конкурсов. Самостоятельные работы разных типов и видов с большим или малым количеством вариантов призваны обеспечить индивидуализацию обучения, его гуманизацию. Они направлены в первую очередь на развитие познавательной самостоятельности ребенка, которая очень необходима для жизни в современном информационном обществе. Совершенствование методики преподавания и методов обучения неразрывно связано с вопросами развития самостоятельности у учащихся. Поэтому использую различные приемы работы с учеником. На занятиях ориентируюсь на всех учащихся в целом и на каждого в отдельности, имея в виду общие знания. Считаю, что такой подход побуждает к работе слабого ученика и стимулирует сильного. Для этого выбираю разные методы работы: устный; словесно-графический; наглядный; практический. Каждый из них реализуется в системе приемов, таких как: фронтальный опрос, устные контрольные работы, построение графиков, диаграмм, фигур на плоскости и в пространстве, работа с ними, с перфокартами, моделями по алгоритму, практические и лабораторные, работа над проектами, сказками, рефератами. Использую дифференцированные средства обучения: таблицы, учебник, схемы, модели фигур и плоскостей, проекты, описание работ, чертежные и измерительные приборы, карточки для устной и письменной работы, дополнительную и справочную литературу. Наша жизнь не стоит на месте. С улучшением материальной базы школ применение компьютеров, информационных ресурсов на уроках даёт учителю новые возможности реализации себя и своих задумок. Применение на уроках медиалекций, игр, моделей, видеофрагментов, графиков, тренажёров переводит образование на более высокую и качественную ступень. Воспитывать интерес к математике и развивать математические способности, а тем более, раскрывать перед учащимися содержание и красоту математики можно только на основе хорошего математического содержания соответствующих мероприятий. Олимпиады, КВН, математические вечера, выпуск математических газет, участие в неделе математики, все это также способствует развитию познавательной активности учащихся, так как для подготовки к этим мероприятиям необходимо самостоятельно ответить на поставленные вопросы, подобрать материал, задуматься над той или иной проблемой. Из всего выше изложенного можно сделать следующий вывод. Самостоятельная работа оказывает значительное влияние на глубину и прочность знаний учащихся по предмету, на развитие их познавательных способностей, на темп усвоения нового материала. При тщательно продуманной методике проведения самостоятельных работ ускоряются темпы формирования у детей умений и навыков практического характера, а это в свою очередь оказывает положительное влияние на формирование познавательных умений и навыков. С течением времени при систематической организации самостоятельной работы на уроках и сочетании её с различными видами домашней работы по математики у учащихся вырабатываются устойчивые навыки самостоятельной работы. В результате для выполнения примерно одинаковых по объёму и степени трудности работ учащиеся затрачивают значительно меньше времени по сравнению с учащимися таких классов, в которых самостоятельная работа совершенно не организуется или проводится нерегулярно. Это позволяет постепенно наращивать темпы изучения программного материала, увеличить время на выполнение заданий различного типа, выполнение исследовательских работ и других видов работ творческого характера. Раздел III Результативность опыта Результаты развития познавательной самостоятельности учащихся по методике Н.А. Половниковой.
Таким образом, результативность деятельности по организации самостоятельной работы на уроках математики имеет положительную динамику от уровня копирующей самостоятельности к уровню творческой самореализации в учебно-познавательной деятельности. Умение проводить работу с различными источниками информации по поиску рационального метода решения, проводить самостоятельно анализ нескольких источников информации по поиску общего вывода, доказательства, умение отобрать наиболее рациональный метод решения задачи, является основой творческого саморазвития личности школьника. Критерием оптимальности методов обучения и возбуждения интереса учащихся к учебной деятельности, к научным исследованиям является эффективность обучения, выражающаяся в высоком уровне усвоения знаний, умений и навыков, интеллектуального развития учащихся (качество знаний по результатам ГИА в 9 классе по математике - 60%)). Библиографический список:
Приложения 1.Приложение1-Тесты изучение индивидуальных особенностей математического мышления школьников. 2. Приложение 2- Презентация «Математика в профессии швея» 3. Приложение 3- Обучающие самостоятельные работы. 4. Приложение 4- Контрольные работы не менее чем в четырех вариантах. 5. Приложение 5- Многовариативные самостоятельные работы. 6. Приложение 6 - Разработка интегрированного урока математика + история. Тема урока: Системность и развитие творческих способностей учащихся через математические задачи с элементами краеведения. |