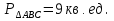|
Урока по геометрии в 8 классе
Урок геометрии в 8 классе по теме «Уравнения окружности и прямой»
Урок рассчитан на 45 минут и направлен на закрепление знаний, умений и навыков, приобретенных при изучении тем «Уравнение прямой» и «Уравнение окружности»; на то, чтобы учить детей на основании теоретических знаний с помощью логических рассуждений находить верный путь решения задач. Урок поддержан авторской мультимедийной презентацией.
Цели урока:
дидактические: отработка ЗУН, приобретенных при изучении данной темы;
развивающие: развитие логического мышления, воображения, творческих способностей;
воспитательные: воспитывать аккуратность записей, культуру речи, самостоятельность.
Тип урока: закрепление ЗУН.
Оборудование: компьютер, мультимедийная приставка.
Время урока: 45 минут
Ход урока.
Организационный момент.
|
2 минуты
|
2. Устная работа (актуализация знаний)
Рисунок 2
№1. Составьте уравнение окружностей, изображенных на рисунках:
Рисунок 1
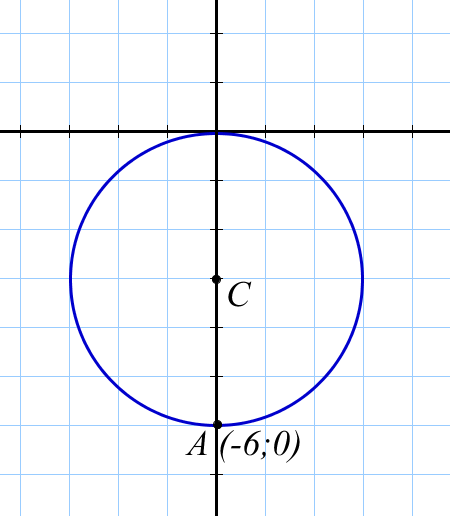
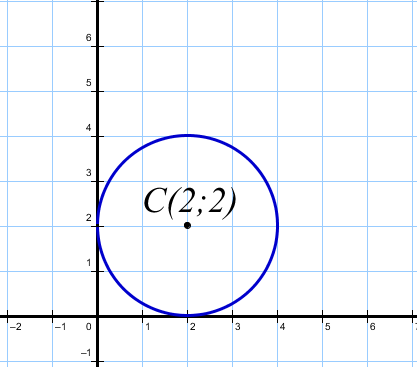
|
8-10 минут
Презентация:
слайды 2-4
Ответ:
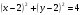
Ответ:
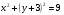
|
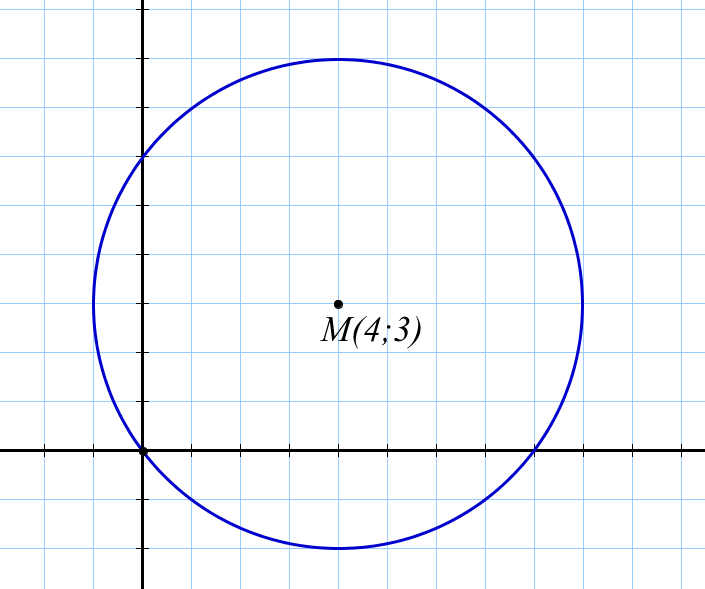
№2. Определите координаты центра и диаметр окружности, заданной уравнением:
а) 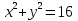 ; ;
б) 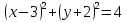 ; ;
в) 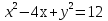 . .
№3. Определите взаимное расположение окружностей 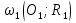 и и 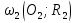 , если , если 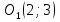 , , 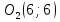 и: и:
а) 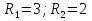 ; ;
б) 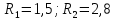 ; ;
в) 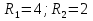 . .
№4. Составьте уравнения прямых, изображенных на рисунках:
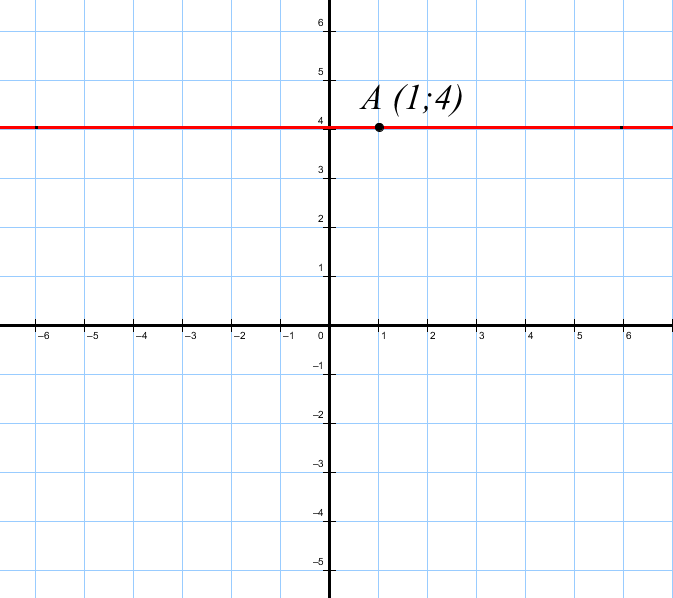
Рисунок 3
Рисунок 4
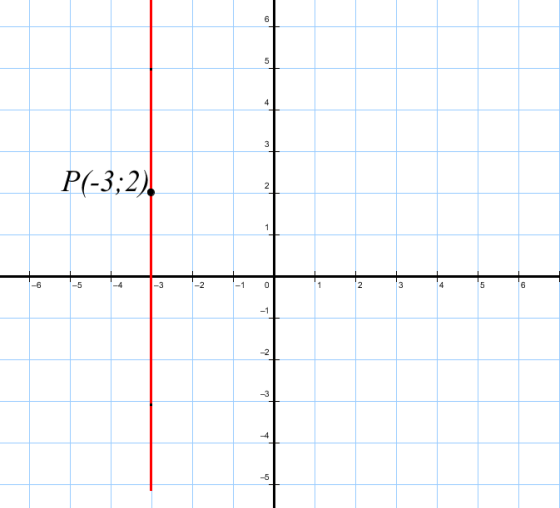
Рисунок 6
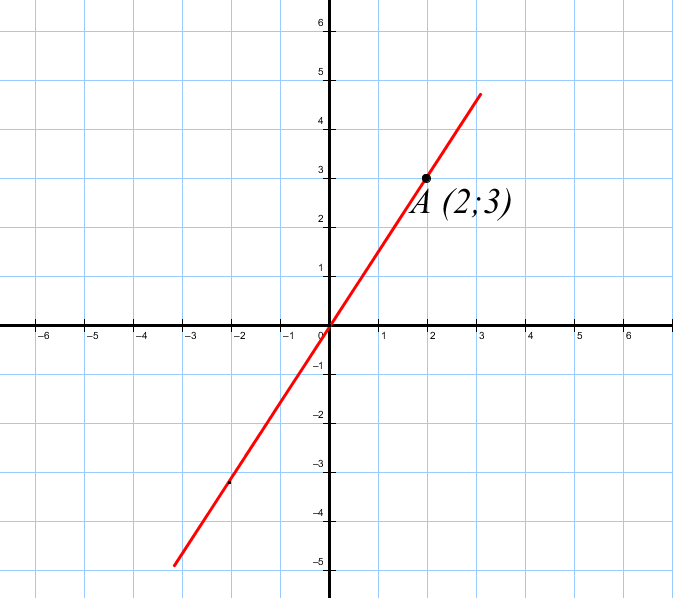
Рисунок 5
№5. Найдите несоответствие геометрической иллюстрации данным задачи:
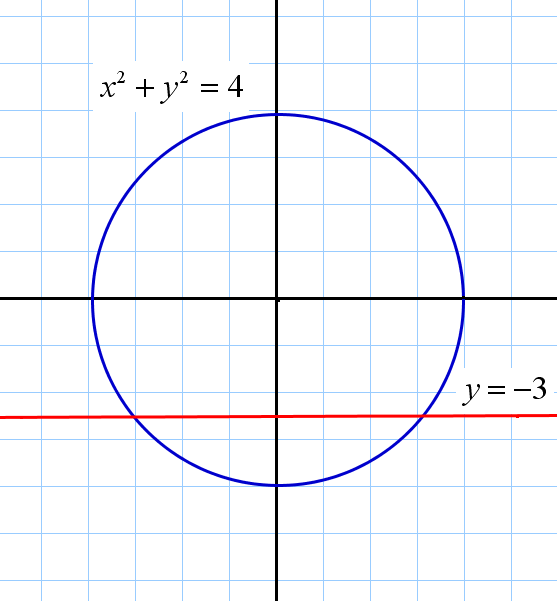
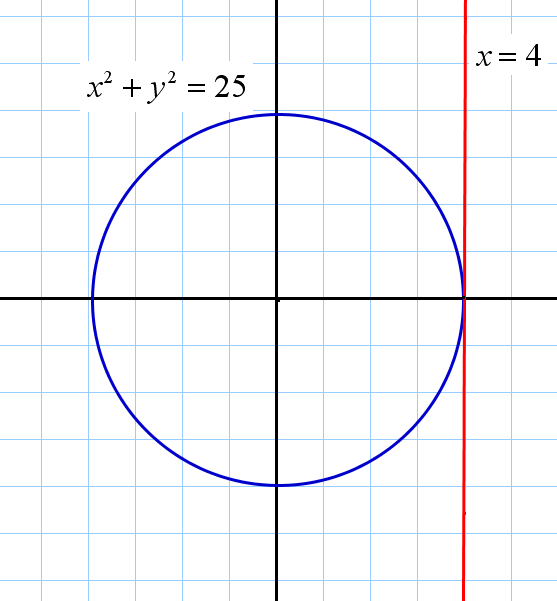
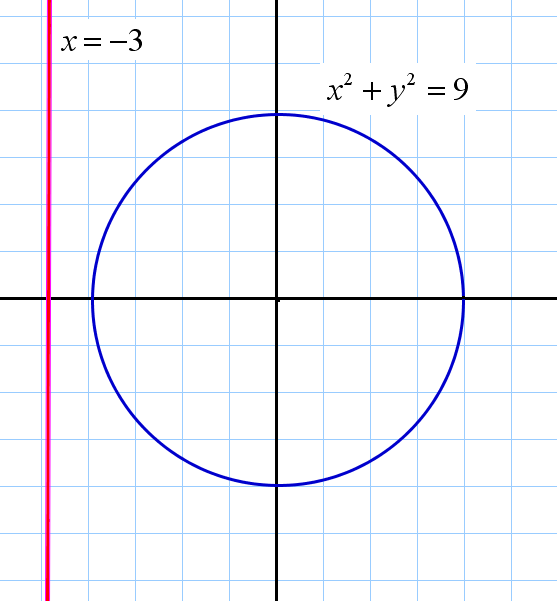
|
Ответ:
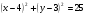
слайд 5
Ответы:
а) 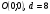 ; ;
б) 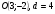 ; ;
в) 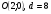 . .
слайд 6
Ответы:
а) касаются внешним образом;
б) не имеют общих точек;
в) пересекаются.
слайды 7-9
Ответ:
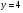 ; ;
Ответ:
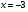 ; ;
Ответ:
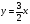 ; ;
слайды 10-12
Ответ:
прямая и окружность не должны иметь общих точек.
Ответ:
прямая и окружность должны пересекаться.
Ответ:
прямая и окружность должны касаться.
|
3. Решение задач.
№1. Используя геометрические соображения, составьте уравнение окружности, проходящей через началоо координат и точки (6;0) и (0;8).
Решение.
1) Так как точки A, O и B принадлежат окружности, то они равноудалены от центра этой окружности.
2) Учитывая, что точки, лежащие на серединном перпендикуляре к отрезку, равноудалены от концов этого отрезка, проведем две прямые l и m, такие что: 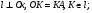 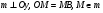 . .
3) 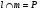 , следовательно точка , следовательно точка 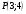 - центр окружности. - центр окружности.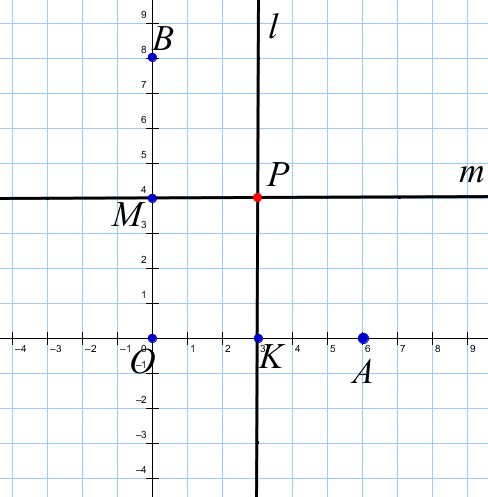
4) Найдем радиус окружности: 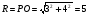 . .
5) Составим уравнение окружности с центром в точке 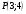 и радиусом и радиусом 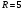 : : 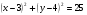
Ответ: 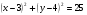 . .
Дополнительое устное задание: составьте уравнение касательной к этой окружности, если известно, что она параллельна оси Ox.
№2. Докажите, что линия, заданная уравнением 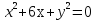 , является окружностью. Является ли отрезок AB, где , является окружностью. Является ли отрезок AB, где 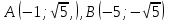 , диаметром этой окружности? , диаметром этой окружности?
Решение.
Преобразуем левую часть уравнения
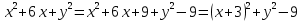 . Тогда исходное уравнение примет вид . Тогда исходное уравнение примет вид 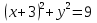 , а это – уравнение окружности с центром в точке , а это – уравнение окружности с центром в точке 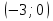 и радиусом равным 3. и радиусом равным 3.
Вычислим координаты середины отрезка AB:
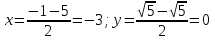 , т.е. координаты середины отрезка AB совпадают с координатами центра заданной окружности. , т.е. координаты середины отрезка AB совпадают с координатами центра заданной окружности.
Докажем, что точка A, например, принадлежит окружности.
Подставим координаты точки A в уравнение окружности, получим:
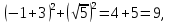
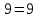 - верное числовое равенство, значит точка A принадлежит заданной окружности, а отрезок AB является ее диаметром. - верное числовое равенство, значит точка A принадлежит заданной окружности, а отрезок AB является ее диаметром.
|
4-5 минут
Приложение 1
Совместное решение задачи; одного ученика вызвать к доске для оформления решения задачи.
Поскольку существует две таких касательных, то их уравнения: 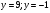
4-5 минут
Приложение 1
Обсудить ход решения задачи с классом (фронтальная беседа). Примерные вопросы:
Как можно доказать, что перед вами уравнение окружности?
Какой отрезок называется диаметром окружности?
Какими свойствами обладает диаметр?
Любой ли отрезок, середина которого совпадает с центром окружности, может являться диаметром этой окружности?
Дети самостоятельно решают задачу; для проверки правильности решения к скрытой доске вызвать одного ученика.
|
4. Домашнее задание.
Обязательное задание.
Повторить весь теоретический материал по темам «Уравнение прямой», «Уравнение окружности».
Решить задачи:
№1. Составьте уравнение прямой, проходящей через начало координат и точку 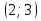 . .
№2. Найдите точки пересечения окружности
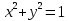 с прямой: а) с прямой: а) 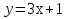 , б) , б) 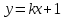 . .
Дополнительная часть.
№3. Найдите периметр треугольника ABC, у которого точка 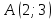 - центр окружности радиуса 2, точка - центр окружности радиуса 2, точка 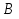 - центр окружности - центр окружности 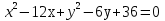 , а точка C – одна из точек пересечения данных окружностей. , а точка C – одна из точек пересечения данных окружностей.
Ответ: 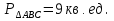
|
2-3- минуты
Приложение 2
Обязательное задание дома выполняют все ученики, а дополнительное задание – по желанию. Можно рассмотреть вариант отдельного оценивания этой задачи.
Ранее учащимся было предложено задание: составить и решить задачу по темам «Уравнение окружности», «Уравнение прямой».
Задача №3 домашней работы – это задача, придуманная одним из учеников.
|
Самостоятельная работа обучающего характера.
Самостоятельная работа проводится в форме теста, состоящего из двух частей: тестовой и части с подробной записью решения. Тексты заданий следует раздать ученикам во время комментариев к домашнему заданию.
Работу учащиеся выполняют на двойных листах.
В журнал следует поставить оценки тем ученикам, которые довольны своим результатом, поскольку самостоятельная работа носит обучающий характер.
|
20 минут
Приложение 3
После того, как ученики сдадут свои работы, при наличии времени можно осуществить мгновенную проверку (слайд 13)
|
Список использованной литературы
Костаева Т.В. Геометрия. Тетрадь с печатной основой 8 класс Изд. 2-ое, доп. И перераб. – Саратов: МВУИП «Сигма - плюс», 1996.
Математика: 2600 тестов и проверочных заданий для школьников и поступающих в вузы / П.И. Алтынов, Л.И. Звавич, А.И. Медяник и др. – 2-е изд., стереотип. – М.: Дрофа, 2000.
Иллюстрации автора, выполнены в программах GeoGebra WebStart и 1C Математический конструктор 3.0.
|
|
|
 Скачать 95.64 Kb.
Скачать 95.64 Kb.

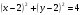
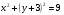
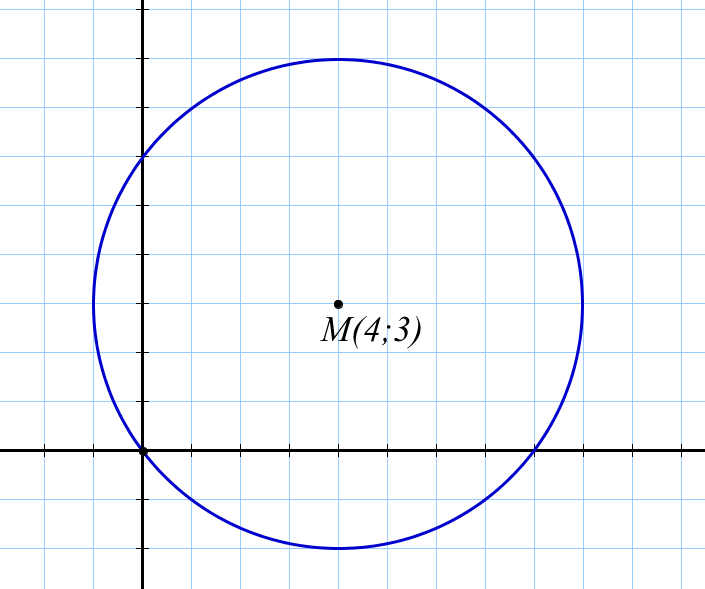
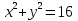 ;
;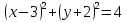 ;
;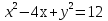 .
.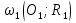 и
и 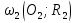 , если
, если 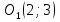 ,
, 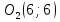 и:
и: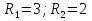 ;
;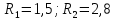 ;
;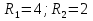 .
.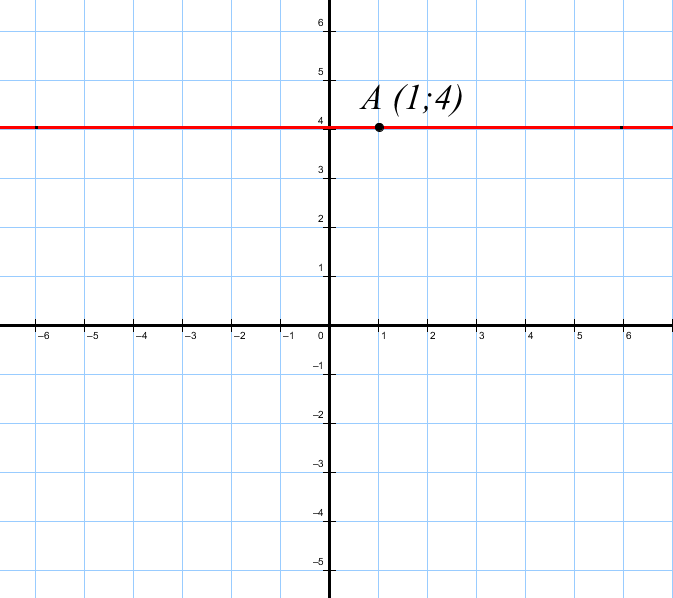
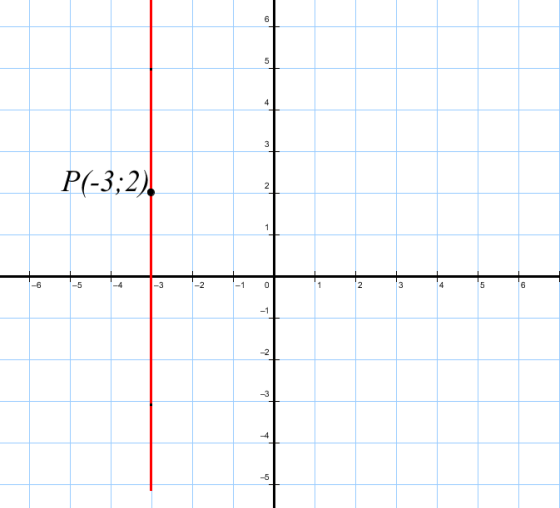
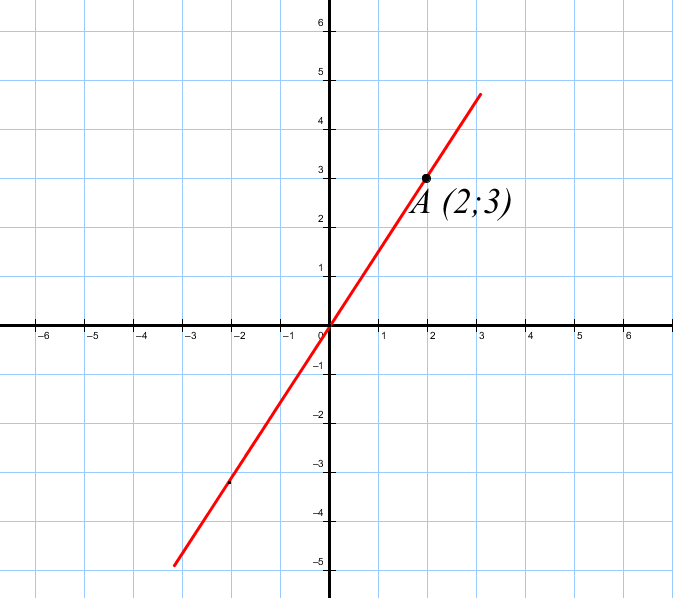



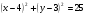
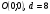 ;
;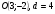 ;
;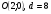 .
.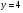 ;
;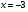 ;
;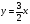 ;
;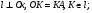
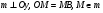 .
.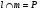 , следовательно точка
, следовательно точка 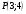 - центр окружности.
- центр окружности.
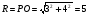 .
.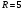 :
: 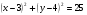
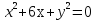 , является окружностью. Является ли отрезок AB, где
, является окружностью. Является ли отрезок AB, где 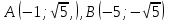 , диаметром этой окружности?
, диаметром этой окружности?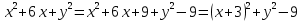 . Тогда исходное уравнение примет вид
. Тогда исходное уравнение примет вид 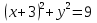 , а это – уравнение окружности с центром в точке
, а это – уравнение окружности с центром в точке 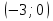 и радиусом равным 3.
и радиусом равным 3. 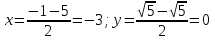 , т.е. координаты середины отрезка AB совпадают с координатами центра заданной окружности.
, т.е. координаты середины отрезка AB совпадают с координатами центра заданной окружности.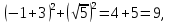
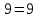 - верное числовое равенство, значит точка A принадлежит заданной окружности, а отрезок AB является ее диаметром.
- верное числовое равенство, значит точка A принадлежит заданной окружности, а отрезок AB является ее диаметром.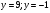
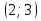 .
.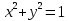 с прямой: а)
с прямой: а) 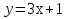 , б)
, б) 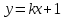 .
.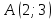 - центр окружности радиуса 2, точка
- центр окружности радиуса 2, точка 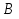 - центр окружности
- центр окружности 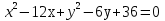 , а точка C – одна из точек пересечения данных окружностей.
, а точка C – одна из точек пересечения данных окружностей.