Держатель для розы кустовой

Держатель для розы кустовой и других цветов от производителя.

armaturakompozit.ru

Урока: "Логарифмическая функция в уравнениях" Математика гимнастика ума. Гимнастика это система упражнений для физического развития человека; гимнаст человек ловкий, стройный, сильный, пластичный, красивый

Название	Урока: "Логарифмическая функция в уравнениях" Математика гимнастика ума. Гимнастика это система упражнений для физического развития человека; гимнаст человек ловкий, стройный, сильный, пластичный, красивый
Дата	05.04.2016
Размер	94.55 Kb.
Тип	Урок

Тема урока: "Логарифмическая функция в уравнениях"

Математика – гимнастика ума.

Гимнастика – это система упражнений для физического развития человека; гимнаст – человек ловкий, стройный, сильный, пластичный, красивый.

Также много даёт математика для умственного развития человека - заставляет думать, соображать, искать простые и красивые решения, помогает развивать логическое мышление, умение правильно и последовательно рассуждать, тренирует память, внимание, закаляет характер.

Цели урока:

1)образовательные:

– обобщить и закрепить понятие логарифма числа;
– повторить основные свойства логарифмов, свойства логарифмической функции;
– закрепить умения применять эти понятия при решении уравнений;

- подготовить к ЕГЭ.

2) воспитательные:

-воспитание познавательной активности, культуры общения, культуры диалога;

3) развивающие:

– развитие зрительной памяти;
– развитие математически грамотной речи, логического мышления, сознательного восприятия учебного материала.

Оборудование урока: доска, мел, карточки для разноуровневой самостоятельной работы.

Тип урока: урок-обобщение

Метод работы: фронтальный опрос, практический, проблемно-поисковый, метод самостоятельной работы.

Ход урока:

Я приветствую Вас на сегодняшнем уроке алгебры. Тема урока: “Логарифмическая функция в уравнениях”. Сегодня мы повторим понятие логарифма числа, свойства логарифма, логарифмической функции, закрепим умения применять эти понятия при решении уравнений.

А начнем урок с умственной разминки. Я этот этап назвала “Потяни за ниточку”.

1. Дайте определение логарифма числа?

Логарифмом числа в по основанию а называется показатель степени, в которую нужно возвести основание а, чтобы получить число в.

2. Как читается основное логарифмическое тождество?

, а

3. Основные свойства логарифмов?

4. Какие логарифмы называются десятичными?

Логарифмы по основанию 10 .

Выполним задания на применение определения логарифма числа. (на доске)

1.	2.
3.	4.
5.	6.
7.	8.

Ответ:1)2; 2)0; 3) -4; 4)4; 5)-3; 6)-3; 7)9; 8)36.

В1
В2
В3
В4
В5
В6
В7
В8

Тренировка заполнения бланков по ЕГЭ.

Следующий этап разминки “ Видит око, да ум ещё дальше”. Выполним задания на применение свойств логарифмов: (на доске)

1.	2.
3.	4.

Ответ: 1)1; 2)1; 3)2; 4)-3.

Предлагаю вашему вниманию “Логарифмическую комедию “2>3”.

Рассмотрение начинается с безусловно правильного неравенства:

. Затем следует преобразование:

, которое также не внушает сомнения. Большему числу соответствует больший логарифм, значит

После сокращения на

, имеем 2>3. В чем состоит ошибка этого доказательства?

Ответ: Ошибка была допущена при сокращении на

; т.к.

<0, то при сокращении на

необходимо было изменить знак неравенства, т.е. 2<3.

Следующий этап урока называется “На приз Непера”.

Немного об изобретателе логарифмов и создателе логарифмических таблиц. Джон Непер- шотландец. В 16 лет отправился на континент, где в течение 5 лет учился в различных университетах Европы, изучал математику. Затем серьезно занимался астрономией и математикой. К идее логарифмических вычислений непер пришел ещё в 80-х годах 16 века, однако опубликовал свои таблицы только в 1614г., после 25-летних вычислений. Они вышли под названием “Описание чудесных логарифмических таблиц”. Неперу принадлежит и сам термин “логарифм”, который он переводит как “искусственное число”. Таблицы и идеи Непера быстро нашли распространение. “Правило Непера” и “аналогии Непера” можно встретить в так называемой сферической тригонометрии. (Белецкая Люба)

Сейчас проведем графический диктант “Логарифмическая функция”. Я буду читать вопросы, вы, отвечая в тетради на вопрос в строчку изобразите ответ, где “Да” изобразите отрезком

, а “нет” уголком

. В результате ответов на вопросы у вас получится “график”.

Вопросы – задания (читает учитель).

1. Логарифмическая функция

определена при любом х (нет)

2. Функция

логарифмическая при

(да)

3. Областью определения логарифмической функции является множество действительных чисел (нет)

4. Областью значений логарифмической функции является множество действительных чисел (да)

5. Функция

– возрастающая (да)

6. График функции

пересекается с осью Ох (да)

7. Существует логарифм отрицательного числа (нет)

В результате выполнения диктанта в тетрадях станет такая запись.

Ответ:

Продолжаем урок. И следующий этап урока “ Доберись до вершины”.

Применим свойства логарифма к решению логарифмических уравнений. Разберем решение логарифмического уравнения методом введения переменной.

Решим № 520 г.

1) г)

ОДЗ: х>0

Пусть

Д=4+12=16

х=27

Ответ:

.

2) №518г.

ОДЗ:

или

(не входит в ОДЗ)

Ответ: 0

3) №523в.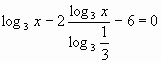

ОДЗ:

Ответ: 9

Караоке.

Ученикам предлагается решить уравнения и про полученное в ответе число напеть строчку из песни, где оно встречается.

1. log _1/2 x = -1 (х=2, “Дважды два – четыре, дважды два – четыре…”)

2. log ₃ x = 1 (х=3, “Три танкиста, три веселых друга, экипаж машины боевой…”)

3. lg x = 6 (х=1000000, “Миллион, миллион алых роз…”)

4. log ₂₀₀₆ x = 0 (х=1, “Ты единственная моя…”)
А этот этап урока называется “Для везунчиков!”

Ребята! Вам очень повезло. В этом году вы участвуете в ЕГЭ. Я предлагаю вам выполнить самостоятельную работу. У вас на столе лежат варианты самостоятельных работ.(Приложение №1)
Продолжите фразу:
“Сегодня на уроке я научился…”
“Сегодня на уроке я познакомился…”
“Сегодня на уроке я повторил…”
“Сегодня на уроке я закрепил…”
Оценки:

Домашнее задание: повторить темы: “Логарифмическая функция, ее свойства, график”, карточки разноуровневые

Приложение №1

Вариант №1

1. Решите уравнение