Урок в 11 а классе по алгебре и началам анализа. ( Физико-математическая группа) Тема: Решение нестандартных показательных уравнений. Тип урока : Комбинированный
 Скачать 75.46 Kb. Скачать 75.46 Kb. |
             Открытый урок в 11 а классе по алгебре и началам анализа. ( Физико-математическая группа) Тема: Решение нестандартных показательных уравнений. Тип урока: Комбинированный. Цель урока: а) Ознакомить учащихся с некоторыми типами показательных уравнений и нестандартны методами их решения; б) углубить знания учащихся по теме: «Показательные уравнения»; в) способствовать формированию умений применять приемы сравнения, обобщения переноса знаний в новую ситуацию; развитию творческих способностей учеников при решении заданий, содержащих параметры. Воспитательная цель: Бережное отношение к нашему общему дому «Земля», экология окружающей среды – здоровье нации. Оборудование: Интерактивная доска, компьютер, листы самоконтроля, маршрутные листы. Изречение на доске: «Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий, кто желает к ним приобщиться, должен достигнуть этого собственной деятельностью, собственными силами, собственным напряжением. Извне он может получить только возбуждение» А.Дистервег. Ход урока. I .Организация урока. Вступление. Математика всегда была неотъемлемой и существенной составной частью человеческой культуры, она является ключом к познанию окружающего мира, этого хрупкого мира планета «Земля», дома в котором мы живем, которого, если не задумываться, можно превратить не в рай, а в человеческие страдания. В конце урока мы с вами к этому вернемся, когда будем решать показательные уравнения, связанные с радиоактивным распадом. И так, показательные уравнения, нестандартные показательные уравнения. Для чего нужны нам эти уравнения?
Но не менее важно развивать в человеке смысл поставленной перед нам задачи, для чего мы это делаем, зачем нам нужны еще показательные уравнения, где они применяются, может мы просто их решаем для умственного развития и закончив школу, сдав успешно экзамен, мы о них и не вспомним. Я думаю, что частично на этот вопрос мы с вами постараемся ответить на этом уроке. А сейчас приступим к нашему уроку «Нестандартные показательные уравнения», они называются еще трансцендентными уравнениями, и методы их решения .А пока мы с вами проверим домашнее задание. II .Проверка домашнего задания: Решить уравнения: 1) 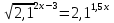 Ответ: -3. Ответ: -3.2) 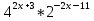 = 32 Ответ: 5. = 32 Ответ: 5.3) 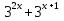 = 18 Ответ: 1. = 18 Ответ: 1.4) 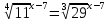 Ответ: 7. Ответ: 7.Найти наибольший корень уравнения: 5) 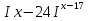 =1 Ответ: 25. =1 Ответ: 25.( На доске примеры и ответы и идет взаимопроверка, учащиеся выставляют оценки на листах самоконтроля). III. Повторение теоретического материала.
1) Какая функция называется показательной? 2) Какими свойствами обладает показательная функция? 3) Какова ее область определения? 4) Какова область изменения? 5) Какова показательная функция по монотонности? 6) Возрастает или убывает функция и почему? а) У= 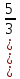 , б) у = , б) у = 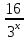 , в) у = , в) у =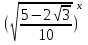 . .6) Сформулируйте теорему о корне.
1 ) 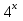 = 32 ( Способ уравнивания показателей), он основан на том , что = 32 ( Способ уравнивания показателей), он основан на том , что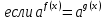 , ,( а 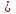 0) , то 0) , то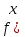 ) = ) = 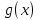 ; ;2) 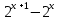 = 16 ( вынесение общего множителя за скобки и снова уравнивание показателей); = 16 ( вынесение общего множителя за скобки и снова уравнивание показателей);3) 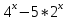 + 6 = 0 (введение новой переменной и решение квадратного уравнения, причем + 6 = 0 (введение новой переменной и решение квадратного уравнения, причем 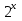 = t , где t = t , где t 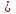 0, и снова уравнивание показателей); 0, и снова уравнивание показателей);4) 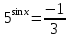 ( нет решений) ; ( нет решений) ;5) 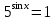 ( уравнивание коэффициентов и простейшее тригонометрическое уравнение) ; ( уравнивание коэффициентов и простейшее тригонометрическое уравнение) ;6) 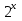 = 1 – х ( функционально-графический метод); = 1 – х ( функционально-графический метод);7) 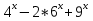 = 0 ( однородное уравнение, делим на = 0 ( однородное уравнение, делим на 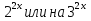 И замена переменной). И замена переменной).IV. Изучение нового материала. Решение нестандартных показательных уравнений. Решить уравнение: 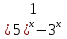 = 16 (Учитель на доске записывает уравнение и ставит вопрос: «Какому типу знакомых уже нам уравнений принадлежит это уравнение и как его решить?»). = 16 (Учитель на доске записывает уравнение и ставит вопрос: «Какому типу знакомых уже нам уравнений принадлежит это уравнение и как его решить?»).Решение: Подбором видно, что х=2 – корень уравнения. Сделаем проверку 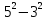 = 16. = 16.А может, есть еще и другие корни уравнения. Докажем, что других корней нет. 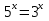 + 16. Разделим данное уравнение на + 16. Разделим данное уравнение на 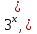 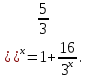 Рассмотрим функцию Рассмотрим функцию 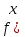 )= )=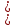 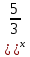 - возрастающая на R, а - возрастающая на R, а 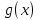 = = 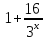 - убывающая на R (почему?). - убывающая на R (почему?).Если одна функция убывающая, а другая возрастающая , то у них только одна точка пересечения, а значит уравнение имеет только один корень. Это уравнение не сложное, но требует доказательства , что других корней нет, знания свойств показательной функции. Уравнений, которые решаются подбором очень много на ЕГЭ. Ответ:2 Устно: решить уравнение 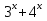 = 25 (объяснение решения). Х=2. = 25 (объяснение решения). Х=2.2) Решить уравнение 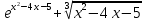 = =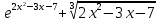 . .Теорема: Пусть R – область определения функции 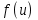 и пусть эта функция непрерывна и строго монотонна на R , тогда равносильны уравнения и пусть эта функция непрерывна и строго монотонна на R , тогда равносильны уравнения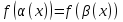 и и 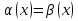 . Применяя эту теорему, имеем: . Применяя эту теорему, имеем: 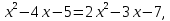 х=-2 и х=1. х=-2 и х=1.Ответ: -2; 1. Самостоятельно: Решить уравнение 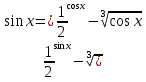 . .Решение: 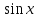 = =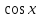 -однородное тригонометрическое уравнение. -однородное тригонометрическое уравнение.tg(х) = 1 , х= 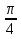 + πп , где п + πп , где п 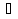 Z . Z .Ответ: 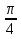 + πп , где п + πп , где п 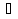 Z . ( взаимопроверка на листах самоконтроля ) Z . ( взаимопроверка на листах самоконтроля )3) Решить уравнение 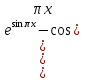 =0 . Это уравнение решается с помощью свойства неотрицательности функции. =0 . Это уравнение решается с помощью свойства неотрицательности функции.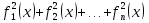 = 0 или = 0 или 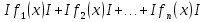 = 0, то = 0, то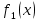 = 0, = 0,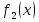 =0 , =0 ,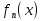 = 0. = 0.Значит, 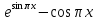 = 0 , = 0 , 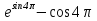 = 0 , = 0 ,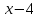 = 0; х = 4 . = 0; х = 4 .Подставив х = 4 в первое уравнение видно, что х = 4 – корень уравнения. ( Легче всего решать всегда нужно уравнение нам уже знакомое, х-4=0, а поскольку мы решаем систему уравнений, то корень простого уравнения подставляем в уравнение нестандартное). Такие уравнения очень часто тоже встречаются на ЕГЭ. Ответ: 4. Самостоятельно: Решить уравнение ( 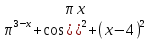 = 0. = 0.Ответ: 3. 4) Решить уравнение 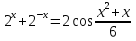 . Это уравнение решается с использованием числовых неравенств, а именно . Это уравнение решается с использованием числовых неравенств, а именно а + 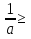 2 – сумма двух взаимообратных чисел , причем если а=1 то а + 2 – сумма двух взаимообратных чисел , причем если а=1 то а + 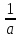 = 2 , остальных случаях неравенство больше 2. = 2 , остальных случаях неравенство больше 2.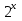 + + 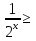 2, 2, 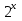 + + 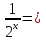 2, 2, 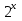 = 1 , х=0 , = 1 , х=0 ,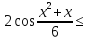 2; 2;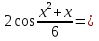 2; 2;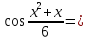 1 ; 1 ;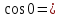 1. 1.Ответ: 0. Самостоятельно: 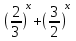 = 2 – = 2 –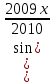 . .Ответ: 0. 5) При каких значениях параметра «в» уравнение имеет два различных корня 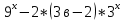 + 5 + 5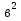 - 4в =0. - 4в =0.Решение. Ученик у доски решает уравнение с помощью учителя. Обозначим 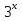 = t , = t ,  t t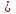 0. 0.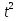 - 2*(3в-2) t + 5 - 2*(3в-2) t + 5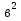 - 4в = 0. Для того , чтобы показательное уравнение имело два корня , - 4в = 0. Для того , чтобы показательное уравнение имело два корня , 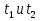 должны быть положительны . Так как оба корня положительны , то необходимо и достаточно, чтобы выполнялась следующая система неравенств: должны быть положительны . Так как оба корня положительны , то необходимо и достаточно, чтобы выполнялась следующая система неравенств:Д 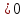 , 2 , 2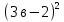 - 4(5 - 4(5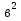 -4в) -4в)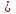 0, 4 0, 4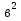 - 8в + 4 - 8в + 4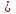 0, 0, 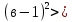 0 , в 0 , в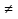 1, 1,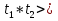 0, 5 0, 5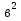 - 4в - 4в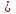 0, в 0, в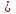 0, в 0, в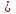 0,8 ; в 0,8 ; в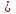 0,8. 0,8.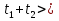 0; 2(3в-2) 0; 2(3в-2)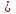 0; в 0; в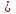 0,8; 0,8;в 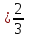 ; ;Ответ: (0,8; 1) 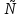 (1; ∞) (1; ∞) Мы решали в течение урока трансцендентные показательные уравнения, требующие нестандартного подхода к их решению. Но я вам обещала в начале урока показать их практическое применение. В новой версии ЕГЭ есть такая задача: Масса радиоактивного вещества уменьшается по закону m(t)= 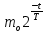 . В лаборатории получили вещество, содержащее в начальный момент времени . В лаборатории получили вещество, содержащее в начальный момент времени 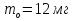 изотопа натрия-24 , период полураспада которого Т=15часов. Через сколько часов содержание натрия-24 будет 3мг? изотопа натрия-24 , период полураспада которого Т=15часов. Через сколько часов содержание натрия-24 будет 3мг?Решение. 12* 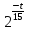 = 3 , = 3 , 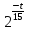 = = 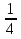 , , 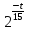 = = 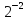 , , 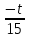 = -2 , t = 30(часов). = -2 , t = 30(часов).Ответ: 30часов. Вот вам и практическое применение показательных уравнений. А для чего применяется в жизни радиоактивный распад и радиоактивные вещества ? Большую помощь приносят людям радиоактивные вещества в медицине при лечении одного из самых страшных заболеваний онкологии, при строительстве атомных электростанций и других промышленных отраслях. Но не надо забывать, что радиоактивные вещества приносят и огромный вред, если к ним прикасаются недобросовестные, безответственные и амбициозные люди. Вспомните, сколько горя людям принесла авария Чернобыльской атомной станции. Люди до сих пор ощущают последствие этой аварии и будут еще долго ее ощущать. А атомная бомба, сброшенная на Японские города Хиросима и Нагасаки. Самое страшное, что собрать то, что выброшено в атмосферу, никак нельзя. А то, что попало в землю распадается в течение многих сотен лет. Так распад урана составляет 7, 04* 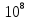 лет или 704.000.000 лет, это означает, что на протяжении сотни миллионов лет уран будет излучать радиацию, опасные для жизни, пока не превратится через миллионы лет в свинец, безопасный для жизни. лет или 704.000.000 лет, это означает, что на протяжении сотни миллионов лет уран будет излучать радиацию, опасные для жизни, пока не превратится через миллионы лет в свинец, безопасный для жизни.Решить уравнения: Домашнее задание 1) 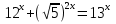 ; ;2) 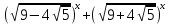 = 18 ; = 18 ;3) При каких значениях параметра «а» уравнение имеет единственное решение? 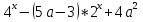 - 3а = 0; - 3а = 0;4) 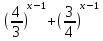 = 1 + = 1 + 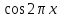 ; ;5) 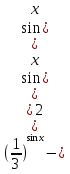 Муниципальное образовательное учреждение «Средняя общеобразовательная школа №1 п. Пангоды» Конспект урока по алгебре и началам анализа в 11 классе по теме «Решение нестандартных показательных уравнений» Учитель математики Дрожина В.И. 2010 год |