«Решение показательных уравнений»
 Скачать 74.47 Kb. Скачать 74.47 Kb.
|
| Конспект урока алгебры и начала анализа в 11 классе (профильный уровень) по теме «Решение показательных уравнений». Цели урока:
УУД обучающихся: 1. Формирование умений и навыков в решении задач по данной теме; 2. Развитие умений анализировать условие задачи и относить ее к тому или иному типу;
Оборудование: мультимедийный проектор, компьютер. Ход урока:
Проверить готовность учащихся к уроку. Дать домашнее задание.
Учитель. Назовите способы решения показательных уравнений. Слайд № 1.  Решите простейшие показательные уравнения и неравенства с пояснением, используя свойства показательной функции. Решите простейшие показательные уравнения и неравенства с пояснением, используя свойства показательной функции.
В классе решаются номера: 12.7 – 12.8(а), 12.11 (а), 12.13 – 12.14 (а), 12.17 – 12.18 (а), 12.22 – 12.23 (а). Решите уравнения. № 12.7 (а) № 12.8 (а) 2 х ∙3/2 х =1/9. (√12) х ∙ (√3) х =1/6. Решение. Решение. (2∙3/2) х= 1/9; (√12 ∙ √3) х = 1/6; 3х = 3‐2; 6х = 6‐1; х = ‐ 2. х = ‐ 1. Ответ. – 2. Ответ. – 1. № 12.11 (а) № 12.13 (а) 3х + 1 ∙ 5х = 675. 2х = 3х. Решение. Решение. 3 ∙ 3х ∙ 5х = 675; Разделим обе части уравнения на 3х 15х = 675 ÷ 3; (2/3) х =1; 15х = 152; (2/3) х = (2/3)0; 15х = 225; х=0. х=2. Ответ: 2. Ответ:0. Динамическая пауза (1 минута). № 12.14(а) № 12.17 (а) 3 х ∙ 7 х + 2 = 49 ∙ 4 х. 3х – 3 х + 3 = ‐78. Решение. Решение. 3х ∙ 7х ∙ 49 = 49 ∙ 4х; 3х – 3х ∙ 27 = ‐ 78; 21х =4 х 3х ∙ ( 1 – 27 ) = ‐78; Разделим обе части уравнения 3х = 3; на 4х, получим: х = 1. (21/4)х = 1; х = 0. Ответ: 0. Ответ: 0. № 12.18 (а) № 12.22 (а) 72х + 1 + 72х + 2 + 72х +3 = 57. 2 ∙ 4х – 5 ∙ 2 х +2=0 Решение. Решение. 72х +1 ∙ (1 + 7 + 49 ) = 57; 2 ∙ 2 2х – 5 ∙ 2х + 2 = 0. 72х + 1 = 70; Введём замену: 2х = а. 2х + 1 = 0; 2 а2 – 5 а + 2 =0; х = ‐ 0,5. а1 = 2; а2 = 0,5. Ответ. – 0,5. Имеем: 2х = 2; 2х = 0,5; х =1; х = ‐1. Ответ. ±1. № 12.23 (а) 4∙(1/16) х – 17(¼) х + 4 = 0. Решение. Введём замену: (¼)х = с 4 с2 – 17 с + 4 = 0; с1=4; с2 = ¼; Имеем: (¼)х = 4; (¼)х =1/4; х = ‐ 1; х = 1. Ответ. ±1. 5.Тестирование (12 – 14 минут). 1 вариант.
1) ‐1 2) 1 3) 7 4) ‐7
1) 11 2)0 3) ‐11 4)0; 11 3. Найдите сумму корней уравнения: 3–х2 – 2 х + 12 = 9х. 1) 4 2) 8 3) ‐4 4) ‐8 4. Укажите промежуток, содержащий корень уравнения : 750 = 6 ∙ 51+2х. 1) (‐2;2) 2) [2;3] 3) (‐∞;0) 4) (5;6]
2 вариант. 1. Решите уравнение: 34‐х = 27. 1) 1 2) 4 3) ‐1 4) 0
1) 0,5 2) ‐0,5 3) ‐0,4 4)0,4
1) √5/5 2) - √5/5 3)1 4) 0 4. Укажите промежуток, содержащий корень уравнения:4/22х =1/32 1) 1) [‐3,5;0) 2) [0;2) 3) [3,5;4,5] 4) (5;8) 5. Решите уравнение: 7292х+1 = 1/27 х После сдачи работ учащиеся могут сделать самопроверку. Слайд № 2.
Литература.
В 2 ч. Ч. 2. Задачник для общеобразовательных учреждений (профильный уровень) / [А. Г. Мордкович и др.]; под ред. А. Г. Мордковича. – М.: Мнемозина, 2007. |
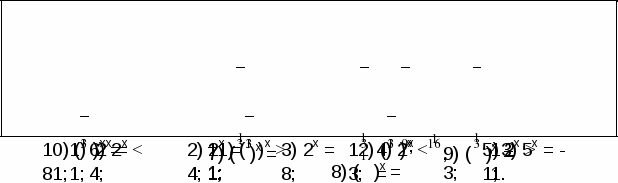 (20– 22 минуты).
(20– 22 минуты).