Урок по теме : «Решение тригонометрических и комбинированных уравнений. Задания С1 егэ.»
 Скачать 55.49 Kb. Скачать 55.49 Kb.
|
| Урок по теме : «Решение тригонометрических и комбинированных уравнений. Задания С1 ЕГЭ.» (11-й класс) Учитель математики МБОУ СОШ №2 имени Луначарского станицы Медведовской Тимашевский район Краснодарский край Козляковская Лидия Сергеевна Цели урока: Образовательные: Систематизировать и обобщить умения и навыки решения тригонометрических и комбинированных уравнений типа; проводить отбор корней разными способами. Развивающие: развивать познавательный интерес, логическое мышление, внимание, навыки самоконтроля. Воспитательные: воспитывать трудолюбие, аккуратность при выполнении вычислений, прививать интерес к математике Задачи урока: проверить знания учащихся по освоению основных приемов решения тригонометрических и комбинированных уравнений; научить творчески применять свои знания при решении заданий типа С1 ЕГЭ. Тип урока: закрепление и систематизация знаний по теме. Подготовка к ЕГЭ. Формы урока: коллективная, индивидуальная, групповая. Оборудование: мультимедийный проектор, ноутбук, презентация, карточки с заданиями, документ-камера. Ход урока: 1.Организационный вопрос. Накануне были выбраны 2 команды учеников по 6 человек. Они получили все задание на дом: решить 3 уравнения повышенной сложности. Класс разбит на 3 группы: 2 команды игроков и 1 команда болельщиков. Учитель: Добрый день, ребята. До экзаменов осталось совсем немного времени. Мы сегодня подведем итоги, чему научились в течение учебного года. А решать мы будем задания, связанные с тригонометрическими, показательными и логарифмическими уравнениями. Мы с вами поиграем в математические игры, но самое главное начнется в середине урока, когда команды покажут свое искусство и изящество в решении задач. 2.Устный счет. От каждой команды вызываются к доске по ученику и ваша задача: Собрать математическое домино из формул. (Выдаются 14 карточек на знание формул тригонометрии) (слайд3) 2 болельщиков в режиме онлайн решают задания ЕГЭ на ноутбуках.(20мин) В это же время все остальные учащиеся работают с учителем. Решают устно. 1. Может ли синус угла быть равным: а) -3,7; б) 3,7; в) 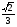 ; г) ; г) 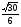 ? ?2. Может ли косинус угла быть равным: а) 0,75; б) 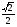 ; в) -0,35; г) ; в) -0,35; г)  ? ?3. При каких значениях а и b справедливы следующие равенства: cos   sin sin tg tg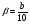 sin  ctg ctg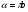 cos cos 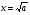 4. Является ли число π корнем уравнения: а) 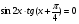 ; б) ; б)  ? ?3.Мозговой штурм. Кто первым начнет рассказывать решение задач - зависит от капитанов команд. Капитаны получают задание на доске. Решить уравнения:
Кто из капитанов быстрее и правильно решит пять уравнений, та команда начнет первый ход. 4.Математический бой. Решение уравнений С1.Команда может предложить противнику показать решение одной из 3 задач.(правила матбоя в приложении). Решить уравнения:
б) Найдите корни этого уравнения, принадлежащие промежутку [-2π; -π] Решение. а) Преобразуем уравнение, применим формулы двойного аргумента и формулы приведения, получим 2cos2x-1=cosx 2cos2x-cosx-1=0 Пусть cosx=t, где -1≤ t ≤1, тогда уравнение примет вид 2 t2-t-1=0 D=(-1)2-4*2*(-1)=9 t1 = 1 или t2 = - 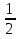 . .Значит, соsx=1 , х=2πn, nϵZ; или cosx= - 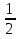 , х= , х=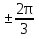 + πn,nϵZ. + πn,nϵZ.б)Отберем с помощью единичной окружности корни уравнения, принадлежащие промежутку [-2π; -π]: -2π; -  . .2. а) Решите уравнение 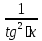 - - 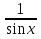 -1=0 -1=0б) Найдите корни этого уравнения, принадлежащие промежутку [-3π; 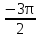 ]. ].Решение. Учитывая, что соsx≠0 и sinx≠0, получаем 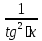 = =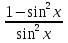 = = - 1 - 1Уравнение примет вид  -2=0 -2=0Пусть 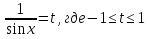 , тогда t2-t-2=0, D=(-1)2-4*1*2=9 , t= , тогда t2-t-2=0, D=(-1)2-4*1*2=9 , t=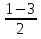 =-1; t= =-1; t=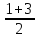 =2. =2.Получим, 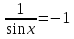 или или  , откуда , откуда 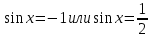 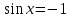 не удовлетворяет условию соsx≠0, отсюда не удовлетворяет условию соsx≠0, отсюда 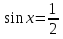 ; ;х = 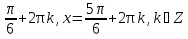 . .б)Отберем с помощью единичной окружности корни, принадлежащие промежутку [-3π; 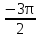 ]. ].х=- 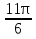 . .Ответ :а) х = 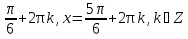 . ;б) х=- . ;б) х=- 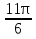 . .3.а)Решите уравнение 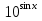 = = 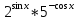 б) Найдите корни этого уравнения, принадлежащие промежутку [-  ;- π]. ;- π].Решение. а) Преобразуем исходное уравнение 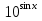 = = 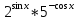 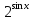 * *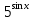 = =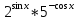 ; ; 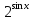 >0; >0;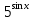 = =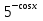 ; ;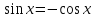 ; ;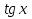 =-1; =-1;х= 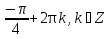 . .б) Отберем корни, принадлежащие промежутку [-  ;- π]. ;- π]. Получим числа -  ;- ;-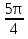 . .Ответ: а) х= 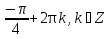 ; б) - ; б) -  ;- ;-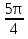 . .5.Физкультминутка. 6.Блиц-турнир. Учитель: Обе команды и болельщики получают задание .Время 10 минут. Проверка решения с помощью документ - камеры. Решите уравнение ( 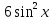 + 5 + 5  -4) -4)  =0 =0(ответ : х= 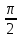 +πn, nϵZ,x= +πn, nϵZ,x= +2πk, kϵZ) +2πk, kϵZ)7.Подведение итогов. Выставление оценок. 8.Рефлексия. 1. Сегодня я узнал… 2. Было интересно… 3. Было трудно… 4. Меня удивило 5. Урок дал мне для жизни… 9. Задание на дом : Из открытого банка заданий найти задание С1 , решить и оформить на листе А4.Приготовиться к защите работы. Литература :
|



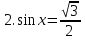
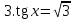

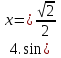

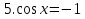
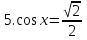
 +2πn, nϵZ; 3)
+2πn, nϵZ; 3)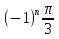 + πn,nϵZ;
+ πn,nϵZ; + πn,nϵZ; 5)π+ πn,nϵZ.
+ πn,nϵZ; 5)π+ πn,nϵZ.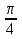 + πn,nϵZ; 4)
+ πn,nϵZ; 4) + πn,nϵZ; 5) ±
+ πn,nϵZ; 5) ±