Урок-конференция
 Скачать 46.83 Kb. Скачать 46.83 Kb.
|
| Урок-конференция. Применение производной в различных областях науки 1)Рассмотрение задач, приводящих к понятию производной. 2)Формирование представлений об общих математических методах в разных отраслях наук. 3)Формирование самостоятельности, умения сформулировать свои мысли. Этот урок требует некоторой подготовки учащихся. Несколько представителей разных отраслей науки рассказывает о своих исследованиях. Учитель обобщает их доклады, указывая, что все рассмотренные задачи требуют для решения одной математической операции. ВСУПИТЕЛЬНОЕ СЛОВО УЧИТЕЛЯ Здравствуйте. (Откройте тетради. Запишите число, классная работа, тему урока.) Тема нашего урока «Применение производной в различных областях науки». И сегодня мы попытаемся, насколько это возможно, в рамках одного урока рассмотреть эту тему. Эпиграфом к нашему уроку хочу взять слова Лобачевского: «…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…» Н.И. Лобачевский Примерное содержание докладов. 1)Физик, изучающий механическое движение Задача о скорости движущейся точки. Пусть s=s(t) представляет закон прямолинейного движения материальной точки. Это уравнение выражает путь s, пройденный точкой, как функция времени t. Обозначим через ∆s путь, пройденный точкой за промежуток времени ∆t от момента t до t+∆t, т.е. ∆s=s(t+∆t)-s(t) Отношение ∆s/∆t называется средней скоростью точки за время от t до t+∆t. Чем меньше ∆t, т.е. чем короче промежуток от t до t+∆t, тем лучше средняя скорость характеризует движение точки в момент времени t. Поэтому естественно ввести понятие скорости U в данный момент t, определив её как предел средней скорости за промежуток от t до t+∆t, когда ∆t→0; Величина U называется мгновенной скоростью точки в данный момент t. 2)Физик, изучающий законы электромагнетизма. Задача о силе электрического тока. Пусть q=q(t) – количество электричества (в кулонах), протекающее через поперечное сечение проводника за время t; Количество электричества есть функция времени, так как каждому значению времени t соответствует определённое значение количества электричества. Для определения скорости изменения количества электричества с течением времени пользуются понятием силы тока. Обозначим через ∆q количество электричества, протекающее через указанное сечение за промежуток времени ∆t от момента t до момента t+∆t. Отношение ∆q/∆t называется средней силой тока за время от t до ∆t и обозначается через Iср. В случае постоянного тока Iср будет постоянной. Если в цепи переменный ток, то Iср будет различна для различных промежутков времени. Поэтому для цепи переменного тока вводят понятие силы тока I в данный момент t, определив её как предел средней силы тока за промежуток времени от t до t+∆t, когда ∆t→0: I = lim ∆t→0 ∆q/∆t Аналогично задаче о скорости прямолинейного движения рассматриваются задачи о скоростях химической реакции и роста популяции, о касательной, о производности труда. 3)Химик. Задача о скорости химической реакции. Пусть дана функция m=m(t), где m – количество некоторого вещества, вступившего в химическую реакцию к моменту времени t. Приращению времени ∆t будет соответствовать приращение ∆m величины m. Отношение – средняя скорость реакции за промежуток времени ∆t. Предел этого отношения при ∆t→0, т.е. lim ∆m/∆t есть скорость химической реакции в данный момент времени t. 4)Математик. Задача о касательной к данной кривой. Пусть на плоскости xOy задана кривая уравнением y=f(x). Требуется провести касательную к данной кривой к данной точке M0(x0;f(x0)). Так как точка касания M0 дана, то для решения задачи потребуется найти угловой коэффициент искомой касательной, т.е. tg 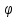 – тангенс угла наклона касательной к положительному направлению оси Ох (рисунок). – тангенс угла наклона касательной к положительному направлению оси Ох (рисунок). Через точки M0(x0;f(x0)) и М`(х0+∆х;f(х0+∆х)) проведём секущую М0М`. Из рисунка видно, что угловой коэффициент tgα секущей M0M` равен отношению tgα= 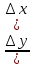 ,где ∆y=f(х0+∆х)-f(x0). ,где ∆y=f(х0+∆х)-f(x0).Угловой коэффициент касательной M0T к данной кривой в точке М0 может быть найден на основании следующего определения: касательная к кривой в точке M0 называется прямая М0Т , угловой коэффициент секущей М0М`, когда ∆x→0. Отсюда следует что tg 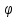 =lim tgα ∆x→0=lim =lim tgα ∆x→0=lim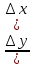 ∆x→0 ∆x→05)Экономист. Задача о производительности труда. Пусть к моменту времени t (часов) рабочий произвёл F=F(t) единиц продукции (выработка составила F(t) единиц). Приращение выпуска продукции ∆F за время ∆t равно числу единиц продукции, выпущенной за время ∆t, т.е. ∆F=F(t+∆t)-F(t). Отношение называется средней производительностью труда рабочего за время t до t+∆t. Предел этого отношения при стремлении ∆t к нулю, т.е. называется производительностью труда рабочего в момент времени t. Дифференциальное исчисление- это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники. Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д. Мы убедились в важности изучения темы "Производная", ее роли в исследовании процессов науки и техники, в возможности конструирования по реальным событиям математические модели, и решать важные задачи. |