Учебник для учащихся общеобразовательных учреждений, часть 1, Задачник для учащихся общеобразовательных учреждений, часть 2/А. Г. Мордкович М.: Мнемозина, 2009
 Скачать 425.02 Kb. Скачать 425.02 Kb.
|
| Пояснительная записка Рабочая программа по математике для 9 класса составлена на основе федерального компонента государственного стандарта основного общего образования (приказ Минобразования России от 5 марта 2004 года № 1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования»), федерального базисного учебного плана для общеобразовательных учреждений Российской Федерации, учебного плана образовательного учреждения с использованием программы по алгебре (автор А.Г.Мордкович) и программы по геометрии для учебника Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева и др. Программа состоит из следующих блоков: титульный лист; пояснительная записка; «учебно-тематический план»; содержание программы; требования к уровню подготовки обучающихся; список литературы; календарно-тематическое планирование, контрольные материалы. Цель рабочей программы - планирование, организация и управление учебным процессом по математике. Задачи учебной рабочей программы - определить содержание, объем, порядок изучения учебного предмета «Математика» с учетом особенностей учебного процесса образовательного учреждения и контингента обучаемых. Данная программа ориентирована на учащихся 9 классов общеобразовательного учреждения, обучение организовано по следующим учебным пособиям: 1. Алгебра 9 класс: Учебник для учащихся общеобразовательных учреждений, часть 1, Задачник для учащихся общеобразовательных учреждений, часть 2/А.Г.Мордкович – М.: Мнемозина, 2009. 2. Геометрия, 7 – 9: Учебник для общеобразовательных учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2007. Согласно базисному учебному плану школы, рекомендациям Министерства образования Российской Федерации выбрана данная учебная программа и учебно-методический комплект. Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
В соответствии с федеральным базисным учебным планом для образовательных учреждений Российской Федерации на изучение математики в 9 классе отводится 5 часов в неделю, всего по 170 часов в год. По одному часу добавляется из компонента образовательного учреждения. В связи с увеличением количества часов, отводимых на изучение курса математики в 7-9 классах, автор учебника алгебры разработал тематическое планирование в двух вариантах (3 и 4 часа в неделю). Расширенное изучение некоторых тем связано со сложностью материала, необходимостью дополнительной отработки вопросов при подготовке к итоговой аттестации. Курс математики 9 класса состоит из следующих предметов: «Алгебра», «Геометрия», которые изучаются блоками. В соответствии с этим составлено тематическое планирование. Основная форма организации образовательного процесса – классно-урочная система. Предусматривается применение следующих технологий обучения: исследовательской, игровой, ИКТ, уровневой дифференциации, проблемного обучения и проектной деятельности. Промежуточная аттестация проводится в форме тестов, самостоятельных, проверочных, контрольных работ и математических диктантов. Календарно-тематическое планирование составлено на 204 урока. Пояснительная записка Рабочая программа по математике для 7-9 классов составлена на основе федерального компонента государственного стандарта основного общего образования (приказ Минобразования России от 5 марта 2004 года № 1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования»), федерального базисного учебного плана для общеобразовательных учреждений Российской Федерации, учебного плана образовательного учреждения с использованием программы по алгебре для 7, 8, 9 классов (автор А.Г.Мордкович) и программы по геометрии для учебника Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева и др. Программа состоит из следующих блоков: титульный лист; пояснительная записка; «учебно-тематический план»; содержание программы; требования к уровню подготовки обучающихся; список литературы; календарно-тематическое планирование, контрольные материалы. Цель рабочей программы - планирование, организация и управление учебным процессом по математике. Задачи учебной рабочей программы - определить содержание, объем, порядок изучения учебного предмета «Математика» с учетом особенностей учебного процесса образовательного учреждения и контингента обучаемых. Данная программа ориентирована на учащихся 7-9 классов общеобразовательного учреждения, обучение организовано по следующим учебным пособиям: 1.Алгебра 7 класс: Учебник для учащихся общеобразовательных учреждений, часть 1, Задачник для учащихся общеобразовательных учреждений, часть 2/А.Г.Мордкович – М.: Мнемозина, 2009. 2.Алгебра 8 класс: Учебник для учащихся общеобразовательных учреждений, часть 1, Задачник для учащихся общеобразовательных учреждений, часть 2/А.Г.Мордкович – М.: Мнемозина, 2009. 3.Алгебра 9 класс: Учебник для учащихся общеобразовательных учреждений, часть 1, Задачник для учащихся общеобразовательных учреждений, часть 2/А.Г.Мордкович – М.: Мнемозина, 2009. 4. Геометрия, 7 – 9: Учебник для общеобразовательных учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2007. Согласно базисному учебному плану школы, рекомендациям Министерства образования Российской Федерации выбрана данная учебная программа и учебно-методический комплект. Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
В соответствии с федеральным базисным учебным планом для образовательных учреждений Российской Федерации на изучение математики в 7, 8, 9 классах отводится по 5 часов в неделю, всего по 170 часов в год. По одному часу добавляется из компонента образовательного учреждения. В связи с увеличением количества часов, отводимых на изучение курса математики в 7-9 классах, автор учебника алгебры разработал тематическое планирование в двух вариантах (3 и 4 часа в неделю). Расширенное изучение некоторых тем связано со сложностью материала, необходимостью дополнительной отработки вопросов при подготовке к итоговой аттестации. Курс математики 7-9 классов состоит из следующих предметов: «Алгебра», «Геометрия», которые изучаются блоками. В соответствии с этим составлено тематическое планирование. Контрольных работ в 7 классе – 12: по геометрии – 5, по алгебре – 7, из них одна итоговая; в 8 классе - 14: по геометрии – 5, по алгебре – 9, из них одна итоговая, в 9 классе – 11: по геометрии – 4, по алгебре – 7, из них одна итоговая. Основная форма организации образовательного процесса – классно-урочная система. Предусматривается применение следующих технологий обучения: исследовательской, игровой, ИКТ, уровневой дифференциации, проблемного обучения и проектной деятельности. Промежуточная аттестация проводится в форме тестов, самостоятельных, проверочных, контрольных работ и математических диктантов. Календарно-тематическое планирование составлено на 204 урока в каждом классе. Литература
Составитель: Т.А. Бурмистрова. - М.: Просвещение, 2009.-125с.
Изучение геометрии в 7 – 9 классах. Методические рекомендации к учебнику. Книга для учителя / Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков- М: Просвещение, 2004.-254с.
СОДЕРЖАНИЕ ПРОГРАММЫ 7 класс Математический язык. Математическая модель (13 ч) Числовые и алгебраические выражения. Переменная. Допустимые значения переменной. Недопустимые значения переменной. Первые представления о математическом языке и о математической модели. Линейные уравнения с одной переменной. Линейные уравнения как математические модели реальных ситуаций. Координатная прямая, виды промежутков на ней. Линейная функция (11 ч) Координатная плоскость. Алгоритм отыскания координат точки. Алгоритм построения точки в прямоугольной системе координат. Линейные уравнения с двумя переменными. Решение уравнения ах + ву + с = 0.График уравнения. Алгоритм построения графика уравнения ах + ву + с = 0. Линейная функция. Независимая переменная (аргумент). Зависимая переменная. Наибольшее и наименьшее значения линейной функции на заданном промежутке. Возрастание и убывание линейной функции. Область определения функции, способы задания функции. Функция y=kx и её график. Взаимное расположение графиков линейных функций. Системы двух линейных уравнений с двумя переменными (13 ч) Система уравнений. Решение систем уравнений. Графический метод решения систем уравнений. Метод подстановки. Метод алгебраического сложения. Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций (текстовые задачи). Степень с натуральным показателем (6 ч) Степень. Основание степени. Показатель степени. Свойства степени с натуральным показателем. Умножение и деление степеней с одинаковыми показателями. Степень с нулевым показателем. Одночлены. Операции над одночленами (8 ч) Одночлен. Коэффициент одночлена. Стандартный вид одночлена. Подобные одночлены. Сложение и умножение одночленов. Возведение одночлена в натуральную степень. Деление одночлена на одночлен. Многочлены. Арифметически операции над многочленами (15 ч) Многочлен. Члены многочлена. Двучлен. Трехчлен. Приведение подобных членов многочлена. Стандартный вид многочлена. Сложение и вычитание многочленов. Умножение многочлена на одночлен. Умножение многочлена на многочлен. Квадрат суммы и квадрат разности. Разность квадратов. Разность кубов и сумма кубов. Деление многочлена на одночлен. Разложение многочленов на множители (18ч) Вынесение общего множителя за скобки. Способ группировки. Разложение многочленов на множители с помощью формул сокращенного умножения, комбинации различных приемов. Метод выделения полного квадрата. Понятие алгебраической дроби. Сокращение алгебраической дроби. Тождество. Тождественные преобразования. Функция у = х² (9ч) Функция у = х², ее свойства и график. Функция у = -х², ее свойства и график. Графическое решение уравнений. Кусочная функция. Чтение графика функции. Область определения функции. Первые представления о непрерывной функции. Точка разрыва. Разъяснения смысла записи у = f(х). Функциональная символика. Начальные геометрические сведения (10ч) Простейшие геометрические фигуры: прямая, точка, отрезок, луч, угол. Понятие равенства геометрических фигур. Сравнение отрезков и углов. Измерение отрезка, длина отрезка. Измерение углов. Градусная мера углов. Вертикальные и смежные углы, их свойства. Перпендикулярные прямые. Треугольники (17ч) Треугольник. Признаки равенства треугольников. Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника. Равнобедренный треугольник и его свойства. Задачи на построение с помощью циркуля и линейки. Параллельные прямые (13ч) Признаки параллельности прямых. Аксиомы параллельных прямых. Свойства параллельных прямых. Соотношения между сторонами и углами треугольника (18ч) Сумма углов треугольника. Соотношение между сторонами и углами треугольника. Неравенство треугольника. Прямоугольные треугольники, их свойства и признаки равенства. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Построение треугольника по трем элементам. Повторение (19ч)
Площадь (14ч) Понятие площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора и теорема обратная теореме Пифагора. Подобные треугольники (19ч) Подобие треугольников. Коэффициент подобия. Связь между площадями подобных фигур. Три признака подобия треугольников. Средняя линия треугольника. Свойство медиан треугольника. Среднее пропорциональное. Пропорциональные отрезки в прямоугольном треугольнике. Измерительные работы на местности. Понятия синуса, косинуса, тангенса острого угла прямоугольного треугольника. Основное тригонометрическое тождество. Значения синуса, косинуса, тангенса углов 30º, 45º, 60º, 90º. Окружность (17ч) Взаимное расположение прямой и окружности. Касательная к окружности, ее свойства и признак. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности. Повторение (21ч) Решение задач по всем темам алгебры и геометрии. 9 класс Рациональные неравенства и их системы (22ч) Линейные и квадратные неравенства (повторение). Рациональное неравенство. Метод интервалов. Множества и операции над ними. Система неравенств. Решение системы неравенств. Системы уравнений (21ч) Рациональное уравнение с двумя переменными. Решение уравнения р(х;у) = 0. Равносильные уравнения с двумя переменными. Формула расстояния между двумя точками координатной плоскости. График уравнения (х – а)2 + (у – в)2 = r2.Система уравнений с двумя переменными. Решение системы уравнений. Неравенства и системы неравенств с двумя переменными. Методы решений систем уравнений (метод подстановки, алгебраического сложения, введения новых переменных). Равносильность систем уравнений. Системы уравнений как математические модели реальных ситуаций. Числовые функции (29ч) Функция. Независимая переменная. Зависимая переменная. Область определения функции. Естественная область определения функции. Область значений функции. Способы задания функции (аналитический, графический, табличный, словесный). Свойства функции (монотонность, ограниченность, выпуклость, наибольшее и наименьшее значения, непрерывность). Исследование функций: у = С, у = кх + т, у = кх2, √у = к/х, у = √х, у = │х│, у = ах2 + вх + с. Четные и нечетные функции. Алгоритм исследования функции на четность. Графики четной и нечетной функции. Степенная функция с натуральным показателем, ее свойства и график. Степенная функция с отрицательным целым показателем, ее свойства и график. Функция у = 3√х, ее свойства и график. |
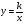 (24ч)
(24ч)