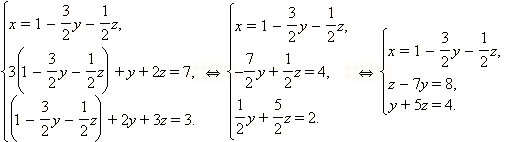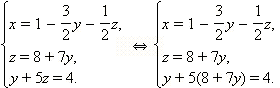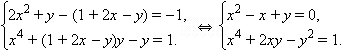Учебник для студентов образовательных учреждений спо/С. Г. Григорьев, С. В. Иволгина; под редакцией В. А. Гусева 10-е изд., стер. М.: Издательский центр «Академия». 2014. 416 с
 Скачать 166.46 Kb. Скачать 166.46 Kb. |
|
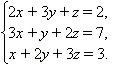 |
Решение:
| Выразим из первого уравнения переменную x: 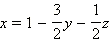 и подставим её во второе и третье уравнения: и подставим её во второе и третье уравнения:
Выразим теперь из второго уравнения переменную
Теперь третье уравнение зависит только от y и мы можем его решить:
Итак, переменная y найдена. По уже полученным формулам для x и z мы можем последовательно их найти:
Ответ. (2; –1; 1). |
Этот метод иногда можно применить и для решения нелинейных систем.
Пример 3
Решить систему уравнений
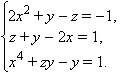 |
Решение:
| Выразим z из второго уравнения: z = 1 + 2x – y и подставим его в первое и третье уравнения. Получим систему из двух уравнений с двумя неизвестными:
Опять из первого уравнения выражаем y (её легче выразить, чем x):
Теперь по найденному x находим y и z:
Ответ. (1; 0; 3), (–1; –2; 1). |
Контрольные вопросы:
понятие определителя n-ого порядка;
методы решения систем линейных уравнений;
решение систем линейных уравнений методом Крамера;
формулы Крамера;
решение систем линейных уравнений методом Гаусса.
Порядок выполнения работы:
Используя теоретические сведения выполнить предложенное преподавателем задание
Соответствующим образом оформить работу
| Лист 1. Практическая работа № 8 по теме « Решение систем линейных алгебраических уравнений различными способами» Выполнил:__________ (ФИО) группа:_____________ Проверил:__________ Оценка:____________ | Лист 2. № примера Решение: Ответ: |
Оформление работы:
Примеры по теме:
Решение систем линейных уравнений методом Крамера
ВАРИАНТ 1
Решить системы:
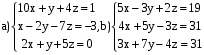
ВАРИАНТ 2
Решить системы:
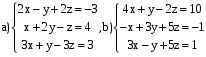
ВАРИАНТ 3
Решить системы:
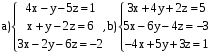
ВАРИАНТ 4
Решить системы:
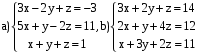
ВАРИАНТ 5
Решить системы:
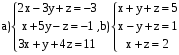
ВАРИАНТ 6
Решить системы:
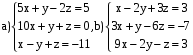
ВАРИАНТ 7
Решить системы:
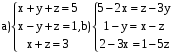
ВАРИАНТ 8
Решить системы:
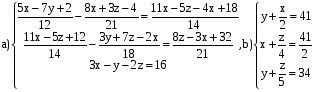
Примеры по теме:
Решение систем линейных уравнений методом Гаусса
ВАРИАНТ 1
Решить системы:
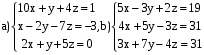
ВАРИАНТ 2
Решить системы:
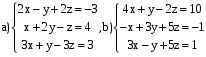
ВАРИАНТ 3
Решить системы:
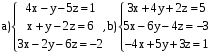
ВАРИАНТ 4
Решить системы:
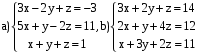
ВАРИАНТ 5
Решить системы:
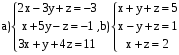
ВАРИАНТ 6
Решить системы:
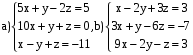
ВАРИАНТ 7
Решить системы:
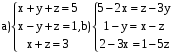
ВАРИАНТ 8
Решить системы:
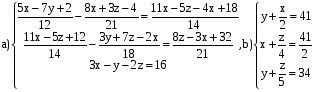
Методические указания по проведению
практической работы № 9
Действия над комплексными числами, заданными в алгебраической форме
Цель работы:
Используя теоретический материал и образцы решения задач, решить примеры по теме «Действия над комплексными числами, заданными в алгебраической форме»
Перечень справочной литературы :
Математика: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, С.В. Иволгина; под редакцией В.А. Гусева – 10-е изд., стер. – М.: Издательский центр «Академия». 2014. – 416 с.
Элементы высшей математики: учебник для студентов образовательных учреждений СПО/С.Г. Григорьев, Ю.А. Дубинский – 9-е изд., стер. – М.: Издательский центр «Академия». 2013. – 320 с.
Шипачев В.С. Основы высшей математика: учебник для вузов. -М. Высш.шк., 2010 г.Шипачев В.С. Задачник по высшей математике: учебное пособие для вузов. -М. Высш.шк., 2010 г.
Краткие теоретические сведения:
Основные понятия
Квадратное уравнение с действительными коэффициентами и отрицательным дискриминантом не имеет действительных корней. Поэтому приходится расширять множество действительных чисел, добавляя к нему новые числа. Эти новые числа вместе с действительными числами образуют множество, которое называют множеством комплексных чисел.
Комплексным числом - называется выражение вида z = a+b i , где a и b действительные числа, число а называется действительной частью комплексного числа z = a+b·i, а число b – его мнимой частью, а i – мнимая единица, определяемая равенством i ² = -1.
Например, действительная часть комплексного числа z = 2+3·i равна a =2, а мнимая равна b = 3.
Действительные числа: z=a+0i=a, z=Re z.
Мнимые числа: z=0+bi=bi, z=Im z.
Равные комплексные числа: z1=a+bi, z2=c+di, z1=z2, если a=c, b=d.
Противоположные комплексные числа: z=a+bi, z=-a-bi.
Сопряженные комплексные числа: z=a+bi, z=a-bi.
Алгебраическая форма записи комплексных чисел: z =a + bi
Сложение и умножение комплексных чисел
Суммой двух комплексных чисел z1=a+b·i и z2= c+d·i называется комплексное число: z = z1 + z2 = (a+b·i ) + ( c+d·i ) = (a+c) + (b+d)·i,
Произведением двух комплексных чисел z1=a+b·i и z2= c+d·i называется комплексное число : z = z1 · z2 =( a+b·i )·( c+d·i )=(a·c – b·d) + (a·d + b·c)·i
Из формул вытекает, что сложение и умножение можно выполнять по правилам действий с многочленами, считая i2= –1. Операции сложения и умножения комплексных чисел обладают свойствами действительных чисел. Основные свойства:
Переместительное свойство:
Z1 +Z2=Z2+Z1, Z1·Z2=Z2·Z1
Сочетательное свойство:
(Z1+Z2)+Z3=Z1+(Z2+Z3), (Z1·Z2)·Z3=Z1·(Z2·Z3)
Распределительное свойство:
Z1·(Z2+Z3)=Z1·Z2+Z1·Z3
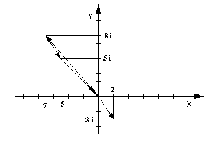
Геометрическое изображение суммы комплексных чисел
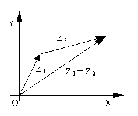
Рисунок 1.
Согласно определению сложения двух комплексных чисел, действительная часть суммы равна сумме действительных частей слагаемых, мнимая часть суммы равна сумме мнимых частей слагаемых. Точно также определяются координаты суммы векторов (Рис.1).
Вычитание и деление комплексных чисел
Вычитание комплексных чисел – это операция, обратная сложению: для любых комплексных чисел Z1 и Z2 существует, и притом только одно, число Z, такое, что: Z + Z2=Z1 Z = Z1 – Z2
Число Z=Z1+(-Z2 )называют разностью чисел Z1 и Z2.
Z= (a+b·i ) - ( c+d·i ) = (a-c) + (b-d)·i,
Деление вводится как операция, обратная умножению: Z×Z2=Z1
Разделив обе части на Z2 получим: Z=
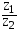
Из этого уравнения видно, что Z2
 0
0Производится умножение делимого и делителя на число, сопряженное делителю. Z=
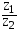 =
= 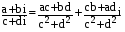
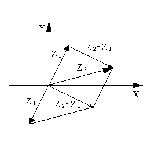
Геометрическое изображение разности комплексных чисел
Рисунок 2
Разности Z2 – Z1 комплексных чисел Z1 и Z2, соответствует разность векторов, соответствующих числам Z1 и Z2. Модуль
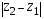 разности двух комплексных чисел Z2 и Z1 по определению модуля есть длина вектора Z2 – Z1. Построим этот вектор, как сумму векторов Z2 и (–Z1) (рисунок 2). Таким образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам.
разности двух комплексных чисел Z2 и Z1 по определению модуля есть длина вектора Z2 – Z1. Построим этот вектор, как сумму векторов Z2 и (–Z1) (рисунок 2). Таким образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам.Примеры вычислений
Пример 1: Найти сумму и произведение комплексных чисел Z1=2 – 3×i и
Z2= –7 + 8×i.
Z1 + Z2 = 2 – 7 + (–3 + 8)×i = –5 + 5×i
Z1×Z2 = (2 – 3×i)×(–7 + 8×i) = –14 + 16×i + 21×i + 24 = 10 + 37×i
Пример 2: Найти сумму и произведение комплексных чисел Z1=1 + 2×i и Z2= 2 - i.
Имеем
Пример 3:
Даны комплексные числа Z1= 4 + 5·i и Z2= 3 + 4·i. Найти разность Z2 – Z1 и частное
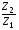
Z2 – Z1 = (3 + 4·i) – (4 + 5·i) = –1 – i
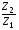 =
=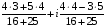 =
=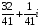
Контрольные вопросы:
понятие комплексного числа (К.Ч.);
алгебраическая форма записи К.Ч;
- арифметические операции над К.Ч.
Порядок проведения работы:
Используя теоретические сведения выполнить предложенный преподавателем вариант задания.
Соответствующим образом оформить работу
| Лист 1. Самостоятельная работа по теме «Действия над комплексными числами» Выполнил:__________ (ФИО) группа:_____________ Проверил:__________ Оценка:____________ | Лист 2. № примера Решение: Ответ: |
Задания
Вариант № 1
Дано комплексное число
Z = 21 – 4 i
Записать число равное, противоположное, сопряженное исходному.
Выполнить действие
Z = ( 3 - 2 i + ( - 6 - 2 i )
Выполнить умножение
Z = ( 3 + 4 i ) ( 1 + 3 i )
Выполнить деление
Z = ( - 6 + 2 i )) : ( 3 - 4 i )
Выполнить действия
Z = ( 5 + 2 i ) : ( 2 - 5 i ) + (7 + 3 i ) : ( 1 - 2 i )
Вариант № 2
Дано комплексное число
Z = 3 + 9 i
Записать число равное, противоположное, сопряженное исходному.
Выполнить действие
Z = ( 5 + 3 i ) + ( - 2 - 5 i )
Выполнить умножение
Z = ( -2 + 3 i ) ( -1 - 6 i )
Выполнить деление
Z = ( 4 +- 3 i ) : ( -2 - 5 i )
Выполнить действия
Z = ( -1 + 3 i ) : ( 5 + i ) - ( 3 - 4 i ) : ( 4 + 3 i )
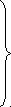

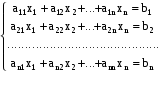 (1)
(1) , где
, где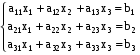 (2).
(2). и вычислим.
и вычислим.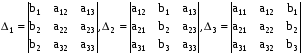 .
.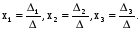
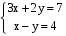
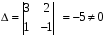

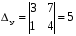
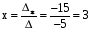
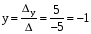 .
.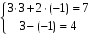 Ответ: ( 3 ; -1 ).
Ответ: ( 3 ; -1 ).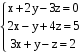
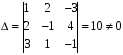
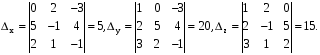
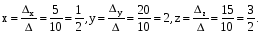
 Ответ: x=0,5; y=2; z=1,5 .
Ответ: x=0,5; y=2; z=1,5 .