|
Задания школьного тура математической олимпиады октябрь 2011, 9 класс
Задания школьного тура математической олимпиады
октябрь 2011, 9 класс
Придумайте такое нецелое число, что 15% и 33% от него – целые числа.
Туристам-байдарочникам нужны восемь одинаковых «сидушек» – мягких ковриков длиной не менее 35 см и шириной не менее 20 см. В спортивном магазине продаются большие коврики длиной 110 см и шириной 56 см. Хватит ли большого коврика на восемь «сидушек»?
Бумажный треугольник разрезали на два многоугольника прямолинейным разрезом, один из полученных многоугольников вновь разрезали на два и т. д. Какое наименьшее количество разрезов следует произвести, чтобы суммарное количество вершин у полученных многоугольников стало равно 400? Как это сделать?
У разбойников есть 13 слитков золота. Имеются весы, с помощью которых можно узнать суммарный вес любых двух слитков. Придумайте, как за 8 взвешиваний выяснить суммарный вес всех слитков.
У каждого трехзначного числа нашли произведение его цифр. Получилось 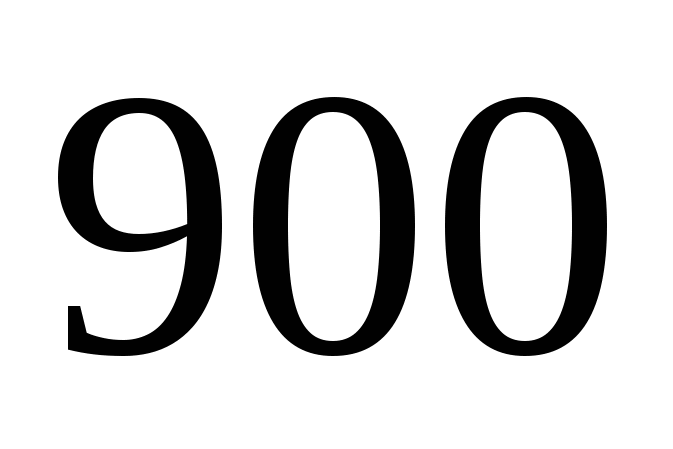 произведений от произведений от 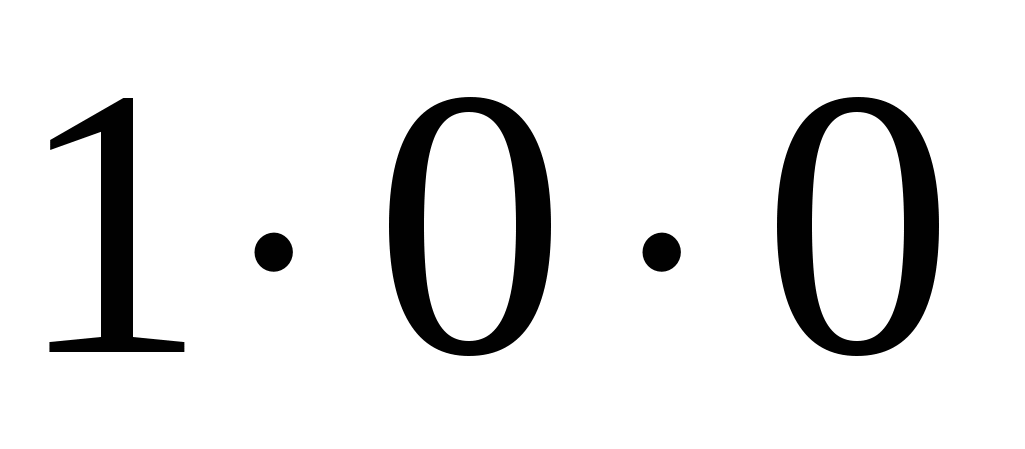 до до 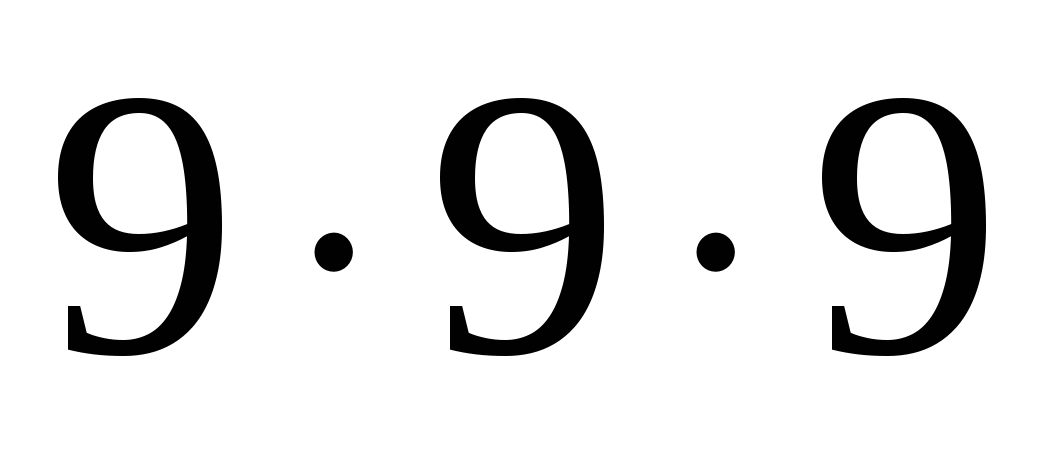 . Чему равна их сумма? . Чему равна их сумма?
Шестиугольник ABCDEF вписан в окружность. Докажите, что если AB||DE, AF||DC, то и BC||EF.
|
|
|
 Скачать 8.7 Kb.
Скачать 8.7 Kb.