|
Способы и методы, обеспечивающие реализацию требований к современному уроку. И. Н. Смирнова
Способы и методы, обеспечивающие реализацию требований к современному уроку.
И. Н. Смирнова
Концепция ФГОС, позиции системно-деятельностного и компетентностного подхода определяют систему требований к современному уроку. Вот некоторые из них:
Целеполагание. Перед обучающимися должны быть поставлены конкретные, достижимые, понятные цели. По возможности, целеполагание осуществляется совместно с обучающимися исходя из сформулированной, желательно – обучающимися, проблемы. Обучающиеся должны знать, какие конкретно знания и способы деятельности они освоят в процессе деятельности на уроке, и знать план достижения поставленных задач.
Мотивация. Учитель должен сформировать интерес, как самый действенный мотив, к процессу учебной деятельности и к достижению конечного результата.
Практическая значимость знаний и способов деятельности. Учитель должен показать обучающимся возможности применения получаемых знаний и умений в их практической деятельности.
Наличие блоков самостоятельного получения знаний обучающимися в процессе учебно-познавательной деятельности с помощью различных источников информации.
Организация групповой работы позволяет каждому ученику развивать коммуникативные компетенции и осваивать нормы работы в коллективе.
Использование системы самоконтроля и взаимоконтроля как средства формирования ответственности за результаты своей деятельности.
Рефлексия как осознание себя в процессе деятельности.
Выполнение данных требований определяет роль учителя как управленца, а обучающихся – как активных субъектов деятельности, что становится решающими предпосылками реализации целевых установок Стандарта.
Я хочу поделиться опытом в реализации некоторых из этих требований.
Некоторые приемы целеполагания.
Тема-вопрос. Тема урока формулируется в виде вопроса. Учащимся необходимо построить план действий, чтобы ответить на поставленный вопрос. Дети выдвигают множество мнений, чем больше мнений, тем лучше развито умение слушать друг друга и поддерживать идеи других.
Например, для темы урока “Что мы знаем об умножении?” учащиеся построили план действий:
Что значит умножить одно число на другое (повторить связь сложения и умножения).
Повторить названия компонентов при умножении.
Повторить таблицу умножения.
Повторить правила умножения в столбик.
Повторить свойства нуля и единицы при умножении.
Как сделать проверку при умножении.
Домысливание. Предлагается тема урока и слова “помощники”:
Узнать…, Научиться…, Повторить…, Приобрести навык…, Поразмыслить…, Задуматься о …, Сделать…. С помощью слов “помощников” дети формулируют цели урока. Определить причину объединения слов, предметов, фигур, проводя анализ закономерности и опираясь на свои знания. Например, для урока по теме “Порядок действий в выражениях со скобками и без скобок” предлагается несколько выражений, записанных в два столбика (слева выражения без скобок, а справа – со скобками). Задаются вопросы: “Что объединяет выражения слева? справа? Как провести вычисления? Что для этого надо знать?” затем учащимися формулируется тема и цели урока.
Ситуация противоречия между известным и неизвестным. Создается ситуация противоречия между известным и неизвестным. Последовательность применения данного приема такова:
Самостоятельное решение.
Коллективная проверка результатов.
Выявление причин разногласий результатов или затруднений выполнения.
Постановка целей урока.
Например, вначале урока по теме “Связь сложения и вычитания” проводится математический цифровой диктант. Учитель произносит некоторое утверждение и, если ученик согласен, то он ставит 1, если нет – 0.
Результат сложения называют суммой.
Число не изменится, если к нему прибавить 0.
Если от числа отнять 0, оно увеличится.
Если из суммы двух чисел вычесть одно из них, то получится другое число.
Если к разности прибавить уменьшаемое, то получится вычитаемое.
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Разность показывает, на сколько единиц одно число больше или меньше другого.
Если одно из слагаемых уменьшить на 20, а другое оставить без изменения, то и сумма уменьшится на 20.
При сложении ответ всегда больше первого слагаемого.
Затем проводится самопроверка по образцу, который выводится на доску. Учащиеся анализируют вопросы диктанта, свои результаты и затем, в результате коллективного обсуждения, формулируют тему и цели урока.
Некоторые приемы мотивации.
Цели этапа мотивации: раскрыть значимость изучения нового материала, привлечь внимание учащихся, пробудить их интерес, желание понять, применить. Каким же способом можно заинтересовать учащихся?
Можно использовать следующий материал:
Исторические задачи, легенды, сведения из истории по данной теме.
Решение задач с практическим содержанием, с использованием межпредметных связей.
Проведение исследовательских, лабораторных и практических работ с использованием моделей, чертежей, таблиц и т.п.
Решение задач, требующих расширение знаний по теме.
Математические фокусы, задачи занимательного характера.
Формируя мотивацию обучения, я использую следующие приемы.
Урок без темы. В начале урока тема не объявляется. После того как ребята получили стимул, тема изучается, формируются первые навыки. После этого надо обязательно вернуться к заданию, с которого начиналось изучение темы, и дать возможность ребятам решить задание повторно.
Тема “Деление дробей”. Наряду с другими заданиями устного счета, дается задание решить задачу: “Длина прямоугольника  , ширина прямоугольника , ширина прямоугольника 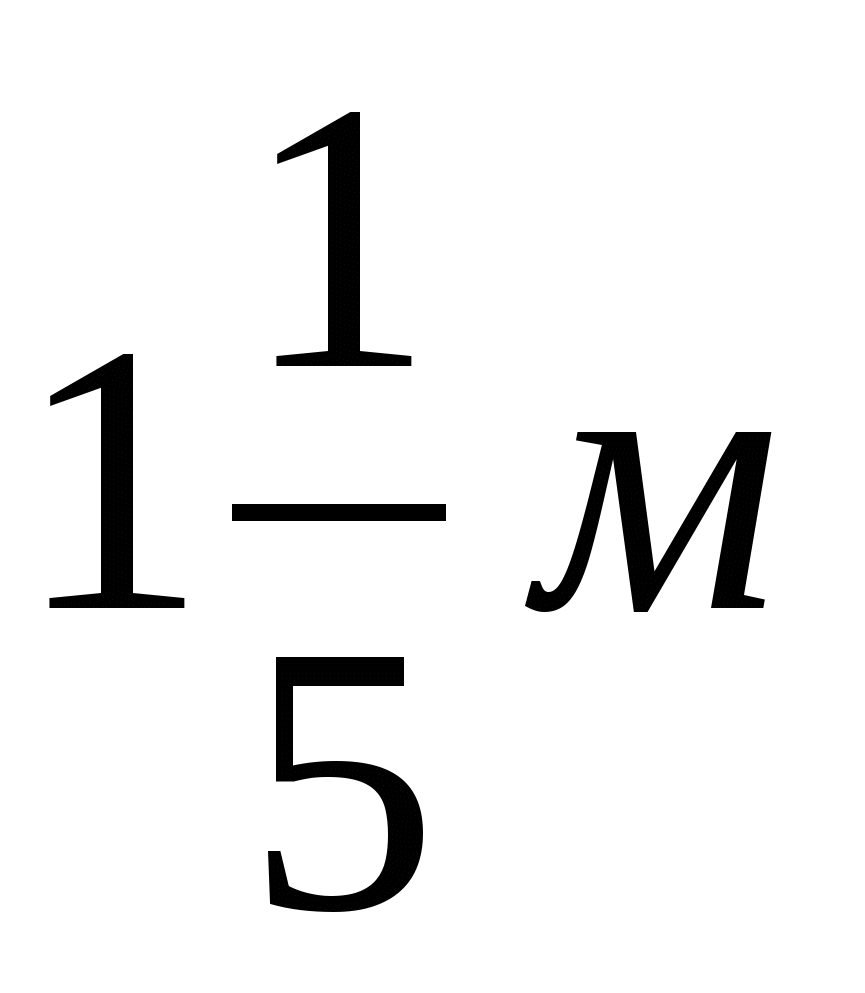 . Найдите площадь прямоугольника”. И тут же после решения задачи следующее задание: “Составьте задачу, обратную данной”. Ребята составляют несколько вариантов, один из которых решают и попадают в тупик. Не умеют они делить дроби. Озадачили их? Продолжаем урок: “Так что же мы должны научиться делать сегодня на уроке?” И обучающиеся сами определяют цели урока: “Сегодня мы должны научиться делить дроби”, формулируют тему урока. . Найдите площадь прямоугольника”. И тут же после решения задачи следующее задание: “Составьте задачу, обратную данной”. Ребята составляют несколько вариантов, один из которых решают и попадают в тупик. Не умеют они делить дроби. Озадачили их? Продолжаем урок: “Так что же мы должны научиться делать сегодня на уроке?” И обучающиеся сами определяют цели урока: “Сегодня мы должны научиться делить дроби”, формулируют тему урока.
Исторические задачи. Тема урока “Рациональные вычисления”. Детям предлагается решить “задачу маленького Гаусса” – найти сумму всех натуральных чисел от 1 до 100. Даю некоторое время на вычисления. Заслушиваем результаты ребят и способ вычисления. Если рационального способа нет, то объявляется тема урока.
Ситуация удивления. Урок по теме “Признаки делимости” начинается так “А знаете ребята, я могу назвать себя мудрецом. Я могу мгновенно ответить вам, делится ли число на 2, 3, 4, 5, 6, 9, 10, не выполняя деления в столбик или на калькуляторе. Хотите проверить? Напишите у себя число и определите делится ли оно на какое-нибудь из названных чисел”. Ребята начинают отыскивать мне числа. Они удивлены моим угадыванием. “А хотите, я вас научу? Мы приступаем к новой теме, которая поможет вам стать такими же мудрецами. Она называется “Признаки делимости””.
Приемы самоконтроля. Проведение самоконтроля направлено на осознание правильности своих действий, на предупреждение или обнаружение уже совершенных ошибок. Процесс формирования самоконтроля можно представить в виде схемы.
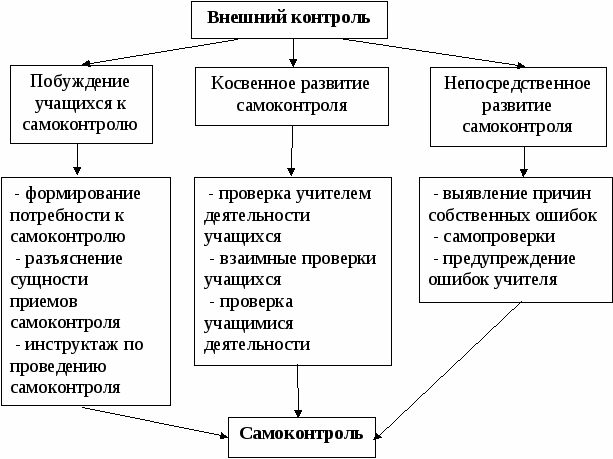
При обучении самоконтролю я уделяю особое внимание ознакомлению и овладению учащимися приемами проведения контролирующих действий. Определенные трудности здесь связаны с тем, что в процессе преподавания математики используется большое число таких приемов. Вот некоторые приемы самоконтроля:
сверка с образцом (ответом);
решение задачи разными способами;
решение обратной задачи;
проверка полученных результатов по условию задачи;
примерная оценка искомых результатов;
проверка на частном случае.
Некоторые приемы рефлексии. Используя рефлексию, учитель имеет возможность отслеживать в процессе урока уровень понимания учениками учебного материала, особенности их психологического состояния, отношение к изучаемому материалу и уроку в целом с помощью обратной связи. Исходя из того, что рефлексия по форме бывает вербальной (устной и письменной), образной (цвет, рисунок, символ), можно использовать множество приемов. Вот некоторые из них.
Рефлексия правил. Тема “Сложение и вычитание дробей”.
|
Знаю правило
|
Понимаю правило
|
Умею применять
правило
|
Смогу применить правило самостоятельно
|
Я … складывать дроби.
|
|
|
|
|
Я … вычитать дроби.
|
|
|
|
|
Рефлексия деятельности. Учащимся дается карточка, в которой надо подчеркнуть фразы, характеризующие работу ученика на уроке по трем направлениям.
Урок
|
Я на уроке
|
Итог
|
Интересно
|
Работал
|
Понял материал
|
Скучно
|
Отдыхал
|
Узнал больше, чем знал
|
Безразлично
|
Помогал другим
|
Не понял
|
Рефлексия “Ценности урока (или проделанной работы)”.
Получение новой информации
|
|
Процесс личной деятельности
|
|
Полученный результат
|
|
Деловое общение во время работы
|
|
Возможность проявить себя и услышать слова одобрения
|
|
Получение оценки
|
|
1 – самое важное, 2 – важное, 3 – не очень важное, 4 – совсем не важное
Библиографический список
Методика организации целеполагания учащихся на уроке. Материалы дистанционного курса. [Электронный ресурс]. Версия 1.0 / Сост. Хуторской А.В., Кулешова Г.М. - М.: Центр дистанционного образования "Эйдос", 2007.- 390 Кб
Как организовать рефлексию учащихся. Материалы дистанционного курса. [Электронный ресурс]. Версия 1.0 / Сост. Хуторской А.В. - М.: Центр дистанционного образования "Эйдос", 2006.- 290 Кб
Манвелов С. Современный урок математики: основы методики проведения. Газета “Математика”, № 41/98.
Семушкин А. Д., Кретинин О. С., Семенов Е.Е. Активизация мыслительной деятельности учащихся при изучении математики.- М., 1978.
Каким должен быть современный урок. https://it-n.ru.
|
|
|
 Скачать 75.86 Kb.
Скачать 75.86 Kb.