|
Решение уравнений, неравенств и систем с помощью графических образов на плоскости. Для внесения ответов к тестовым задачам
Фамилия______________________________________Оценка__________________.
10 задач для зачета по теме:” Решение уравнений, неравенств и систем с помощью графических образов на плоскости”.
Для внесения ответов к тестовым задачам:
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
4
|
4
|
4
|
4
|
4
|
4
|
4
|
4
|
4
|
4
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
1. Сколько различных корней имеет уравнение 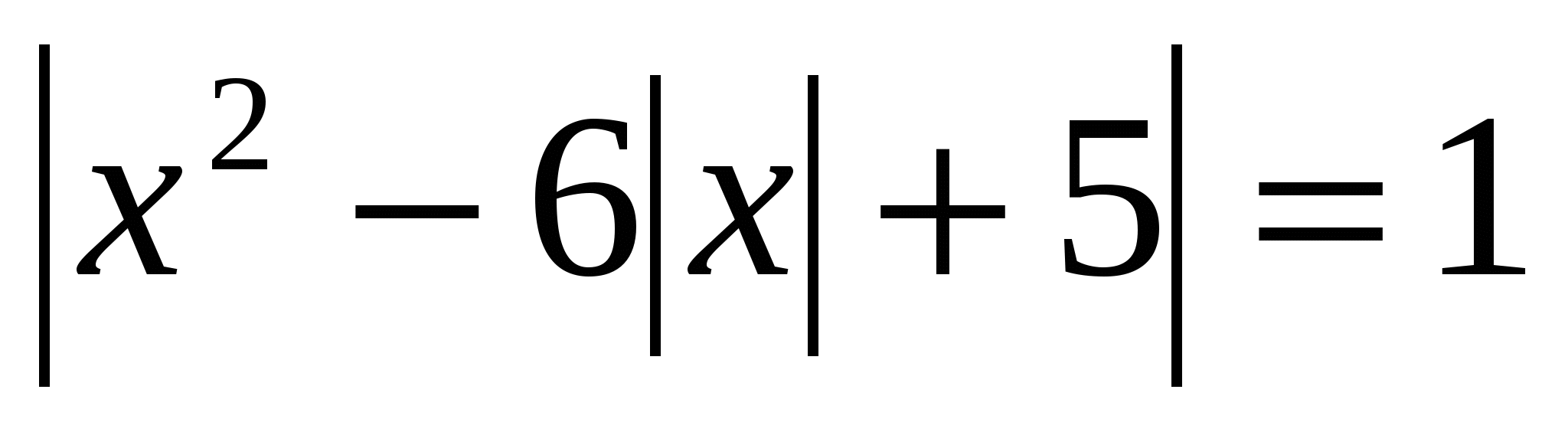 ? ?
1
|
2
|
3
|
4
|
5
|
три
|
четыре
|
корней нет
|
шесть
|
восемь
|
Сколько имеется различных целых значений параметра p, при которых уравнение 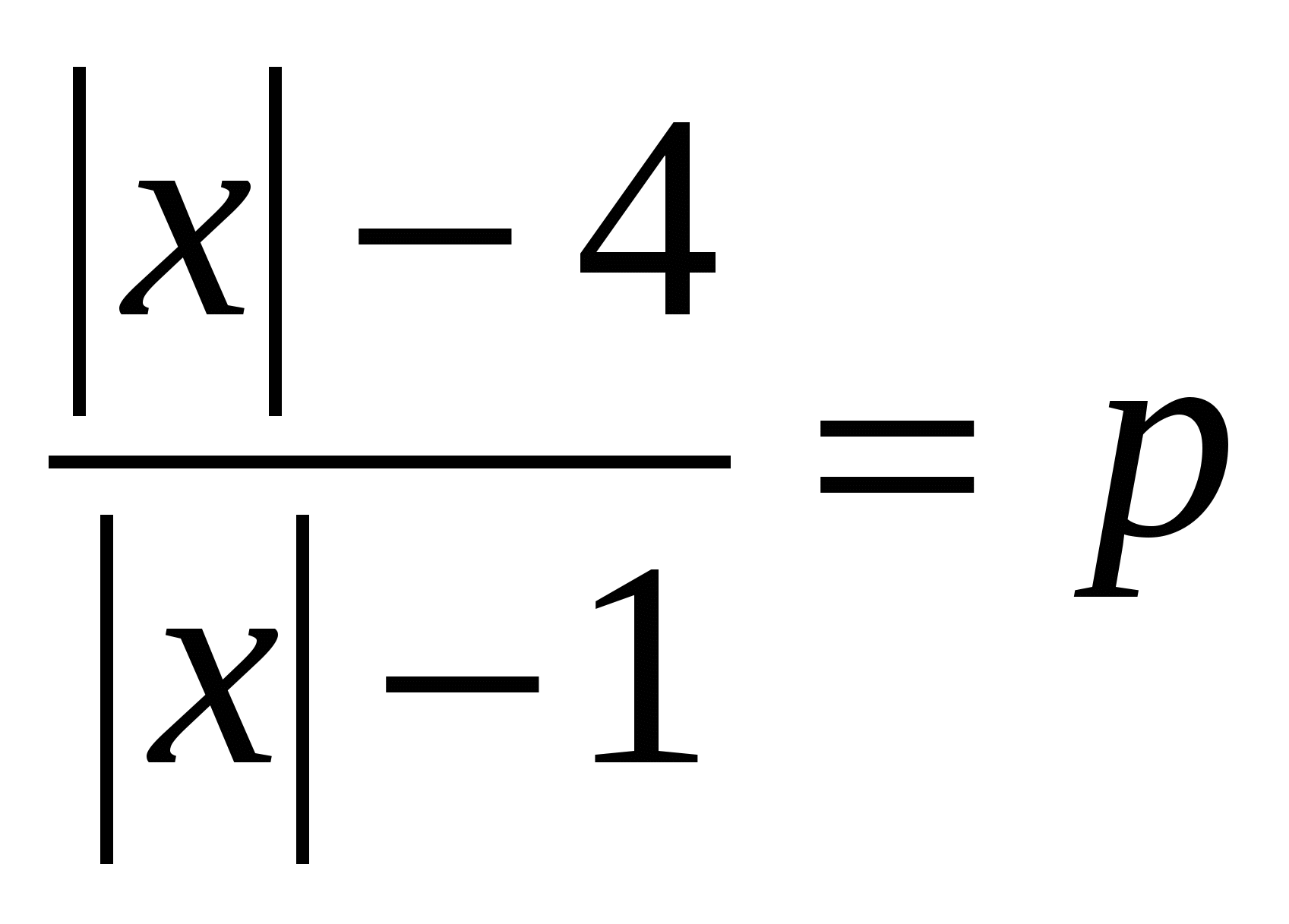 не имеет корней? не имеет корней?
1
|
2
|
3
|
4
|
5
|
ни одного или одно
|
два
|
три
|
четыре
|
пять или больше пяти
|
3. Пусть N- количество различных целочисленных значений параметра p, при которых система 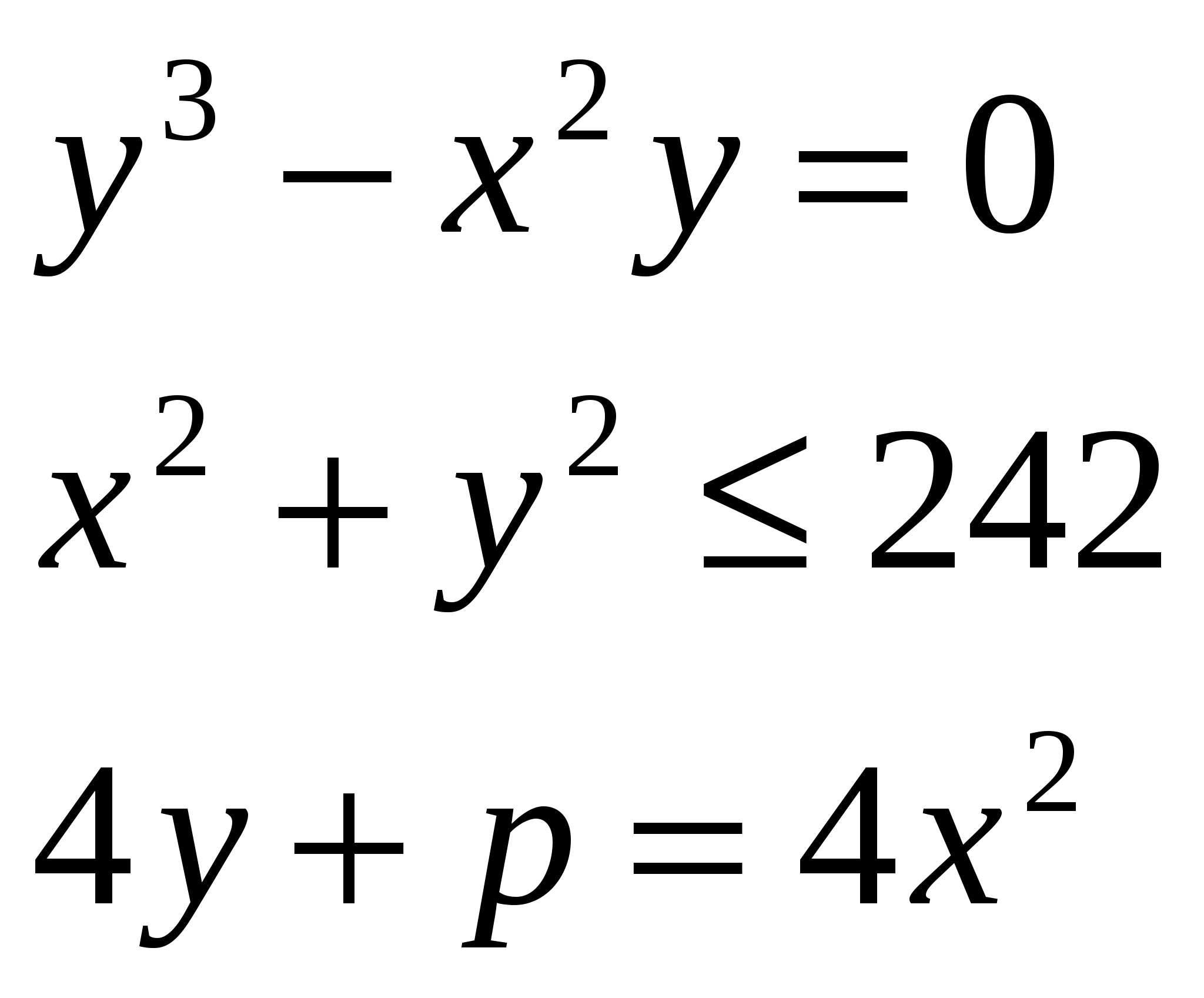 имеет ровно два различных решения? Остаток от деления на 5 равен имеет ровно два различных решения? Остаток от деления на 5 равен
4. Сколько имеется целых положительных значений параметра p, при которых система уравнений 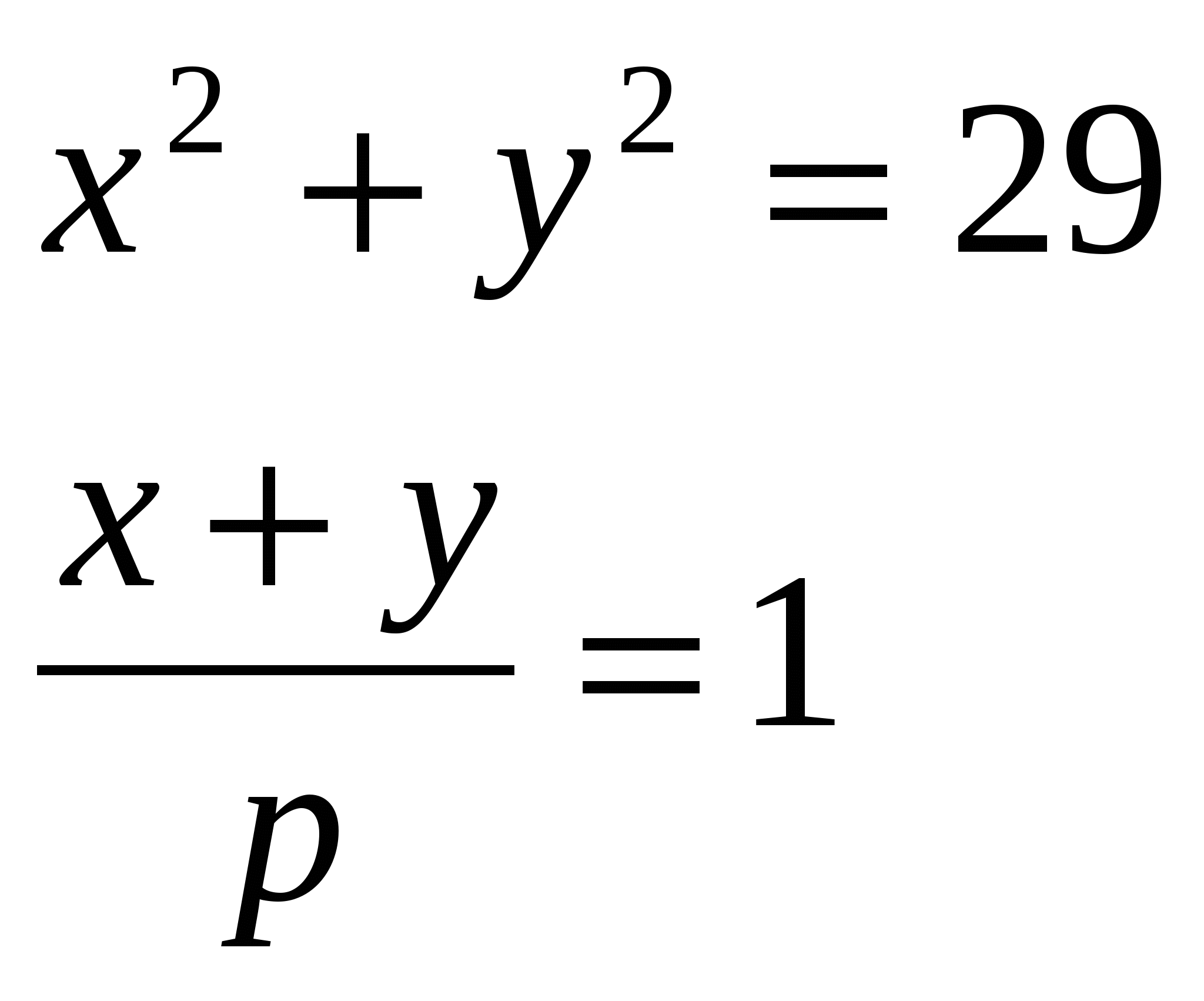 имеет ровно два различных решения? имеет ровно два различных решения?
1
|
2
|
3
|
4
|
5
|
меньше шести
|
шесть
|
семь
|
восемь
|
больше восьми
|
5. Все значения параметра p, при которых система уравнений 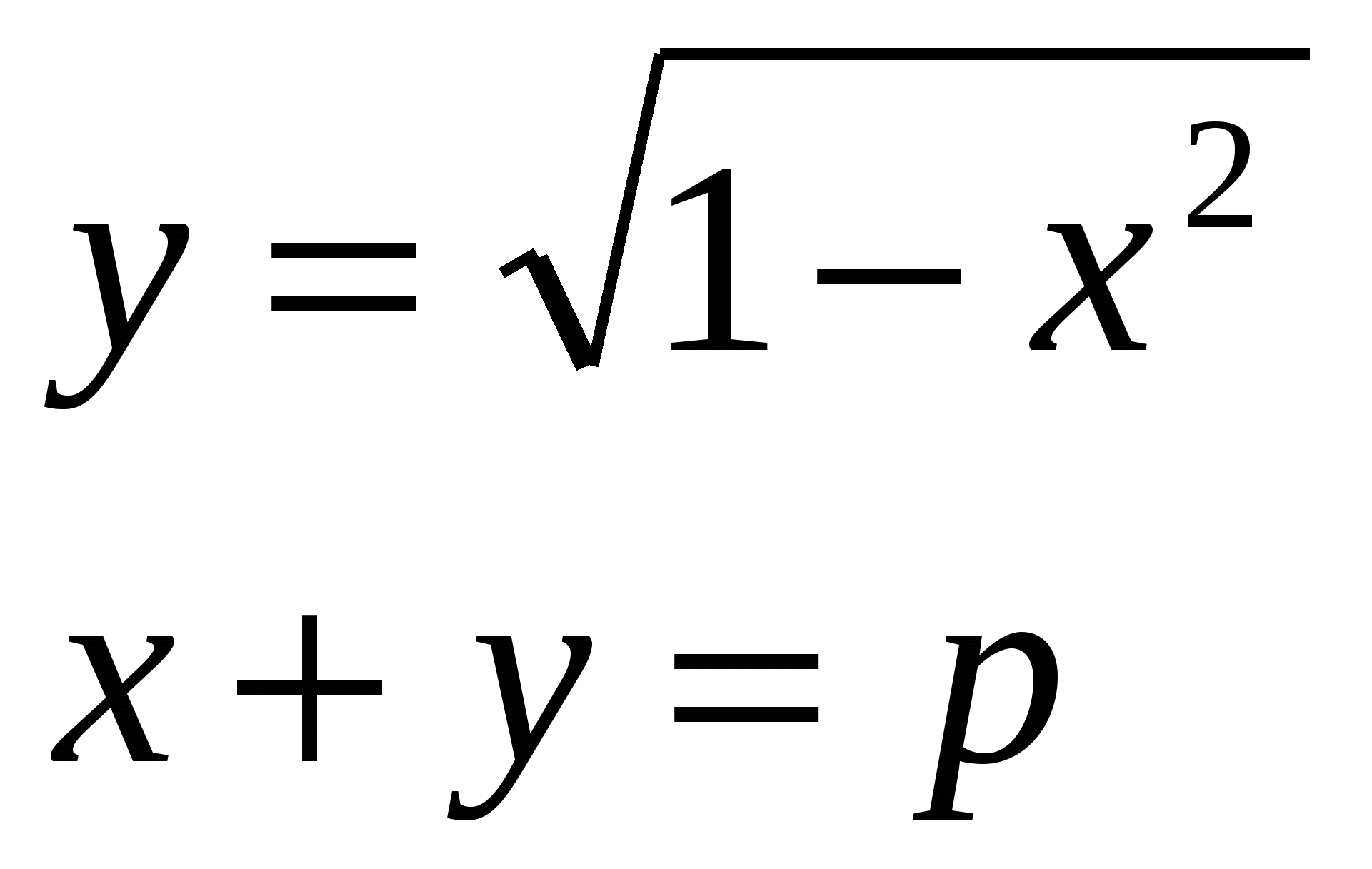 имеет ровно два различных решения, образуют промежуток, длина которого равна имеет ровно два различных решения, образуют промежуток, длина которого равна
6. Сумма двух наибольших значений параметра p, при которых система уравнений 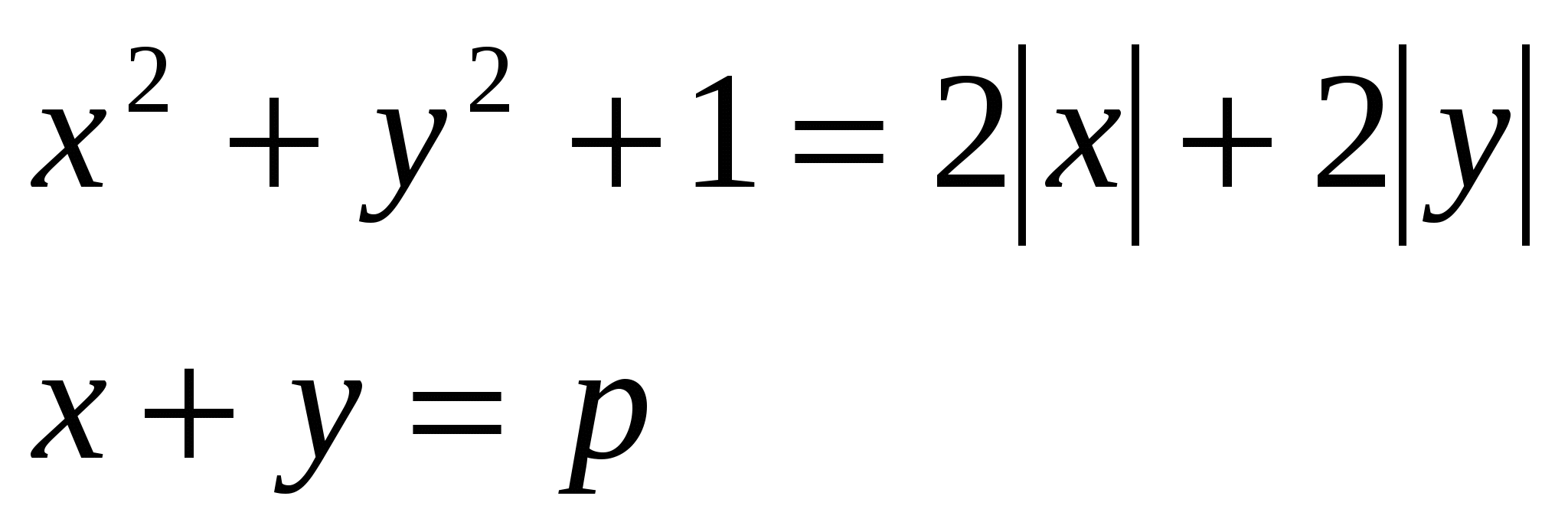 имеет ровно четыре решения, равна имеет ровно четыре решения, равна
7. Множество всех значений параметра p, при которых хотя бы одно число 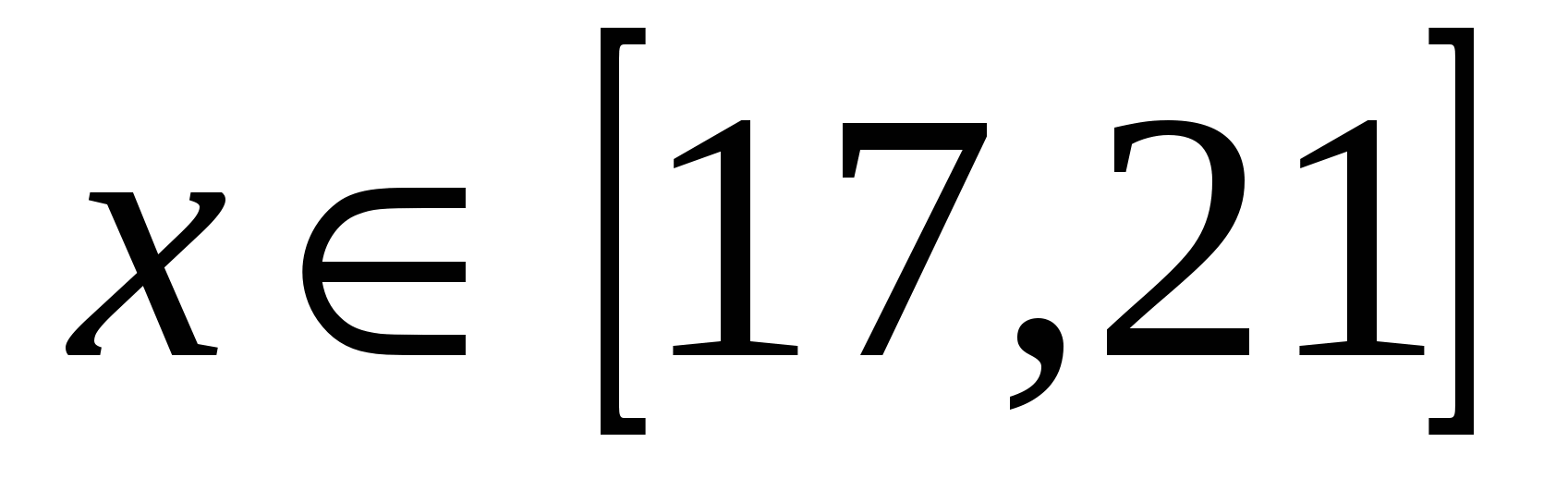 является решением неравенства является решением неравенства 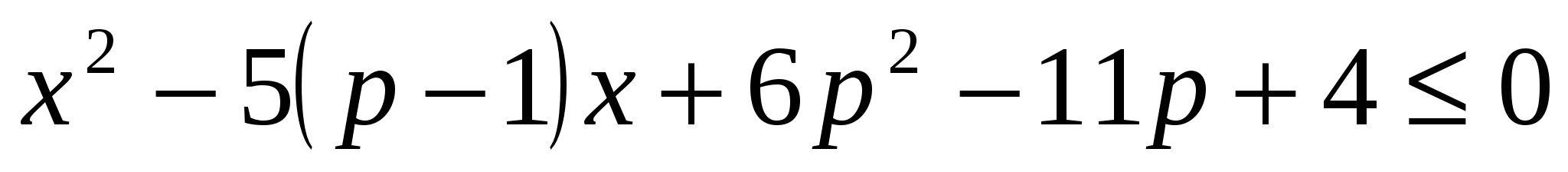 , является промежутком, длина которого равна L. Укажите верное утверждение , является промежутком, длина которого равна L. Укажите верное утверждение
8. Сумма всех различных целочисленных значений параметра  , при которых система неравенств , при которых система неравенств 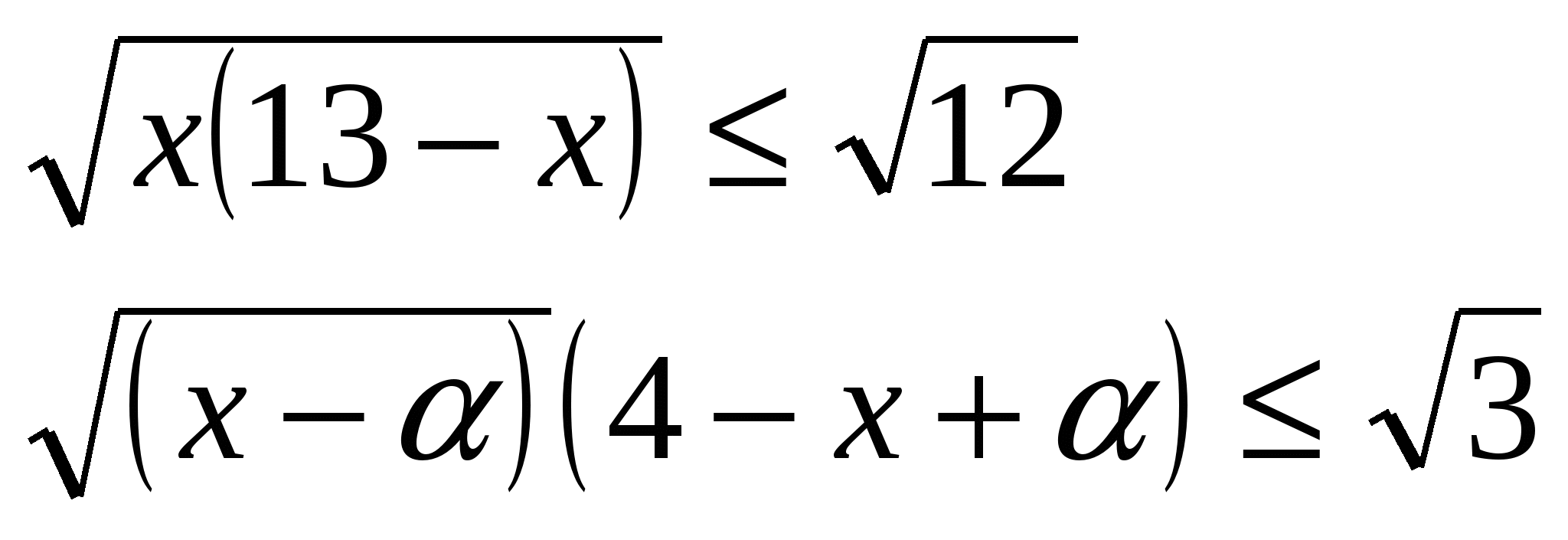 имеет единственное решение, равна натуральному числу. Укажите остаток от деления этого натурального числа на 5. имеет единственное решение, равна натуральному числу. Укажите остаток от деления этого натурального числа на 5.
9. Если значение параметра p таково, что p>0 и уравнение 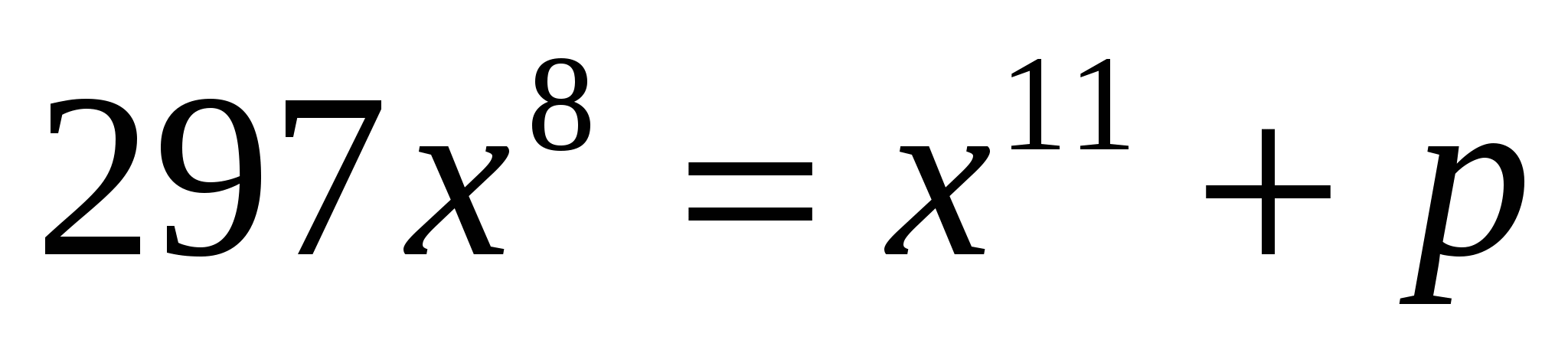 имеет ровно два различных корня, то p- натуральное число, остаток от деления которого на 5 равен имеет ровно два различных корня, то p- натуральное число, остаток от деления которого на 5 равен
10. Сколько существует различных натуральных значений параметра b, при которых система уравнений 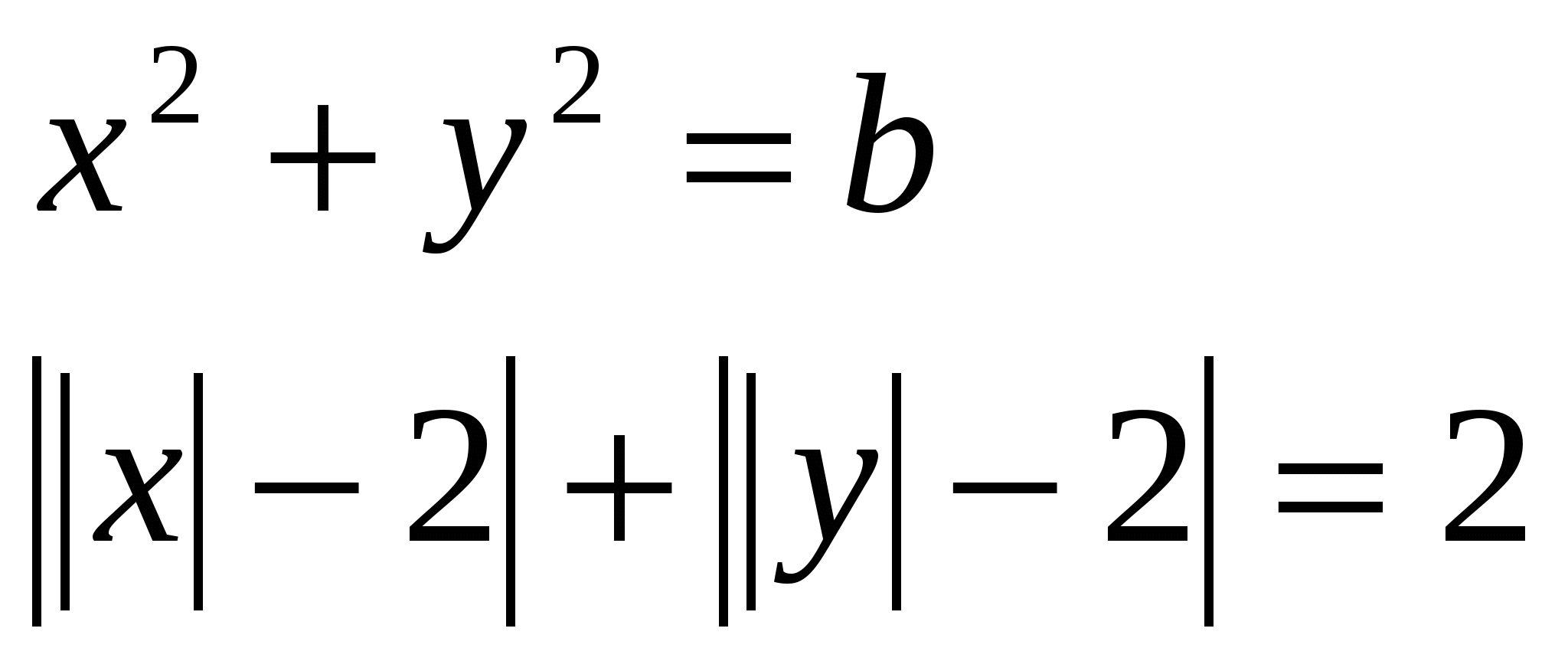 имеет ровно восемь различных решений? Укажите остаток от деления этого числа на 5. имеет ровно восемь различных решений? Укажите остаток от деления этого числа на 5.
15. Наименьшее значение функции 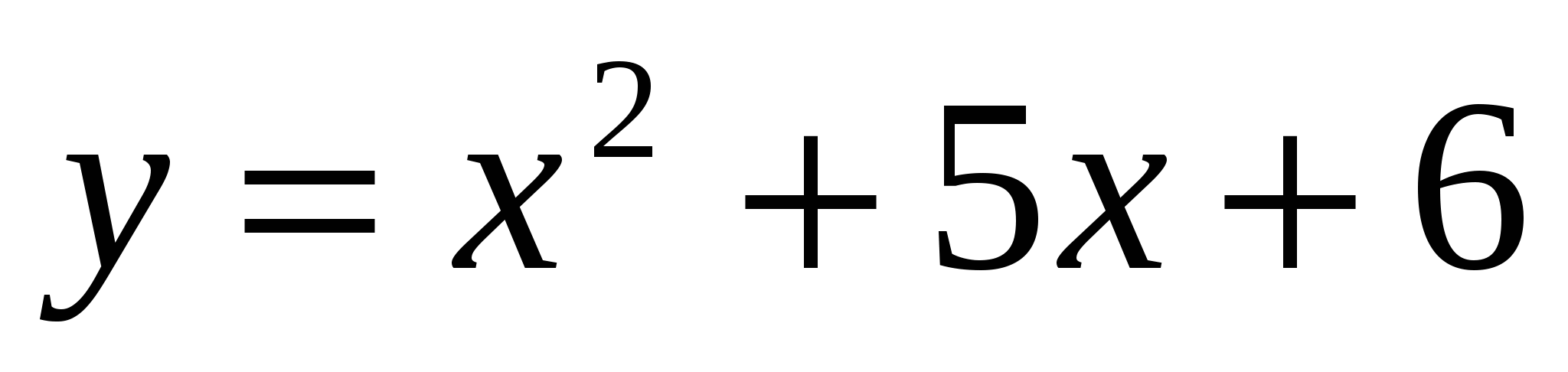 равно равно
1
|
2
|
3
|
4
|
5
|
-3,75
|
0,75
|
-0,75
|
0,25
|
-0,25
|
16. Парабола 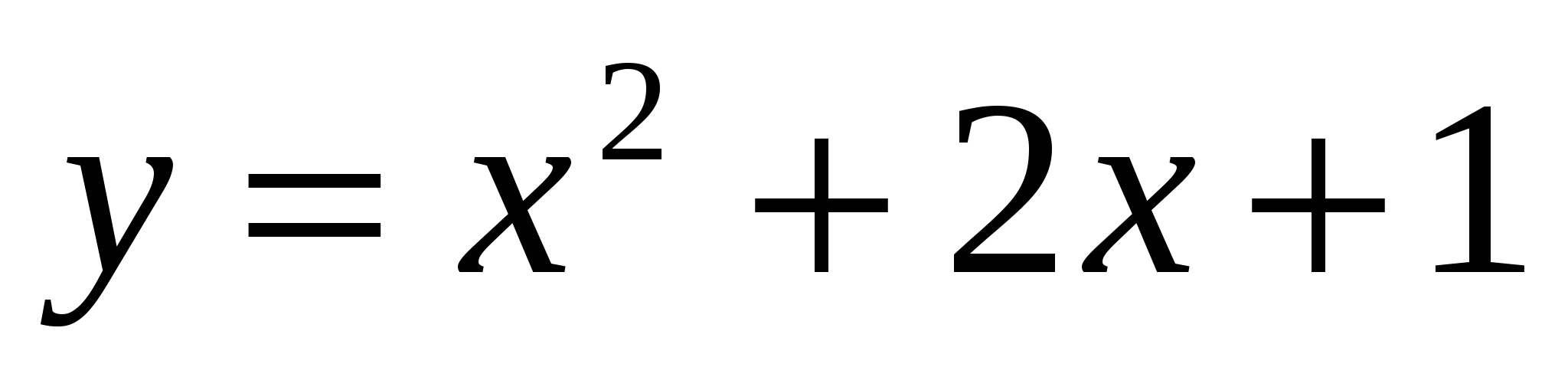 и прямая и прямая 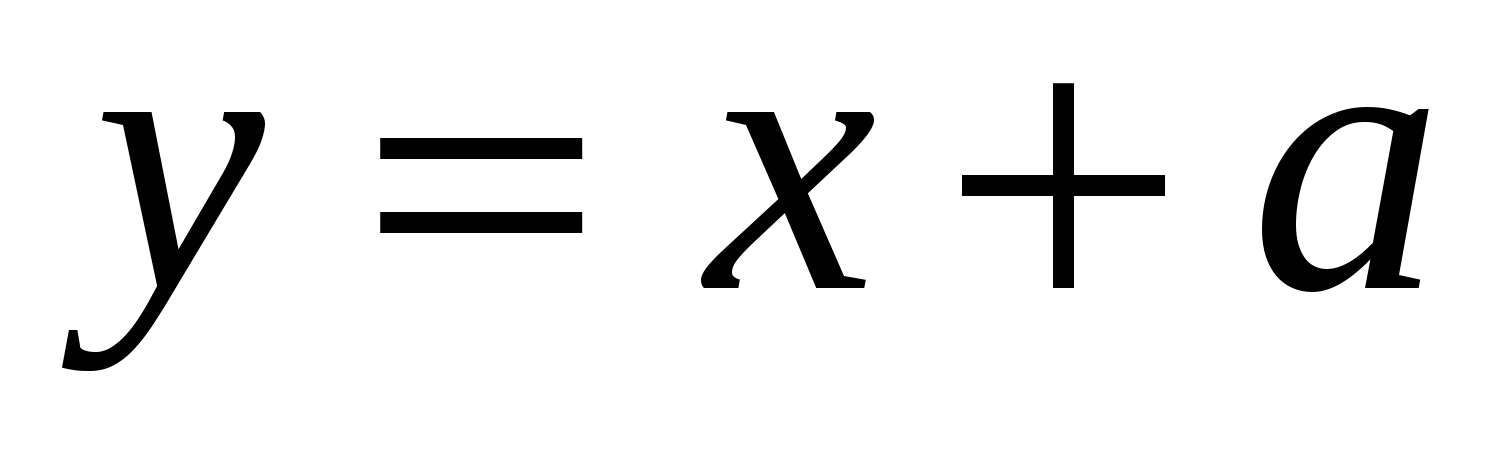 касаются, если касаются, если
1
|
2
|
3
|
4
|
5
|
а = - 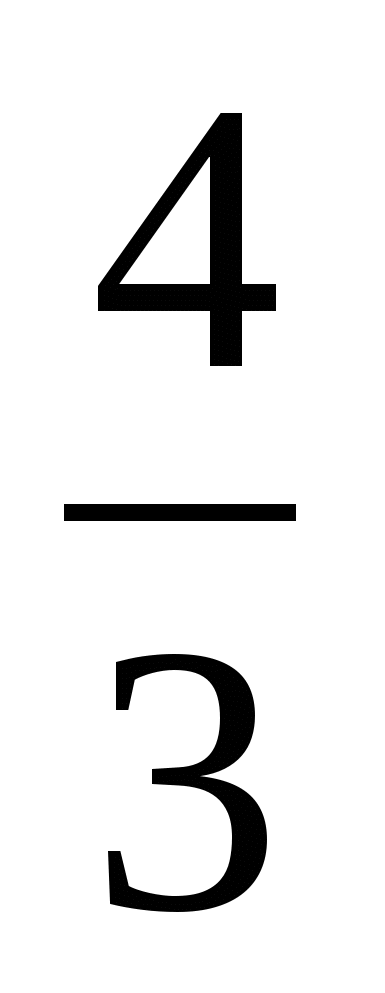
|
а = 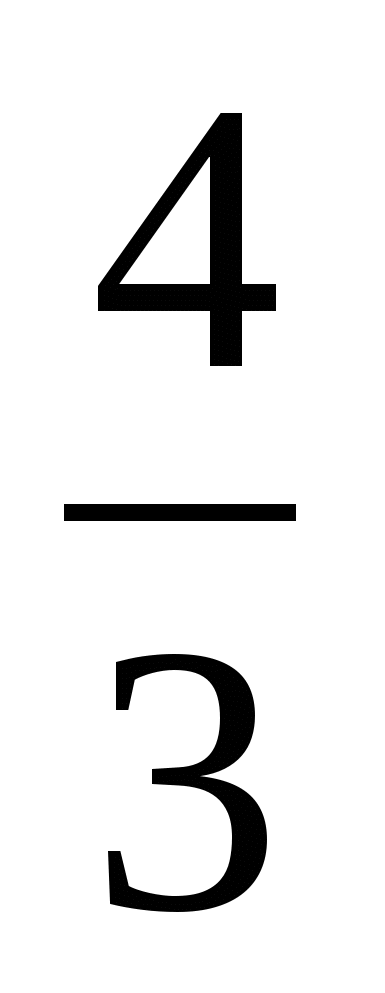
|
а = 1
|
а = 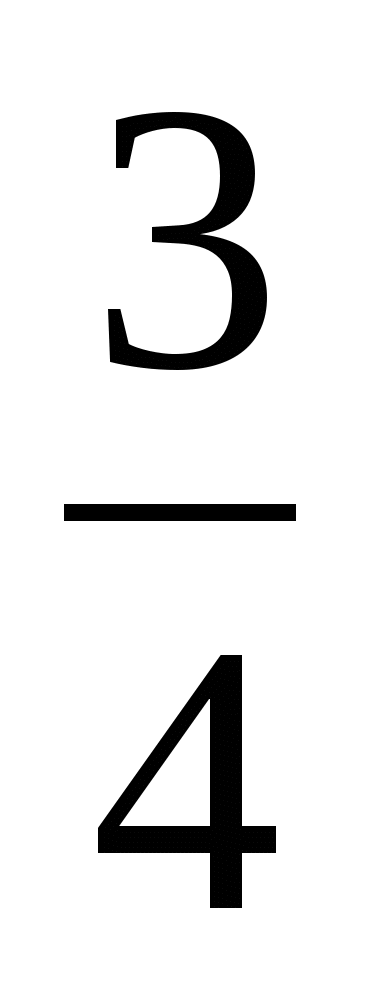
|
а = 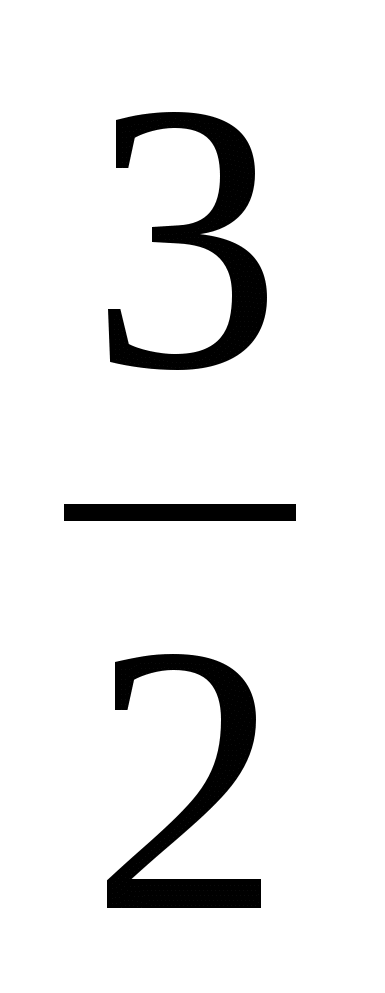
|
17. Произведение всех корней уравнения 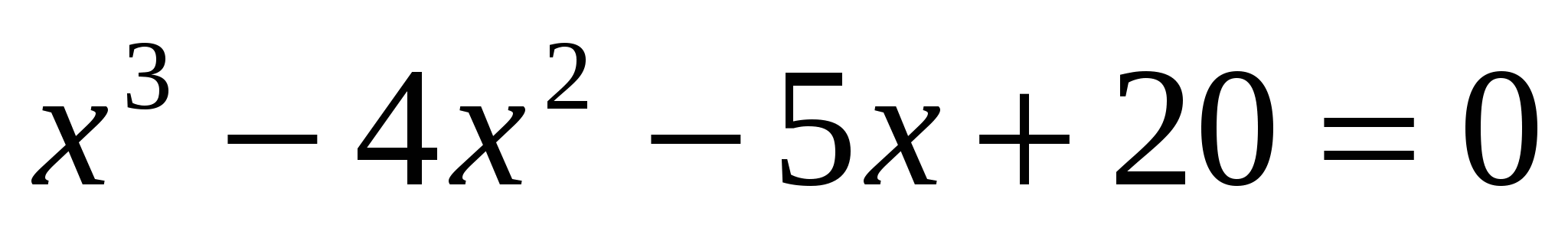 равно равно
1
|
2
|
3
|
4
|
5
|
20
|
-20
|
10
|
-10
|
25
|
18. Разность между наименьшим положительным и наименьшим отрицательным корнями уравнения 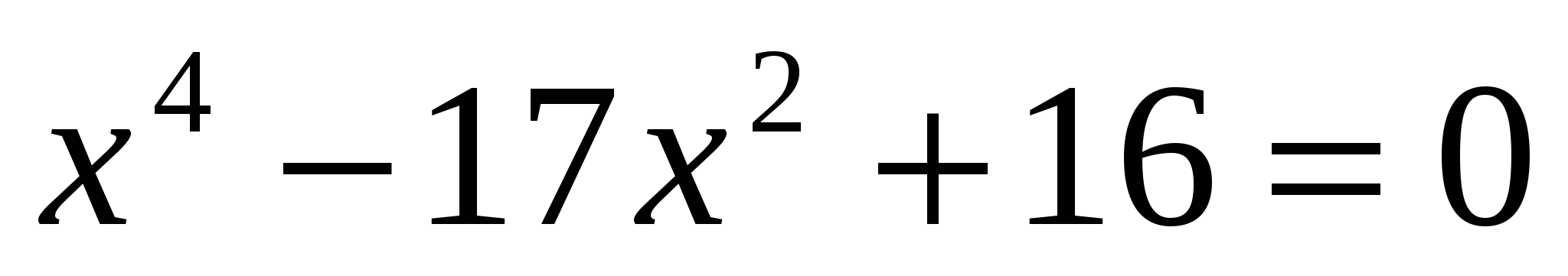 равна равна
19. Найти остаток от деления на 5 числа П, если П – произведение всех различных корней уравнения 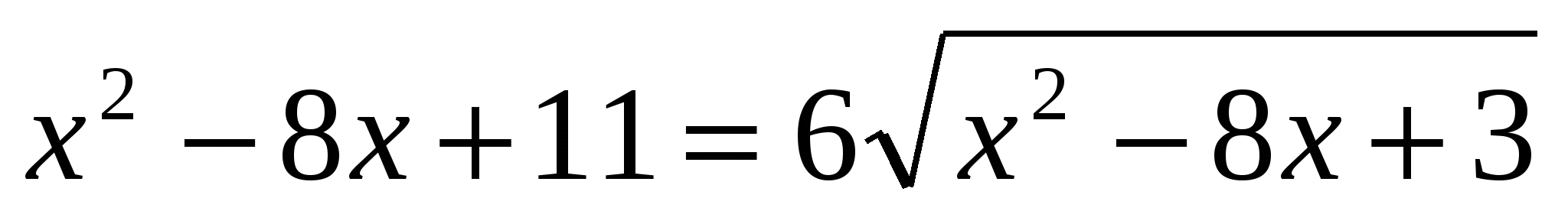 . .
20. Значение cos 300 равно
21. Найти tg, если 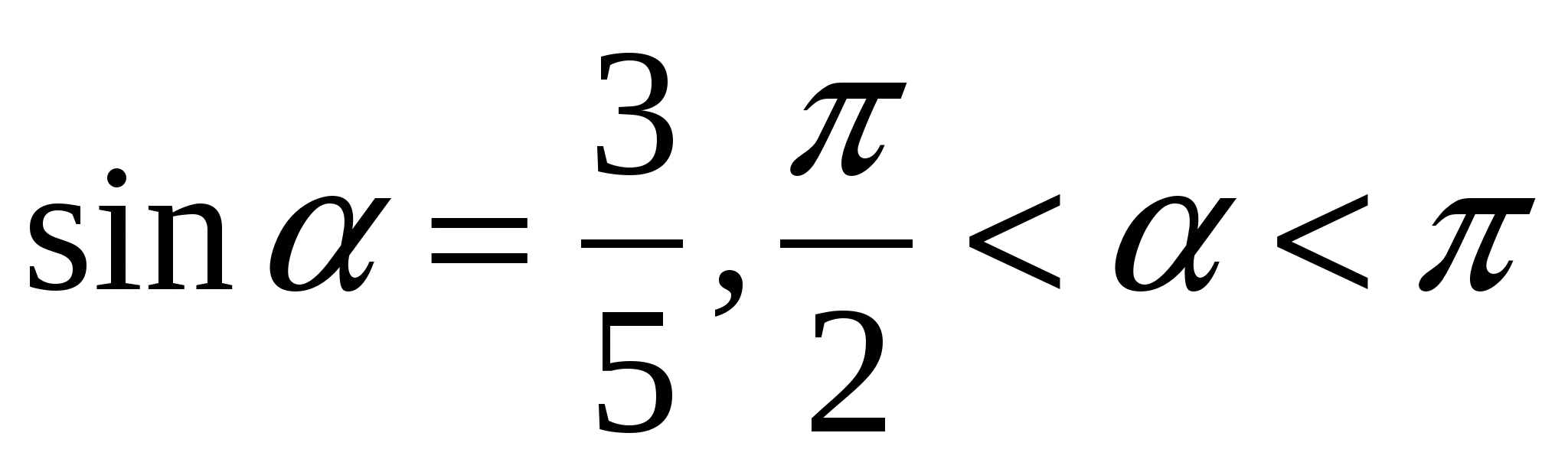 : :
1
|
2
|
3
|
4
|
5
|
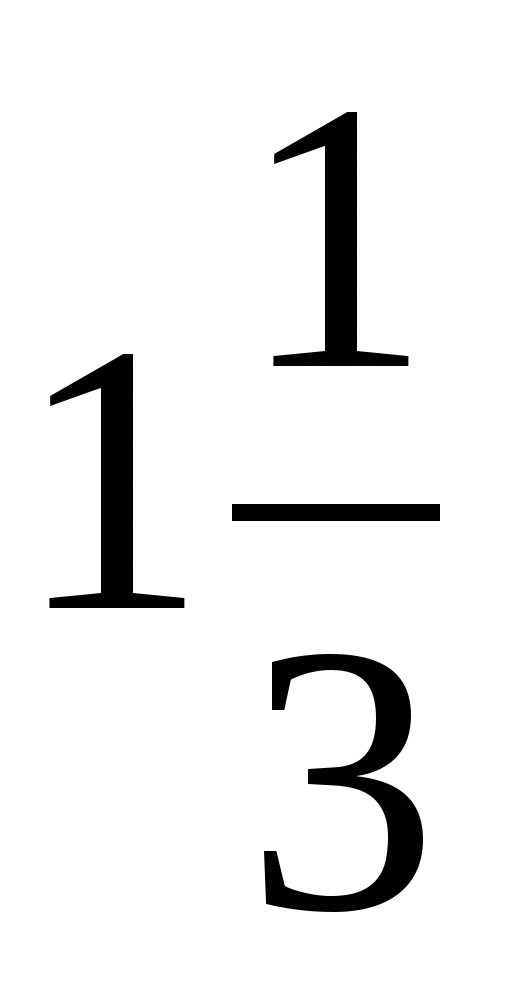
|
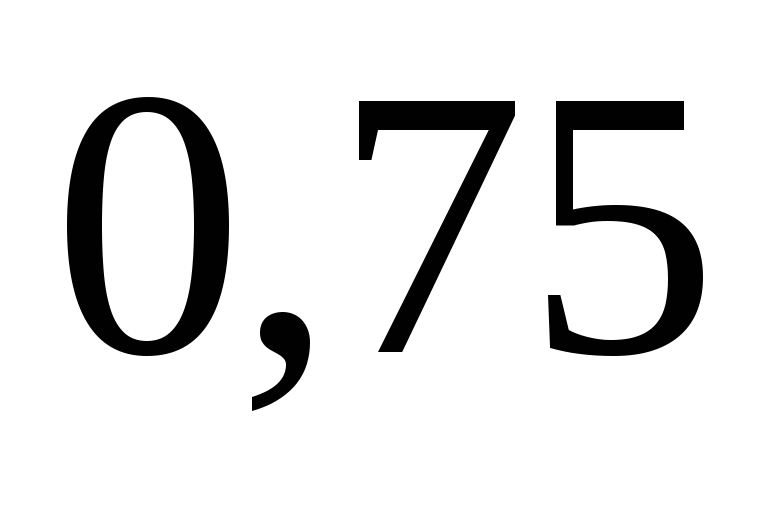
|
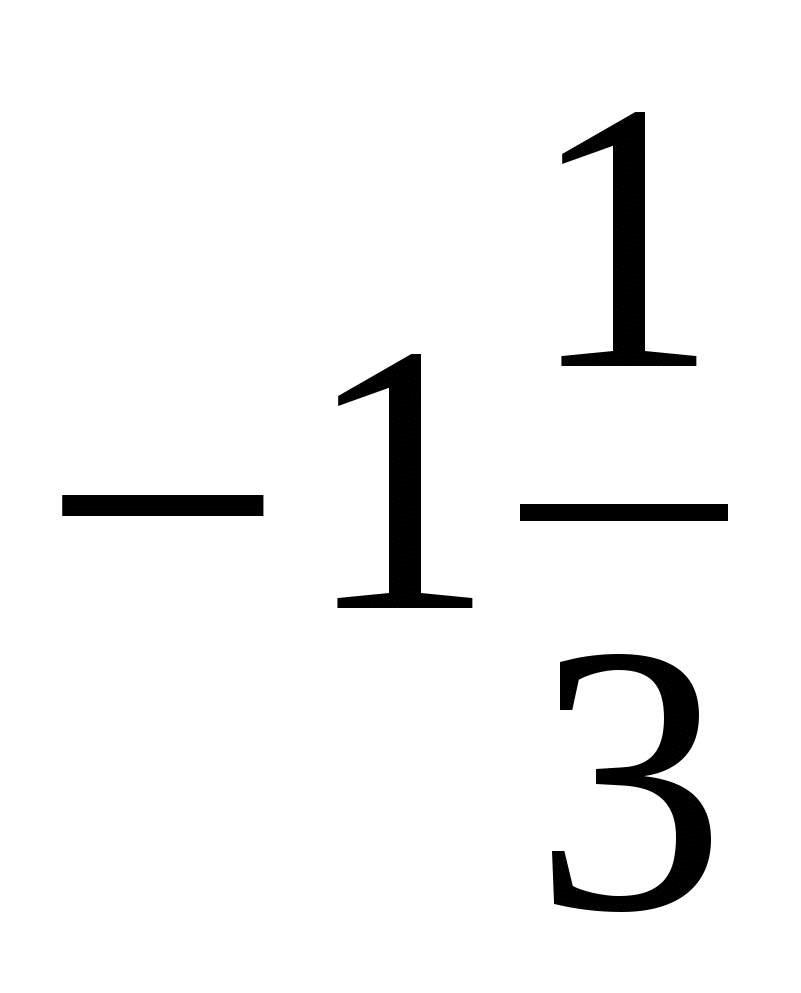
|
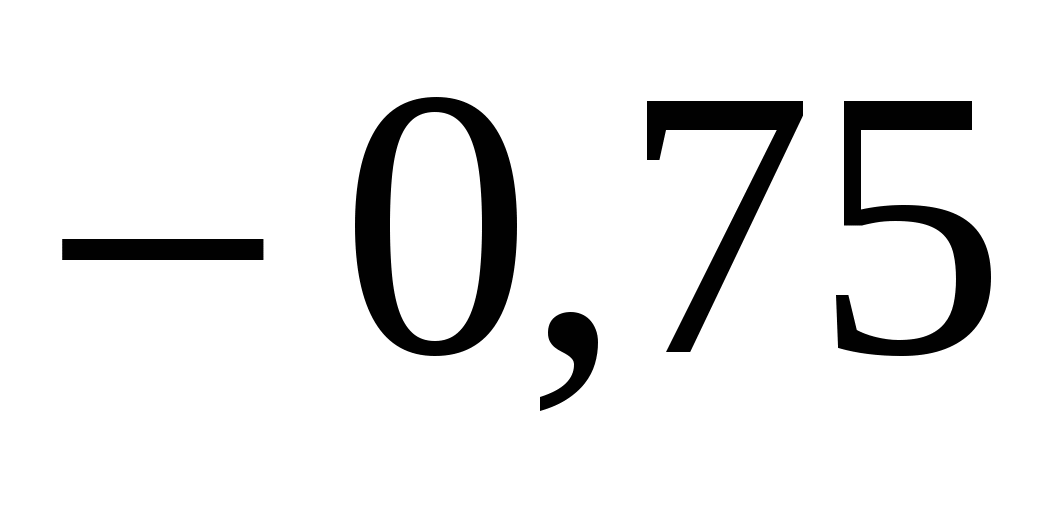
|
среди ответов 1-4 нет правильного
|
22. Множество значений функции 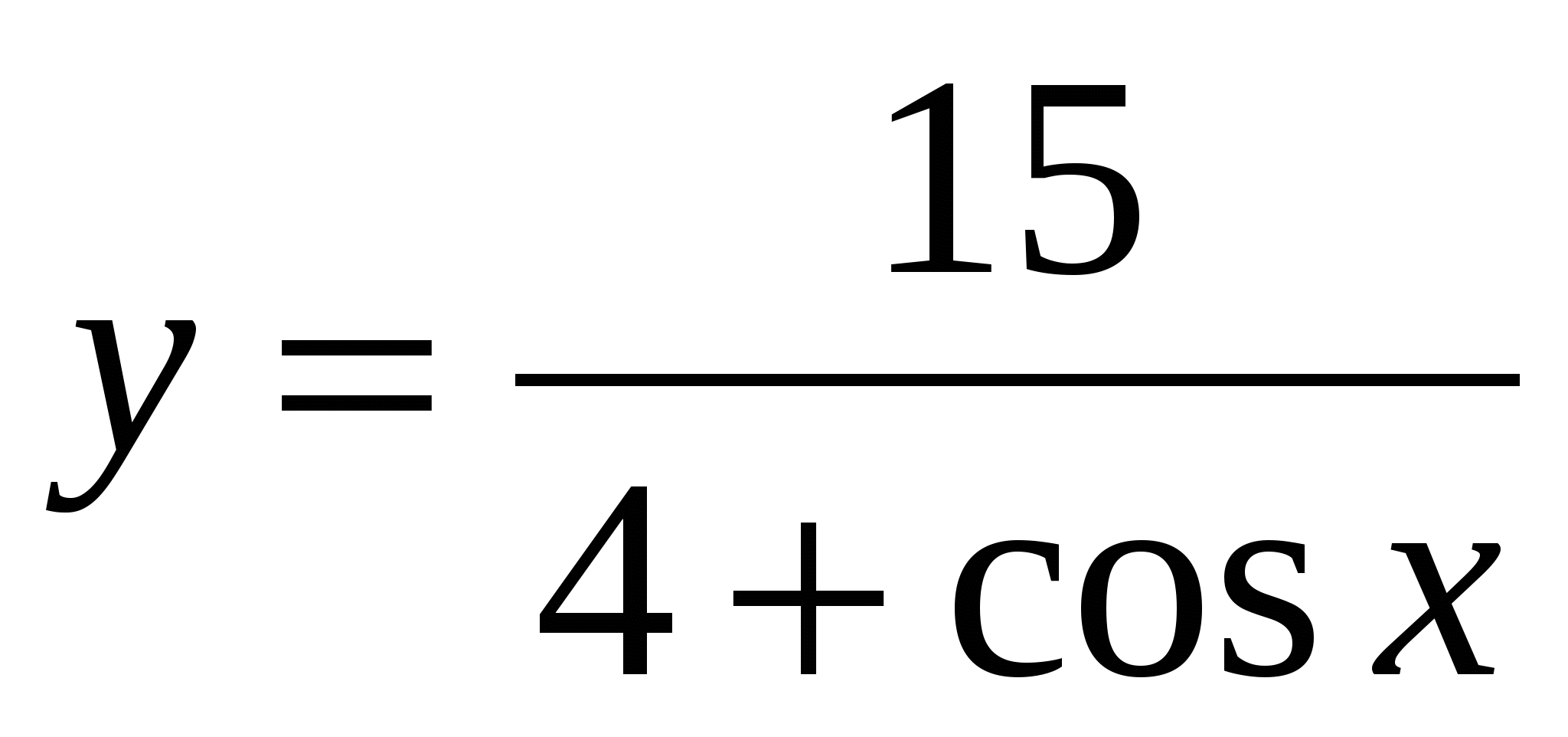 представляет собой отрезок, длина которого равна представляет собой отрезок, длина которого равна
23. Найти 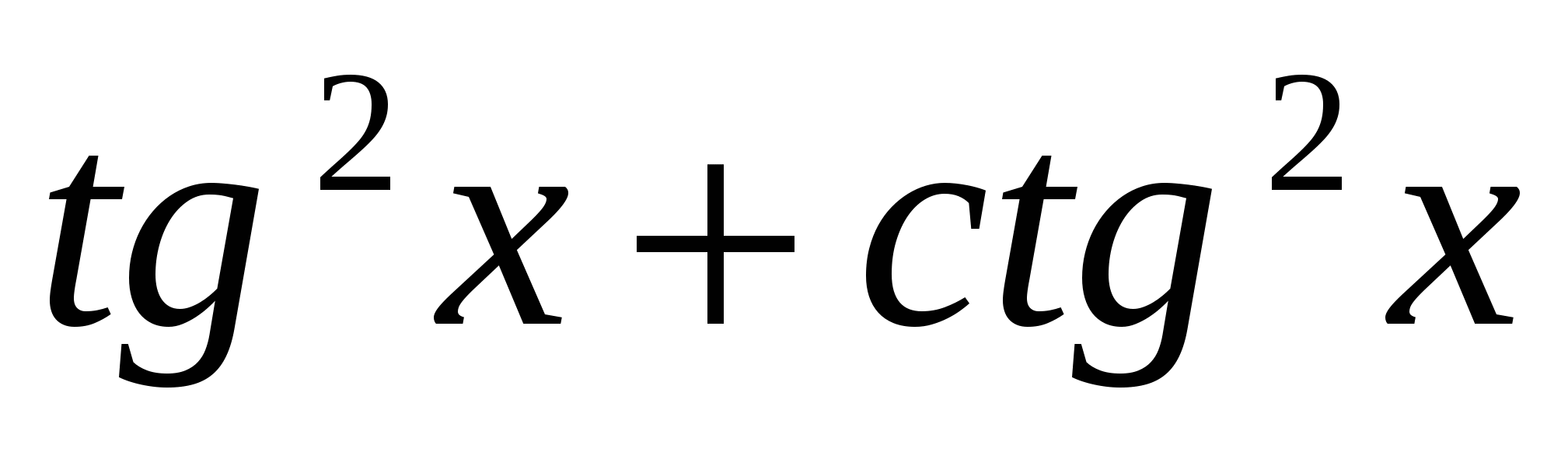 , если , если 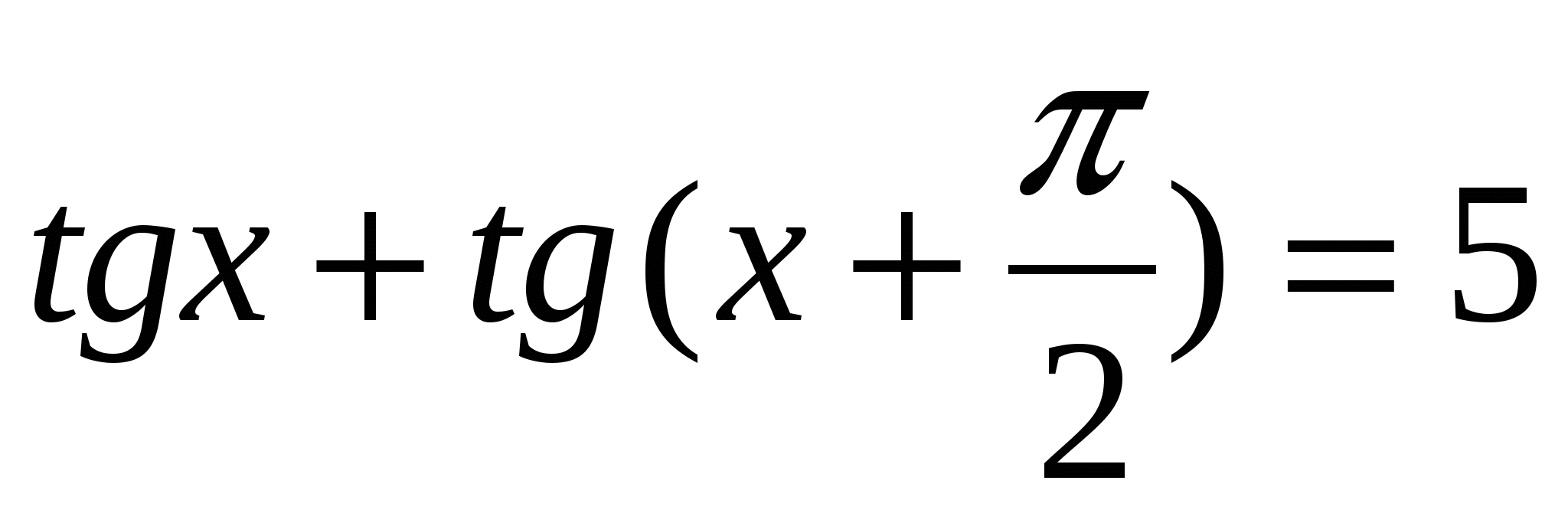 . .
1
|
2
|
3
|
4
|
5
|
Е27
|
25
|
23
|
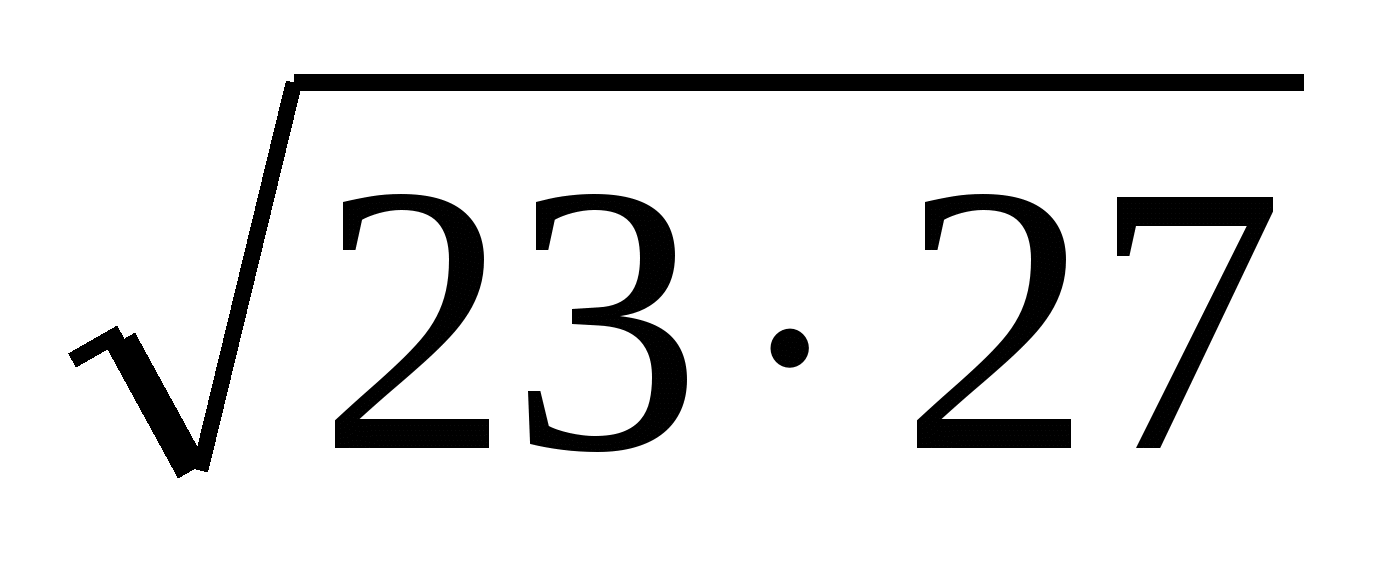
|
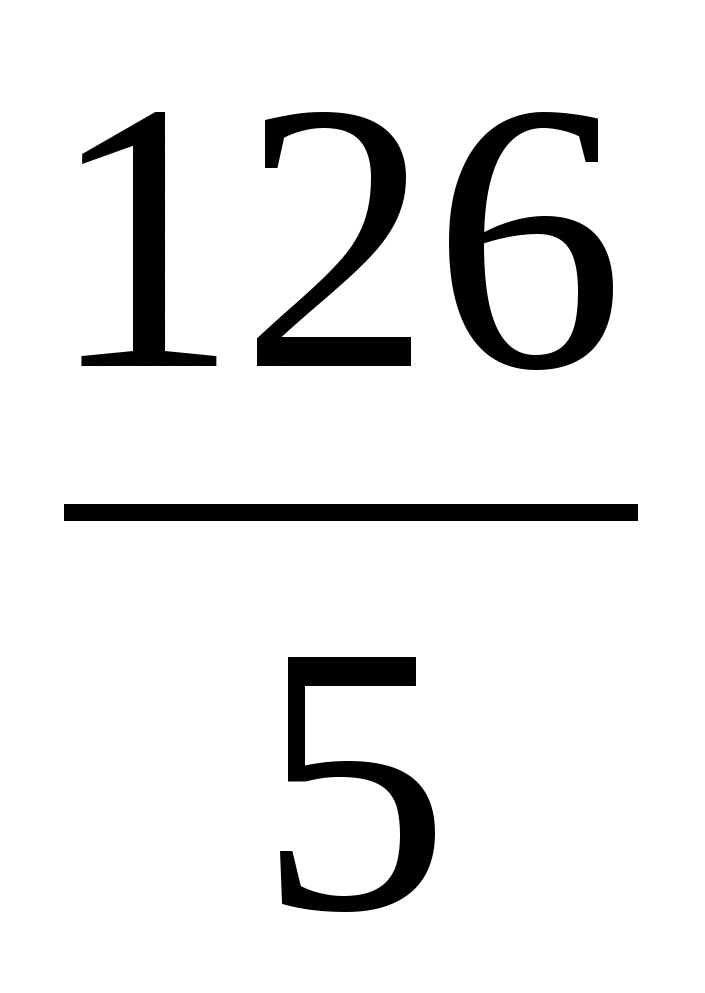
|
24. Упростить выражение 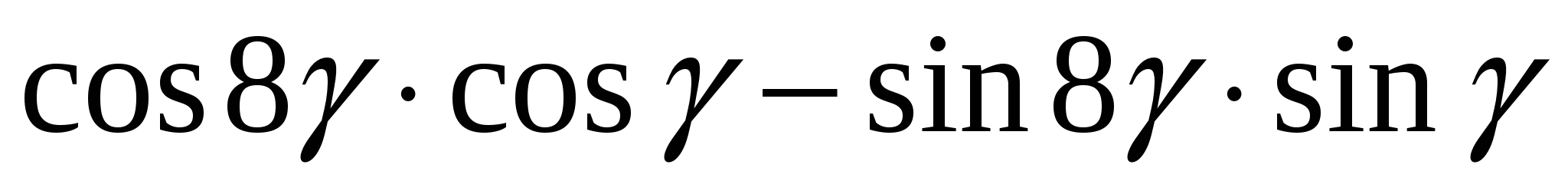 . .
1
|
2
|
3
|
4
|
5
|
sin 7
|
cos 7
|
sin 9
|
cos 9
|
cos 8
|
25. Упростить выражение sin(0,5+x) + cos(-x) + 3cos(2-x) :
1
|
2
|
3
|
4
|
5
|
5cosx
|
3cosx
|
cosx
|
sinx + 4cosx
|
среди ответов 1-4 нет правильного
|
13 группа.
Дополнительные задания для подготовки к экзаменам.
1. Вычислить 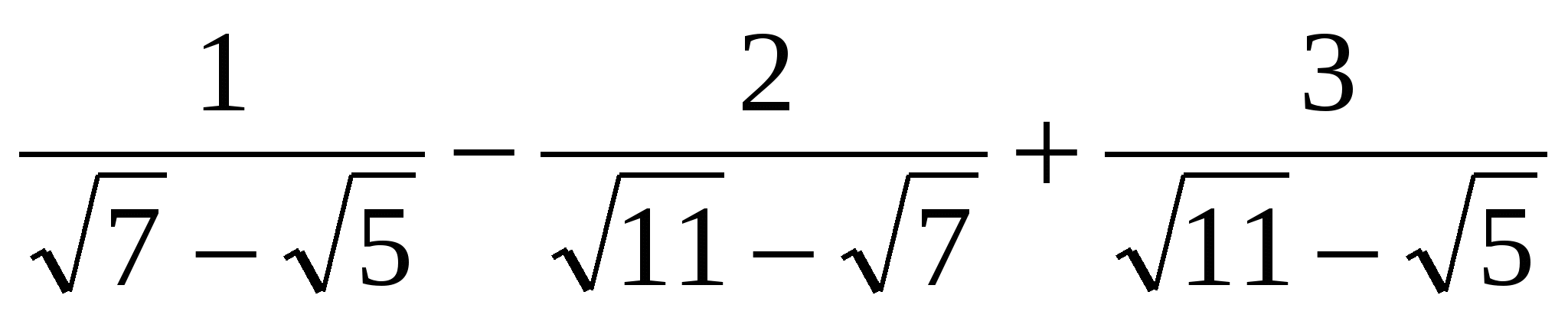 : :
2. Упростить выражение 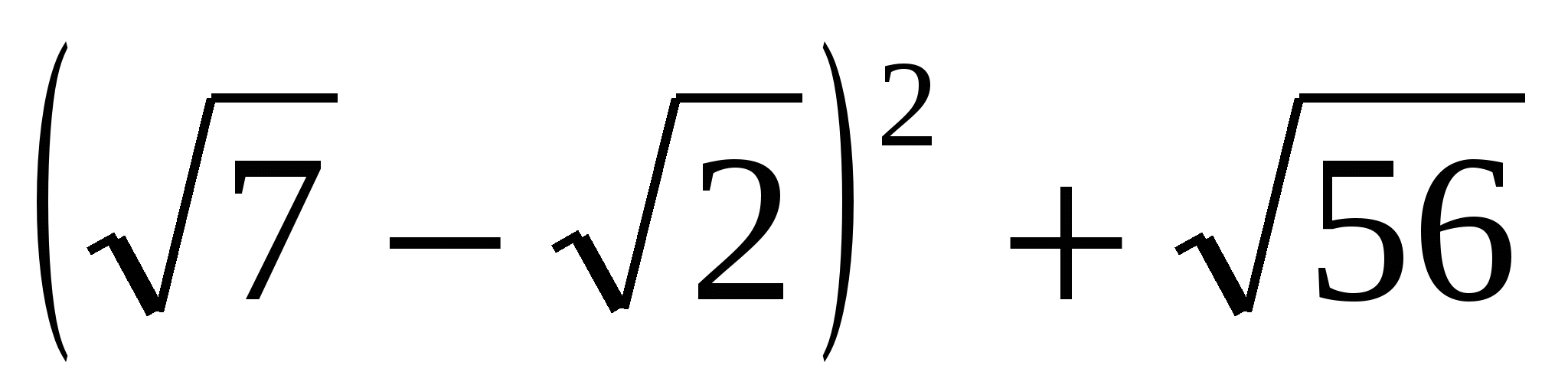 : :
1
|
2
|
3
|
4
|
5
|
5
|
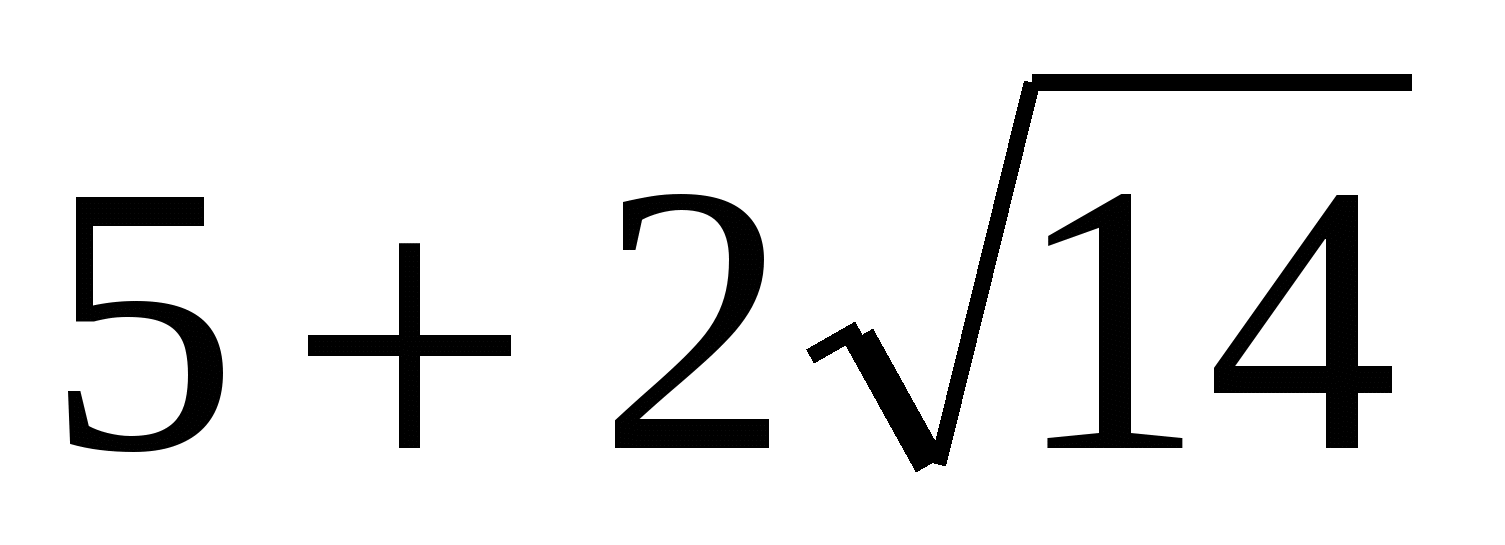
|
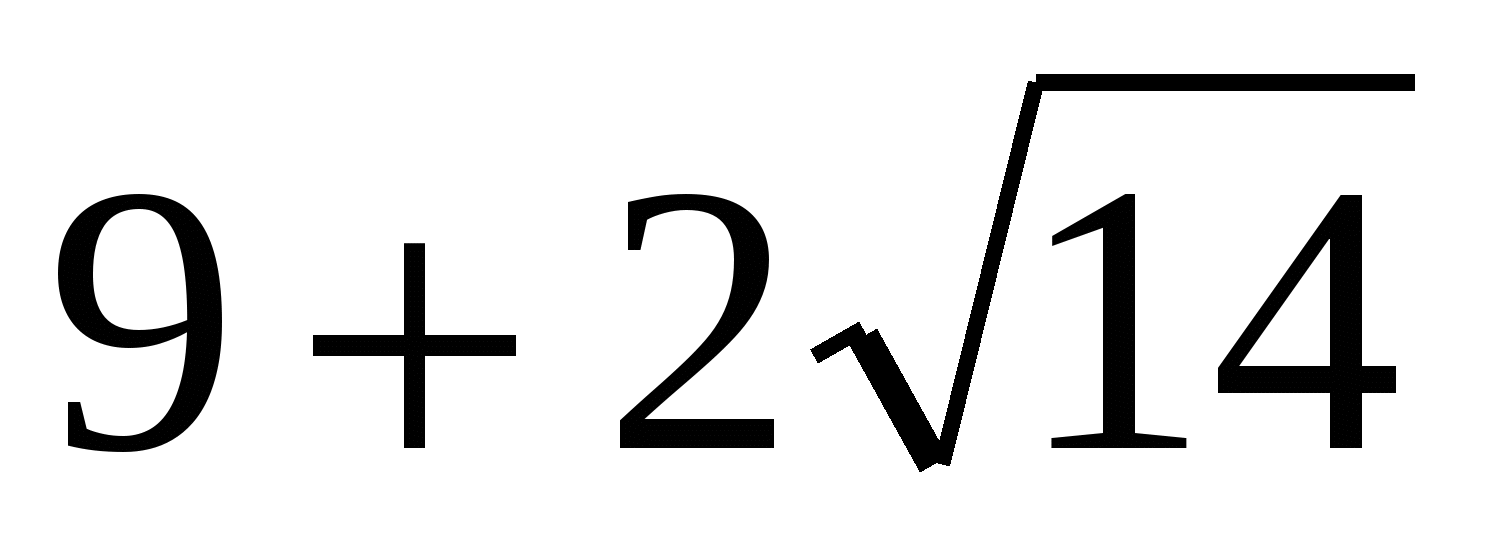
|
9
|
среди ответов 1-4 нет правильного
|
3. Смешали 30%-ный раствор соляной кислоты с 10%-ным и получили 400г 20%-ного раствора. 30%-ного раствора было взято
1
|
2
|
3
|
4
|
5
|
100 г
|
200 г
|
150 г
|
250 г
|
300 г
|
4. При каком значении в один корень уравнения 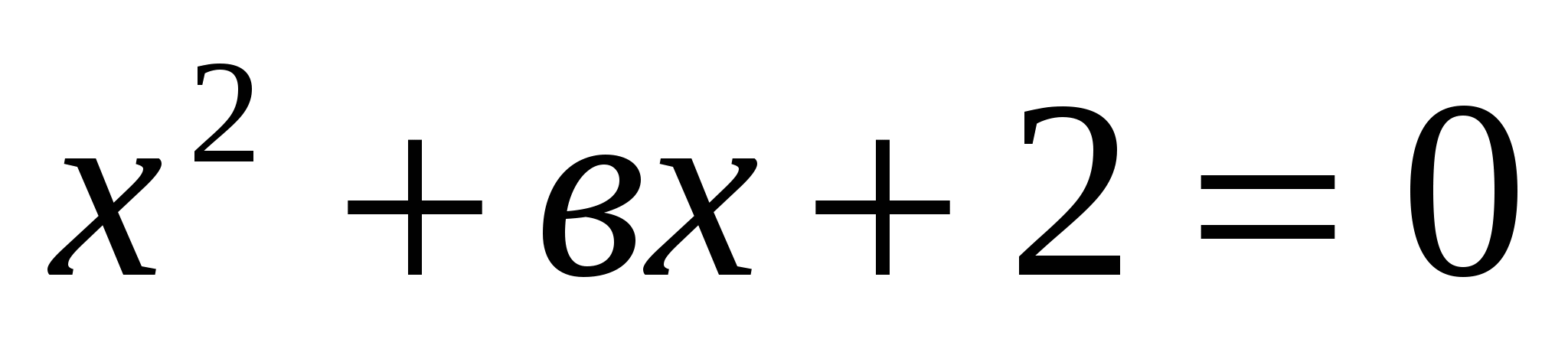 вдвое больше другого ? вдвое больше другого ?
5. Если корни квадратного уравнения 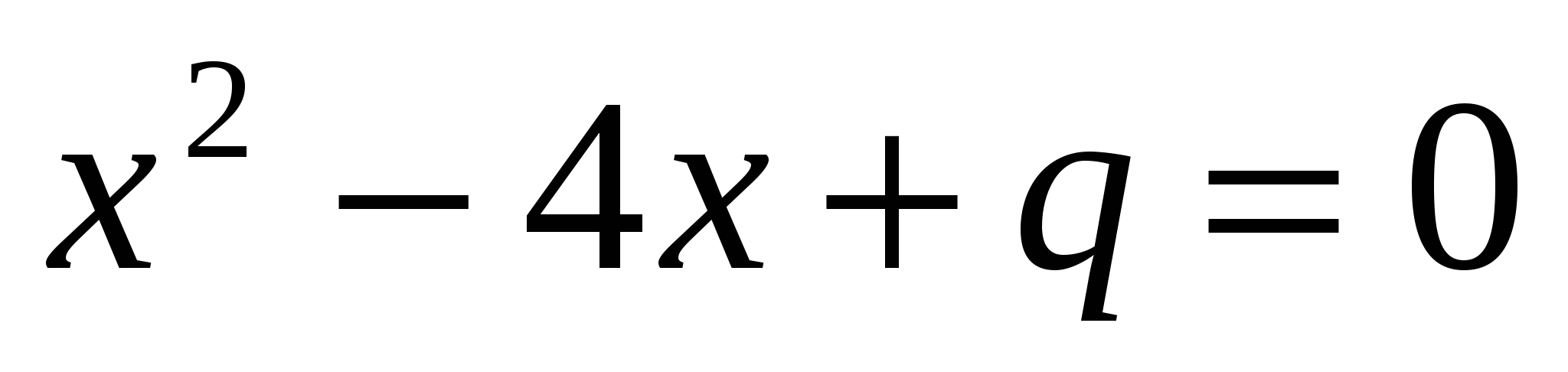 удовлетворяют условию удовлетворяют условию  , то q равно , то q равно
1
|
2
|
3
|
4
|
5
|
-45
|
39
|
60
|
-55
|
45
|
6. Серединой отрезка, являющегося решением двойного неравенства 1 3 - 2х 9, является число
7. Решение неравенства 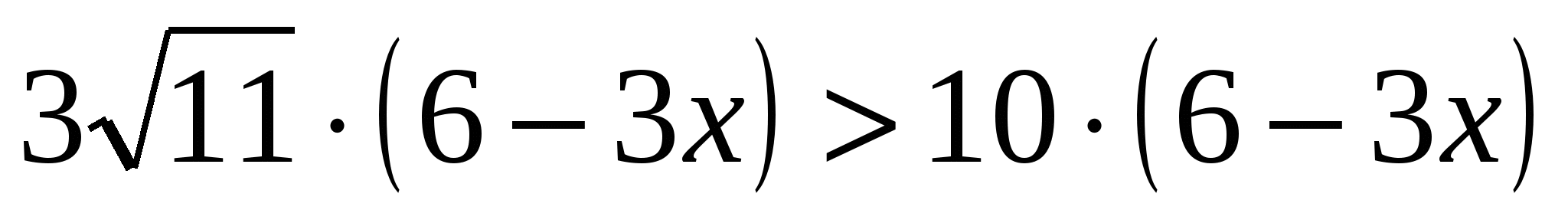 определяется соотношением определяется соотношением
1
|
2
|
3
|
4
|
5
|
x > 0,5
|
x < 0,5
|
x < 2
|
x > 2
|
нет решений
|
8. Произведение корней уравнения 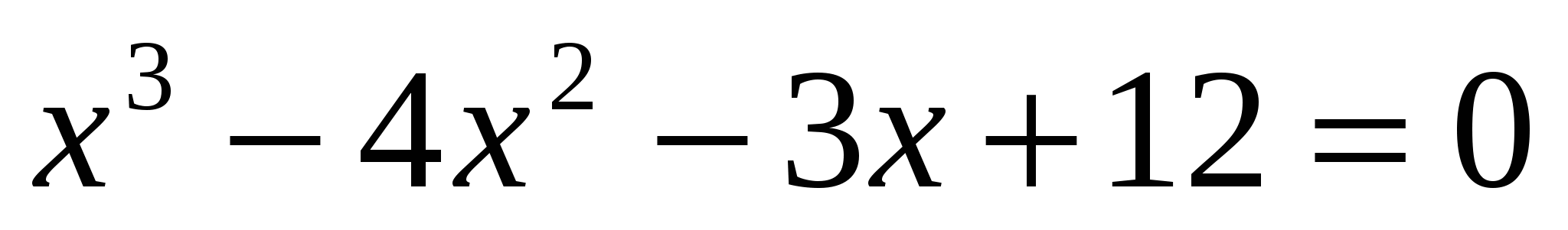 равно равно
1
|
2
|
3
|
4
|
5
|
12
|
16
|
-10
|
-12
|
-8
|
9. Сумма наибольшего отрицательного и наименьшего положительного корней уравнения 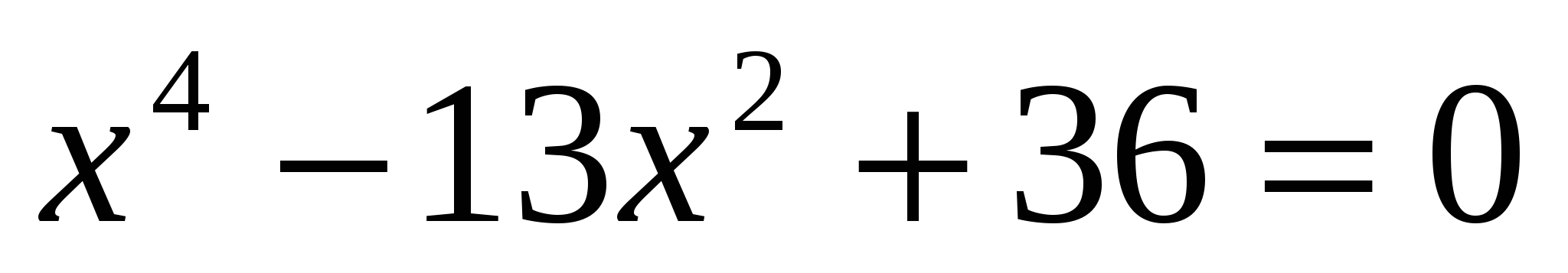 равна равна
10. Найти значение выражения 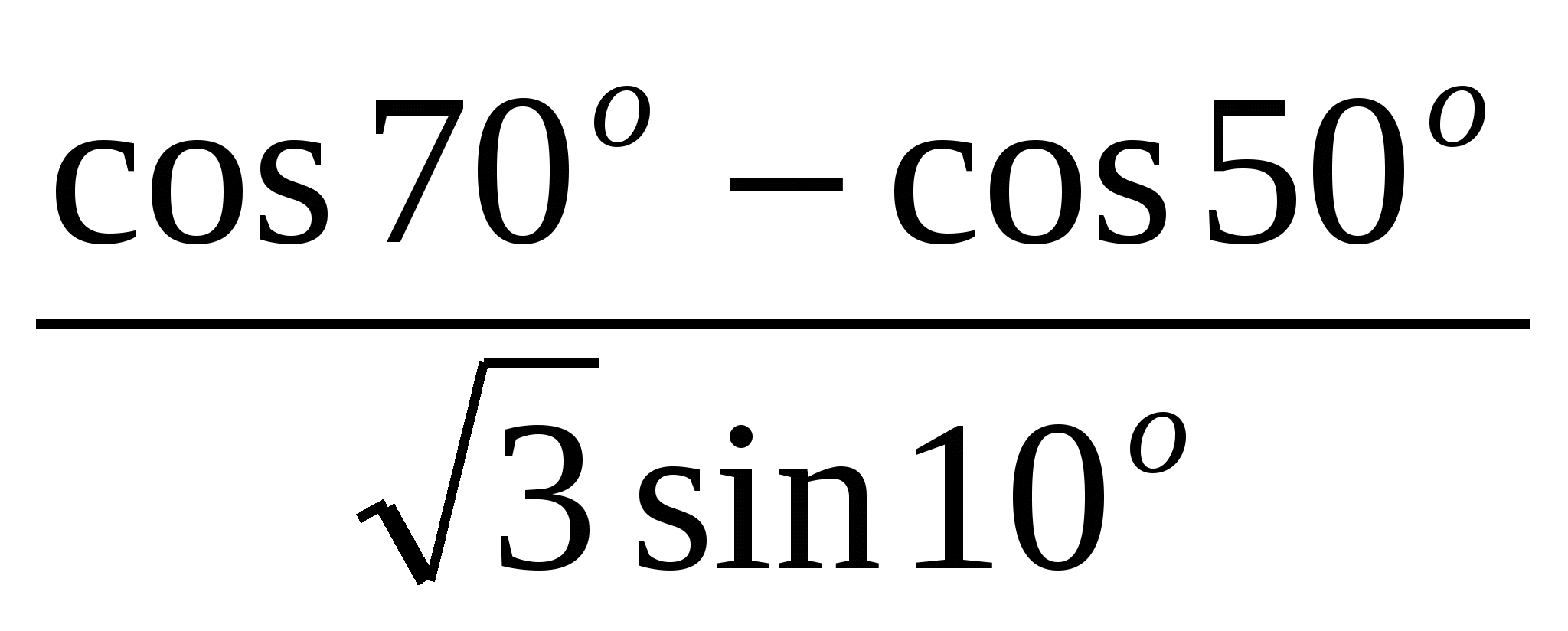 : :
1
|
2
|
3
|
4
|
5
|
1
|
2
|
-0,5
|
-1
|
среди ответов 1-4 нет правильного
|
11. Все решения неравенства 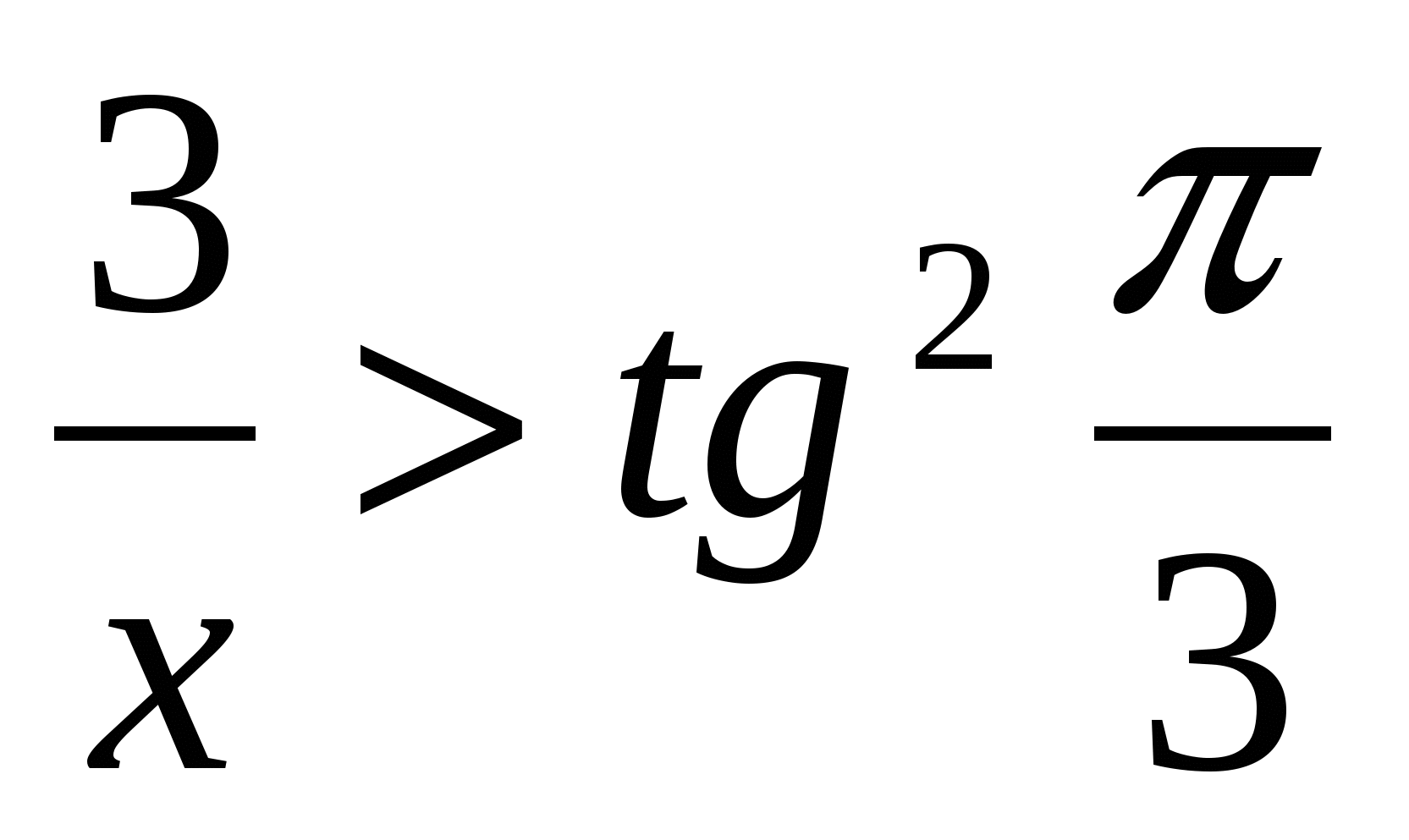 образуют множество образуют множество
1
|
2
|
3
|
4
|
5
|
( -; 1 )
|
( 0; 9 )
|
( 0; 1 )
|
( 1; + )
|
(-; 0)(1; +)
|
Таблица для внесения ответов к тестам:
№ вопроса
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
Ваш вариант ответа
|
|
|
|
|
|
|
|
|
|
|
|
Указания к задачам теста:
Наиболее рациональное решение – начать с освобождения от иррациональностей в знаменателях дробей;
Не забудьте о вынесении множителя из-под знака корня;
4,5. Задачи подразумевают применение теоремы Виета.
Будет неразумно начать с раскрытия скобок. Изучите вид этого
неравенства повнимательнее.
Вспомните один из трёх общих методов решения уравнений! И ещё:
находя произведение корней квадратного уравнения, помните о
теореме Виета!
Будьте особенно внимательны, составляя требуемую сумму: что с чем
складыаете!
Аккуратно примените нужную тригонометрическую формулу.
Помните, что 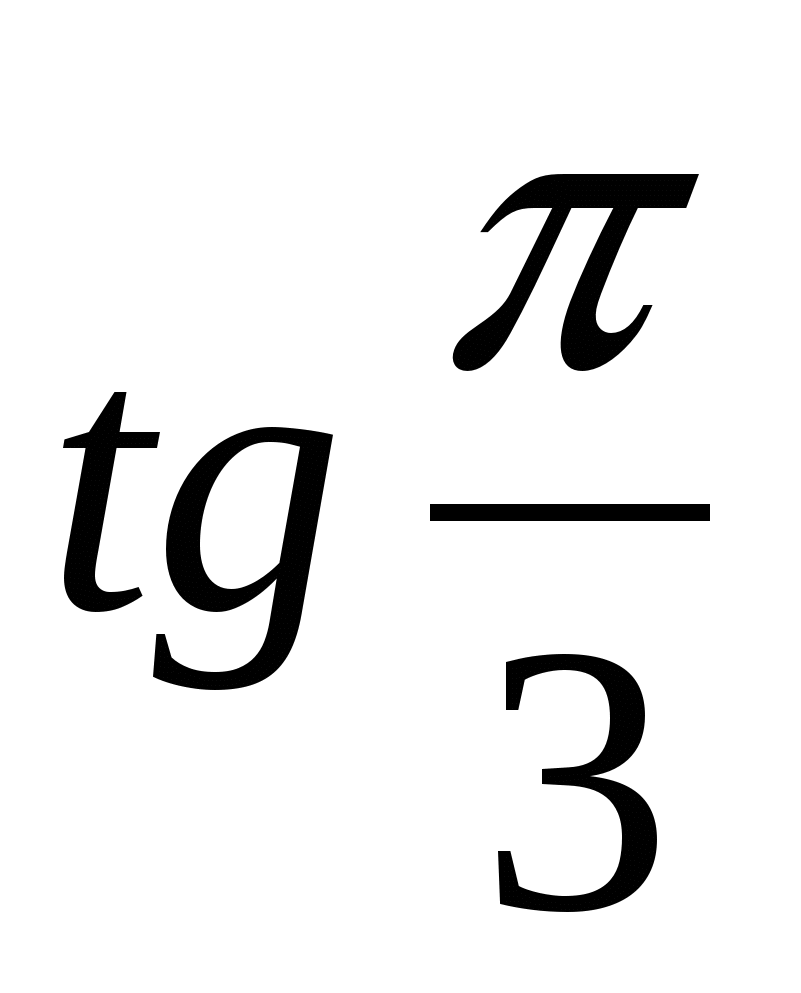 - это конкретное число. Подставив его значение, - это конкретное число. Подставив его значение,
получите неравенство, которое решается методом интервалов !
Общие рекомендации при подготовке к экзамену:
Учите формулы, правила, алгоритмы и т.д. !!!
Прорешайте заново имеющиеся у Вас в папке тесты по темам, изученным в I семестре. Ваша цель – найти вопросы, вызывающие у Вас затруднения, и задать их на консультации 29 декабря в 14 часов. Особо тщательно отработайте задачи, в которых Вы допускали ошибки во время прошлых тестов ( для этого Вам возвращались проверенные протоколы с ответами и выдавались тексты тестов ).
Обратите особое внимание на темы, изученные в сентябре – октябре, т.к. они могут быть подзабыты из-за давности времени.
|
|
|
 Скачать 165.08 Kb.
Скачать 165.08 Kb.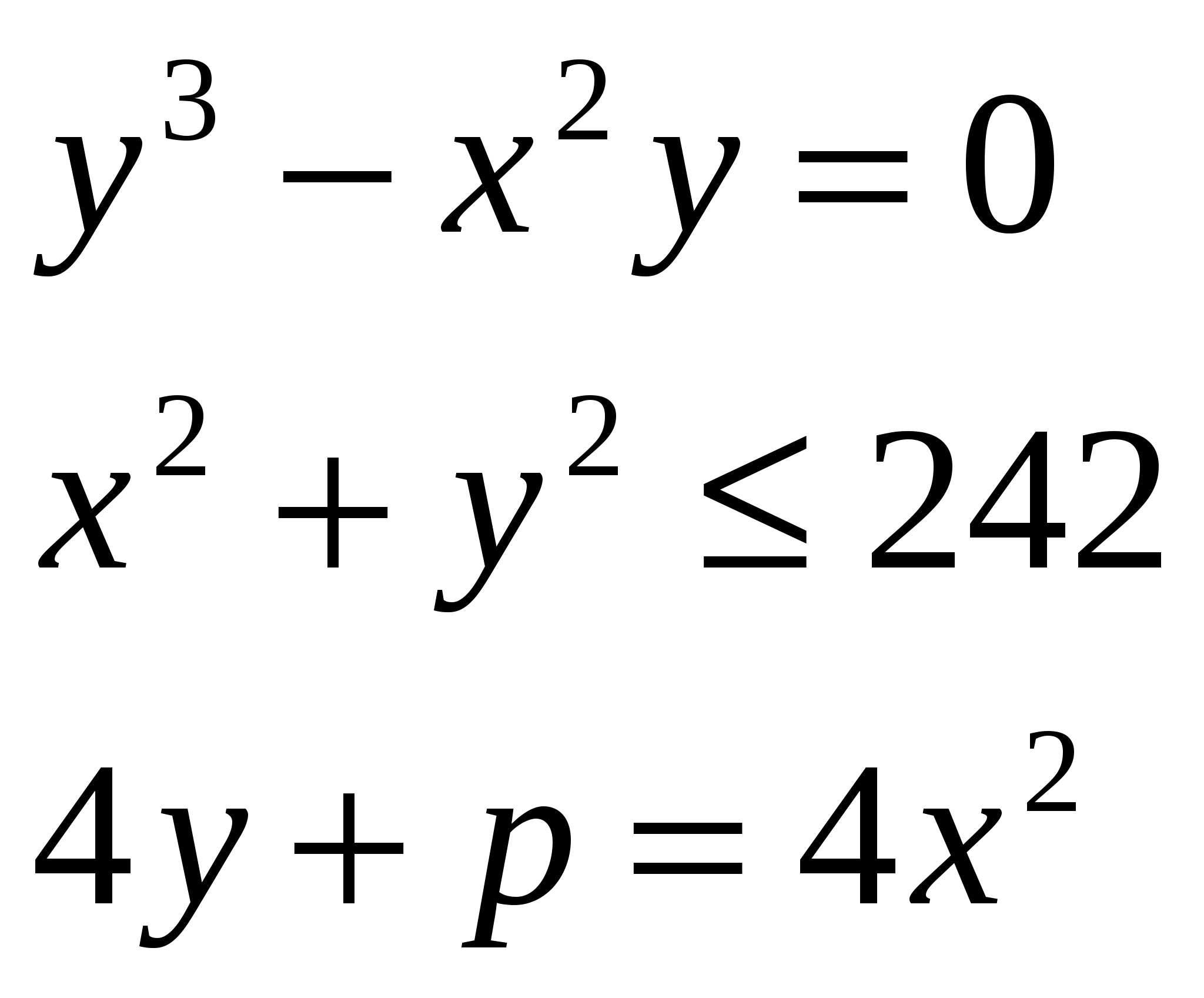 имеет ровно два различных решения? Остаток от деления на 5 равен
имеет ровно два различных решения? Остаток от деления на 5 равен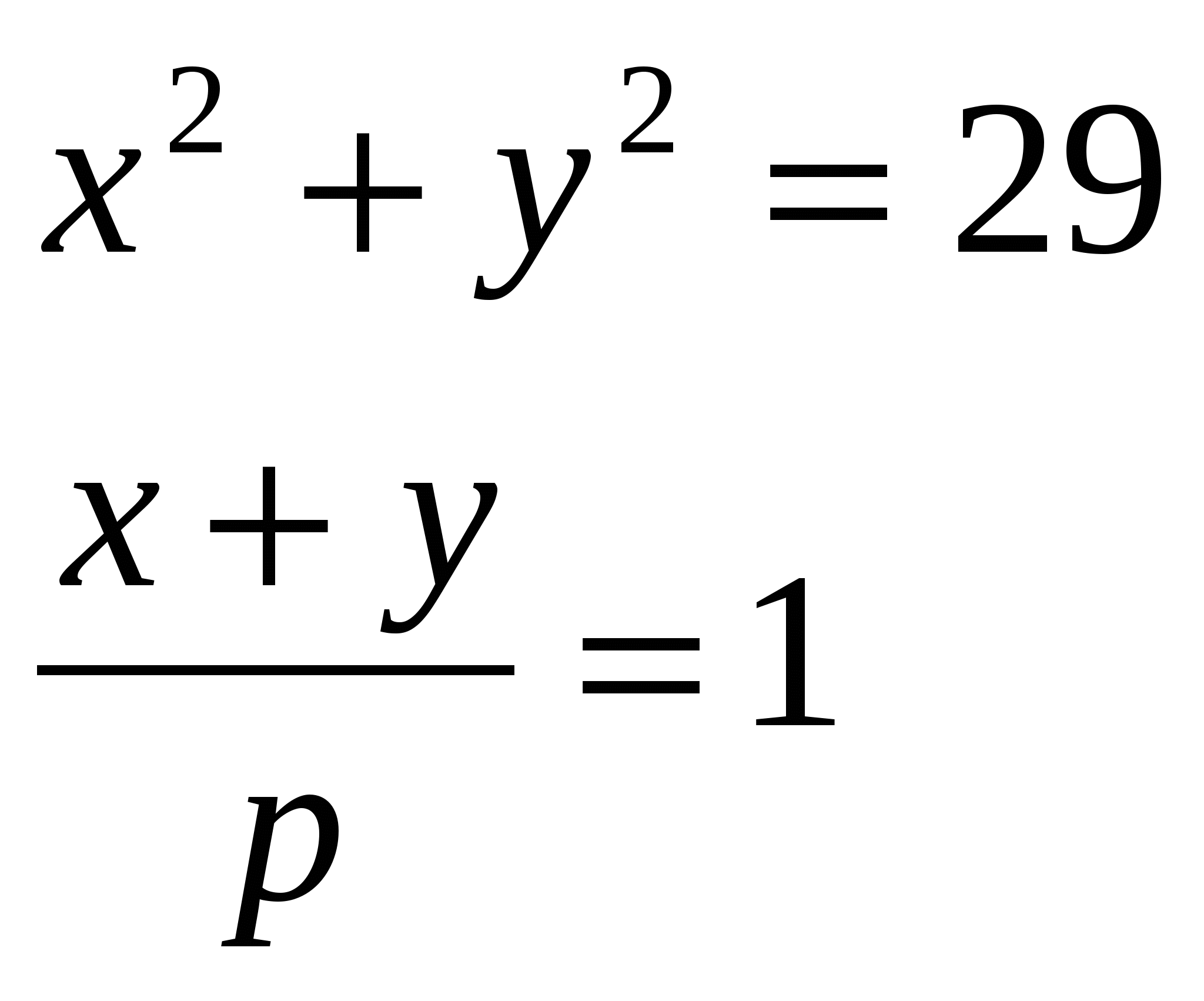 имеет ровно два различных решения?
имеет ровно два различных решения?