Главная страница
Анализ
Анкета
архив
Биография
Бюллетень
Викторина
Глава
Диплом
Доклад
Документация
Задача

Решение показательных уравнений и неравенств



Скачать 46.45 Kb.
НазваниеРешение показательных уравнений и неравенств
Дата05.03.2016
Размер46.45 Kb.
ТипУрок


Тема урока: Решение показательных уравнений и неравенств.
Цели урока:

  1. Обобщить и систематизировать знания и умения учащихся, связанные с решением показательных уравнений и неравенств.

  2. Повторить основные способы решения показательных уравнений и неравенств.

  3. Воспитывать способность следовать нормам поведения.

  4. Показать возможности применения ПК на уроках математики.


Технические средства и оформление: ПК, тестовая оболочка, мультимедийная презентация, карточки для учащихся.
План урока:


  1. Оргмомент.

  2. Проверка домашнего задания.

  3. Повторение теоретического материала.

  4. Устная работа.

  5. Самостоятельная тестовая работа.

  6. Устная работа.

  7. Дифференцированная работа:

  1. тестирование с помощью ПК;

  2. работа по карточкам;

  3. работа с учебником.

  1. Устная работа.

  2. Подведение итогов урока.

  3. Домашнее задание.



Ход урока:


  1. Организационный момент: проверка готовности класса к уроку, проверка отсутствующих.




  1. Проверка домашнего задания. Из домашнего задания на доске разбираются задания, вызвавшие у учеников затруднения при их выполнении дома.



  1. Повторение теоретического материала.

Учитель: А сейчас вспомним основные вопросы, связанные с решением показательных уравнений и неравенств:

    1. Какие уравнения (неравенства) называются показательными?

    2. Какие основные способы решения показательных уравнений вы знаете?

    3. На что необходимо обратить внимание при решении показательных неравенств?

    4. Каким способом можно решить




А) уравнение вида ;
Б) неравенство вида ?


  1. Устная работа.

Учитель: Давайте устно решим уравнения и неравенства.

1.Решить уравнения: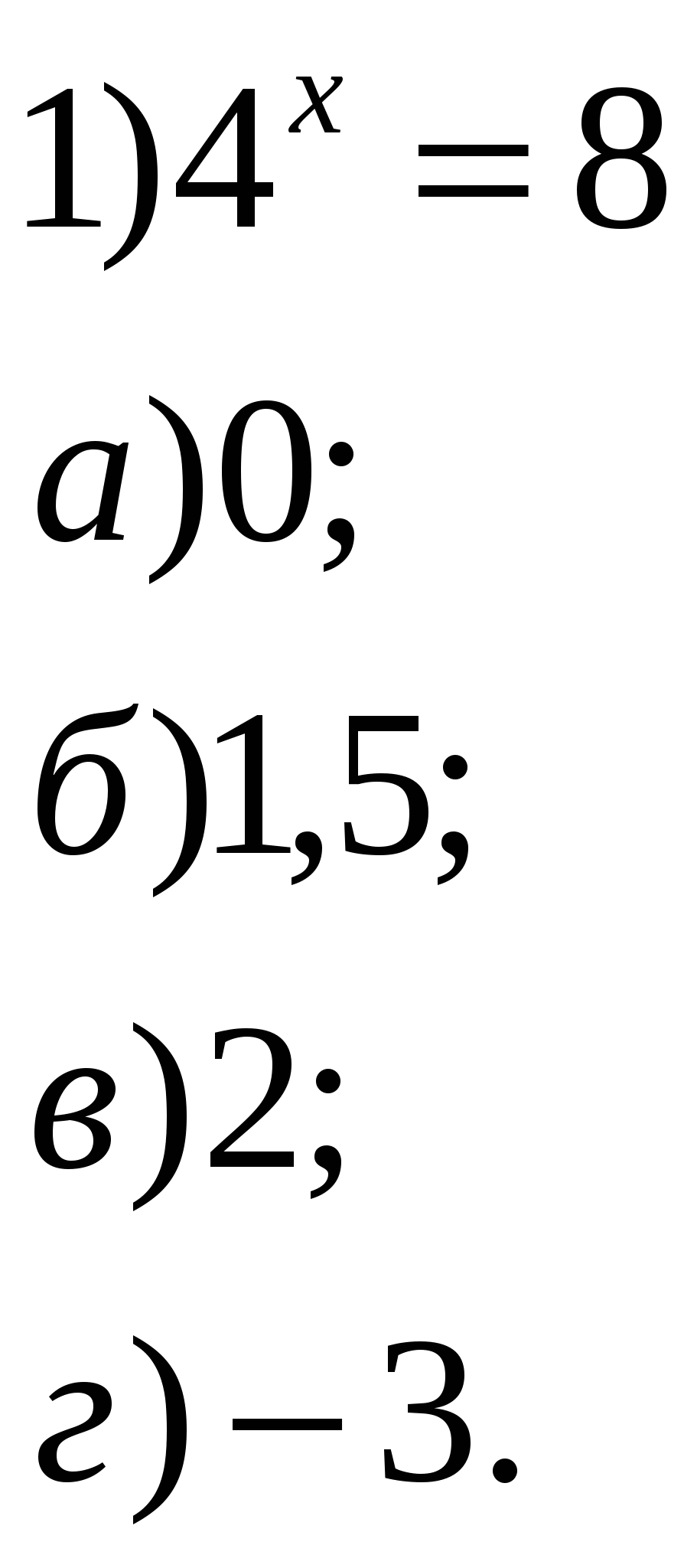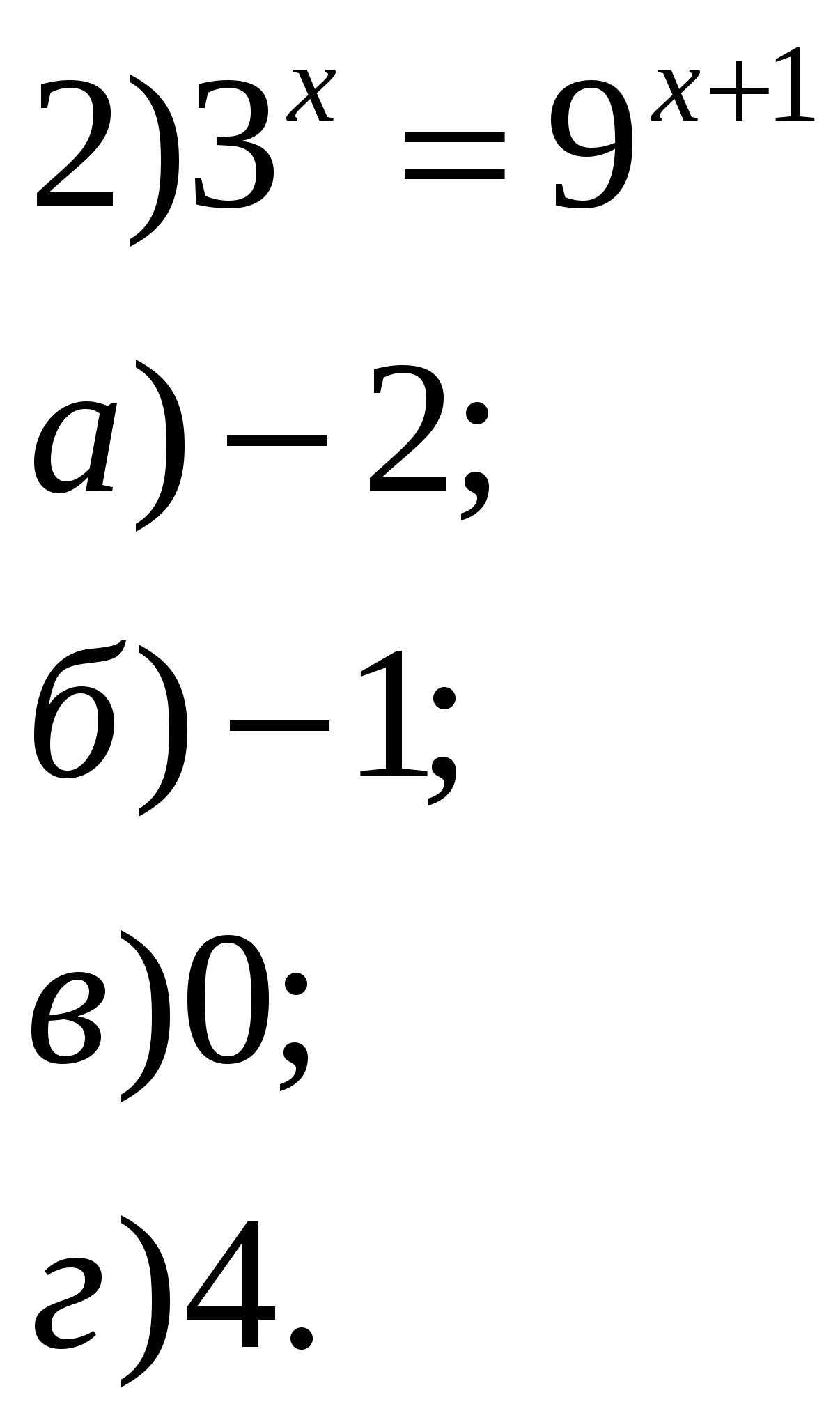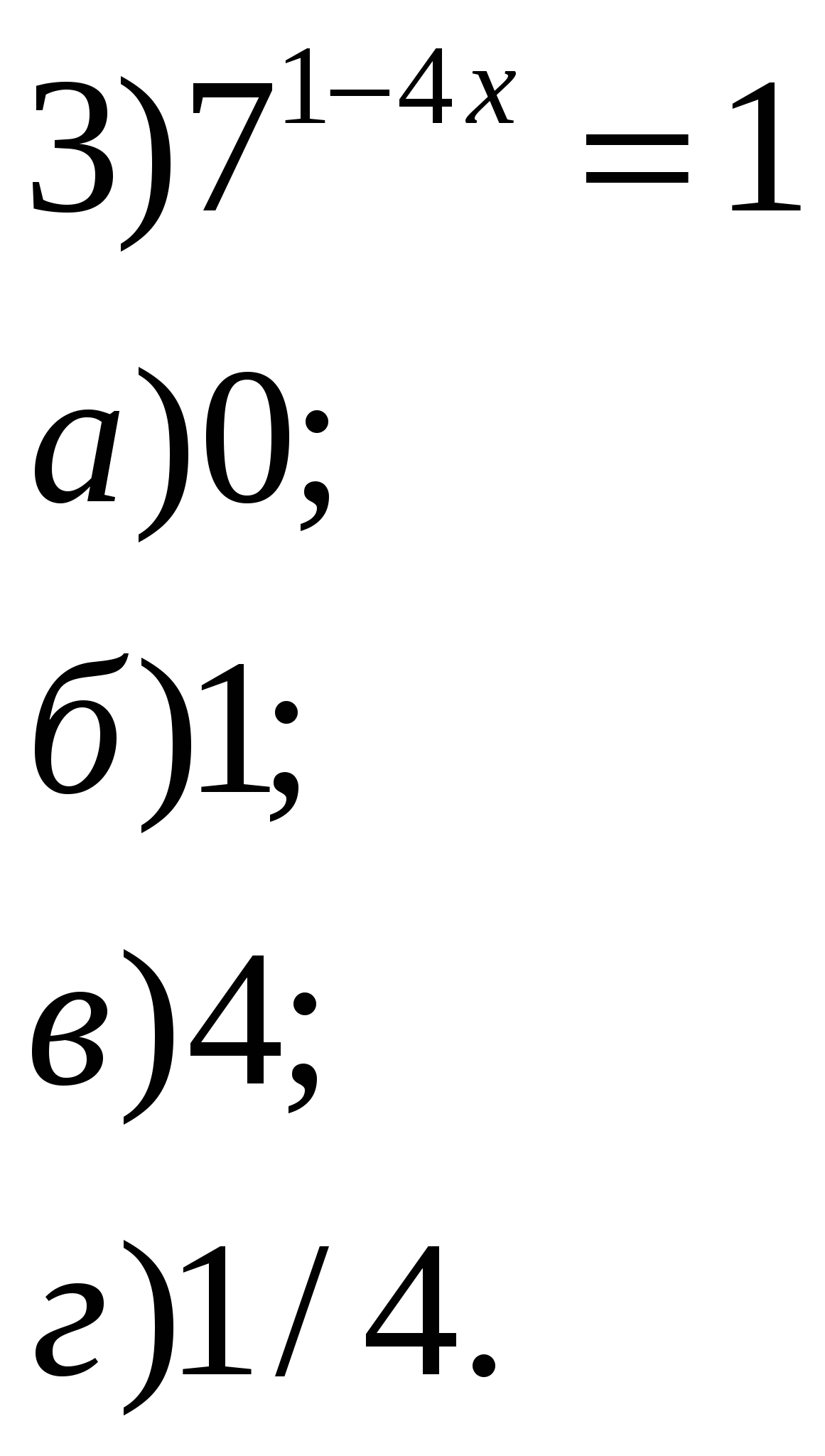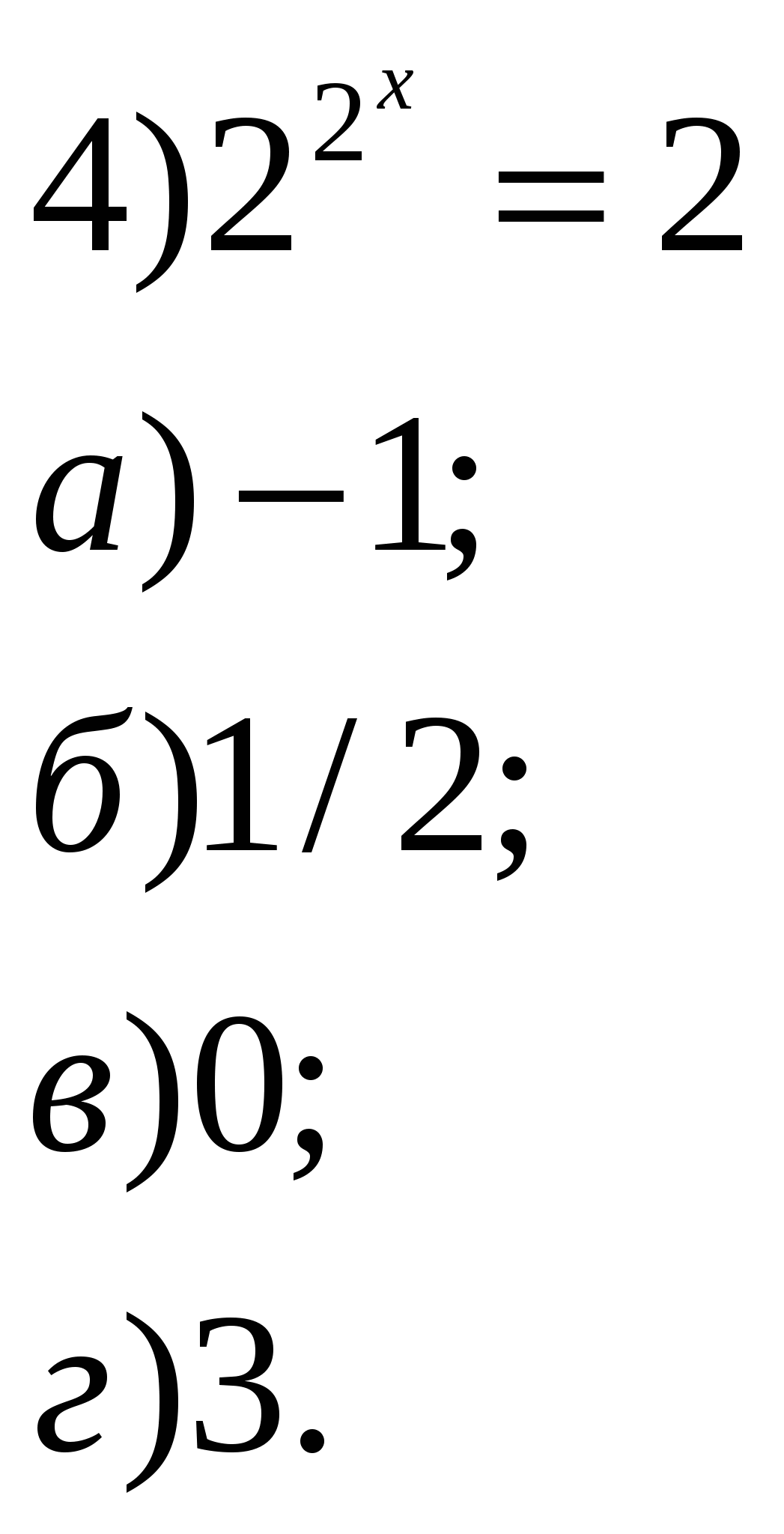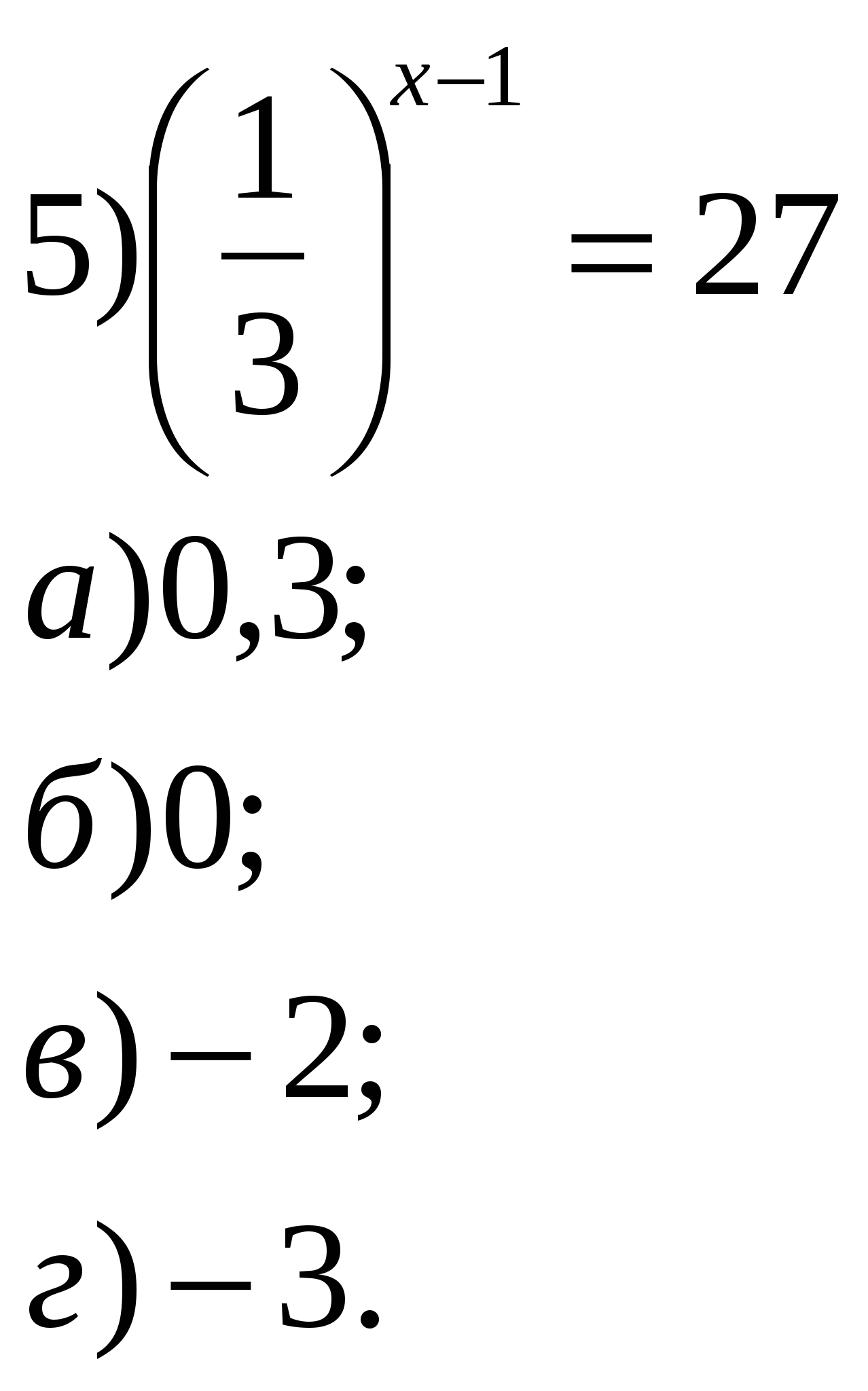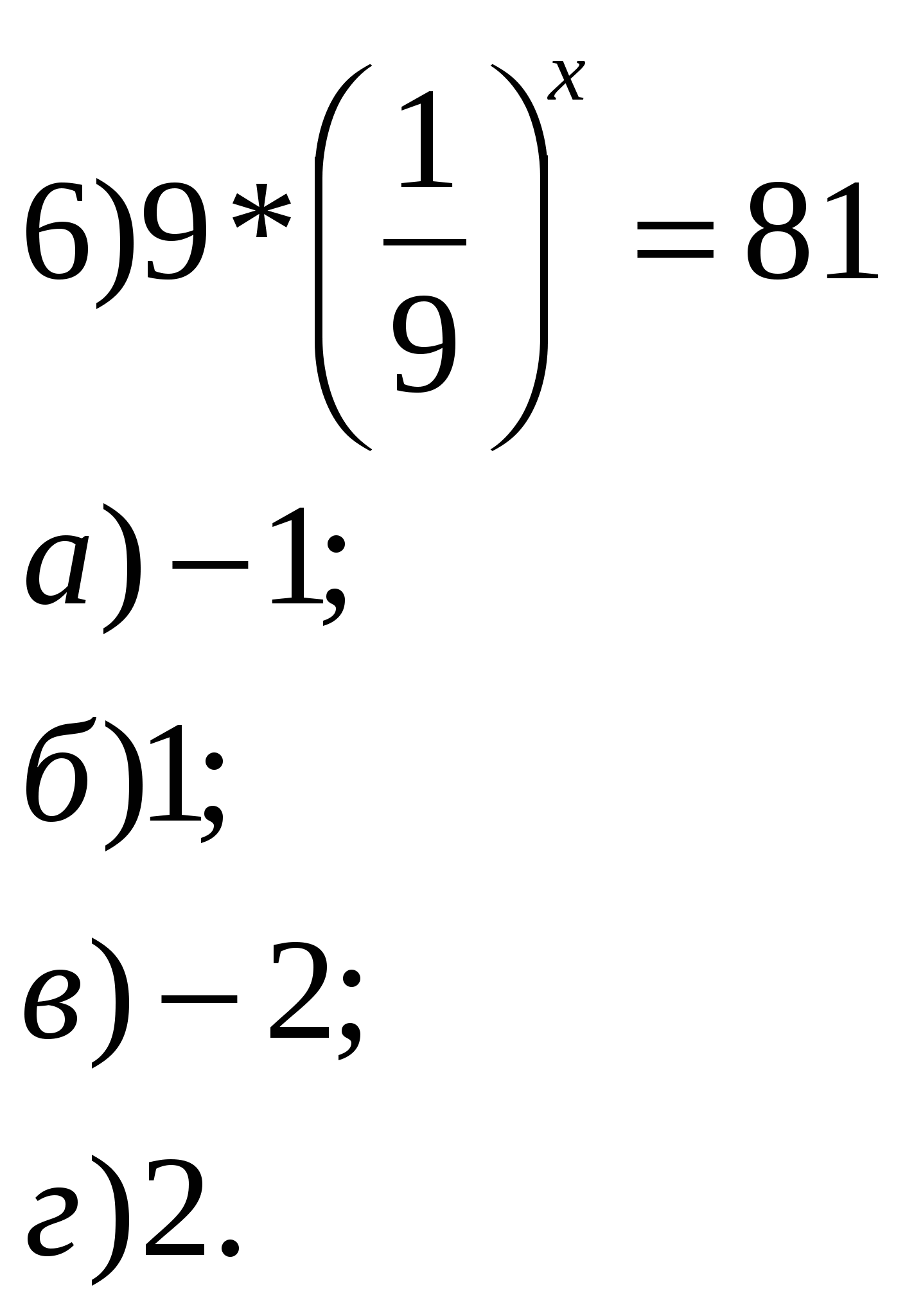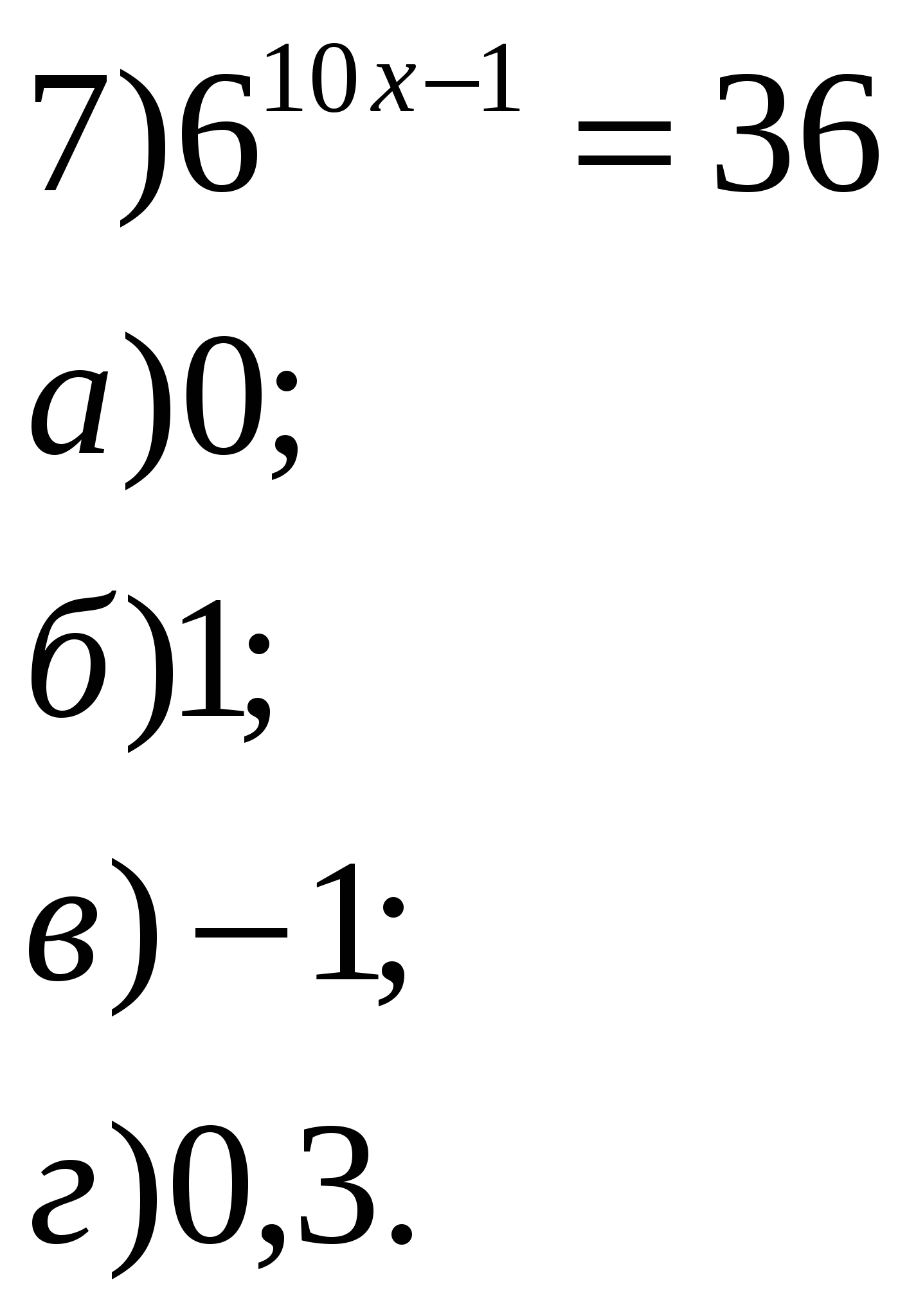










2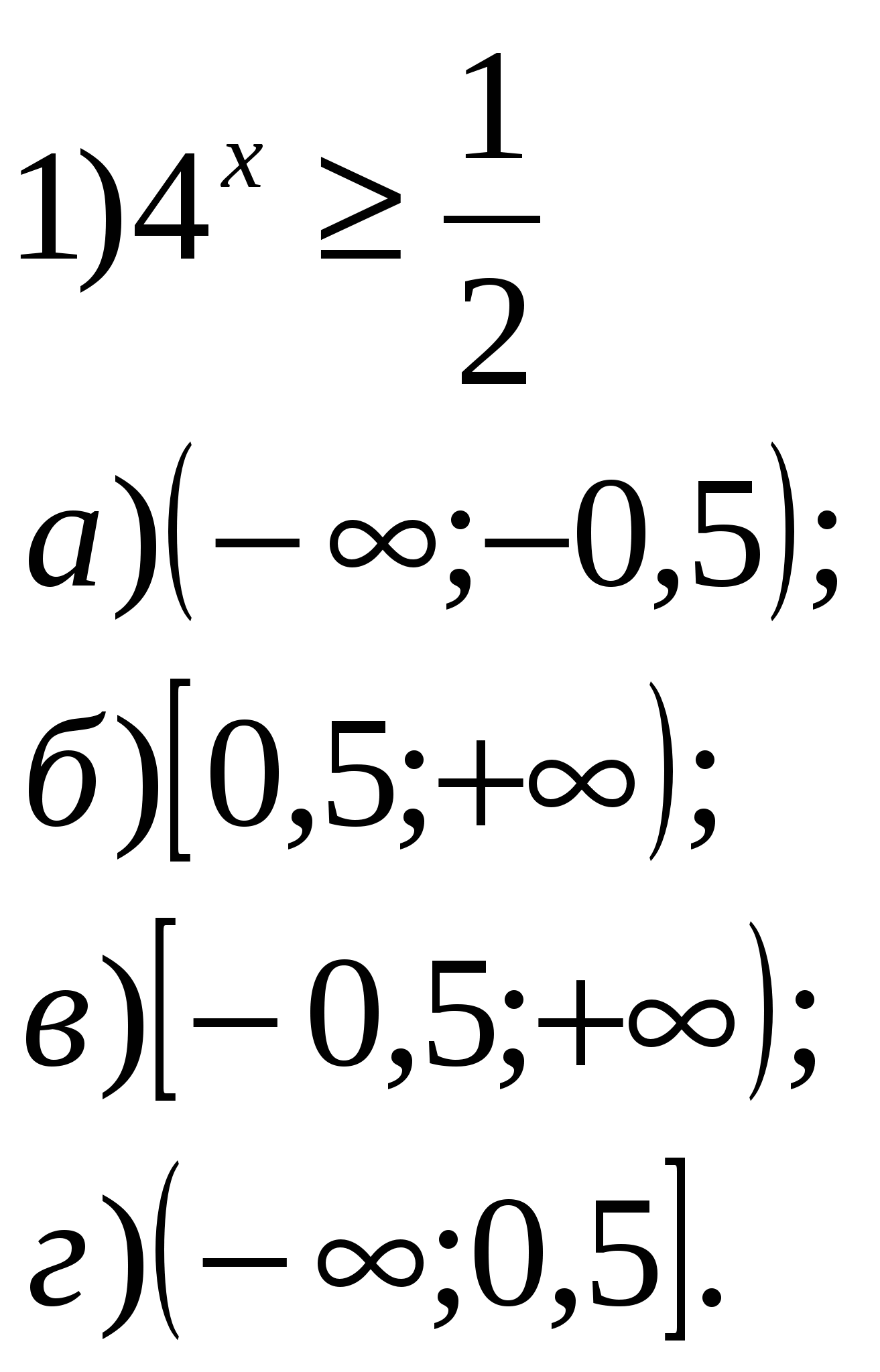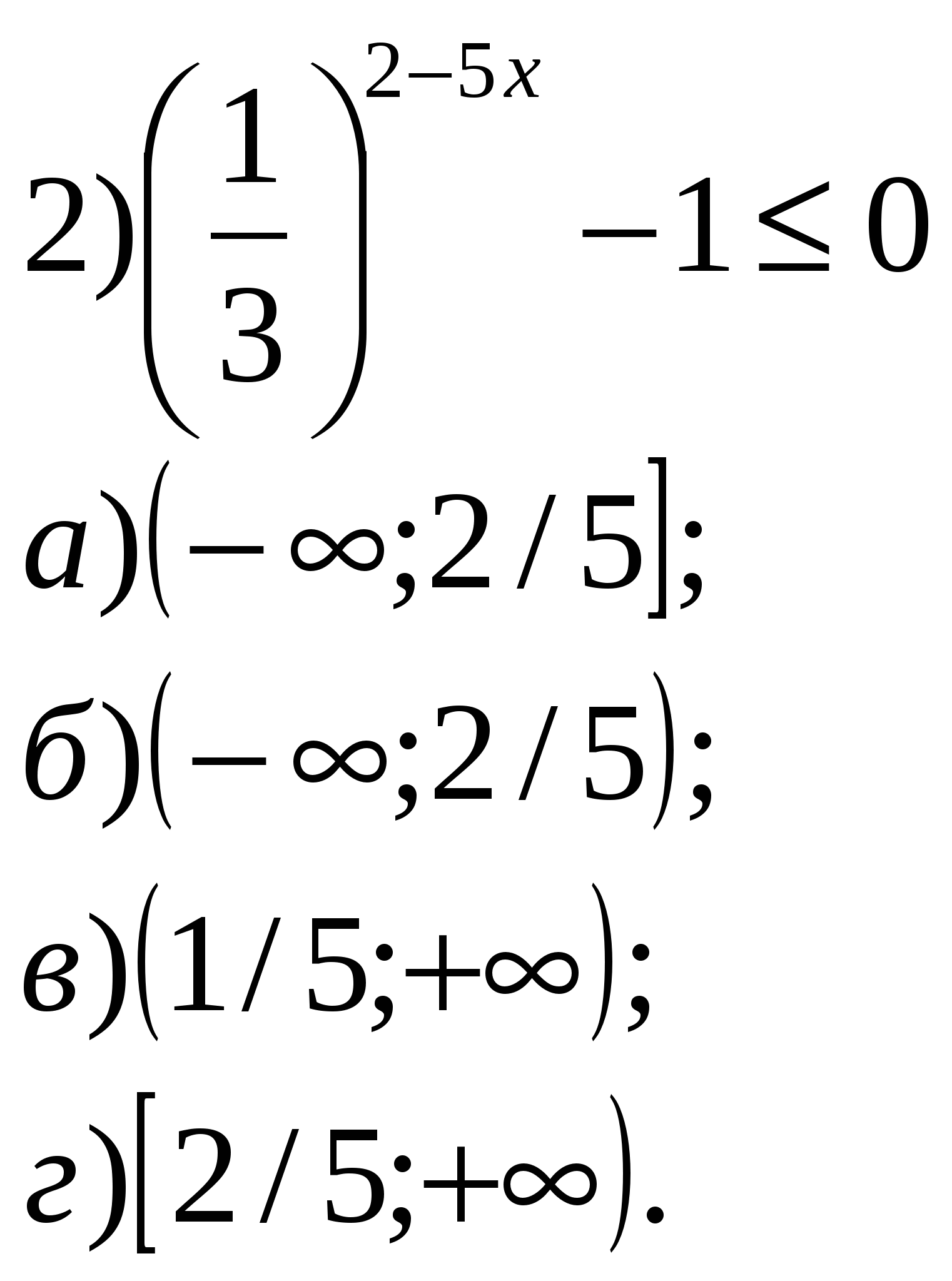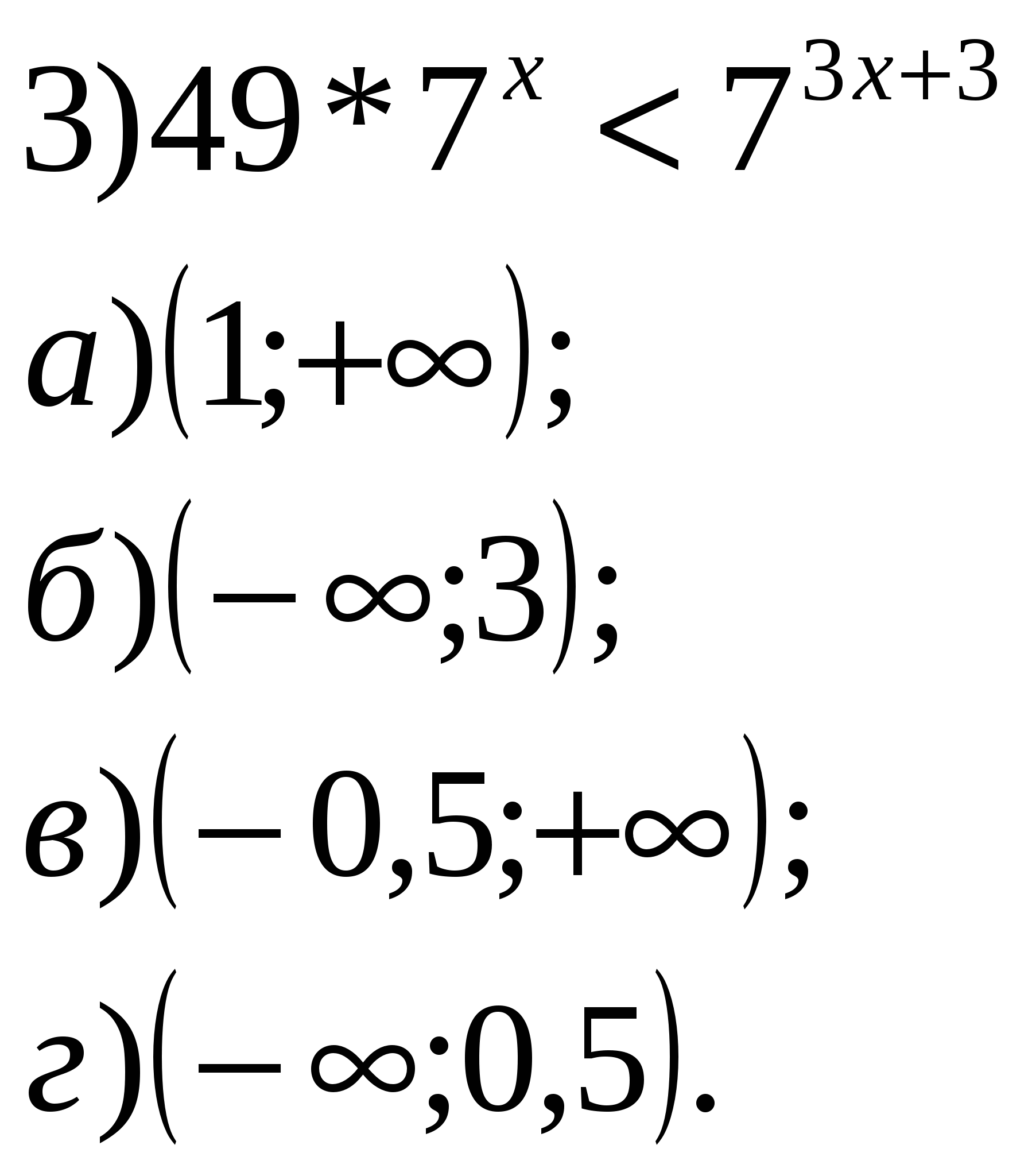


.Решить неравенства:
3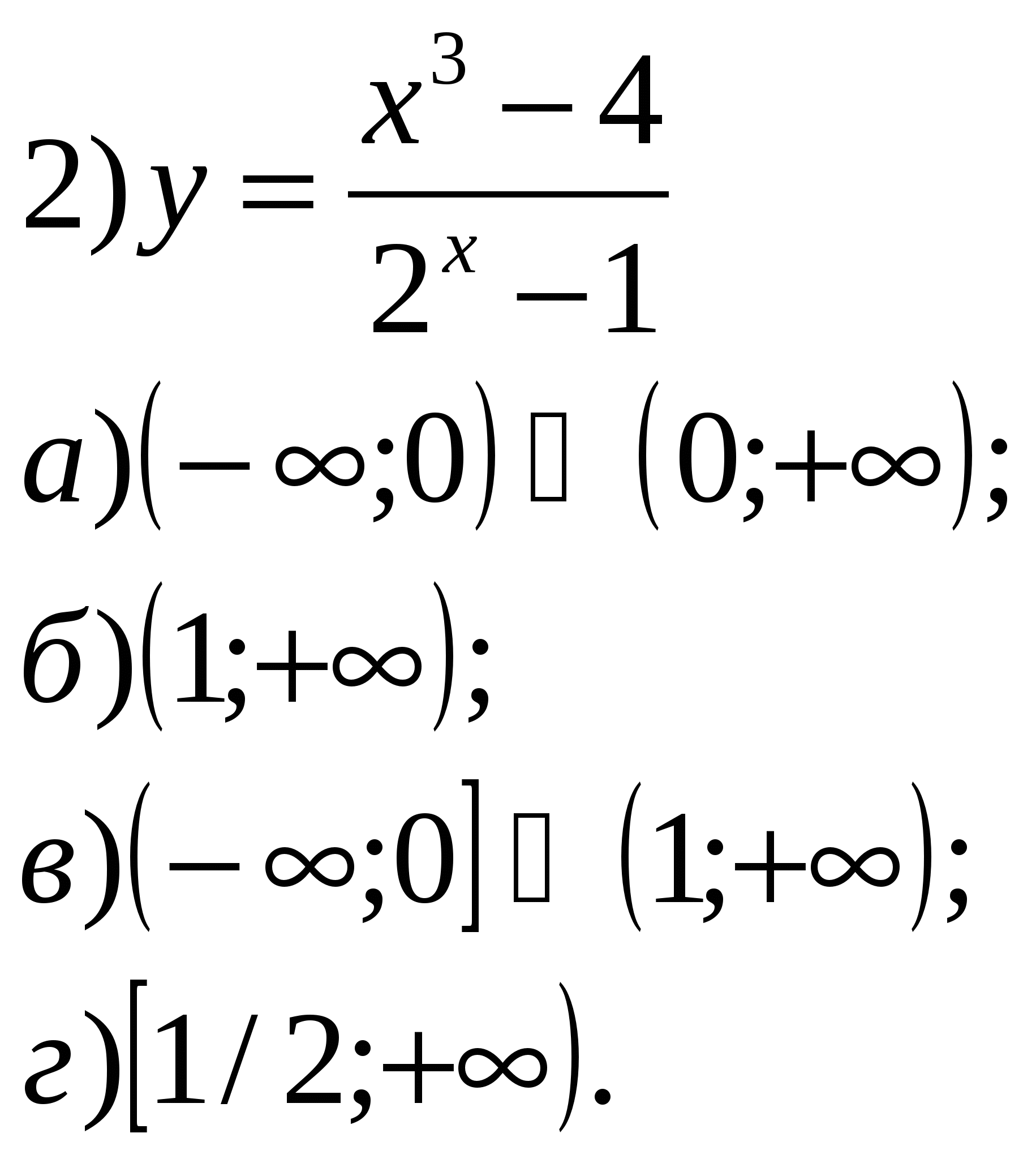
. Найти область определения функции: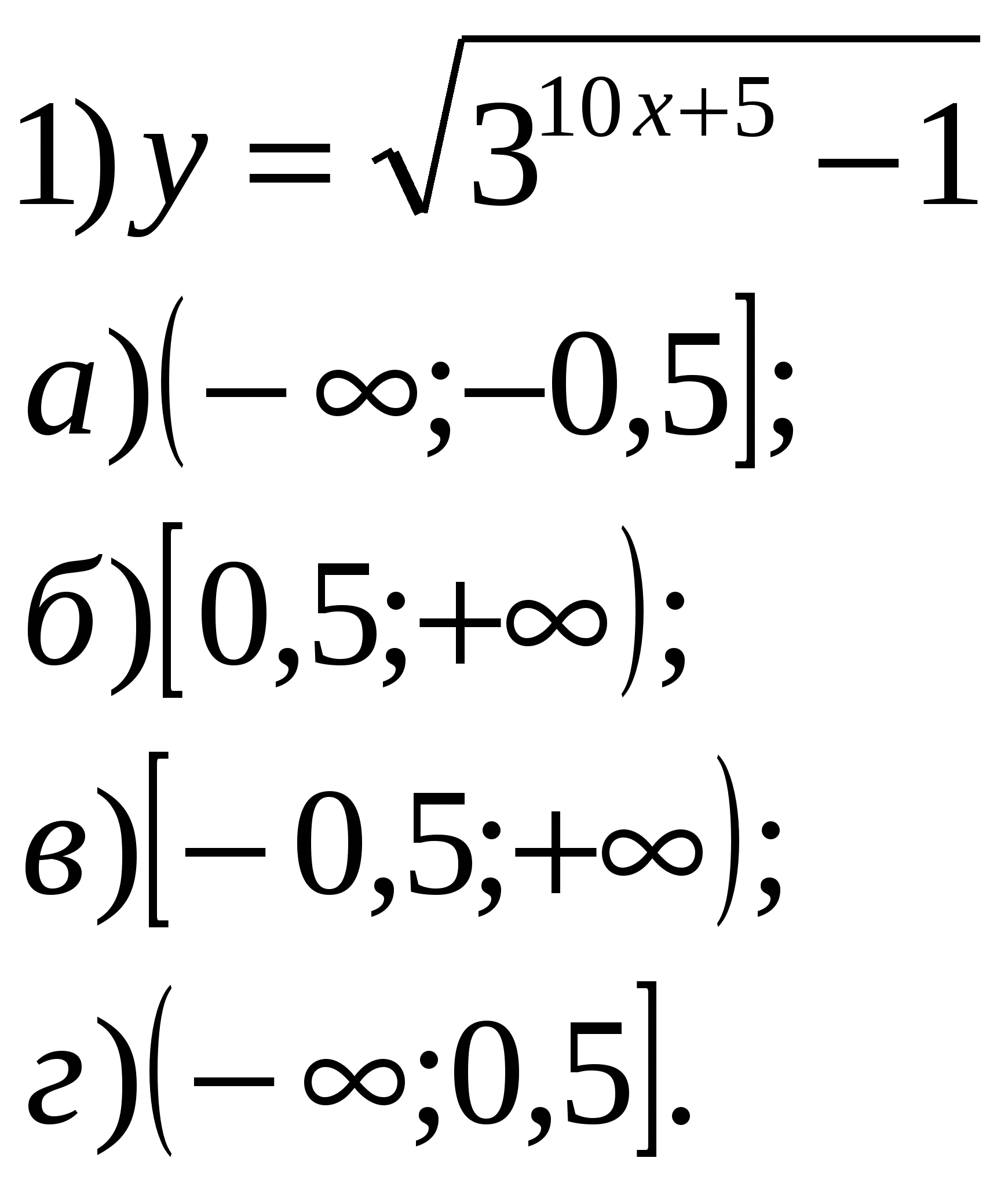





  1. Самостоятельная тестовая работа. Проводится самостоятельная тестовая работа по двум вариантам (на 7 минут)




Результаты своей работы учащиеся сдают учителю для дальнейшей проверки.


  1. Устная работа.

Учитель: Давайте рассмотрим несколько показательных уравнений, сводящихся к алгебраическим, и выполним следующее задание:
При помощи указанной замены переменной данное показательное уравнение привели к алгебраическому. Вставьте пропущенные коэффициенты.

1) 3*22х +4*2х – 5 = 0, t =2х; 3) 72х+2 + 3*7х+1= 53, t = 7 х;

t2 + t – 5 = 0. t2 + t – 53 = 0.
2) 3*5х+2 + 2*5х+1=77, t = 5х; 4) 3*36х + 4*6х+1 – 8 = 0, t = 6х;

t = 77. t2 + t – 8 = 0.
VII. Дифференцированная работа учащихся:

Пять учащихся садятся за ПК выполнять тесты, трое учащихся получают карточки для самостоятельной работы на местах, один учащийся получает карточку с заданием для решения у доски. С остальными учащимися работаем по учебнику, выполняем у доски № 261(3) и № 264(3).
Карточки для работы на местах:



Карточка № 1


№ 1. Укажите промежуток, которому принадлежит корень уравнения 3х+2+3х+1+3х=39.

А) [-2; 0]

Б) [2; 4]

В) (4; 9]

Г) (0; 2)
№ 2. Решить неравенство: 32x-1>272 .

А) (1,5; +&)

Б) (-&; 1,5)

В) (-&; 3,5)

Г) (3,5; +&)
№ 3. Решить уравнение:

Карточка № 2


№ 1. Укажите промежуток, которому принадлежит корень уравнения:

1) 37х+6=27. 2) 3х-½ * 3х+1 =1

А) (-4; -1) А) [-4; -2]

Б) (-1; 0) Б) (-2; -1)

В) (0; 1] В) [-1; 0)

Г) (1; 4) Г) (1; 2)

№ 2. Найдите область определения функции: .

А) [2/3; +)

Б) [1,5; +)

В) (-; 2/3]

Г) (2/3; +)


Карточка № 3





№ 1. Найдите сумму корней уравнения:

А) -2

Б) 0

В) 1

Г) 2
№ 2. Решите неравенство:

А) (-; -6]

Б) (-; -12]

В) [-6; +)

Г) (-; -1.5)
№ 3. Решите уравнение: 9х-3х-6=0

А) 1

Б) 3 и -2

В) -2

Г) 1/3



Карточка для работы у доски



Решить уравнение: 42|x|-3 – 3 . 4|x|-2 – 1=0.
Учитель: Скажите, пожалуйста, как можно решить систему уравнений

у – 3=|x – 2|,

y=2x-1 ?

После обсуждения у доски выполняется следующее задание:




Пусть (х0 ; у0) – решения системы у – 3=|x – 2| Найдите сумму х0 + у0.

y=2x-1 .


VIII. Устная работа.

1) Определите знак корня уравнения:

а) (1/5)х = 10;

б) 0,4х = 0,1;

в) 2,1х = 4;

г) 0,6х = 3.

2)Найдите ошибку в решении уравнения:




    1. Подведение итогов урока.

Учитель: Итак, что мы повторили с вами на сегодняшнем уроке?

Ученики отвечают на вопросы:

- повторили основные способы решения показательных уравнений и неравенств;

- рассмотрели примеры на каждый способ решения.
Выставление оценок за урок.


    1. Задание на дом: Стр. 86 «Проверь себя!»

- -